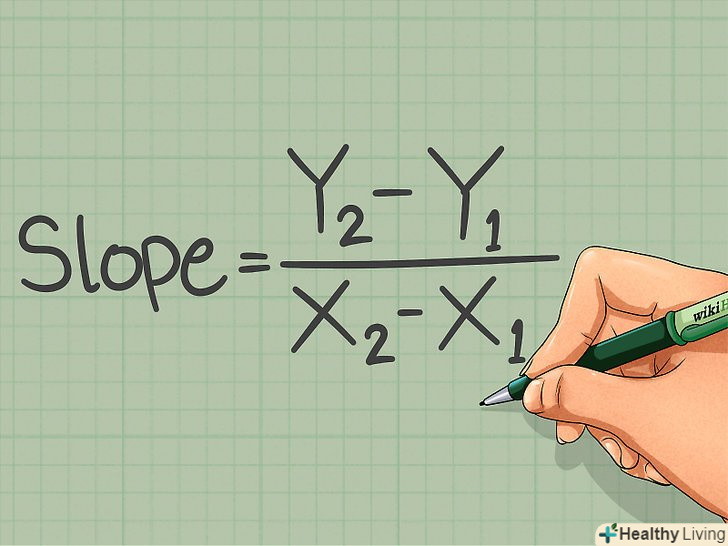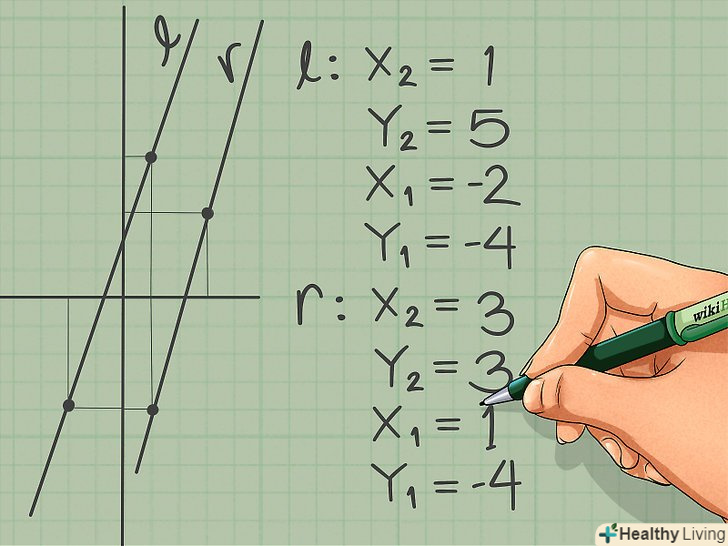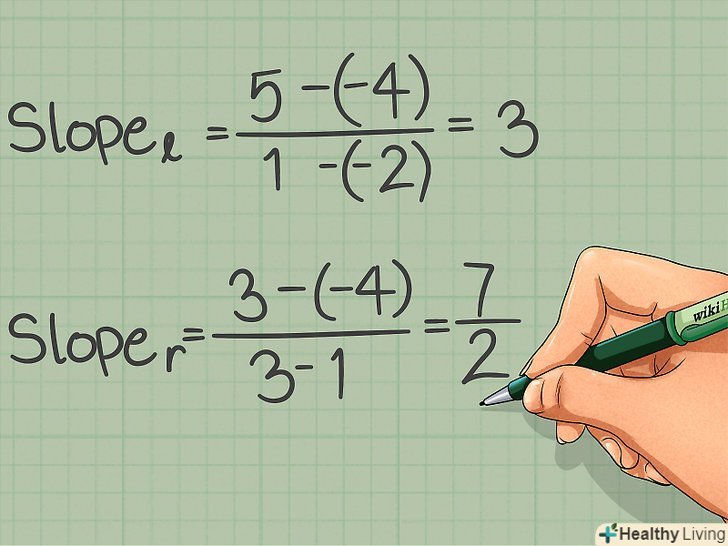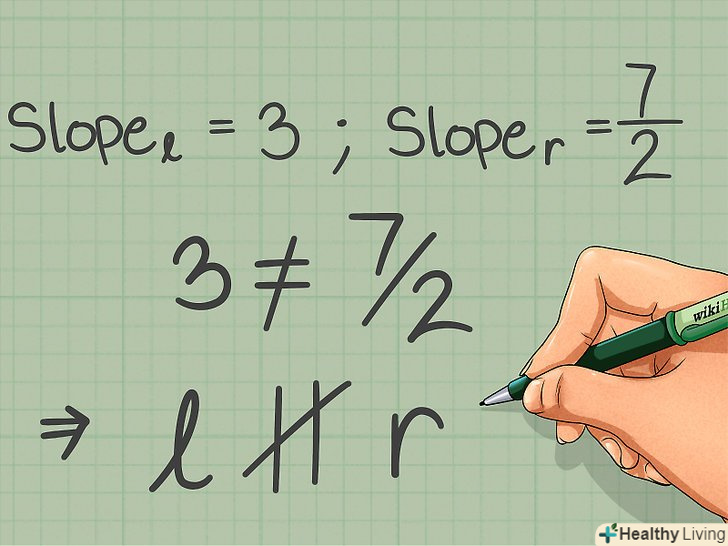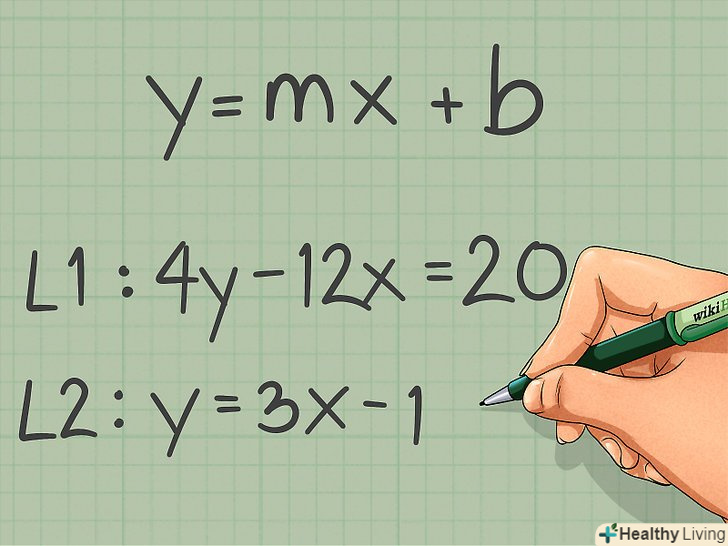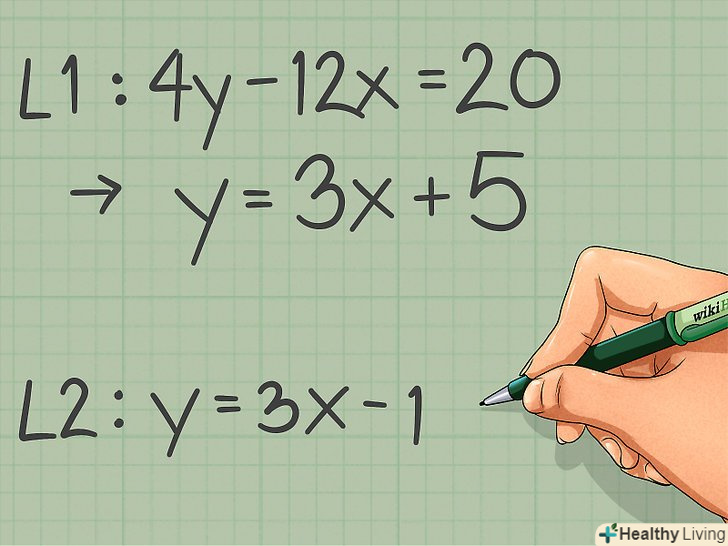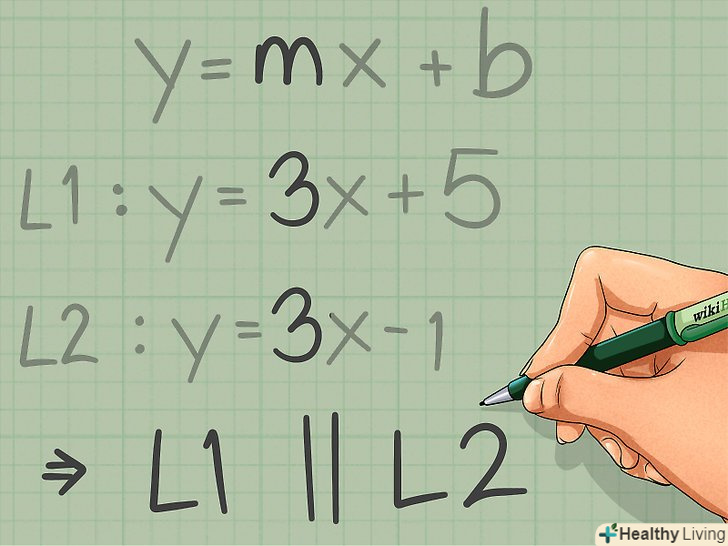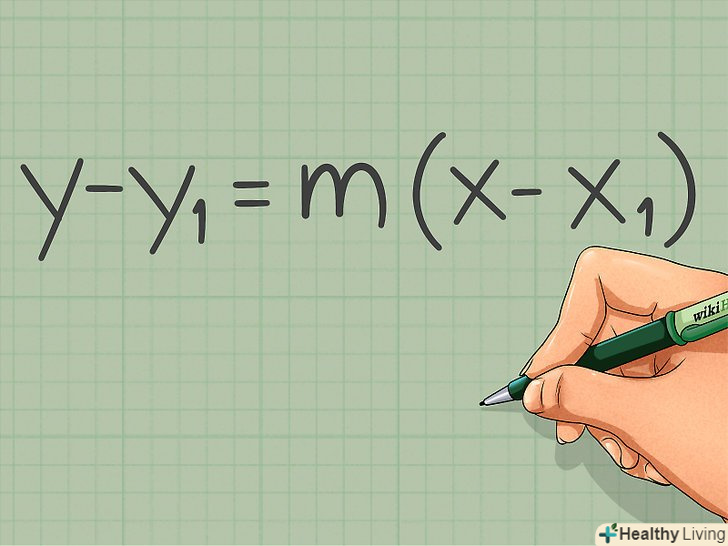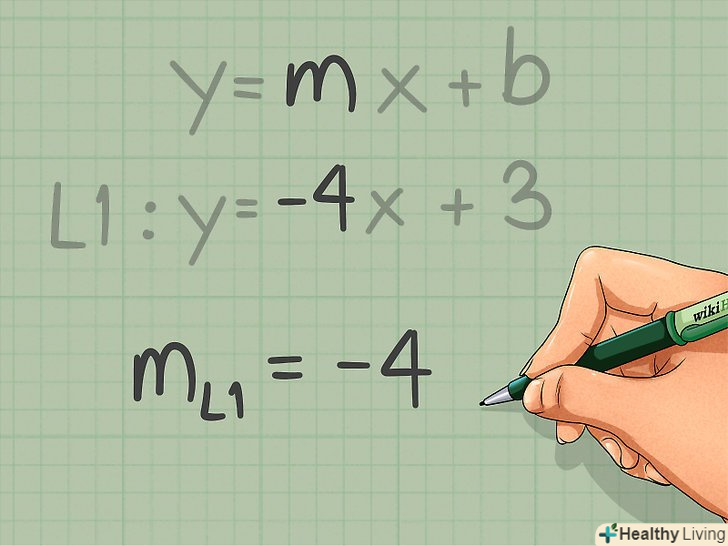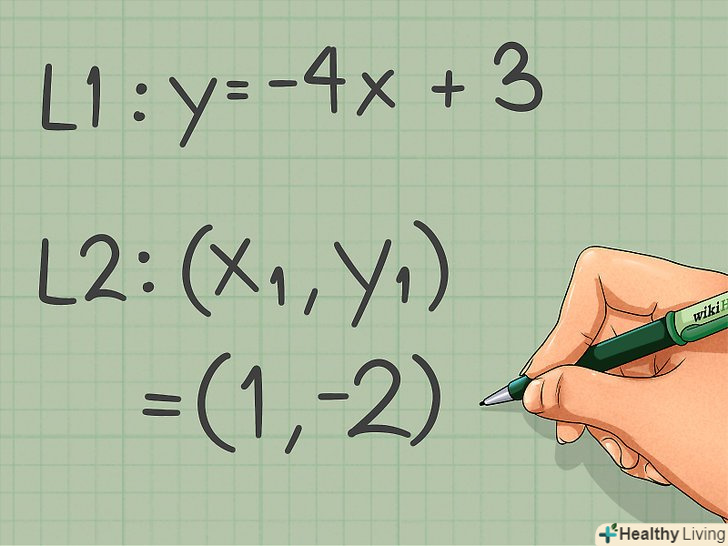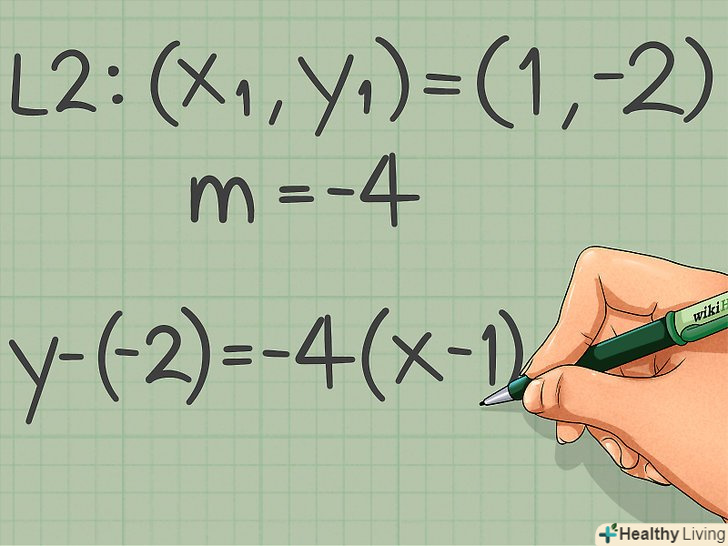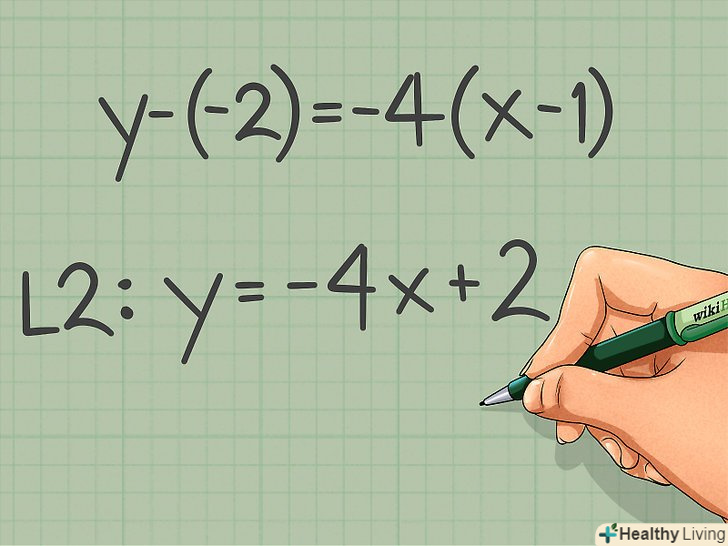1. Головна
    2. Геометрія
    3. Як визначити паралельність двох прямих-

Як визначити паралельність двох прямих-

Паралельними прямими називаються прямі, які лежать в одній площині і ніколи не перетинаються (протягом нескінченності).[1] у паралельних прямих однаковий кутовий коефіцієнт.[2] кутовий коефіцієнт дорівнює тангенсу кута нахилу прямої до осі абсцис, а саме відношенню зміни координати "y «до зміни координати»х".[3] часто паралельні прямі позначаються значком»ll". Наприклад, запис ABllCD означає, що пряма АВ паралельна прямий CD.

Метод1З 3:
Порівняння кутових коефіцієнтів двох прямих

  1. Запишіть формулу для обчислення кутового коефіцієнта. Формула: k = (y2 - y1)/(x2 - x1 ), де «x» і «y» – координати двох точок (будь-яких), що лежать на прямій. Координати першої точки, яка знаходиться ближче до початку координат, позначте як (x1, y1); координати другої точки, яка знаходиться далі від початку координат, позначте як (x2, y2).[4]
    • Наведену формулу можна сформулювати так: відношення вертикальної відстані (між двома точками) до горизонтальної відстані (між двома точками).
    • Якщо пряма зростає (спрямована вгору), її кутовий коефіцієнт позитивний.
    • Якщо пряма убуває (спрямована вниз), її кутовий коефіцієнт негативний.
  2. Визначте координати двох точок, які лежать на кожній прямій.координати точок записуються у вигляді (х, у), де «х» – координата по осі Х (осі абсцис), «y» – координата по осі «у» (вісь ординат). Щоб обчислити кутовий коефіцієнт, відзначте по дві точки на кожній прямій.[5]
    • Точки легко відзначити, якщо прямі намалювати на координатній площині.
    • Щоб визначити координати точки, проведіть від неї перпендикуляри (пунктиром) до кожної осі. Точка перетину пунктирної лінії з віссю Х - це координата "х«, а точка перетину з віссю Y – координата»у".
    • Наприклад: на прямій l лежать точки з координатами (1, 5) і (-2, 4), а на прямій r – точки з координатами (3, 3) і (1,-4).
  3. Підставте координати точок у формулу.потім відніміть відповідні координати і знайдіть відношення отриманих результатів. При підстановці координат в формулу не переплутайте їх порядок.
    • Обчислення кутового коефіцієнта прямої l: k = (5 - (-4))/(1 - (-2))
    • Віднімання: k = 9/3
    • Розподіл: k = 3
    • Обчислення кутового коефіцієнта прямої r: k = (3 - (-4))/(3 - 1) = 7/2
  4. Порівняйте кутові коефіцієнти.Пам'ятайте, що у паралельних прямих кутові коефіцієнти рівні. На малюнку прямі можуть здаватися паралельними, але якщо кутові коефіцієнта не рівні, такі прямі не паралельні один одному.[6]
    • У нашому прикладі 3 Не дорівнює 7/2, тому дані прямі не є паралельними.

Метод2 З 3:
За допомогою лінійного рівняння

  1. Запишіть лінійне рівняння.лінійне рівняння має вигляд y = kx + b, де k-кутовий коефіцієнт, b-координата "у «точки перетину прямої з віссю Y,» х «і» у" – змінні, що визначаються координатами точок, які лежать на прямій. За цією формулою можна з легкістю обчислити кутовий коефіцієнт k.[7]
    • Наприклад. Уявіть рівняння 4y-12x = 20 і у = 3x -1 у формі лінійного рівняння. Рівняння 4y-12x = 20 потрібно представити в необхідній формі, а ось рівняння у = 3x -1 вже записано як лінійне рівняння.
  2. Перепишіть рівняння у вигляді лінійного рівняння.іноді дається рівняння, яке не представлено у формі лінійного рівняння. Щоб переписати таке рівняння, потрібно виконати ряд нескладних математичних операцій.
    • Наприклад: перепишіть рівняння 4y - 12x = 20 у формі лінійного рівняння.
    • До обох сторін рівняння додайте 12x: 4y - 12x + 12x = 20 + 12x
    • Обидві сторони рівняння розділіть на 4, щоб відокремити «у»: 4y/4 = 12х/4 +20/4
    • Рівняння у вигляді лінійного: у = 3x + 5.
  3. Порівняйте кутові коефіцієнти.Пам'ятайте, що у паралельних прямих кутові коефіцієнти рівні. За допомогою рівняння y = kx + b, де k-кутовий коефіцієнт, можна знайти і порівняти кутові коефіцієнти двох прямих.
    • У нашому прикладі перша пряма описується рівнянням у = 3x + 5, тому кутовий коефіцієнт дорівнює 3. Друга пряма описується рівнянням у = 3x-1, тому кутовий коефіцієнт теж дорівнює 3. Так як кутові коефіцієнти рівні, дані прямі паралельні.
    • Зверніть увагу, що якщо у прямих з рівним кутовим коефіцієнтом коефіцієнт b (координата " у " точки перетину прямої з віссю Y) теж однаковий, такі прямі збігаються, а не є паралельними.[8]

Метод3 З 3:
Знаходження рівняння паралельної прямої

  1. Запишіть рівняння. наступне рівняння дозволить знайти рівняння паралельної (другої) прямої, якщо дано рівняння першої прямої і координати точки, яка лежить на шуканої паралельної( другої) прямої: y - y1= k (x-x1), де k – кутовий коефіцієнт, x1 і y1 – координати точки, що лежить на шуканої прямої, " х " і " у» – змінні, що визначаються координатами точок, які лежать на першій прямій.[9]
    • Наприклад: знайдіть рівняння прямої, яка паралельна прямій у = -4x + 3 і яка проходить через точку з координатами (1, -2).
  2. Визначте кутовий коефіцієнт даної (першої) прямої.щоб знайти рівняння паралельної (другої) прямої, спочатку потрібно визначити її кутовий коефіцієнт. Переконайтеся, що рівняння дано у формі лінійного рівняння, а потім знайдіть значення кутового коефіцієнта (k).
    • Друга пряма повинна бути паралельною даній прямій, яка описується рівнянням у = - 4x + 3. У цьому рівнянні k = -4, тому у другій прямій буде такий же кутовий коефіцієнт.
  3. У представлене рівняння підставте координати точки, яка лежить на другій прямій.цей метод застосуємо тільки в тому випадку, якщо дані координати точки, що лежить на другій прямій, рівняння якої потрібно знайти. Не переплутайте координати такої точки з координатами точки, яка лежить на даній (першої) прямій. Пам'ятайте, що якщо у прямих з рівним кутовим коефіцієнтом коефіцієнт b (координата " у " точки перетину прямої з віссю Y) теж однаковий, такі прямі збігаються, а не є паралельними.
    • У нашому прикладі точка, що лежить на другій прямій, має координати (1, -2).
  4. Запишіть рівняння другої прямої. для цього відомі значення підставте в рівняння y – y1= k(x – x1). Підставте знайдений кутовий коефіцієнт і координати точки, що лежить на другій прямій.
    • У нашому прикладі k = -4, а координати точки (1, -2): у - (-2) = -4 (х - 1)
  5. Спростіть рівняння.Спростіть рівняння і запишіть його у вигляді лінійного рівняння. Якщо намалювати другу пряму на координатній площині, вона буде паралельна даної (першої) прямий.
    • Наприклад: у - (-2) = -4 (х - 1)
    • Два "мінуса" дають "плюс": у + 2 = -4 (х -1)
    • Розкрийте дужки: у + 2 = -4x + 4.
    • З обох сторін рівняння відніміть -2: у + 2 - 2 = -4x + 4 - 2
    • Спрощене рівняння: у = - 4x + 2

Джерела

  1. ↑ Https://www.mathsisfun.com/perpendicular-parallel.html
  2. ↑ Https://www.mathsisfun.com/algebra/line-parallel-perpendicular.html
  3. ↑ Https://www.mathsisfun.com/geometry/slope.html
  4. ↑ Http://www.mathopenref.com/coordslope.html
  5. ↑ Http://www.mathopenref.com/coordparallel.html
  6. ↑ Http://www.mathopenref.com/coordparallel.html
  7. ↑ Http://www.mathopenref.com/coordequation.html
  8. ↑ Https://www.mathsisfun.com/algebra/line-parallel-perpendicular.html
  9. ↑ Http://www.mathopenref.com/coordequationps.html

Ще почитати: