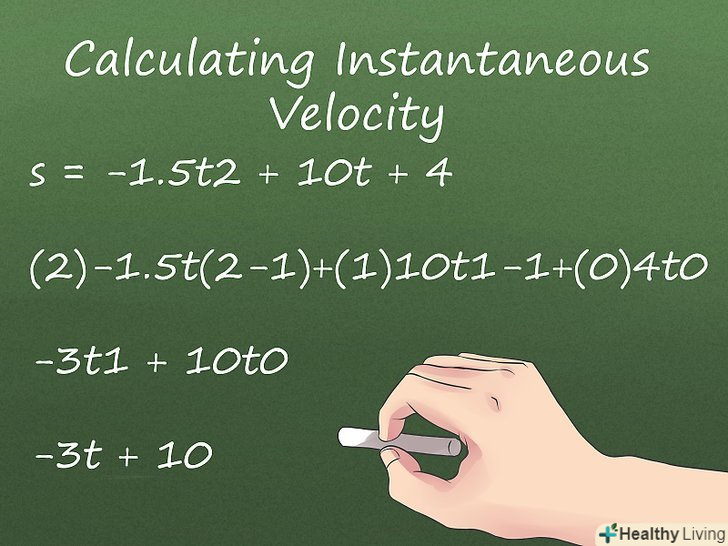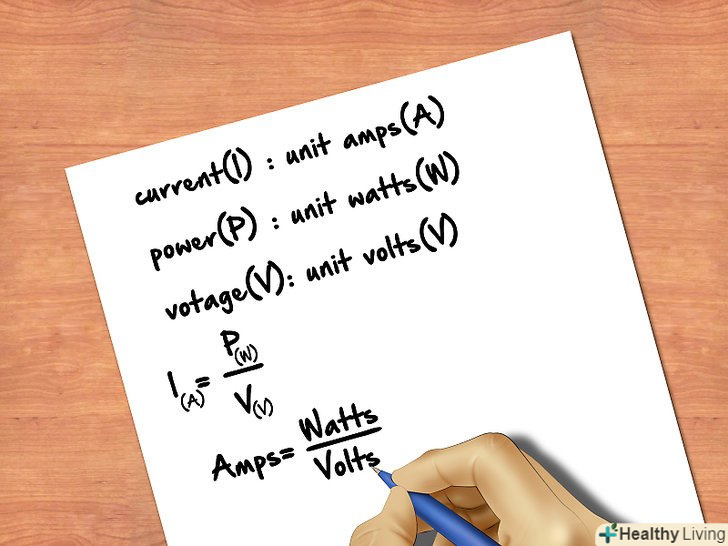1. Головна
    2. Фізика
    3. Як обчислити миттєву швидкість: 11 кроків

Як обчислити миттєву швидкість: 11 кроків

Швидкість - це швидкість переміщення об'єкта в заданому напрямку. [1] в загальних цілях знаходження швидкості об'єкта (v) — просте завдання: потрібно розділити переміщення (s) протягом певного часу (s) на цей час (t), тобто скористатися формулою v = s/t. однак таким способом отримують середню швидкість тіла. Використовуючи деякі обчислення, можна знайти швидкість тіла в будь-якій точці шляху. Така швидкість називається Миттєвою швидкістю і обчислюється за формулою V = (ds)/(dt) , тобто являє собою похідну від формули для обчислення середньої швидкості тіла. [2]

Частина1З 3:
Обчислення миттєвої швидкості

  1. Почніть з рівняння. для обчислення миттєвої швидкості необхідно знати рівняння, що описує переміщення тіла (його позицію в певний момент часу), [3] тобто таке рівняння, на одній стороні якого знаходиться s (переміщення тіла), а на іншій стороні — члени зі змінною t (час). [4] наприклад:

    S = -1.5t 2 + 10t + 4

    • У цьому рівнянні:
      Переміщення = s . Переміщення-пройдений об'єктом шлях. Наприклад, якщо тіло перемістилося на 10 м вперед і на 7 м назад, то загальне переміщення тіла дорівнює 10-7 = 3 м (а на 10 + 7 = 17 м).
      Час = t . Зазвичай вимірюється в секундах.
  2. Обчисліть похідну рівняння. щоб знайти миттєву швидкість тіла, чиї переміщення описуються наведеним вище рівнянням, потрібно обчислити похідну цього рівняння. Похідна-це рівняння, що дозволяє обчислити нахил графіка в будь-якій точці (в будь-який момент часу). Щоб знайти похідну, продифференцируйте функцію наступним чином: Якщо y = a * x n , то похідна = a * n * x n-1 . Це правило застосовується до кожного члена многочлена.
    • Іншими словами, похідна кожного члена зі змінною t дорівнює добутку множника (що стоїть перед змінною) і ступеня змінної, помноженому на змінну в ступені, рівну вихідної ступеня мінус 1. Вільний член (член без змінної, тобто число) зникає, тому що множиться на 0. У нашому прикладі:

      S = -1.5t 2 + 10t + 4
      (2)-1.5t (2-1) + (1)10t 1 - 1 + (0)4t 0
      -3t 1 + 10t 0
      -3t + 10

  3. Замініть " s " На "ds / dt", щоб показати, що нове рівняння — це похідна від вихідного рівняння (тобто похідна S від t). похідна-це нахил графіка в певній точці (в певний момент часу). Наприклад, щоб знайти нахил лінії, описуваної функцією s = -1.5 t 2 + 10T + 4 при t = 5, просто підставте 5 в рівняння похідної.
    • У нашому прикладі рівняння похідної має виглядати наступним чином:

      Ds/dt = -3t + 10

  4. У рівняння похідної підставте відповідне значення t, щоб знайти миттєву швидкість в певний момент часу. [5] наприклад, якщо ви хочете знайти миттєву швидкість при t = 5, просто підставте 5 (замість t) в рівняння похідної ds/dt = -3 + 10. Потім вирішіть рівняння:

    Ds/dt = -3t + 10
    ds/dt = -3(5) + 10
    ds/dt = -15 + 10 = -5 м / с

    • Зверніть увагу на одиницю виміру миттєвої швидкості: м/с.Так як нам дано значення переміщення в метрах, а час — в секундах, і швидкість дорівнює відношенню переміщення до часу, то одиниця виміру м/с — правильна.

Частина2З 3:
Графічна оцінка миттєвої швидкості

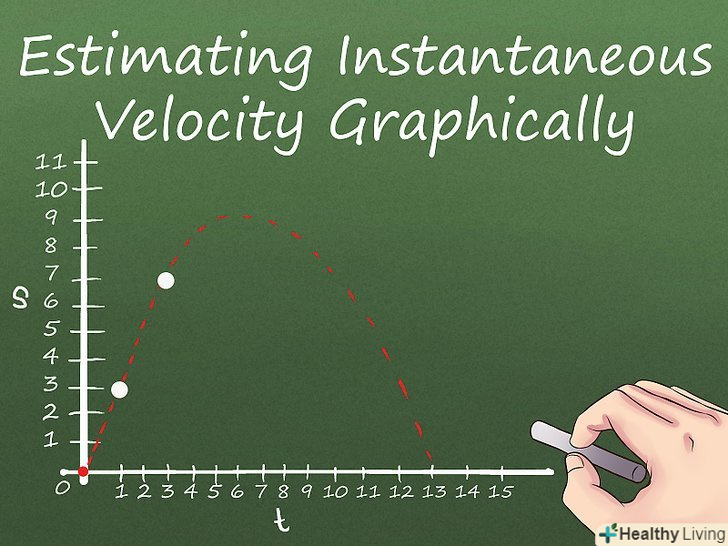
  1. Побудуйте графік переміщення тіла. у попередньому розділі ви обчислювали миттєву швидкість за формулою (рівняння похідної, що дозволяє знайти нахил графіка в певній точці). [6] побудувавши графік переміщення тіла, ви можете знайти його нахил в будь-якій точці, а отже визначити миттєву швидкість в певний момент часу .
    • По осі Y відкладайте переміщення, а по осі X — час. Координати точок (x,у) отримаєте через підстановку різних значень t в вихідне рівняння переміщення і обчислення відповідних значень s.
    • Графік може опускатися нижче осі X. Якщо графік переміщення тіла опускається нижче осі X, то це означає, що тіло рухається в зворотному напрямку від точки початку руху. Як правило, графік не поширюється за вісь Y — негативні значення x) - ми не вимірюємо швидкості об'єктів, що рухаються назад у часі!
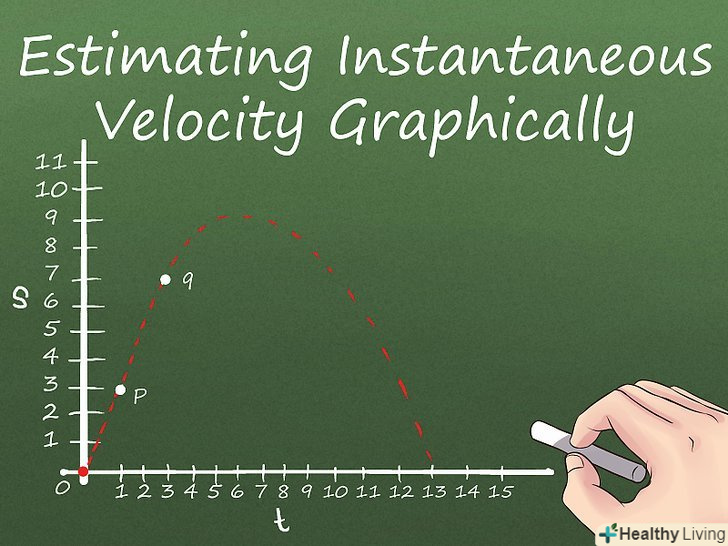
  2. Виберіть на графіку (кривої) точку P і близьку до неї точку Q. щоб знайти нахил графіка в точці P, використовуємо поняття межі. Межа-стан, при якому величина січної, проведеної через 2 точки P і Q, що лежать на кривій, прагне до нуля.
    • Наприклад, розглянемо точкиP(1,3) і Q(4,7) і обчислимо миттєву швидкість в точці P.
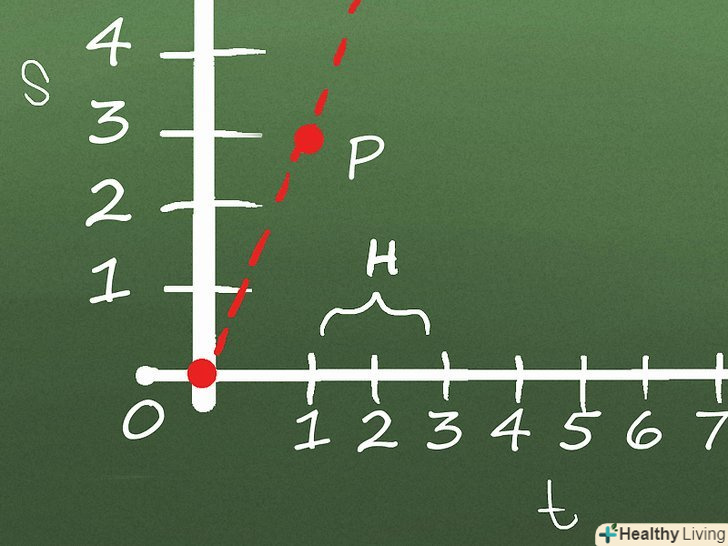
  3. Знайдіть нахил відрізка PQ. нахил відрізка PQ дорівнює відношенню різниці значень координат " у "точок P і Q до різниці значень координат" х " точок P і Q. іншими словами, H = (y Q - y P )/(x Q - x P ) , де H — нахил відрізка PQ. У нашому прикладі нахил відрізка PQ дорівнює:

    H = (y Q - y P )/(x Q - x P )
    H = (7 - 3)/(4 - 1)
    H = (4)/(3) = 1.33

  4. Повторіть процес кілька разів, наближаючи точку Q до точки P. чим менше відстань між двома точками, тим ближче значення нахилу отриманих відрізків до нахилу графіка в точці P. у нашому прикладі виконаємо обчислення для точки Q з координатами (2,4.8), (1.5,3.95) і (1.25, 3.49) (координати точки P залишаються колишніми):

    Q = (2,4.8): H = (4.8 - 3)/(2 - 1)
    H = (1.8)/(1) = 1.8

    Q = (1.5,3.95): H = (3.95 - 3)/(1.5 - 1)
    H = (.95)/(.5) = 1.9

    Q = (1.25,3.49): H = (3.49 - 3)/(1.25 - 1)
    H = (.49)/(.25) = 1.96

  5. Чим менше відстань між точками P і Q, тим ближче значення H до нахилу графіка в точці P при гранично малій відстані між точками P і Q, значення H дорівнюватиме нахилу графіка в точці P Так як ми не можемо виміряти або обчислити гранично малу відстань між двома точками, графічний спосіб дає оціночне значення нахилу графіка в точці Р.
    • У нашому прикладі при наближенні Q до P ми отримали наступні значення h: 1.8; 1.9 і 1.96. Так як ці числа прагнуть до 2, то можна сказати, що нахил графіка в точці P дорівнює2 .
    • Пам'ятайте, що нахил графіка в даній точці дорівнює похідної функції (по якій побудований цей графік) в цій точці. Графік відображає переміщення тіла з плином часу і, як зазначалося в попередньому розділі, миттєва швидкість тіла дорівнює похідній від рівняння переміщення цього тіла. Таким чином, можна заявити, що при t = 2 миттєва швидкість дорівнює2 м / с (це оціночне значення).

Частина3З 3:
Приклади

  1. Обчисліть миттєву швидкість при t = 4, Якщо переміщення тіла описується рівнянням s = 5T 3 - 3t 2 + 2t + 9. цей приклад схожий на задачу з першого розділу з тією лише різницею, що тут дано рівняння третього порядку (а не другого).
    • Спочатку обчислимо похідну цього рівняння:

      S = 5t 3 - 3t 2 + 2t + 9
      s = (3)5t (3 - 1) - (2)3t (2 - 1) + (1)2t (1 - 1) + (0)9t 0 - 1
      15t (2) - 6t (1) + 2t (0)
      15t (2) - 6t + 2

    • Тепер підставимо в рівняння похідної значення t = 4:

      S = 15t (2) - 6t + 2
      15(4) (2) - 6(4) + 2
      15(16) - 6(4) + 2
      240 - 24 + 2 = 22 м / с

  2. Оцінимо значення миттєвої швидкості в точці з координатами (1,3) на графіку функції s = 4T 2 - t. у цьому випадку точка P має координати (1,3) і необхідно знайти кілька координат точки Q, Що лежить близько до точки P. потім обчислимо H і знайдемо оціночні значення миттєвої швидкості.
    • Спочатку знайдемо координати Q при t = 2, 1.5, 1.1 і 1.01.

      S = 4t 2 - t

      T = 2: s = 4(2) 2 - (2)
      4(4) - 2 = 16 - 2 = 14, so Q = (2,14)

      T = 1.5: s = 4(1.5) 2 - (1.5)
      4(2.25) - 1.5 = 9 - 1.5 = 7.5, so Q = (1.5,7.5)

      T = 1.1: s = 4(1.1) 2 - (1.1)
      4(1.21) - 1.1 = 4.84 - 1.1 = 3.74, so Q = (1.1,3.74)

      T = 1.01: s = 4(1.01) 2 - (1.01)
      4(1.0201) - 1.01 = 4.0804 - 1.01 = 3.0704, so Q = (1.01,3.0704)

    • Тепер обчислимо H:

      Q = (2,14): H = (14 - 3)/(2 - 1)
      H = (11)/(1) = 11

      Q = (1.5,7.5): H = (7.5 - 3)/(1.5 - 1)
      H = (4.5)/(.5) = 9

      Q = (1.1,3.74): H = (3.74 - 3)/(1.1 - 1)
      H = (.74)/(.1) = 7.3

      Q = (1.01,3.0704): H = (3.0704 - 3)/(1.01 - 1)
      H = (.0704)/(.01) = 7.04

    • Так як отримані значення H прагнуть до 7, то можна сказати, що миттєва швидкість тіла в точці (1,3) дорівнює7 м / с (оціночне значення).

Поради

  • Щоб знайти прискорення (зміна швидкості з плином часу), використовуйте метод з першої частини, щоб отримати похідну функції переміщення. Потім візьміть ще раз похідну від отриманої похідної. Це дасть вам рівняння для знаходження прискорення в даний момент часу-все, що вам потрібно зробити, це підставити значення для часу.
  • Рівняння, що описує залежність у (переміщення) від x (час), може бути дуже простим, наприклад: у = 6x + 3. В цьому випадку нахил є постійним і не треба брати похідну, щоб його знайти. Відповідно до теорії лінійних графіків, їх нахил дорівнює коефіцієнту при змінній x, тобто в нашому прикладі =6.
  • Переміщення подібно відстані, але воно має певний напрямок, що робить його векторної величиною. Переміщення може бути негативним, в той час як відстань буде тільки позитивним.

Джерела

  1. ↑ Http://www.physicsclassroom.com/class/1dkin/u1l1d.cfm
  2. ↑ Http://formulas.tutorvista.com/physics/instantaneous-velocity-formula.html
  3. ↑ Http://spiff.rit.edu/classes/phys211/lectures/disvel/disvel_all.html
  4. ↑ Https://www.khanacademy.org/science/physics/one-dimensional-motion/displacement-velocity-time/a/what-is-displacement
  5. ↑ Https://sciencestruck.com/instantaneous-velocity
  6. ↑ Https://www.mathopenref.com/calcinstantvel.html

Ще почитати: