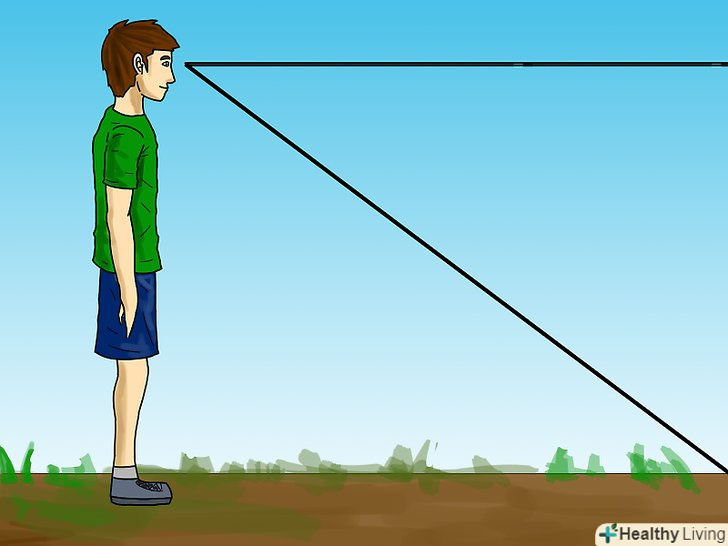
Ви коли-небудь спостерігали Захід Сонця і задавалися питанням про відстань від вас до горизонту? Якщо ви можете визначити висоту ваших очей над рівнем моря, ви можете обчислити відстань від вас до горизонту способами, описаними в цій статті.
Кроки
Метод1З 3:
Обчислення відстані за допомогою геометрії
Метод1З 3:
 Виміряйте "висоту очей". виміряйте висоту від землі до ваших очей. Один із способів зробити це-виміряти відстань між очима і верхньою частиною голови. Відніміть це значення з вашого зростання і ви отримаєте висоту від поверхні Землі до ваших очей. Якщо ви стоїте на рівні моря, то це єдиний вимір, який потрібно провести.
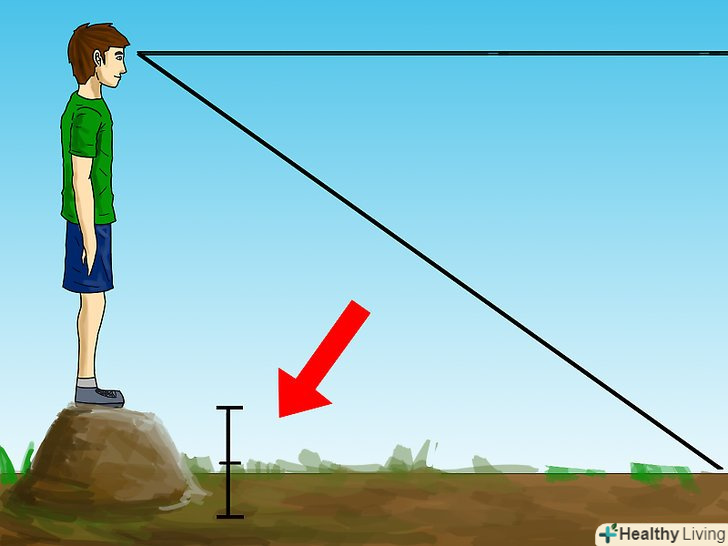
Виміряйте "висоту очей". виміряйте висоту від землі до ваших очей. Один із способів зробити це-виміряти відстань між очима і верхньою частиною голови. Відніміть це значення з вашого зростання і ви отримаєте висоту від поверхні Землі до ваших очей. Якщо ви стоїте на рівні моря, то це єдиний вимір, який потрібно провести. Додайте висоту височини, якщо ви стоїте, наприклад, на пагорбі або на даху будівлі. додайте висоту висоти до висоти від землі до ваших очей (використовуйте метри як одиницю виміру).
Додайте висоту височини, якщо ви стоїте, наприклад, на пагорбі або на даху будівлі. додайте висоту висоти до висоти від землі до ваших очей (використовуйте метри як одиницю виміру). Помножте отримане значення на 13 м.
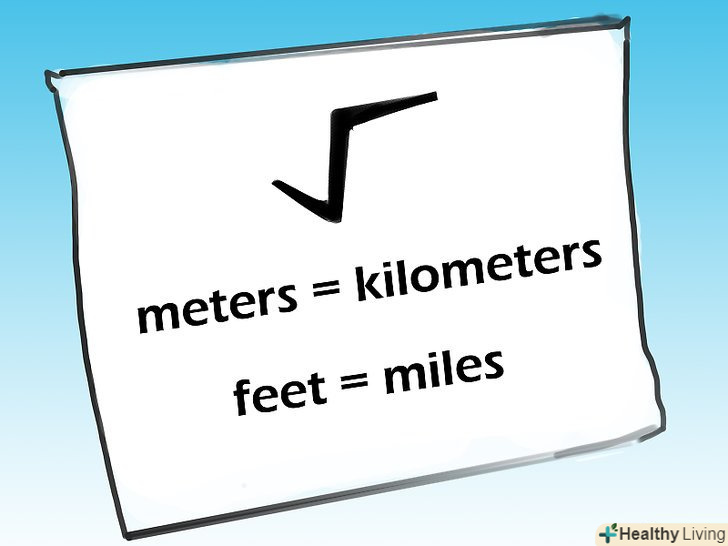
Помножте отримане значення на 13 м. Витягніть квадратний корінь і ви отримаєте відстань до горизонту (в кілометрах). обчислена відстань являє собою пряму лінію від ваших очей до горизонту.
Витягніть квадратний корінь і ви отримаєте відстань до горизонту (в кілометрах). обчислена відстань являє собою пряму лінію від ваших очей до горизонту.- Фактична відстань до горизонту (при подорожі по поверхні Землі) буде більше через кривизну поверхні. Перейдіть до наступного розділу для більш точного обчислення відстані до горизонту.
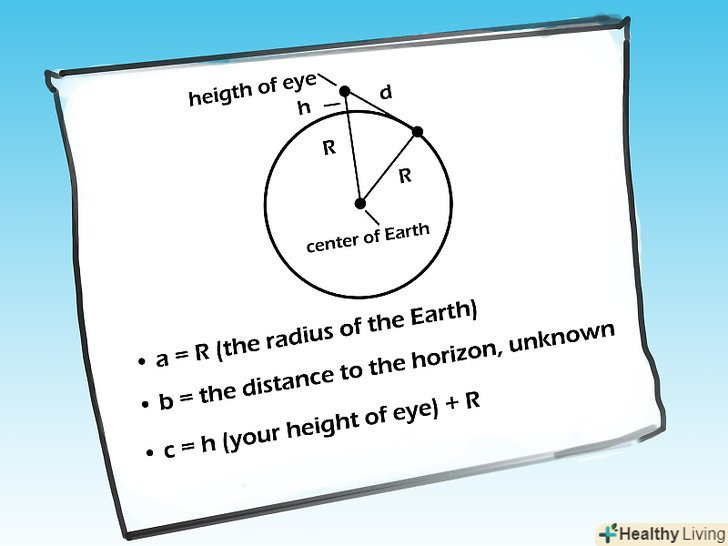
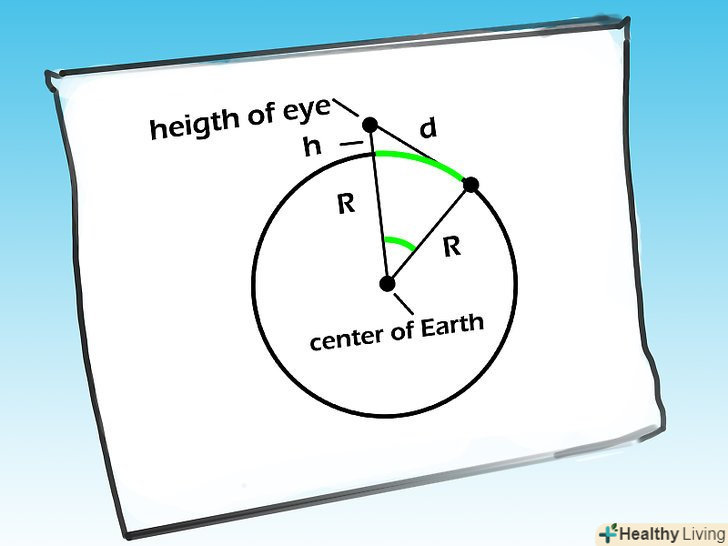
 Усвідомте суть цього методу. в його основі трикутник з наступними вершинами: точка спостереження (ваші очі), точка на горизонті (на яку ви дивитеся) і центр Землі.
Усвідомте суть цього методу. в його основі трикутник з наступними вершинами: точка спостереження (ваші очі), точка на горизонті (на яку ви дивитеся) і центр Землі.- Знаючи радіус Землі і вимірюючи висоту від землі до ваших очей (плюс висота височини, якщо необхідно), невідомим залишається тільки відстань між точкою спостереження і точкою на горизонті. Так як трикутник є прямокутним, то в обчисленнях можна використовувати теорему Піфагора: a 2
+ b
2
= c
2
, де:
• a = R (радіус Землі)
• b = відома відстань до горизонту
• c = h (висота від землі до ваших очей) + R (радіус Землі).
- Знаючи радіус Землі і вимірюючи висоту від землі до ваших очей (плюс висота височини, якщо необхідно), невідомим залишається тільки відстань між точкою спостереження і точкою на горизонті. Так як трикутник є прямокутним, то в обчисленнях можна використовувати теорему Піфагора: a 2
+ b
2
= c
2
, де:
Метод2З 3:
Обчислення відстані за допомогою тригонометрії
Метод2З 3:
 Обчисліть відстань, яку потрібно пройти (або проїхати) до горизонту, використовуючи наступну формулу:
Обчисліть відстань, яку потрібно пройти (або проїхати) до горизонту, використовуючи наступну формулу:- D = r * arccos(R/(R + h)), де
• d = відстань до горизонту
• R = радіус Землі
• h = висота від землі до ваших очей
- D = r * arccos(R/(R + h)), де
 Збільште R на 20%, щоб компенсувати спотворення від заломлення світлових променів і отримати більш точний результат. геометричний горизонт не те ж саме, що оптичний горизонт, який бачать очі. Чому це так?
Збільште R на 20%, щоб компенсувати спотворення від заломлення світлових променів і отримати більш точний результат. геометричний горизонт не те ж саме, що оптичний горизонт, який бачать очі. Чому це так?- Атмосфера заломлює світлові промені, які поширюються по прямій. Це означає, що промінь світла певним чином повторює кривизну Землі; тому оптичний горизонт знаходиться трохи далі, ніж геометричний горизонт.
- На жаль, ступінь заломлення променів не є постійною або прогнозованою величиною, так як вона залежить від зміни температури зі зміною висоти над поверхнею Землі. Тому застосовують "усереднену" поправку: радіус Землі збільшують на 20%.
 Усвідомте суть цього розрахунку. він обчислює довжину дуги, яка з'єднує ваші ноги з істинним горизонтом (на малюнку показана зеленим кольором). агссоѕ(R/(R+h)) обчислює кут, який утворений двома відрізками: від центру Землі до істинного горизонту і від центру Землі до точки, де ви стоїте. Потім цей кут ми множимо на R, щоб отримати довжину дуги, яка і є шукане відстань.
Усвідомте суть цього розрахунку. він обчислює довжину дуги, яка з'єднує ваші ноги з істинним горизонтом (на малюнку показана зеленим кольором). агссоѕ(R/(R+h)) обчислює кут, який утворений двома відрізками: від центру Землі до істинного горизонту і від центру Землі до точки, де ви стоїте. Потім цей кут ми множимо на R, щоб отримати довжину дуги, яка і є шукане відстань.
Метод3З 3:
Альтернативний Геометричний розрахунок
Метод3З 3:
 Уявіть поверхню океану. цей метод застосовується при вимірах, виконаних виключно в футах і милях.
Уявіть поверхню океану. цей метод застосовується при вимірах, виконаних виключно в футах і милях. Обчисліть відстань в милях, підставивши в наступну формулу висоту h (в футах) від землі до ваших очей: d = 1.2246 * квадратний корінь (h)
Обчисліть відстань в милях, підставивши в наступну формулу висоту h (в футах) від землі до ваших очей: d = 1.2246 * квадратний корінь (h) Виведіть формулу з теореми Піфагора. (R + h) 2 = R 2 + d 2 . Знаходимо d (припускаючи, що R&#gt;&#gt;h і радіус Землі дорівнює 3959 милям):d = SQRT (2 * R * h)
Виведіть формулу з теореми Піфагора. (R + h) 2 = R 2 + d 2 . Знаходимо d (припускаючи, що R&#gt;&#gt;h і радіус Землі дорівнює 3959 милям):d = SQRT (2 * R * h)
Поради
- Ці розрахунки використовуються для отримання відстані до істинного горизонту або до точки дотику неба і землі (за умови, що на шляху до горизонту немає ніяких перешкод, наприклад, в океані). Однак на поверхні Землі зустрічаються гори або будівлі; в цьому випадку ці розрахунки все одно дадуть відстань до істинного горизонту, але вам доведеться пройти/проїхати більшу відстань через перешкоди на вашому шляху.