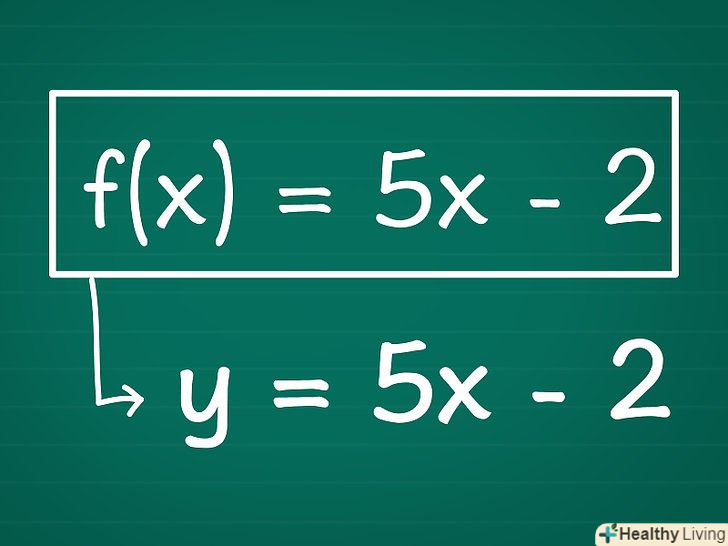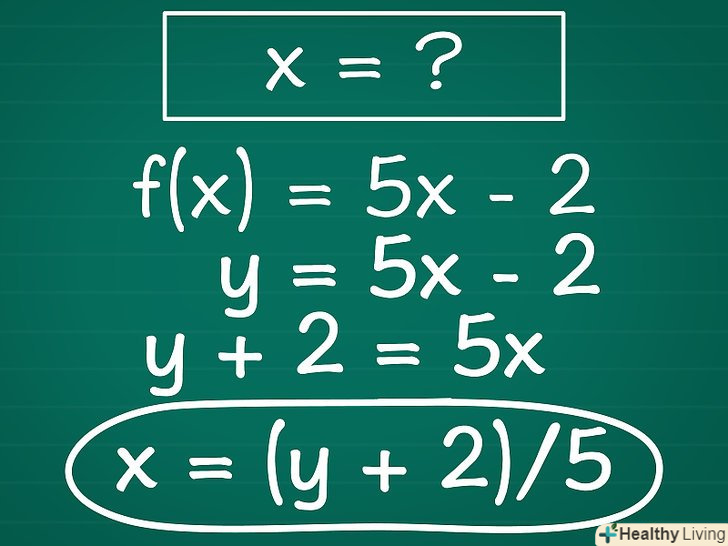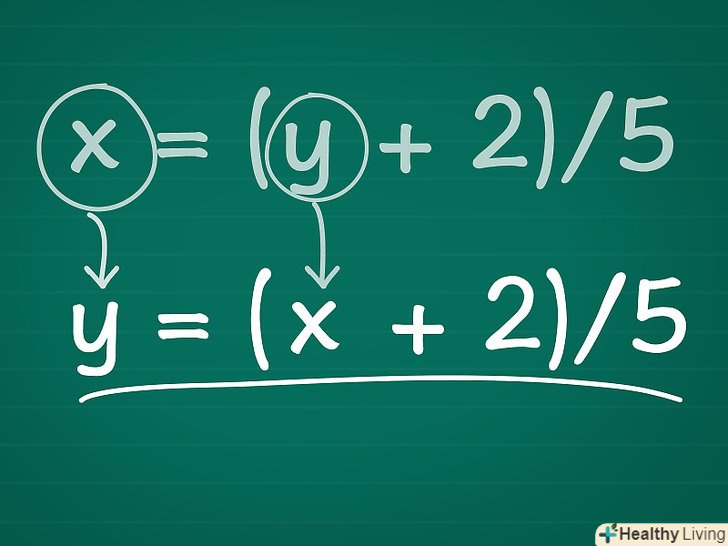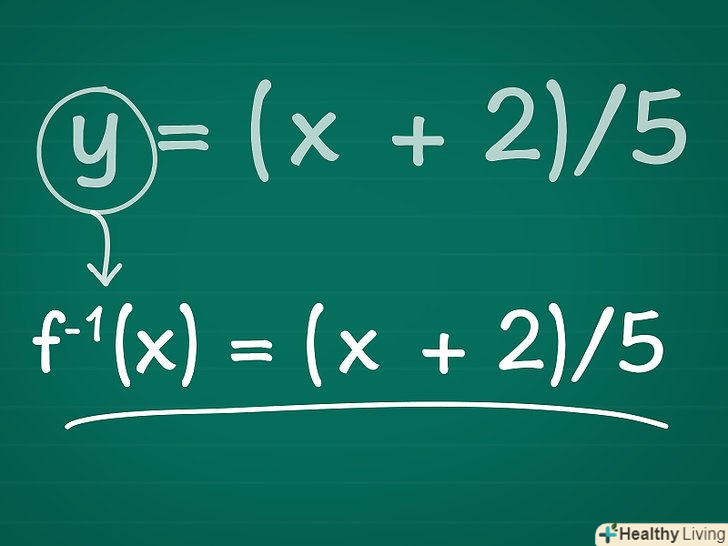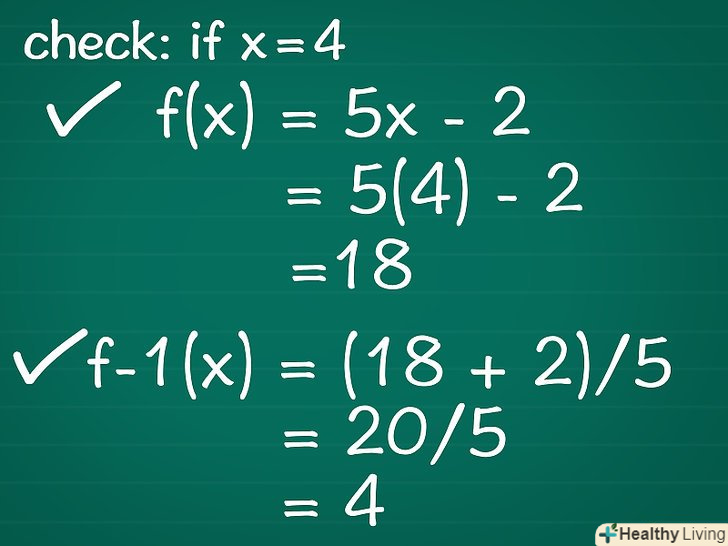Математичні функції, які зазвичай позначаються як f(x) або g(x), можна представити як порядок виконання математичних операцій, які дозволяють прийти від «x» до «y». Зворотна функція f(x) записується як f-1(x).[1] у разі простих функцій знайти зворотну функцію нескладно.
Кроки
Повністю перепишіть функцію, замінивши f (x) на y. При цьому «у» повинна знаходитися на одній стороні функції, а «x» — на іншій. Якщо вам дана функція виду 2 + y = 3x2, вам необхідно ізолювати «у» на одній стороні, а «x» — на іншій.- Приклад. Перепишемо цю функцію f (x) = 5x - 2 ЯкY = 5x - 2. f (x) і» y " взаємозамінні.
- F (x) - це стандартний запис функції, але якщо ви маєте справу з декількома функціями, то кожній з них потрібно буде привласнити свою букву, щоб їх було легше відрізняти один від одного. Наприклад, часто функції позначають як g (x) і h(x).
-
Знайдіть "x".іншими словами, виконайте математичні операції, необхідні для ізолювання " x " по одну сторону від знака рівності. Основні алгебраїчні принципи: якщо «x» має числовий коефіцієнт, то розділіть обидві сторони функції на цей коефіцієнт; якщо до члена з «x» додається деякий вільний член, відніміть його з обох сторін функції (і так далі).
- Пам'ятайте, що ви можете застосовувати будь-яку операцію по відношенню до однієї зі сторін рівняння тільки в тому випадку, якщо ви застосовуєте ту ж операцію по відношенню до всіх членів по обидві сторони від знака рівності.[2]
- У нашому прикладі додайте 2 до обох частин рівняння. Ви отримаєте y + 2 = 5x. потім розділіть обидві частини рівняння на 5 і отримаєте (y + 2)/5 = x. і, нарешті, перепишіть рівняння з «x» в лівій частині:X = (y + 2)/5.
-
Поміняйте змінні, замінивши " x " на " y " і навпаки.Результатом буде функція, зворотна вихідної. Іншими словами, якщо ми підставимо значення «x» в початкове рівняння і знайдемо значення «у», то, підставивши це значення «у» в зворотну функцію, ми отримаємо значення «x».
- У нашому прикладі отримаємоY = (x + 2)/5.
-
Замініть» у " на f-1(x).зворотні функції зазвичай записують у вигляді f-1(x) = (члени з «x»). Слід зазначити, що в даному випадку -1 — це не показник ступеня; це просто позначення зворотної функції.
- Так як «x» в -1 ступеня дорівнює 1/x, то f-1(x) — це форма запису 1/f(x), що також позначає функцію, зворотну f(x).
-
Перевірте роботу, замість» x " підставивши постійне значення в вихідну функцію.якщо ви правильно знайшли зворотну функцію, підставивши в неї значення "у«, ви знайдете підставлене значення»x".
- Наприклад, підставте x = 4. Ви отримаєте f(x) = 5(4) - 2 або f (x) = 18.
- Тепер підставте 18 в зворотну функцію і отримаєте y = (18 + 2)/5 = 20/5 = 4. Тобто у = 4. Це підставлене значення "x", тому ви правильно знайшли зворотну функцію.
Поради
- Коли ви виконуєте алгебраїчні операції над функціями, ви можете вільно замінювати f(x) = y і f^(-1) (x) = y в обох напрямках. Але прямий запис зворотної функції може призвести до плутанини, тому дотримуйтесь запису f(x) або f^(-1)(x), що допоможе вам відрізнити їх один від одного.
- Зверніть увагу, що зворотна функція зазвичай (але не завжди) є функціональною залежністю.[3]
Джерела
- Http://www.purplemath.com/modules/invrsfcn3.htm
- Http://www.mathsisfun.com/sets/function-inverse.html
- ↑ https://www.khanacademy.org/math/algebra2/manipulating-functions/introduction-to-inverses-of-functions/a/intro-to-inverse-functions
- ↑ Http://www.montereyinstitute.org/courses/DevelopmentalMath/COURSE_TEXT2_RESOURCE/U10_L1_T2_text_final.html
- ↑ Https://mathbitsnotebook.com/Algebra2/Functions/FNInverseFunctions.html
