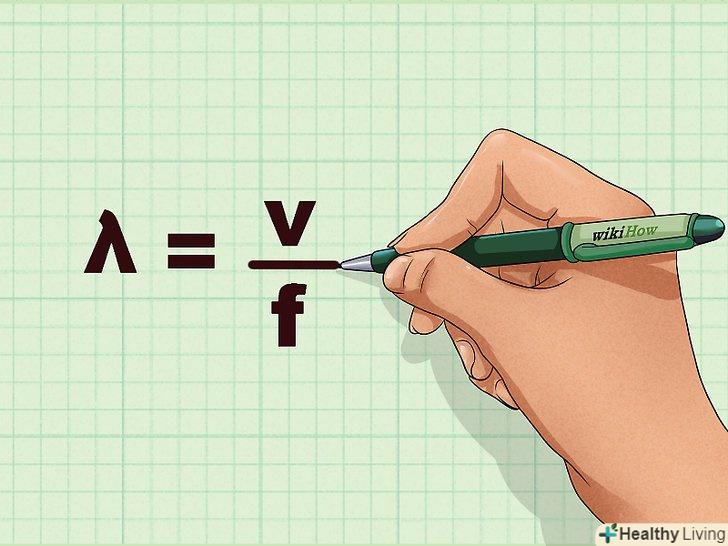Як розрахувати обертальний момент: 8 кроків

Найкраще визначення обертального моменту – це тенденція сили обертати предмет навколо осі, точки опори або точки обертання. Обертальний момент можна розрахувати за допомогою сили і плеча моменту (перпендикулярна відстань від осі до лінії дії сили), або використовуючи момент інерції і кутове прискорення.

Метод1З 2:

Використання сили і плеча моменту

Визначте сили, що діють на тіло і відповідні їм моменти. Якщо сила не перпендикулярна розглянутому плечу моменту (тобто вона діє під кутом), то вам може знадобитися знайти її складові з використанням тригонометричних функцій, таких як синус або косинус.
- Розглянута складова сили буде залежати від еквівалента перпендикулярної сили.
- Уявіть собі горизонтальний стрижень, до якого потрібно докласти силу 10 Н під кутом 30° над горизонтальною площиною, щоб обертати його навколо центру.
- Оскільки вам потрібно використовувати силу, не перпендикулярну плечу моменту, то для обертання стрижня вам необхідна вертикальна складова сили.
- Отже, потрібно розглядати y-складову, або використовувати F = 10sin30° Н.
Скористайтеся рівнянням моменту, τ = Fr, і просто замініть змінні заданими або отриманими даними.
- Простий приклад: Уявіть собі дитину масою 30 кг, що сидить на одному кінці гойдалки-дошки. Довжина одного боку гойдалки становить 1,5 м.
- Оскільки вісь обертання гойдалки знаходиться в центрі, вам не потрібно множити довжину.
- Вам необхідно визначити силу, що додається дитиною, за допомогою маси і прискорення.
- Оскільки дана маса, вам потрібно помножити її на прискорення вільного падіння, g, Рівне 9,81 м / с² . Отож:
- Тепер у вас є всі необхідні дані для використання рівняння моменту:
Скористайтеся знаками (плюс або мінус), щоб показати напрямок моменту. якщо сила обертає тіло за годинниковою стрілкою, то момент негативний. Якщо ж сила обертає тіло проти годинникової стрілки, то момент позитивний.
- У разі декількох прикладених сил, просто складіть всі моменти в тілі.
- Оскільки кожна сила прагне викликати різні напрямки обертання, важливо використовувати знак повороту для того, щоб стежити за напрямком дії кожної сили.
- Наприклад, до обода колеса, що має діаметр 0,050 м, були прикладені дві сили, F₁ = 10,0 Н, спрямована за годинниковою стрілкою, і F ₂ = 9,0 Н, спрямована проти годинникової стрілки.
- Оскільки дане тіло – коло, фіксована вісь є його центром. Вам потрібно розділити діаметр і отримати радіус. Розмір радіуса буде служити плечем моменту. Отже, радіус дорівнює 0,025 м.
- Для ясності ми можемо вирішити окремі рівняння для кожного з моментів, що виникають від відповідної сили.
- Для сили 1 дія спрямована за годинниковою стрілкою, отже, створюваний нею момент негативний:
- Для сили 2 дія спрямована проти годинникової стрілки, отже, створюваний нею момент позитивний:
- Тепер ми можемо скласти всі моменти, щоб отримати результуючий обертальний момент:

Метод2З 2:

Використання моменту інерції та кутового прискорення

Щоб почати вирішувати завдання, розберіться в тому, як діє момент інерції тіла. Момент інерції тіла-це опір тіла обертального руху. Момент інерції залежить як від маси, так і від характеру її розподілу.
- Щоб чітко розуміти це, уявіть собі два циліндри однакового діаметру, але різної маси.
- Уявіть собі, що вам потрібно повернути обидва циліндри навколо їх центральної осі.
- Очевидно, що циліндр з більшою масою буде складніше повернути, ніж інший циліндр, оскільки він "важче".
- А тепер уявіть собі два циліндра різних діаметрів, але однакової маси. Щоб виглядати циліндричними і мати різну масу, але в той же час мати різні діаметри, форма, або розподіл маси обох циліндрів повинна відрізнятися.
- Циліндр з великим діаметром буде виглядати як плоска закруглена пластина, тоді як менший циліндр буде виглядати як цілісна трубка з тканини.
- Циліндр з великим діаметром буде складніше обертати, оскільки вам потрібно докласти велику силу, щоб подолати більш довге плече моменту.
Виберіть рівняння, яке ви будете використовувати для розрахунку моменту інерції. є кілька рівнянь, які можна використовувати для цього.
- Перше рівняння-найпростіше: підсумовування мас і плечей моментів всіх частинок.
- Це рівняння використовується для матеріальних точок, або частинок. Ідеальна частка-це тіло, що має масу, але не займає простору.
- Іншими словами, єдиною значущою характеристикою цього тіла є маса; вам не потрібно знати його розмір, форму або будову.
- Ідея матеріальної частки широко використовується у фізиці з метою спрощення розрахунків і використання ідеальних і теоретичних схем.
- Тепер уявіть собі об'єкт на зразок порожнистого циліндра або суцільної рівномірної сфери. Ці предмети мають чітку і певну форму, розмір і будова.
- Отже, ви не можете розглядати їх як матеріальну точку.
- На щастя, можна використовувати формули, застосовні до деяких поширених об'єктів:
Знайдіть момент інерції. щоб почати розраховувати обертальний момент, потрібно знайти момент інерції. Скористайтеся наступним прикладом як керівництвом:
- Два невеликих "вантажу" масою 5,0 кг і 7,0 кг встановлені на відстані 4,0 м один від одного на легкому стрижні (масою якого можна знехтувати). Вісь обертання знаходиться в середині стрижня. Стрижень розкручується зі стану спокою до кутової швидкості 30,0 рад/с за 3,00 с.розрахуйте вироблений обертальний момент.
- Оскільки вісь обертання знаходиться в середині стрижня, то плече моменту обох вантажів дорівнює половині його довжини, тобто 2,0 м.
- Оскільки форма, розмір і будова "вантажів" не обумовлюється, ми можемо припустити, що вантажі є матеріальними частинками.
- Момент інерції можна обчислити наступним чином:
Знайдіть кутове прискорення, α. для розрахунку кутового прискорення можна скористатися формулою α= at/r.
- Перша формула, α= at / r, може використовуватися в тому випадку, якщо дано тангенціальне прискорення і радіус.
- Тангенціальне прискорення-це прискорення, спрямоване по дотичній до напрямку руху.
- Уявіть собі об'єкт, що рухається по криволінійному шляху. Тангенціальне прискорення-це просто його лінійне прискорення на будь-який з точок всього шляху.
- У випадку другої формули, найлегше проілюструвати її, пов'язавши з поняттями з кінематики: зміщенням, лінійною швидкістю і лінійним прискоренням.
- Зміщення-це відстань, пройдену об'єктом( одиниця Сі-метри, м); лінійна швидкість-це показник зміни зміщення за одиницю часу( одиниця сі-м/с); лінійне прискорення - це показник зміни лінійної швидкості за одиницю часу (одиниця сі-м / с² ).
- Тепер давайте розглянемо аналоги цих величин при обертальному русі: кутове зміщення, θ – кут повороту певної точки або відрізка (одиниця Сі – рад); кутова швидкість, ω-зміна кутового зміщення за одиницю часу (одиниця Сі – рад/с); і кутове прискорення, α – зміна кутової швидкості за одиницю часу (одиниця Сі-рад / с² ).
- Повертаючись до нашого прикладу-нам були дані для кутового моменту і час. Оскільки обертання починалося зі стану спокою, то початкова кутова швидкість дорівнює 0. Ми можемо скористатися рівнянням, щоб знайти:
Скористайтеся рівнянням, τ = Iα, щоб знайти обертальний момент. просто замініть змінні відповідями, отриманими на попередніх кроках.
- Ви можете помітити, що одиниця " рад " не підходить до наших одиниць виміру, оскільки вважається безрозмірною величиною.
- Це означає, що ви можете знехтувати нею і продовжити Ваші розрахунки.
- Для аналізу одиниць вимірювання ми можемо виразити кутове прискорення в с^-2 .

Поради

У першому методі, якщо тіло є колом і вісь його обертання знаходиться в центрі, то розраховувати складові сили не потрібно (за умови, що сила не прикладена під нахилом), оскільки сила лежить на дотичній до кола, тобто перпендикулярно плечу моменту.
Якщо вам складно уявити, як відбувається обертання, то візьміть ручку і спробуйте відтворити завдання. Для більш точного відтворення не забудьте скопіювати положення осі обертання і напрямок прикладеної сили.