Трапеція є чотирикутником, у якого дві паралельні сторони (підстави) мають різну довжину. Формула для обчислення площі трапеції: S = ½ (b1+b2)h, де b1 і b2 — підстави, h — висота трапеції. Якщо відомі тільки бічні сторони правильної трапеції, її можна розбити на ряд простих фігур, щоб знайти висоту, а потім обчислити площу.
Кроки
Метод1 З 2:
Обчислення площі по висоті і підставах
Метод1 З 2:
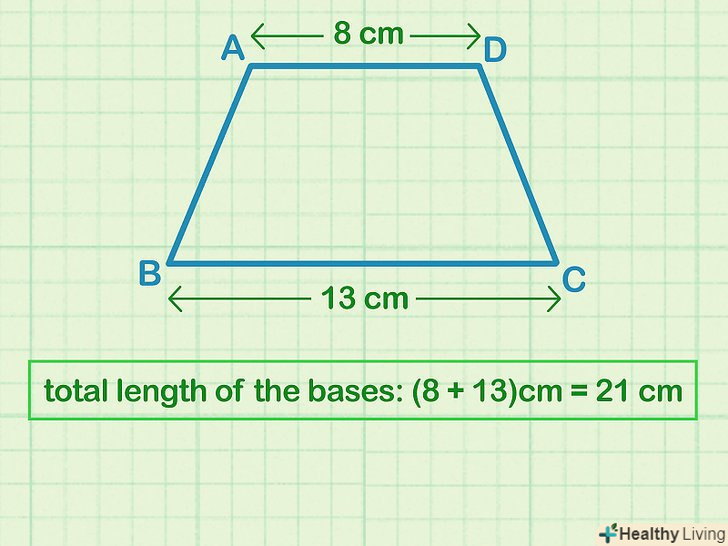
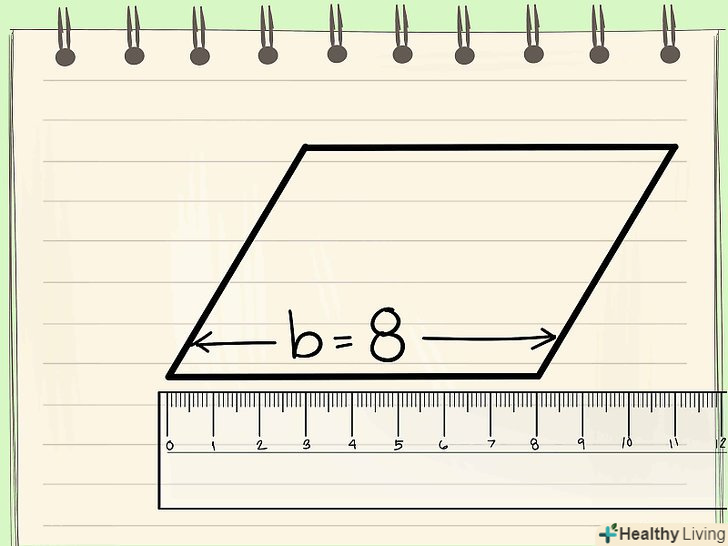
 Складіть підстави.підстави-це дві сторони трапеції, які паралельні один одному. Якщо значення підстав не дані, виміряйте їх лінійкою, а потім складіть отримані значення.[1]
Складіть підстави.підстави-це дві сторони трапеції, які паралельні один одному. Якщо значення підстав не дані, виміряйте їх лінійкою, а потім складіть отримані значення.[1]- Наприклад, якщо верхня основа (b1) дорівнює 8 см, а нижня (b2 ) - 13 см, сума підстав b = b1 + b2 = 8 + 13 = 21 см.
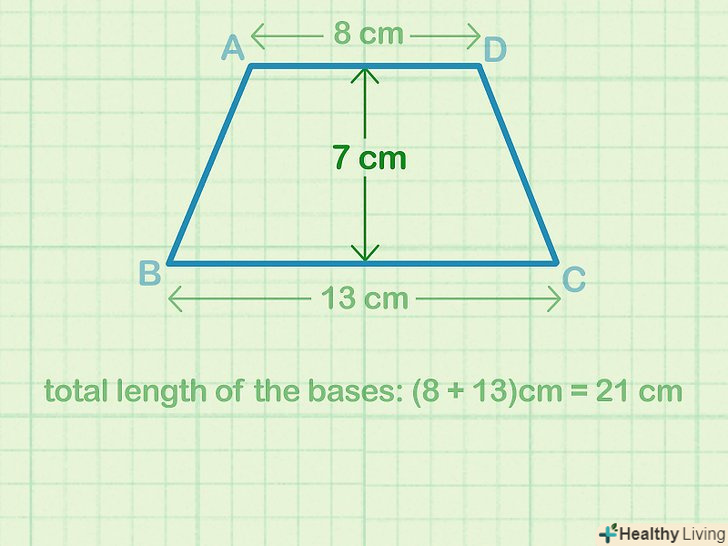
 Виміряйте висоту трапеції. Висота трапеції — це відстань між паралельними підставами. Проведіть перпендикуляр до підстав, а потім за допомогою лінійки виміряйте його і запишіть знайдене значення.[2]
Виміряйте висоту трапеції. Висота трапеції — це відстань між паралельними підставами. Проведіть перпендикуляр до підстав, а потім за допомогою лінійки виміряйте його і запишіть знайдене значення.[2]- Пам'ятайте, що висота не дорівнює бічним сторонам трапеції. Висота дорівнює бічній стороні трапеції, тільки якщо ця сторона перпендикулярна підставам.
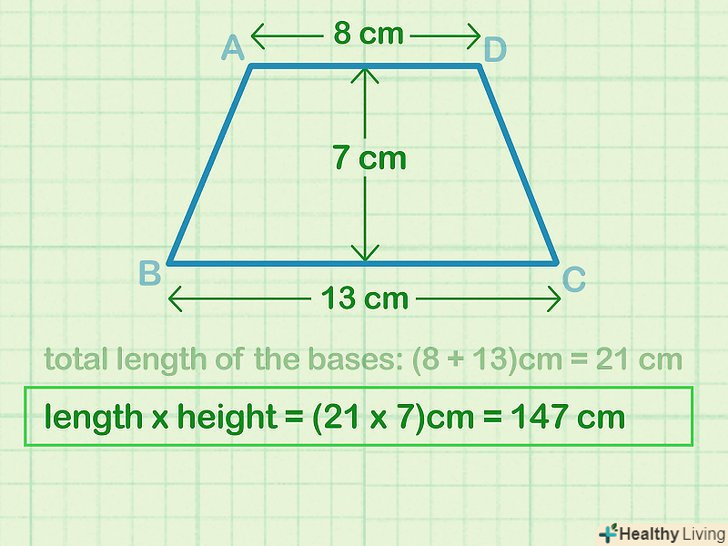
 Перемножте суму підстав і висоту. тобто помножте значення "b «На значення»h". Результат запишіть в квадратних одиницях виміру.[3]
Перемножте суму підстав і висоту. тобто помножте значення "b «На значення»h". Результат запишіть в квадратних одиницях виміру.[3]- У нашому прикладі: 21 x 8 = 147 см2.
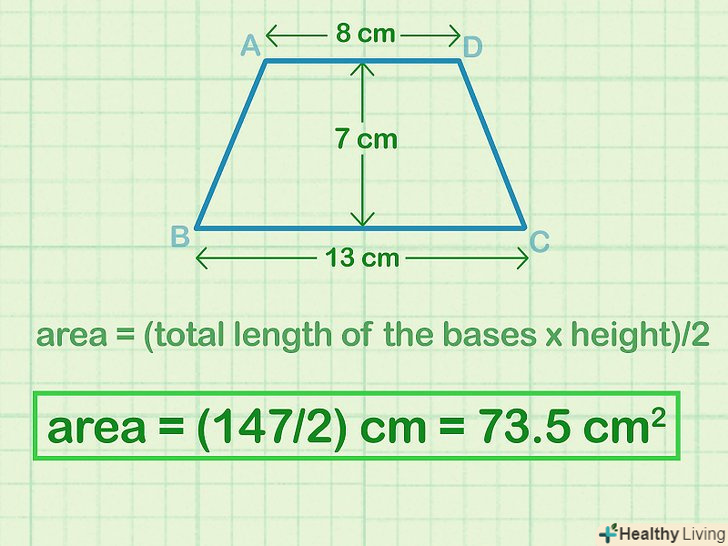
 Розділіть знайдене значення на 2, щоб знайти площу трапеції. Також знайдене значення можна помножити на½. Результат запишіть в квадратних одиницях виміру.[4]
Розділіть знайдене значення на 2, щоб знайти площу трапеції. Також знайдене значення можна помножити на½. Результат запишіть в квадратних одиницях виміру.[4]- У нашому прикладі: S = 147/2 = 73,5 см2.
Метод2 З 2:
Обчислення площі по бічних сторонах
Метод2 З 2:
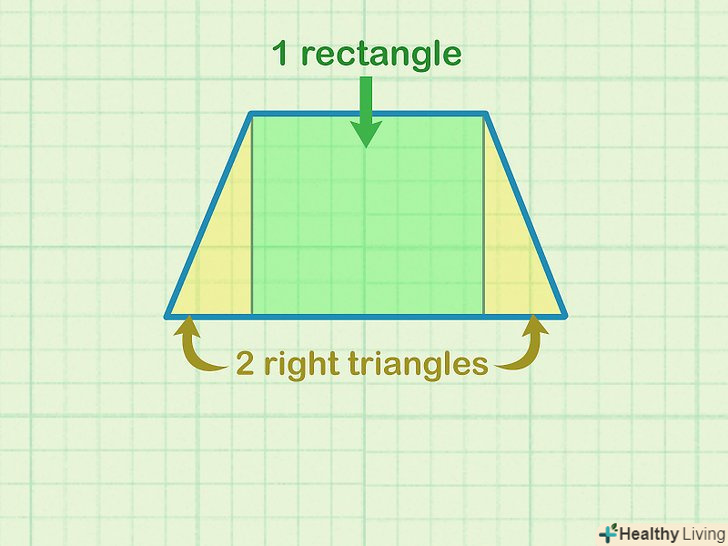
 Розбийте трапецію на 1 прямокутник і 2 прямокутних трикутника.проведіть два перпендикуляри з вершин трапеції на нижню основу. Так ви отримаєте 1 прямокутник (посередині) і 2 прямокутних рівних трикутника (з боків).[5]
Розбийте трапецію на 1 прямокутник і 2 прямокутних трикутника.проведіть два перпендикуляри з вершин трапеції на нижню основу. Так ви отримаєте 1 прямокутник (посередині) і 2 прямокутних рівних трикутника (з боків).[5]- Цей метод можна застосувати тільки до правильної трапеції.
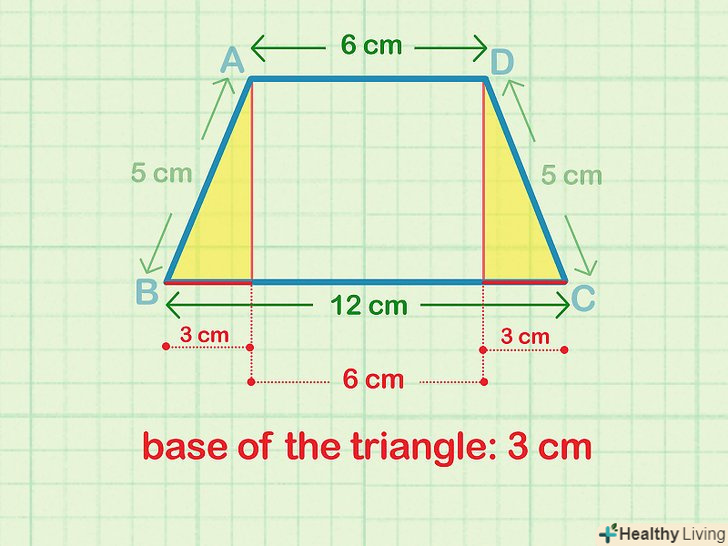
 Знайдіть основу прямокутного трикутника.для цього спочатку відніміть верхню основу з нижньої основи. Тепер знайдене значення розділіть на 2, щоб обчислити підставу трикутника. На даному етапі вам відомі підстава і гіпотенуза трикутника.[6]
Знайдіть основу прямокутного трикутника.для цього спочатку відніміть верхню основу з нижньої основи. Тепер знайдене значення розділіть на 2, щоб обчислити підставу трикутника. На даному етапі вам відомі підстава і гіпотенуза трикутника.[6]- Наприклад, якщо верхня основа (b1) трапеції дорівнює 6 см, а нижня основа (b2) дорівнює 12 см, підстава трикутника дорівнює 3 см (тому що b = (b2 - b1)/2 = (12 - 6)/2 = 3 см).
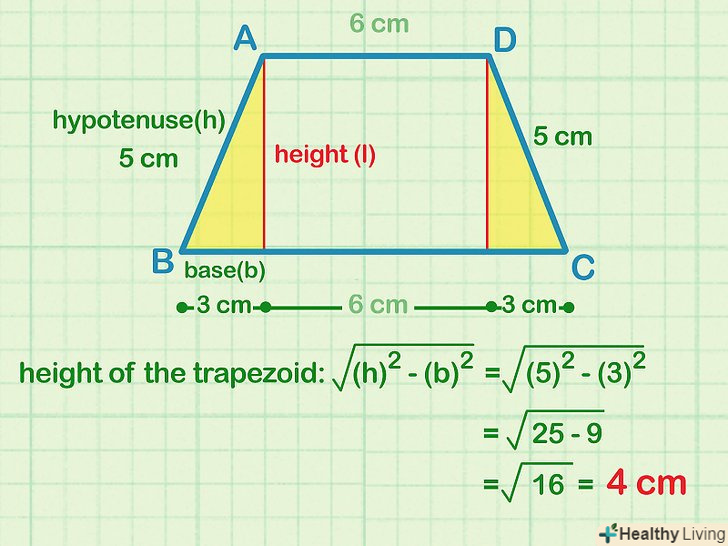
 Знайдіть висоту трапеції за теоремою Піфагора. для цього підставте значення підстави і гіпотенузи трикутника в формулу A2 + B2 = C2, де A — підстава, C — гіпотенуза. Знайдіть значення B, тобто висоту трапеції. Якщо основа трикутника дорівнює 3 см, а гіпотенуза дорівнює 5 см:[7]
Знайдіть висоту трапеції за теоремою Піфагора. для цього підставте значення підстави і гіпотенузи трикутника в формулу A2 + B2 = C2, де A — підстава, C — гіпотенуза. Знайдіть значення B, тобто висоту трапеції. Якщо основа трикутника дорівнює 3 см, а гіпотенуза дорівнює 5 см:[7]- Підставте значення: 32 + B2 = 52
- Зведіть в квадрат: 9 + B2 = 25
- Відніміть 9 з кожної сторони рівняння: B2 = 16
- Витягніть квадратний корінь з кожної сторони рівняння: B = 4 см
Підказка: якщо в рівнянні немає ідеального квадрата, спростіть відповідь і залиште квадратний корінь. Наприклад, √32 = √(16)(2) = 4√2.
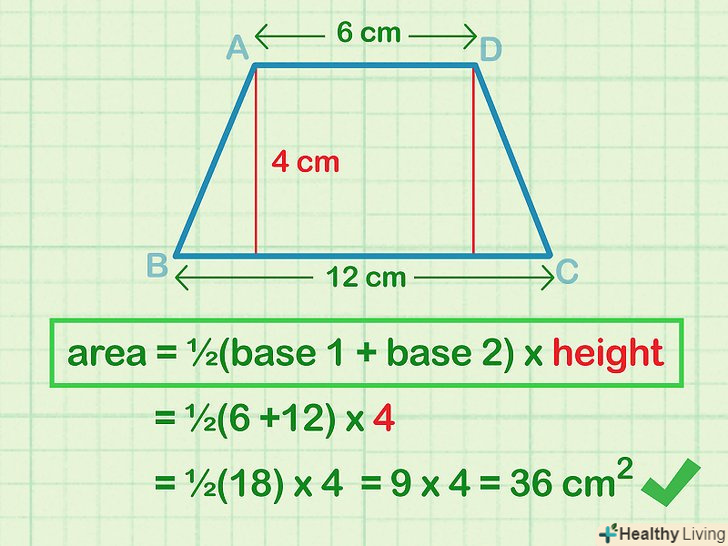
 Підставте значення підстав і висоти в формулу для обчислення площі трапеції. Формула: S = ½ (b1 + b2)h. Результат запишіть в квадратних одиницях виміру.[8]
Підставте значення підстав і висоти в формулу для обчислення площі трапеції. Формула: S = ½ (b1 + b2)h. Результат запишіть в квадратних одиницях виміру.[8]- Запишіть формулу: S = ½ (b1 + b2)h
- Підставте значення: S = (6 + 12)(4)
- Спростіть вираз і перемножте числа: S = ½(18)(4)
- Відповідь: S = 36 см2.
Поради
- Якщо вам відома медіана трапеції (відрізок, який з'єднує середини бічних сторін трапеції і паралельний підстав трапеції), помножте її на висоту, щоб знайти площу.[9]
Джерела
- ↑ Https://youtu.be/9hISqaDb6XE?t=44
- ↑ Https://youtu.be/9hISqaDb6XE?t=34
- ↑ Https://youtu.be/9hISqaDb6XE?t=78
- ↑ Https://youtu.be/9hISqaDb6XE?t=73
- ↑ Https://www.mathopenref.com/trapezoidarea.html
- ↑ Https://www.mathopenref.com/trapezoidarea.html
- ↑ Https://youtu.be/5KmCDSI3n-8?t=87
- ↑ Https://www.mathopenref.com/trapezoidarea.html
- ↑ Https://www.mathopenref.com/trapezoidmedian.html