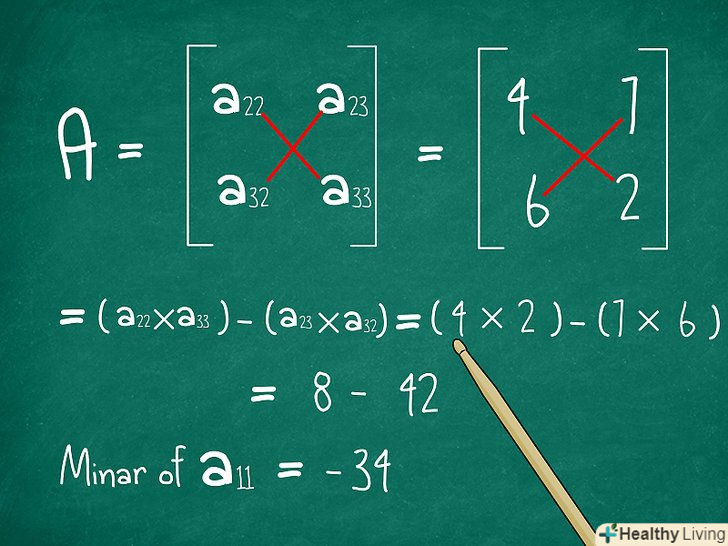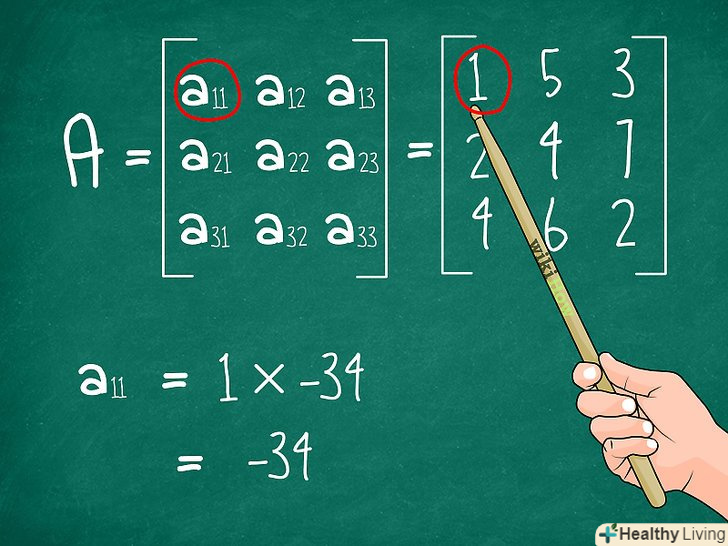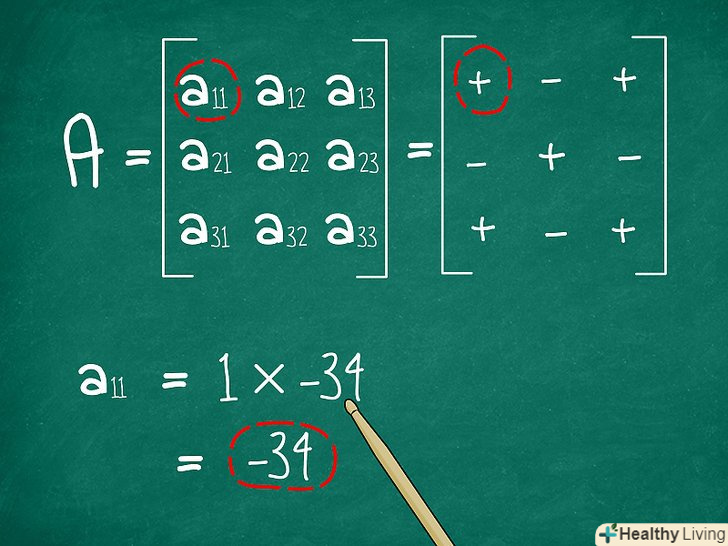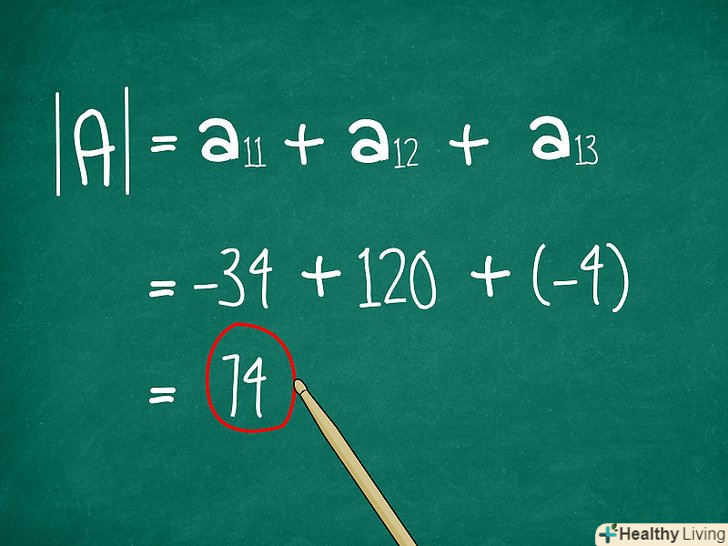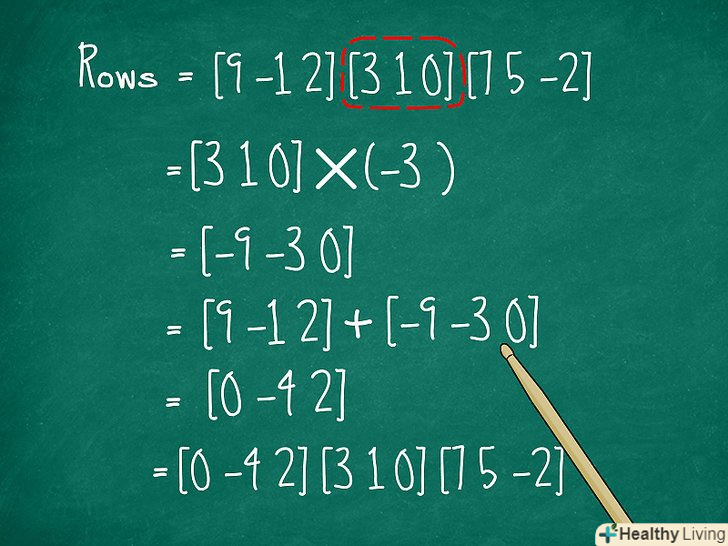Визначники матриць часто використовуються в обчисленнях, в лінійній алгебрі та аналітичній геометрії. Поза академічним світом визначники матриць постійно потрібні інженерам і програмістам, особливо тим, хто працює з комп'ютерною графікою. Якщо ви вже знаєте, як знайти визначник матриці розмірністю 2x2, то з інструментів для знаходження визначника матриці 3x3 вам будуть необхідні тільки додавання, віднімання і множення.
Кроки
Метод1 З 2:
Пошук визначника
Метод1 З 2:
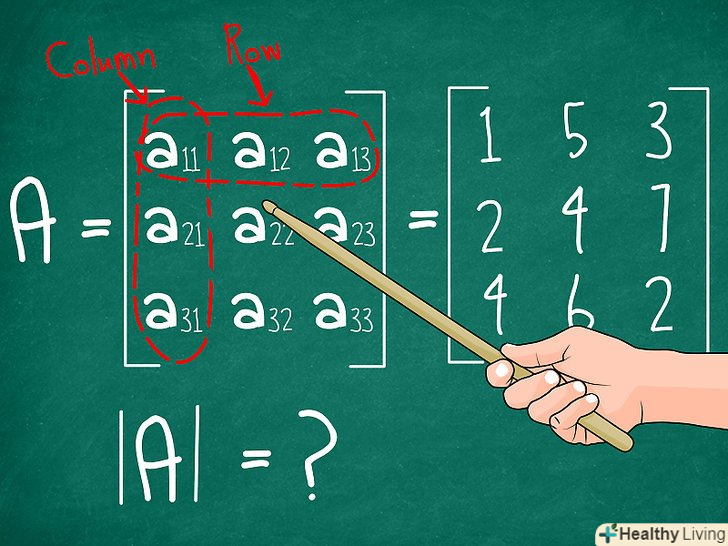
 Запишіть матрицю розмірністю 3 x 3.<|b||b> запишемо матрицю розмірністю 3 x 3, яку позначимо M, і знайдемо її визначник|M/. Далі наводиться загальна форма запису матриці, яку ми будемо використовувати, і матриця для нашого прикладу:
Запишіть матрицю розмірністю 3 x 3.<|b||b> запишемо матрицю розмірністю 3 x 3, яку позначимо M, і знайдемо її визначник|M/. Далі наводиться загальна форма запису матриці, яку ми будемо використовувати, і матриця для нашого прикладу: Виберіть рядок або стовпець матриці. цей рядок (або стовпець) буде опорною. Результат буде однаковий, незалежно від того, який рядок або який стовпець ви виберете. В даному прикладі Давайте візьмемо перший рядок. Трохи пізніше ви знайдете кілька порад щодо того, як вибирати рядок або стовпець, щоб спростити обчислення.
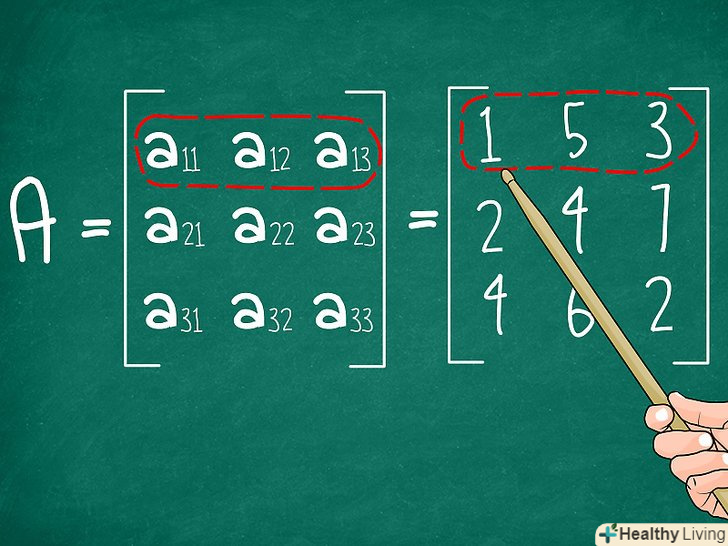
Виберіть рядок або стовпець матриці. цей рядок (або стовпець) буде опорною. Результат буде однаковий, незалежно від того, який рядок або який стовпець ви виберете. В даному прикладі Давайте візьмемо перший рядок. Трохи пізніше ви знайдете кілька порад щодо того, як вибирати рядок або стовпець, щоб спростити обчислення.- Давайте виберемо перший рядок матриці M в нашому прикладі. Обведіть числа 1 5 3. У загальній формі обведіть a11 a12 a13.
 Закресліть рядок або стовпець з першим елементом. зверніться до опорного рядка (або до опорного стовпця) і виберіть перший елемент. Проведіть горизонтальну і вертикальну риску через цей елемент, викресливши таким чином стовпець і Рядок з цим елементом. Має залишитися чотири числа. Будемо вважати ці елементи новою матрицею розмірністю 2 x 2.
Закресліть рядок або стовпець з першим елементом. зверніться до опорного рядка (або до опорного стовпця) і виберіть перший елемент. Проведіть горизонтальну і вертикальну риску через цей елемент, викресливши таким чином стовпець і Рядок з цим елементом. Має залишитися чотири числа. Будемо вважати ці елементи новою матрицею розмірністю 2 x 2.- У нашому прикладі, опорним рядком буде 1 5 3.перший елемент знаходиться на перетині першого стовпця і першого рядка. Викресліть рядок і стовпець з цим елементом, тобто перший і перший стовпець. Запишіть залишилися елементи у вигляді матриці 2 x 2:
1 5 324 746 2
 Знайдіть визначник матриці 2 x 2. Запам'ятайте, що визначник матриці
Знайдіть визначник матриці 2 x 2. Запам'ятайте, що визначник матриціобчислюється як Ad - bc.[1] спираючись на це, Ви можете обчислити визначник отриманої матриці 2 x 2, Яку, якщо хочете, можете позначити як X. помножте два числа матриці X, з'єднаних по діагоналі зліва направо (тобто так: \ ). Потім відніміть результат множення двох інших чисел по діагоналі справа наліво (тобто так: / ). Використовуйте цю формулу, щоб обчислити визначник матриці, яку ви тільки що отримали.
- У нашому прикладі визначник матриці
= 4*2 - 7*6 = -34.
- Цей визначник називаєтьсяМінором елемента, який ми вибрали в нашій первісній матриці.[2] іншими словами, Ми тільки що знайшли мінор a11.
- У нашому прикладі визначник матриці
 Помножте отриману відповідь на вибраний елемент матриці M. згадайте, який елемент з опорного рядка (або стовпця) ми використовували, коли викреслювали інші елементи рядка і стовпця, щоб отримати нову матрицю. Помножте цей елемент на отриманий мінор (визначник матриці 2x2, яку ми позначили X).
Помножте отриману відповідь на вибраний елемент матриці M. згадайте, який елемент з опорного рядка (або стовпця) ми використовували, коли викреслювали інші елементи рядка і стовпця, щоб отримати нову матрицю. Помножте цей елемент на отриманий мінор (визначник матриці 2x2, яку ми позначили X).- У нашому прикладі ми вибирали елемент a11, який дорівнював 1. Помножимо його на -34 (визначник матриці 2x2), і у нас вийде 1*-34 = -34.
 Визначте знак отриманого результату.далі вам знадобиться помножити отриманий результат на 1, або на -1, щоб отримати алгебраїчне доповнення (кофактор) вибраного елемента. Знак кофактора буде залежати від того, в якому місці матриці 3x3 стоїть елемент. Запам'ятайте цю просту схему знаків, щоб знати знак кофактора:
Визначте знак отриманого результату.далі вам знадобиться помножити отриманий результат на 1, або на -1, щоб отримати алгебраїчне доповнення (кофактор) вибраного елемента. Знак кофактора буде залежати від того, в якому місці матриці 3x3 стоїть елемент. Запам'ятайте цю просту схему знаків, щоб знати знак кофактора:- + - +
- - + -
- + - +
- Оскільки ми працювали з елементомa11, для якого стоїть знак +, то ми будемо множити отримане значення на +1 (тобто залишимо його як є). Алгебраїчне доповнення нашого елемента дорівнюватиме -34.
- Ви також можете знайти знак алгебраїчного Доповнення за формулою (-1)i + j, де i і j - номер стовпця і рядка вибраного елемента відповідно.[3]
 Повторіть всі вищеописані дії з другим елементом опорного рядка (або стовпця).поверніться до вихідної матриці розмірністю 3x3 і рядку, яку ми обвели на самому початку обчислень. Повторіть всі дії з цим елементом:
Повторіть всі вищеописані дії з другим елементом опорного рядка (або стовпця).поверніться до вихідної матриці розмірністю 3x3 і рядку, яку ми обвели на самому початку обчислень. Повторіть всі дії з цим елементом:- Викресліть рядок і стовпець з цим елементом. у нашому прикладі ми повинні вибрати елемент a12 (рівний 5). Викреслимо перший рядок (1 5 3) і другий стовпець
матриці.
- Запишіть залишилися елементи у вигляді матриці 2x2. у нашому прикладі матриця матиме вигляд
- Знайдіть визначник цієї нової матриці 2x2.скористайтеся наведеною вище формулою ad-bc. (2*2 - 7*4 = -24)
- Помножте отриманий визначник на вибраний елемент матриці 3x3. -24 * 5 = -120
- Перевірте, чи потрібно помножити результат на -1. скористаємося формулою (-1)ij , щоб визначити знак алгебраїчного Доповнення. Для обраного нами елемента a12 в таблиці вказано знак «-», аналогічний результат дає і формула. Тобто ми повинні змінити знак: (-1)*(-120) = 120.
- Викресліть рядок і стовпець з цим елементом. у нашому прикладі ми повинні вибрати елемент a12 (рівний 5). Викреслимо перший рядок (1 5 3) і другий стовпець
 Повторіть з третім елементом.далі вам знадобиться знайти ще одне алгебраїчне доповнення. Обчисліть його для останнього елемента опорного рядка або опорного стовпця. Далі наводиться короткий опис того, як обчислюється алгебраїчне доповнення для a13 в нашому прикладі:
Повторіть з третім елементом.далі вам знадобиться знайти ще одне алгебраїчне доповнення. Обчисліть його для останнього елемента опорного рядка або опорного стовпця. Далі наводиться короткий опис того, як обчислюється алгебраїчне доповнення для a13 в нашому прикладі:- Закресліть перший рядок і третій стовпець, щоб отримати матрицю
- Її визначник дорівнює 2*6 - 4*4 = -4.
- Помножте результат на елемент a13: -4 * 3 = -12.
- Елемент a13 має знак + у наведеній вище таблиці, тому відповідь буде -12.
- Закресліть перший рядок і третій стовпець, щоб отримати матрицю
 Складіть отримані результати. Це останній крок. Вам необхідно скласти отримані алгебраїчні доповнення елементів опорного рядка (або опорного стовпця). Складіть їх разом, і ви отримаєте значення визначника матриці 3x3.
Складіть отримані результати. Це останній крок. Вам необхідно скласти отримані алгебраїчні доповнення елементів опорного рядка (або опорного стовпця). Складіть їх разом, і ви отримаєте значення визначника матриці 3x3.- У нашому прикладі визначник дорівнює-34 + 120 + -12 = 74.
Метод2 З 2:
Як спростити завдання
Метод2 З 2:
 Вибирайте в якості опорного рядка (або стовпця) ту, що має більше нулів.Пам'ятайте, що в якості опорної ви можете вибрати будь-яку рядок або стовпець. Вибір опорного рядка або стовпця не впливає на результат. Якщо ви виберете рядок з найбільшою кількістю нулів, вам доведеться виконувати менше обчислень, оскільки вам буде необхідно обчислити алгебраїчні доповнення тільки для ненульових елементів. Ось чому:
Вибирайте в якості опорного рядка (або стовпця) ту, що має більше нулів.Пам'ятайте, що в якості опорної ви можете вибрати будь-яку рядок або стовпець. Вибір опорного рядка або стовпця не впливає на результат. Якщо ви виберете рядок з найбільшою кількістю нулів, вам доведеться виконувати менше обчислень, оскільки вам буде необхідно обчислити алгебраїчні доповнення тільки для ненульових елементів. Ось чому:- Припустимо, ви вибрали 2 рядок з елементами a21, a22, and a23. Щоб знайти визначник, вам буде необхідно знайти визначники трьох різних матриць розмірністю 2x2. Давайте назвемо їх a21, a22, and A23.
- Тобто визначник матриці 3x3 дорівнює a21|A21| - a22|A22| + a23|a23|.
- Якщо обидва елементи a22 і a23 дорівнюють 0, то наша формула стає набагато коротшою a21|A21| - 0*| a22| + 0*| a23| = a21 / a21| - 0 + 0 = a21|a21|. Тобто необхідно обчислити тільки алгебраїчне доповнення одного елемента.
 Використовуйте додавання рядків, щоб спростити матрицю.якщо ви візьмете один рядок і додасте до неї іншу, то визначник матриці не зміниться. Те ж саме стосується і стовпців. Подібні дії можна виконувати кілька разів, крім того, ви можете множити значення рядка на постійну (перед складанням) для того, щоб отримати якомога більше нулів. Подібні дії можуть заощадити масу часу.
Використовуйте додавання рядків, щоб спростити матрицю.якщо ви візьмете один рядок і додасте до неї іншу, то визначник матриці не зміниться. Те ж саме стосується і стовпців. Подібні дії можна виконувати кілька разів, крім того, ви можете множити значення рядка на постійну (перед складанням) для того, щоб отримати якомога більше нулів. Подібні дії можуть заощадити масу часу.- Наприклад, у нас є матриця з трьох рядків:
- Щоб позбутися від 9 на місці елемента a11, ми можемо помножити другий рядок на -3 і додати результат до першої. Новий перший рядок буде [9 -1 2] + [-9 -3 0] = [0 -4 2].
- Тобто ми отримуємо нову матрицю
Спробуйте виконати те ж саме зі стовпцями, щоб отримати на місці елемента a12 нуль.
- Наприклад, у нас є матриця з трьох рядків:
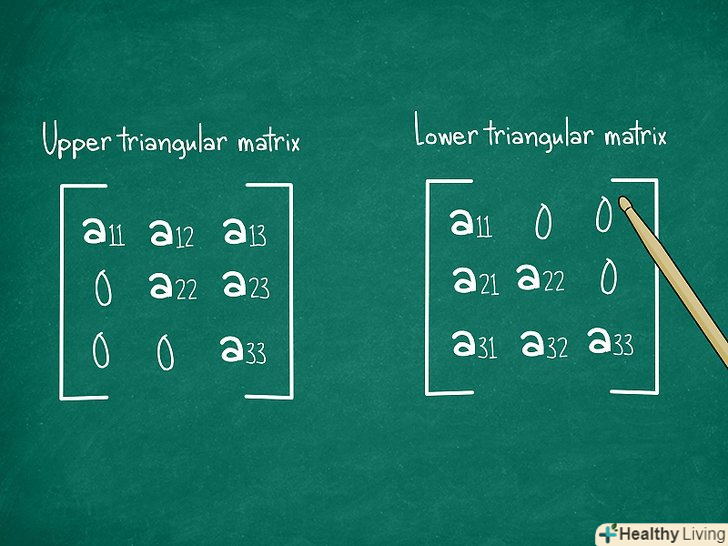
 Пам'ятайте, що обчислювати визначник трикутних матриць набагато простіше. визначник трикутних матриць обчислюється як добуток елементів на головній діагоналі, від a 11 у верхньому лівому куті до a33 у нижньому правому куті. Мова в даному випадку йде про трикутних матрицях розмірністю 3x3. Трикутні матриці можуть бути наступних видів, залежно від розташування ненульових значень:[4]
Пам'ятайте, що обчислювати визначник трикутних матриць набагато простіше. визначник трикутних матриць обчислюється як добуток елементів на головній діагоналі, від a 11 у верхньому лівому куті до a33 у нижньому правому куті. Мова в даному випадку йде про трикутних матрицях розмірністю 3x3. Трикутні матриці можуть бути наступних видів, залежно від розташування ненульових значень:[4]- Верхня трикутна матриця: всі ненульові елементи знаходяться на головній діагоналі і вище неї. Всі елементи нижче головної діагоналі дорівнюють нулю.
- Нижня трикутна матриця: всі ненульові елементи знаходяться нижче головної діагоналі і на ній.
- Діагональна матриця: всі ненульові елементи знаходяться на головній діагоналі. Є окремим випадком вищеописаних матриць.
Поради
- Описаний метод поширюється на квадратні матриці будь-якого рангу. Наприклад, якщо ви використовуєте його для матриці 4x4, то після «викреслювання» будуть залишатися матриці 3x3, для яких визначник буде обчислюватися вищезгаданим способом. Будьте готові до того, що обчислювати визначник для матриць таких розмірностей вручну — дуже трудомістке завдання!
- Якщо всі елементи рядка або стовпця рівні 0, то визначник матриці теж дорівнює 0.
Джерела
- ↑ Https://www.khanacademy.org/math/precalculus/precalc-matrices/inverting_matrices/v/finding-the-determinant-of-a-2x2-matrix
- ↑ Https://people.richland.edu/james/lecture/m116/matrices/determinant.html
- ↑ Http://www.math.rutgers.edu/~cherlin/Courses/250/Lectures/250L12.html
- ↑ Https://people.richland.edu/james/lecture/m116/matrices/determinant.html