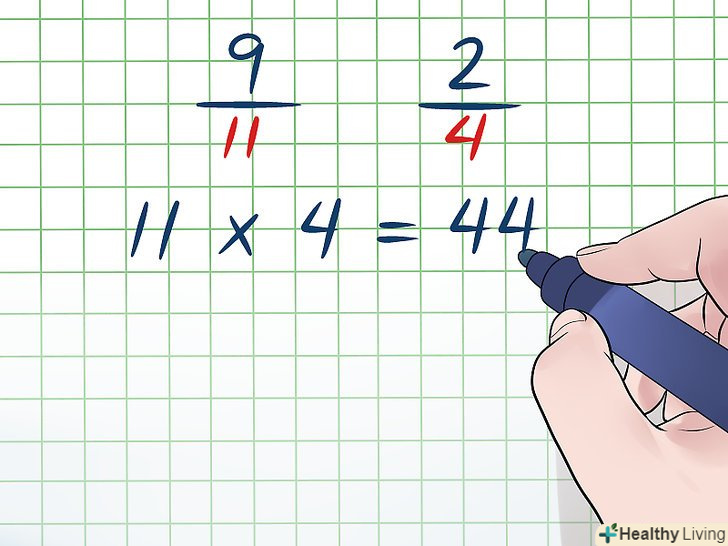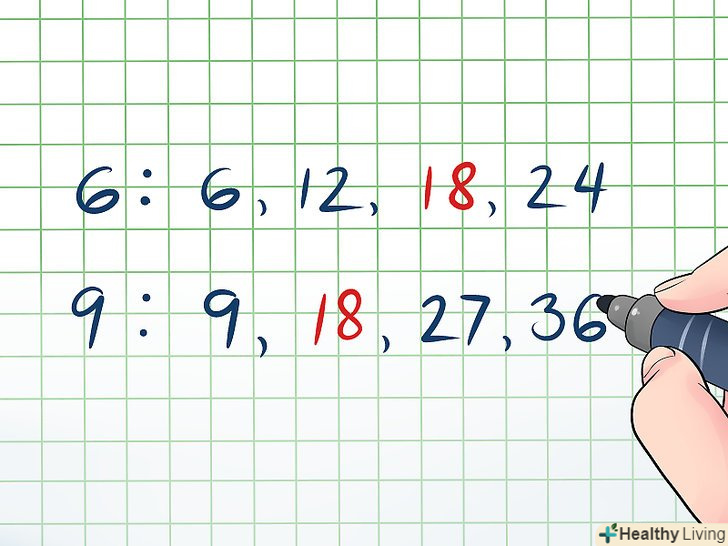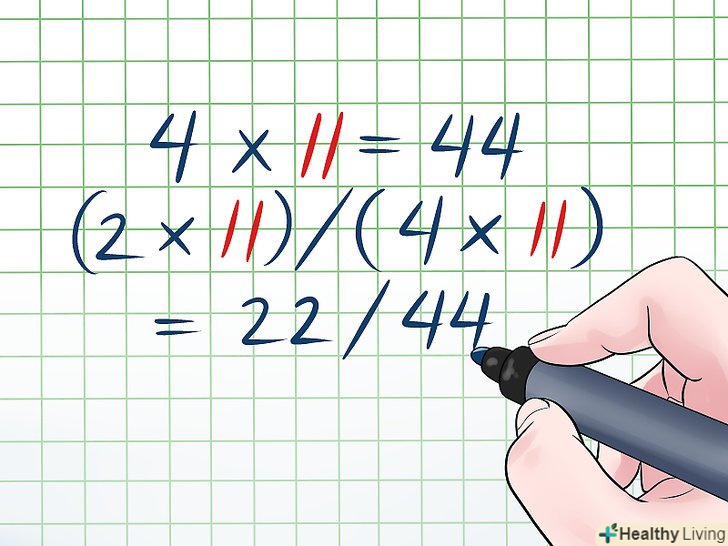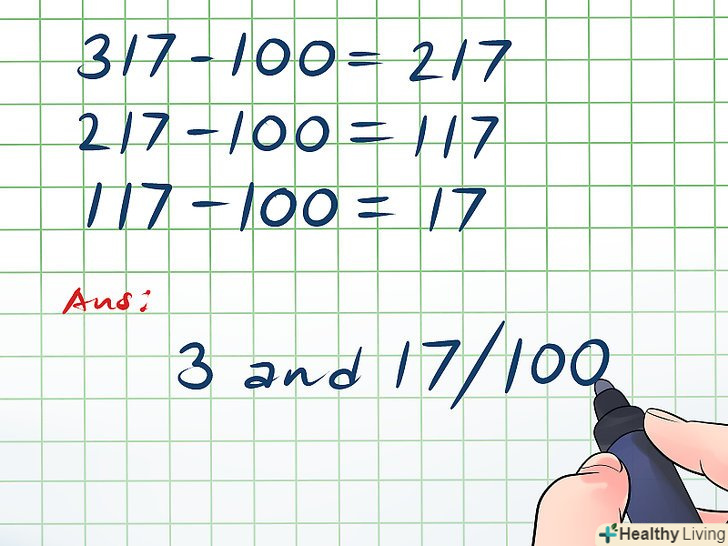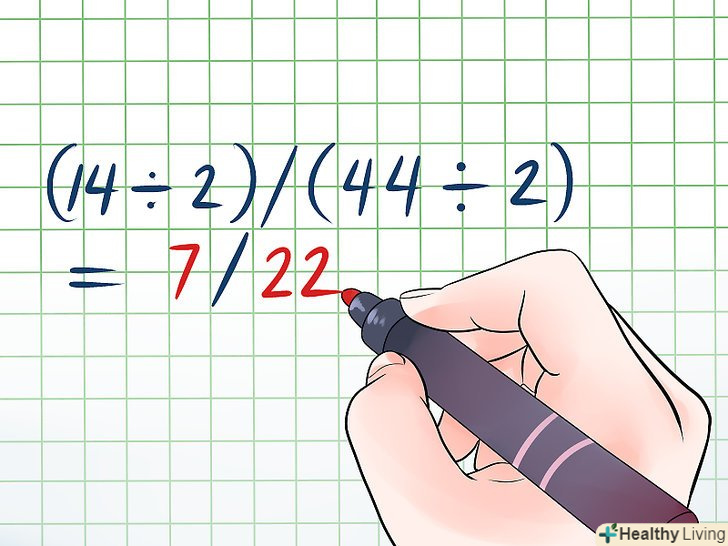1. Головна
    2. Математика
    3. Як складати і віднімати дроби з різними знаменниками

Як складати і віднімати дроби з різними знаменниками

Для того щоб складати і віднімати дроби з різними знаменниками, вам потрібно привести їх до спільного знаменника. Процеси додавання і віднімання дробів дуже схожі; тільки на кінцевому етапі ви повинні або скласти, або відняти чисельники дробів. Якщо ви хочете навчитися складати і віднімати дроби з різними знаменниками, виконайте наступні дії.

Частина1 З 2:
Знаходження спільного знаменника

  1. Запишіть дроби поруч один з одним.напишіть їх так, щоб чисельники дробів (верхні числа) і знаменники дробів (Нижні числа) розташовувалися навпроти один одного. Наприклад, розглянемо дроби 9/11 і 2/4.
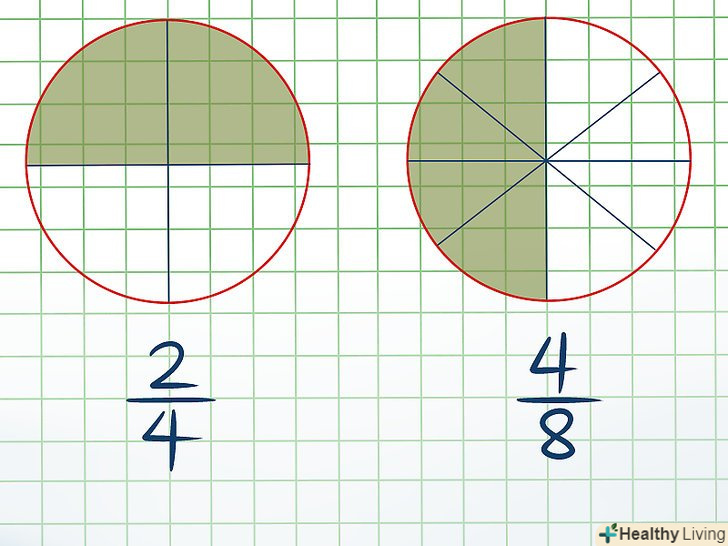
  2. Зрозумійте, що таке еквівалентні дроби. якщо помножити чисельник і знаменник певної дробу на деяке число, то ви отримаєте еквівалентну дріб, рівну вихідної дробу. Наприклад, якщо ви помножите дріб 2/4 на 2, Ви отримаєте дріб 4/8, яка дорівнює (еквівалентна) вихідної дробу 2/4. Ви можете перевірити це наступним чином:
    • Намалюйте коло, розділіть його на чотири рівні частини і зафарбуйте дві з них (2/4).
    • Намалюйте ще одне коло, розділіть його на 8 рівних частин і зафарбуйте чотири з них (4/8).
    • Порівняйте зафарбовані області обох кіл; вони відповідають дробам 2/4 і 4/8. Розмір зафарбованих областей буде однаковим.
  3. Перемножте два знаменники, щоб знайти спільний знаменник. для того щоб скласти або відняти дроби, потрібно привести їх до спільного знаменника; спільний знаменник – це число, дільниками якого є знаменники даних дробів. Найпростіший спосіб знайти спільний знаменник дробів - це перемножити їх знаменники. Зробивши це, переходьте до наступного розділу або продовжуйте читати цей розділ і дізнаєтеся, як знайти найменший спільний знаменник (НОЗ).
    • У нашому прикладі 11 і 4 – це знаменники дробів 9 /11 і 2 / 4
    • Перемножте ці знаменники: 11 x 4 =44.
  4. Знайдіть найменший спільний знаменник (НОЗ). це найменше число, яке ділиться на знаменники даних дробів. Для обчислення НОЗ запишіть кратні кожного знаменника даних дробів. Підкресліть найменше число, яке зустрічається в обох списках. На цей раз розглянемо такий приклад: 5/6 + 2/9.
    • У нашому прикладі знаменники рівні 6 і 9, тому для першого знаменника пишіть числа, що діляться на 6, а для другого – на 9.
    • Кратні6: 6, 12, 18, 24
    • Кратні9: 9,18 , 27, 36
    • Так як число18 – це найменше число, що знаходиться в обох списках, то НОЗ = 18.

Частина2 З 2:
Рішення задачі

  1. Перетворіть перший дріб в еквівалентну, знаменник якої дорівнює спільному знаменнику.у нашому першому прикладі (дроби 9/11 і 2/4) загальний знаменник дорівнює 44. Але пам'ятайте, що ви не можете змінити знаменник дробу без зміни його чисельника.
    • Розділіть знайдений спільний знаменник на знаменник першого дробу: 44 ÷ 11 =4
    • Помножте чисельник і знаменник першого дробу на отримане значення.
    • (9 x4 ) / (11 x 4) = 36/44
  2. Виконайте те ж саме з другим дробом.ось як перетворити дріб 2/4 в еквівалентну дріб зі знаменником 44:
    • 44 ÷ 4 =11
    • (2 x11) / (4 x 11) = 22/44.
  3. Привівши дроби до спільного знаменника, складіть або відніміть чисельники дробів, щоб отримати відповідь.
    • Додавання: 36 / 44 + 22 / 44 = (36 + 22) / 44 =58/44
    • Віднімання: 36 / 44 - 22/44 = (36 - 22) / 44 =14 / 44
  4. Перетворіть неправильну дріб в змішане число.неправильна дріб-це дріб, чисельник якої більше знаменника (тобто значення такого дробу більше 1). Для перетворення неправильної дробу в змішане число розділіть чисельник на знаменник. Наприклад, розглянемо дріб 58/44. 58 ÷ 44 = 1 із залишком 14. Таким чином, ви отримали змішане число 1 14/44.
    • Якщо ви не знаєте, якділити числа, віднімайте знаменник з чисельника. Наприклад, розглянемо дріб 317/100:
    • 317 - 100 = 217 (відняли 1 раз). 217 - 100 = 117 (відняли 2 рази). 117 - 100 = 17 (відняли 3 рази). Більше віднімати не можна, тому Відповідь: 3 17/100.
  5. Спростіть дріб.спрощення дробу-це скорочення чисельника і знаменника до мінімально можливих чисел. Для цього розділіть чисельник і знаменник на одне число. Якщо дріб можна ще спростити, зробіть це. Наприклад, розглянемо дріб 14/44.
    • 14 і 44 діляться на 2:
    • (14 ÷ 2)/(44 ÷ 2) =7/22
    • Так як немає числа, на яке ділиться і 7, і 22, то спрощена дріб дорівнює 7/22.

Приклади завдань

  • Спробуйте вирішити наступні завдання. Отримавши відповідь, виділіть невидимий текст після знаків рівності, щоб відкрити правильну відповідь і перевірити вашу роботу. Завдання ускладнюються в міру руху вниз. Останні завдання найскладніші, тому не засмучуйтеся, якщо не зможете вирішити їх з першого разу:

Додавання дробів:

  • 1 / 2 + 3 / 8 =7 / 8
  • 2 / 5 + 1 / 3 =11 / 15
  • 3 / 4 + 4 / 8 =1 1/4
  • 10 / 3 + 3 / 9 =3 2/3
  • 5 / 6 + 8 / 5 = 2 13/30
  • 2 / 17 + 4 / 5 = 78 / 85

Віднімання дробів:

  • 2 / 3 - 5 / 9 = 1 / 9
  • 15 / 20 - 3 / 5 = 3 / 20
  • 7 / 8 - 7 / 9 = 7 / 72
  • 3 / 5 - 4 / 7 = 1 / 35
  • 7 / 12 - 3 / 8 = 5 / 24
  • 16 / 5 - 1 / 4 = 2 19/20

Поради

  • Найменший спільний знаменник позначається як НОЗ.



Ще почитати: