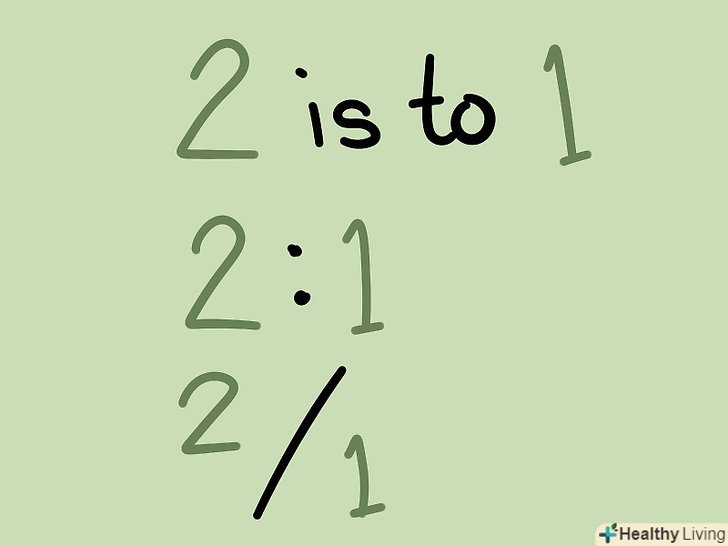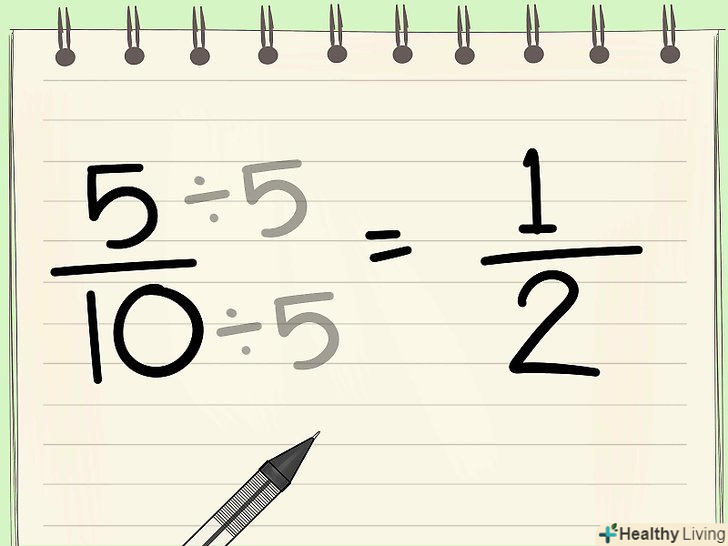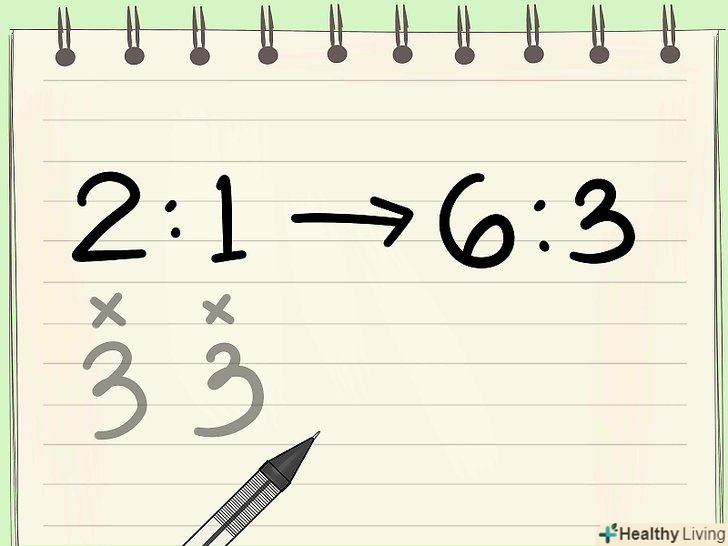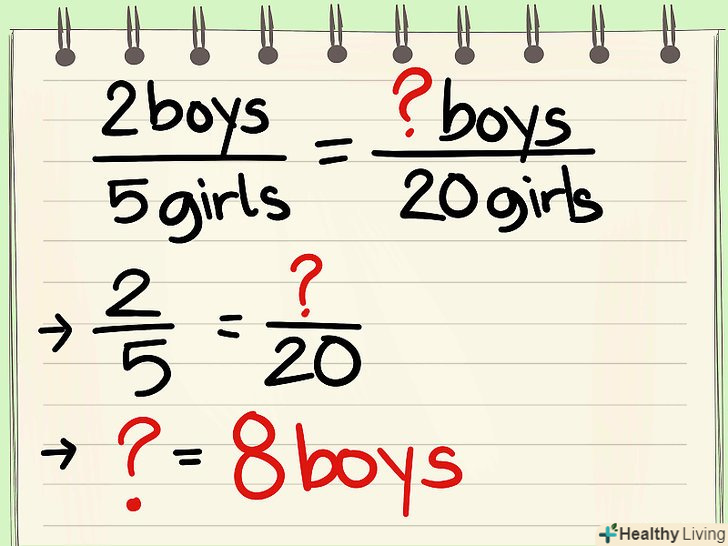1. Головна
    2. Математика
    3. Як робити GIF анімацію в Фотошопі: 6 кроків

Як робити GIF анімацію в Фотошопі: 6 кроків

Співвідношення – в математиці) - це взаємозв'язок між двома або більше числами одного роду. Співвідношення порівнюють абсолютні величини або частини цілого. Співвідношення обчислюються і записуються по-різному, але основні принципи однакові для всіх співвідношень.

Частина1 З 2:
Визначення співвідношень

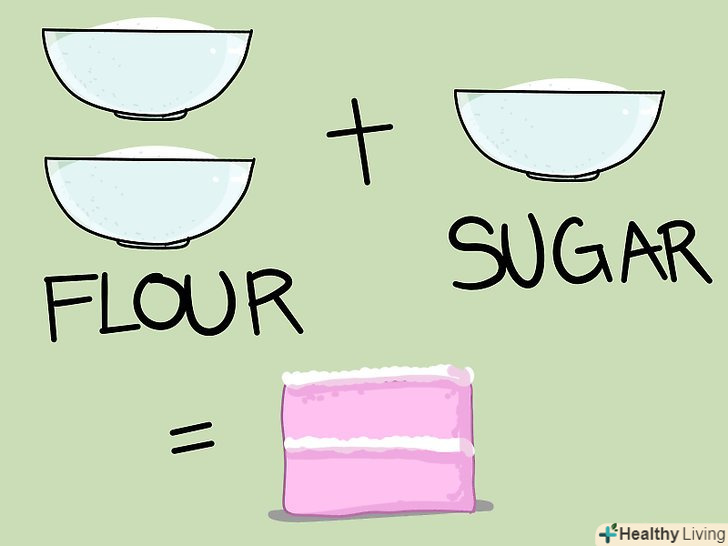
  1. Використання співвідношень.співвідношення використовуються як в науці, так і в повсякденному житті для порівняння величин. Найпростіші співвідношення пов'язують тільки два числа, але є співвідношення, що порівнюють три або більше значення. У будь-якій ситуації, в якій присутній більше однієї величини, можна записати співвідношення. Пов'язуючи деякі значення, співвідношення можуть, наприклад, підказати, як збільшити кількість інгредієнтів в рецепті або речовин в хімічній реакції.[1]
  2. Визначення співвідношень. співвідношення-це взаємозв'язок між двома (або більше) значеннями одного роду. Наприклад, якщо для приготування торта необхідні 2 склянки борошна і 1 склянка цукру, то співвідношення борошна до цукру одно 2 до 1.
    • Співвідношення можуть бути використані і в тих випадках, коли дві величини не пов'язані один з одним (як в прикладі з тортом). Наприклад, якщо в класі вчаться 5 дівчаток і 10 хлопчиків, то співвідношення дівчаток до хлопчиків одно 5 до 10. Ці величини (число хлопчиків і число дівчаток) не залежать один від одного, тобто їх значення зміняться, якщо хтось піде з класу або в клас прийде новий Учень/учениця. Співвідношення просто порівнюють значення величин.
  3. Зверніть увагу на різні способи представлення співвідношень.співвідношення можуть бути представлені словами або за допомогою математичних символів.[2]
    • Дуже часто співвідношення представляються словами (як показано вище). Особливо така форма уявлення співвідношень застосовується в повсякденному житті, далекій від науки.
    • Також співвідношення можна виразити через двокрапку. При порівнянні двох чисел в співвідношенні ви будете використовувати одну двокрапку (наприклад, 7:13); при порівнянні трьох і більше значень ставте двокрапка між кожною парою чисел (наприклад, 10:2:23). У нашому прикладі з класом ви можете висловити співвідношення дівчаток і хлопчиків так: 5 дівчаток: 10 хлопчиків. Або так: 5: 10.
    • Рідше співвідношення виражаються за допомогою похилої риси. У прикладі з класом воно може бути записано так: 5/10. Проте, це не дріб і читається таке співвідношення не як дріб; більш того, запам'ятайте, що в співвідношенні цифри не являють собою частину єдиного цілого.

Частина2 З 2:
Використання співвідношень

  1. Спростіть співвідношення. співвідношення можна спростити (аналогічно дробів), розділивши кожен член (число) співвідношення на найбільший спільний дільник. Однак при цьому не пропустіть з уваги вихідних значень співвідношення.[3]
    • У нашому прикладі в класі 5 дівчаток і 10 хлопчиків; співвідношення дорівнює 5:10. Найбільший спільний дільник членів співвідношення дорівнює 5 (так як і 5, і 10 діляться на 5). Розділіть кожне число співвідношення на 5 і отримаєте співвідношення 1 дівчинка до 2 хлопчиків (або 1:2). Однак при спрощенні співвідношення пам'ятайте про вихідні значення. У нашому прикладі в класі не 3 учні, а 15. Спрощене співвідношення порівнює кількість хлопчиків і кількість дівчаток. Тобто на кожну дівчинку припадає 2 хлопчика, але в класі не 2 хлопчика і 1 дівчинка.
    • Деякі співвідношення не спрощуються. Наприклад, співвідношення 3:56 не спрощується, так як у цих чисел немає спільних дільників (3 - просте число, а 56 не ділиться на 3).
  2. Використовуйте множення або ділення для збільшення або зменшення співвідношення. поширені завдання, в яких необхідно збільшити або зменшити два значення, пропорційних один одному. Якщо вам дано співвідношення і потрібно знайти відповідне йому більше або менше співвідношення, помножте або розділіть вихідне співвідношення на деяке дане число.[4]
    • Наприклад, Пекар повинен потроїти кількість інгредієнтів, даних в рецепті. Якщо за рецептом співвідношення борошна до цукру становить 2 до 1 (2:1), то Пекар помножить кожен член співвідношення на 3 і отримає співвідношення 6:3 (6 чашок борошна до 3 чашок цукру).
    • З іншого боку, якщо пекареві необхідно уполовинити кількість інгредієнтів, даних в рецепті, то Пекар розділить кожен член співвідношення на 2 і отримає співвідношення 1:½ (1 чашка борошна до 1/2 чашки цукру).
  3. Пошук невідомого значення, коли дані два еквівалентних співвідношення. це завдання, в якому необхідно знайти невідому змінну в одному співвідношенні за допомогою другого співвідношення, яке еквівалентно першому. Для вирішення таких завдань користуйтеся множенням хрест-навхрест. Запишіть кожне співвідношення у вигляді звичайного дробу, поставте між ними знак рівності і перемножте їх члени хрест-навхрест.[5]
    • Наприклад, дана група учнів, в якій 2 хлопчика і 5 дівчаток. Яке буде число хлопчиків, якщо число дівчаток збільшити до 20 (пропорція зберігається)? По-перше, запишіть два співвідношення - 2 хлопчика:5 дівчаток і Х хлопчиків:20 дівчаток. Тепер запишіть ці співвідношення у вигляді дробів: 2/5 і х/20. Перемножте члени дробів хрест-навхрест і отримаєте 5x = 40; отже, х = 40/5 = 8.

Джерела

  1. ↑ Http://www.virtualnerd.com/common-core/grade-6/6_RP-ratios-proportional-relationships/A
  2. ↑ Http://www.purplemath.com/modules/ratio.htm
  3. ↑ Http://www.helpwithfractions.com/math-homework-helper/least-common-denominator/
  4. ↑ Http://www.mathplanet.com/education/algebra-1/how-to-solve-linear-equations/ratios-and-proportions-and-how-to-solve-them
  5. ↑ Http://www.math.com/school/subject1/lessons/S1U2L2DP.html

Ще почитати: