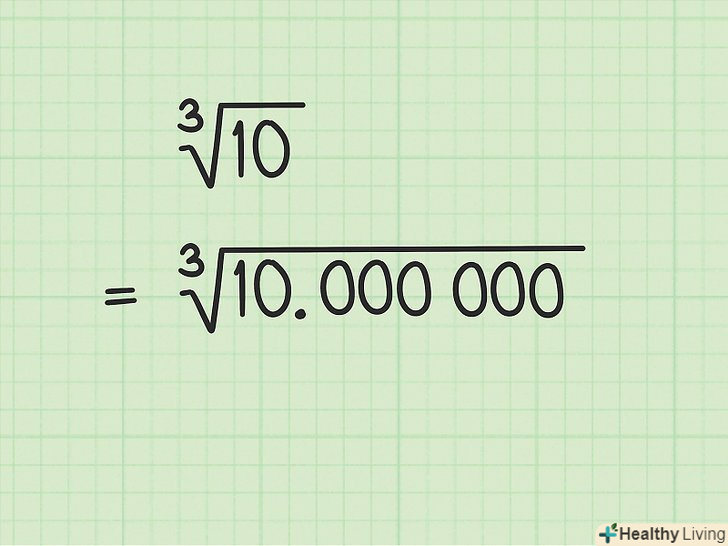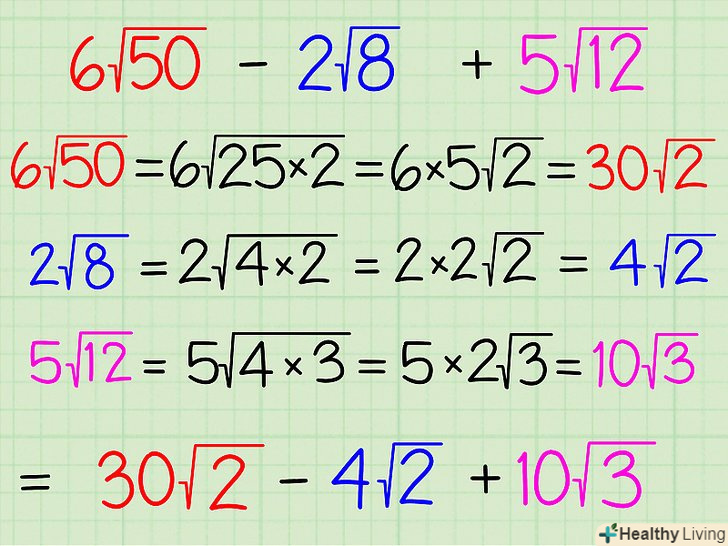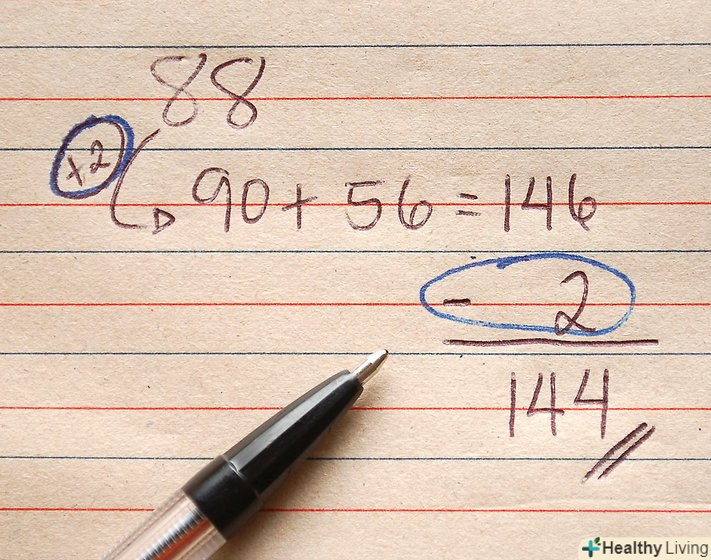Незважаючи на те, що завдання з математики можна вирішувати різними способами, існує загальний метод візуалізації, підходу і рішення, який дозволяє вирішувати навіть найскладніші завдання. Цей метод дозволяє також підвищити математичні знання та вміння. У статті розказано про способи вирішення ряду математичних задач.
Кроки
Частина1З 3:
Розуміння завдання
Частина1З 3:
 Визначте, до якого типу належить завдання.це арифметична задача? Дії з дробами? Рішення квадратних рівнянь? Перш ніж приступити до вирішення, з'ясуйте, до якої області математики відноситься завдання. Це важливо, оскільки значно спростить пошук способу вирішення.[1]
Визначте, до якого типу належить завдання.це арифметична задача? Дії з дробами? Рішення квадратних рівнянь? Перш ніж приступити до вирішення, з'ясуйте, до якої області математики відноситься завдання. Це важливо, оскільки значно спростить пошук способу вирішення.[1] Уважно прочитайте умову задачі.навіть якщо завдання здається простим, уважно вивчіть її умова. Не слід приступати до вирішення завдання, лише побіжно ознайомившись з її умовою. Якщо завдання складне, вам, можливо, знадобиться кілька разів перечитати її умова, щоб повністю зрозуміти його. Не шкодуйте часу на це і не приступайте до подальших дій до тих пір, поки не дізнаєтеся точно, що дано в умові і що необхідно знайти.[2][3]
Уважно прочитайте умову задачі.навіть якщо завдання здається простим, уважно вивчіть її умова. Не слід приступати до вирішення завдання, лише побіжно ознайомившись з її умовою. Якщо завдання складне, вам, можливо, знадобиться кілька разів перечитати її умова, щоб повністю зрозуміти його. Не шкодуйте часу на це і не приступайте до подальших дій до тих пір, поки не дізнаєтеся точно, що дано в умові і що необхідно знайти.[2][3] Викладіть умову задачі.для кращого розуміння завдання корисно викласти її умова своїми словами. Можна просто переказати умова, або записати його в тому випадку, якщо вам незручно говорити вголос (наприклад, на іспиті). Порівняйте власне виклад завдання з її початковою умовою, з'ясувавши тим самим, чи правильно ви зрозуміли завдання.[4][5]
Викладіть умову задачі.для кращого розуміння завдання корисно викласти її умова своїми словами. Можна просто переказати умова, або записати його в тому випадку, якщо вам незручно говорити вголос (наприклад, на іспиті). Порівняйте власне виклад завдання з її початковою умовою, з'ясувавши тим самим, чи правильно ви зрозуміли завдання.[4][5] Зобразіть задачу графічно.якщо ви вважаєте, що це допоможе, уявіть завдання графічно — можливо, так легше буде визначити подальші дії. Необов'язково створювати детальну схему, досить накидати умова завдання в загальних рисах, вказавши чисельні значення. При створенні схеми справляйтеся з умовою завдання, після закінчення Порівняйте готове зображення з умовою ще раз. Задайте самому собі питання: "чи вірно мій малюнок відображає завдання?"Якщо так, можна приступити до вирішення завдання. Якщо ж відповідь негативна, перечитайте умова ще раз.[6][7]
Зобразіть задачу графічно.якщо ви вважаєте, що це допоможе, уявіть завдання графічно — можливо, так легше буде визначити подальші дії. Необов'язково створювати детальну схему, досить накидати умова завдання в загальних рисах, вказавши чисельні значення. При створенні схеми справляйтеся з умовою завдання, після закінчення Порівняйте готове зображення з умовою ще раз. Задайте самому собі питання: "чи вірно мій малюнок відображає завдання?"Якщо так, можна приступити до вирішення завдання. Якщо ж відповідь негативна, перечитайте умова ще раз.[6][7]- Побудуйте діаграму Венна. Ця діаграма зображує співвідношення між величинами, що фігурують в задачі. Діаграма Венна особливо корисна при вирішенні арифметичних задач.[8]
- Побудуйте графік або діаграму.[9]
- Розташуйте наведені в умові величини уздовж прямої лінії.[10]
- Щоб представити більш складні об'єкти, використовуйте прості геометричні фігури.[11]
 Вивчіть структуру завдання. уважно прочитавши умова, ви, можливо, згадаєте схожі завдання, вирішені вами раніше. Можна побудувати таблицю з внесеними в неї даними, яка допоможе вам визначити характер завдання. Відзначте виявлені характерні риси завдання - вони допоможуть вам при її вирішенні. Не виключено навіть, що ви згадаєте схожі завдання і відразу отримаєте відповідь.[12]
Вивчіть структуру завдання. уважно прочитавши умова, ви, можливо, згадаєте схожі завдання, вирішені вами раніше. Можна побудувати таблицю з внесеними в неї даними, яка допоможе вам визначити характер завдання. Відзначте виявлені характерні риси завдання - вони допоможуть вам при її вирішенні. Не виключено навіть, що ви згадаєте схожі завдання і відразу отримаєте відповідь.[12] Вивчіть зроблені позначки.ще раз перевірте свої записи, переконавшись, що ви не помилилися в числах і інших даних. Не приступайте до складання плану рішення до тих пір, поки не будете впевнені в тому, що володієте всією необхідною інформацією і повністю розумієте завдання. Якщо ви не до кінця зрозуміли завдання, вивчіть схожі приклади в підручнику або в Інтернеті. Ознайомлення зі схожими завданнями, вирішеними іншими людьми, допоможе вам зрозуміти, що потрібно зробити для вирішення завдання, яку вирішуєте ви.
Вивчіть зроблені позначки.ще раз перевірте свої записи, переконавшись, що ви не помилилися в числах і інших даних. Не приступайте до складання плану рішення до тих пір, поки не будете впевнені в тому, що володієте всією необхідною інформацією і повністю розумієте завдання. Якщо ви не до кінця зрозуміли завдання, вивчіть схожі приклади в підручнику або в Інтернеті. Ознайомлення зі схожими завданнями, вирішеними іншими людьми, допоможе вам зрозуміти, що потрібно зробити для вирішення завдання, яку вирішуєте ви.
Частина2З 3:
Складання плану рішення
Частина2З 3:
 З'ясуйте, які формули знадобляться для вирішення завдання.якщо завдання досить складне, може знадобитися кілька формул. Ознайомтеся з необхідним для вирішення матеріалом в підручнику.[13]
З'ясуйте, які формули знадобляться для вирішення завдання.якщо завдання досить складне, може знадобитися кілька формул. Ознайомтеся з необхідним для вирішення матеріалом в підручнику.[13] Випишіть те, що може знадобитися при розв'язанні задачі.складіть послідовний список кроків, які необхідно зробити, щоб отримати відповідь. Це допоможе вам правильно організувати свою роботу і зосередитися на вирішенні завдання. Правильно складений план допоможе також приблизно оцінити відповідь заздалегідь, перш ніж ви вирішите завдання.[14][15]
Випишіть те, що може знадобитися при розв'язанні задачі.складіть послідовний список кроків, які необхідно зробити, щоб отримати відповідь. Це допоможе вам правильно організувати свою роботу і зосередитися на вирішенні завдання. Правильно складений план допоможе також приблизно оцінити відповідь заздалегідь, перш ніж ви вирішите завдання.[14][15]

Частина3З 3:
Рішення задачі
Частина3З 3:
 Дотримуйтеся складеного плану.виконуйте етапи послідовно в тому порядку, в якому ви намітили їх раніше. Щоб уникнути помилок, перевіряйте результат, отриманий на кожному етапі.[20]
Дотримуйтеся складеного плану.виконуйте етапи послідовно в тому порядку, в якому ви намітили їх раніше. Щоб уникнути помилок, перевіряйте результат, отриманий на кожному етапі.[20] Порівнюйте отримані результати з попередньо зробленими оцінками.по завершенні кожного етапу корисно порівняти його результат зі зробленими раніше оцінками; зіставте також кінцеву відповідь з його попередньою оцінкою. Задайте собі питання: "чи близькі мої припущення до отриманих результатів?"Якщо відповідь негативна, подумайте, чому. Перевірте отримані результати, переглянувши всі кроки рішення ще раз.[21]
Порівнюйте отримані результати з попередньо зробленими оцінками.по завершенні кожного етапу корисно порівняти його результат зі зробленими раніше оцінками; зіставте також кінцеву відповідь з його попередньою оцінкою. Задайте собі питання: "чи близькі мої припущення до отриманих результатів?"Якщо відповідь негативна, подумайте, чому. Перевірте отримані результати, переглянувши всі кроки рішення ще раз.[21] Спробуйте іншу схему вирішення.якщо складений вами план не спрацював, поверніться до етапу планування і розробіть новий план. Не турбуйтеся в разі невдалої спроби, навчання не обходиться без помилок-навпаки, ви навчитеся на своїх помилках і зможете уникнути їх надалі. Виявіть зроблені помилки і продовжуйте роботу. Не зациклюйтеся на помилках і не засмучуйтеся через них.[22]
Спробуйте іншу схему вирішення.якщо складений вами план не спрацював, поверніться до етапу планування і розробіть новий план. Не турбуйтеся в разі невдалої спроби, навчання не обходиться без помилок-навпаки, ви навчитеся на своїх помилках і зможете уникнути їх надалі. Виявіть зроблені помилки і продовжуйте роботу. Не зациклюйтеся на помилках і не засмучуйтеся через них.[22] Проаналізуйте завдання.отримавши правильну відповідь, поверніться до початку і перегляньте рішення ще раз. Аналіз завдання та її вирішення допоможе вам наступного разу, коли ви зіткнетеся з подібним завданням. Також ви краще засвоїте використані методи і прийоми, які обов'язково знадобляться вам надалі.[23]
Проаналізуйте завдання.отримавши правильну відповідь, поверніться до початку і перегляньте рішення ще раз. Аналіз завдання та її вирішення допоможе вам наступного разу, коли ви зіткнетеся з подібним завданням. Також ви краще засвоїте використані методи і прийоми, які обов'язково знадобляться вам надалі.[23]
Поради
- Якщо ви безуспішно випробували цілий ряд варіантів і не в змозі просунутися далі у вирішенні завдання, зверніться за допомогою до вчителя або репетитора. Він виявить допущені вами помилки і допоможе їх виправити.
- Продовжуйте використовувати діаграми та арифметичні дії. Регулярно переглядайте замітки, зроблені на заняттях. Для полегшення розуміння записуйте використовувані методи своїми словами і застосовуйте їх у міру необхідності.
Джерела
- ↑ Http://floridarti.usf.edu/resources/format/pdf/Classroom Cognitive and Metacognitive Strategies for Teachers_Revised_SR_09.08.10.pdf
- ↑ Http://www.interventioncentral.org/academic-interventions/math/math-problem-solving-combining-cognitive-metacognitive-strategies
- ↑ Http://floridarti.usf.edu/resources/format/pdf/Classroom Cognitive and Metacognitive Strategies for Teachers_Revised_SR_09.08.10.pdf
- ↑ Http://www.interventioncentral.org/academic-interventions/math/math-problem-solving-combining-cognitive-metacognitive-strategies
- ↑ Http://floridarti.usf.edu/resources/format/pdf/Classroom Cognitive and Metacognitive Strategies for Teachers_Revised_SR_09.08.10.pdf
- ↑ Http://www.interventioncentral.org/academic-interventions/math/math-problem-solving-combining-cognitive-metacognitive-strategies
- ↑ Http://floridarti.usf.edu/resources/format/pdf/Classroom Cognitive and Metacognitive Strategies for Teachers_Revised_SR_09.08.10.pdf
- ↑ Http://floridarti.usf.edu/resources/format/pdf/Classroom Cognitive and Metacognitive Strategies for Teachers_Revised_SR_09.08.10.pdf
- ↑ Http://floridarti.usf.edu/resources/format/pdf/Classroom Cognitive and Metacognitive Strategies for Teachers_Revised_SR_09.08.10.pdf
- ↑ Http://floridarti.usf.edu/resources/format/pdf/Classroom Cognitive and Metacognitive Strategies for Teachers_Revised_SR_09.08.10.pdf
- ↑ Http://floridarti.usf.edu/resources/format/pdf/Classroom Cognitive and Metacognitive Strategies for Teachers_Revised_SR_09.08.10.pdf
- ↑ Http://floridarti.usf.edu/resources/format/pdf/Classroom Cognitive and Metacognitive Strategies for Teachers_Revised_SR_09.08.10.pdf
- ↑ Http://tutorial.math.lamar.edu/Extras/StudyMath/ProblemSolving.aspx
- ↑ Http://tutorial.math.lamar.edu/Extras/StudyMath/ProblemSolving.aspx
- ↑ Https://math.berkeley.edu/~gmelvin/polya.pdf
- ↑ Http://tutorial.math.lamar.edu/Extras/StudyMath/ProblemSolving.aspx
- ↑ Https://math.berkeley.edu/~gmelvin/polya.pdf
- ↑ Http://www.interventioncentral.org/academic-interventions/math/math-problem-solving-combining-cognitive-metacognitive-strategies
- ↑ Http://floridarti.usf.edu/resources/format/pdf/Classroom Cognitive and Metacognitive Strategies for Teachers_Revised_SR_09.08.10.pdf
- ↑ Http://floridarti.usf.edu/resources/format/pdf/Classroom Cognitive and Metacognitive Strategies for Teachers_Revised_SR_09.08.10.pdf
- ↑ Http://www.interventioncentral.org/academic-interventions/math/math-problem-solving-combining-cognitive-metacognitive-strategies
- ↑ Http://floridarti.usf.edu/resources/format/pdf/Classroom Cognitive and Metacognitive Strategies for Teachers_Revised_SR_09.08.10.pdf
- ↑ Http://floridarti.usf.edu/resources/format/pdf/Classroom Cognitive and Metacognitive Strategies for Teachers_Revised_SR_09.08.10.pdf