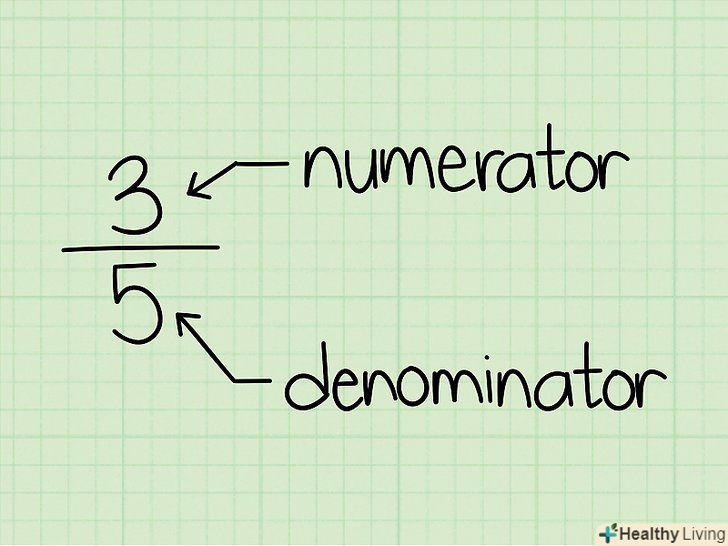
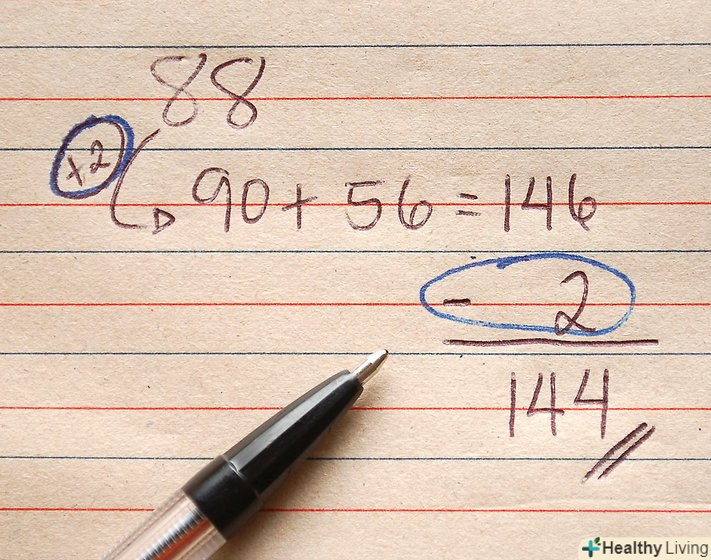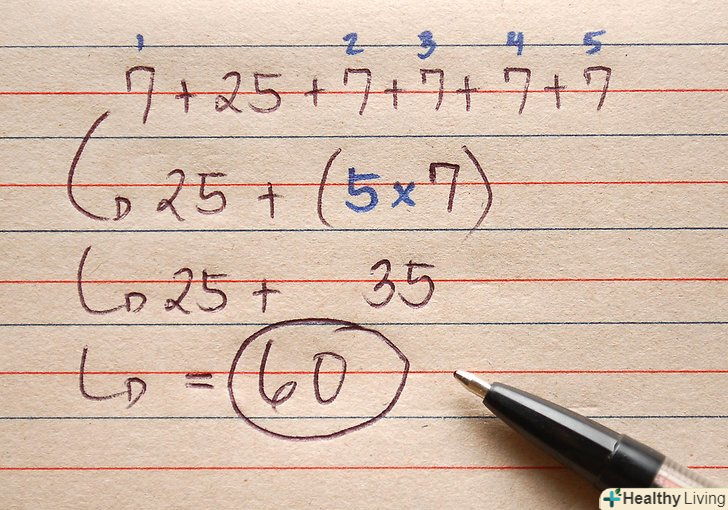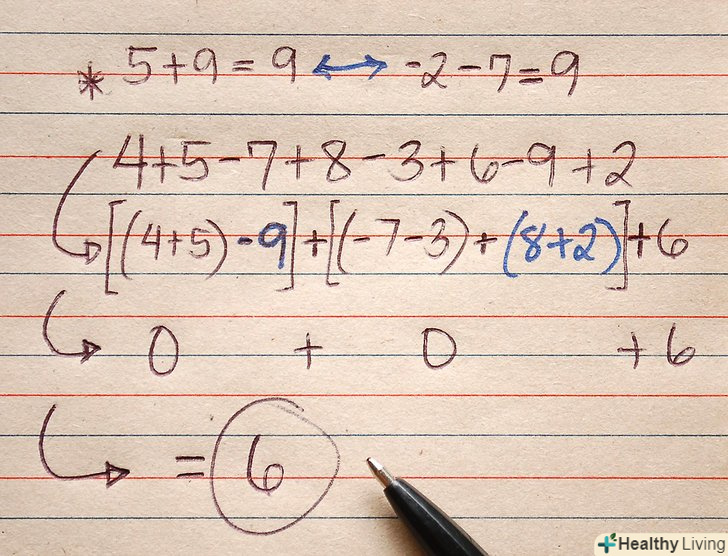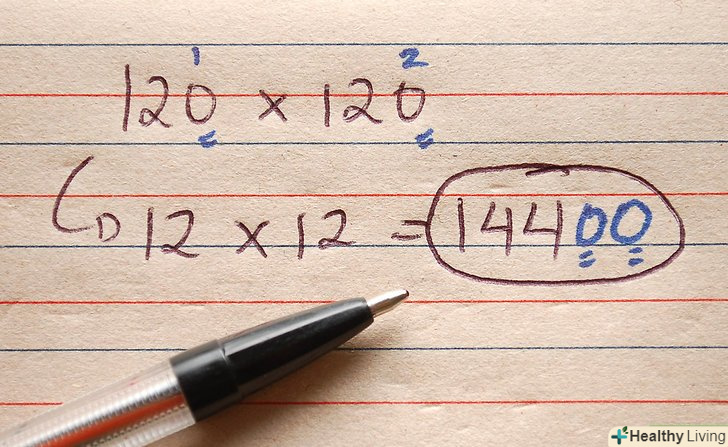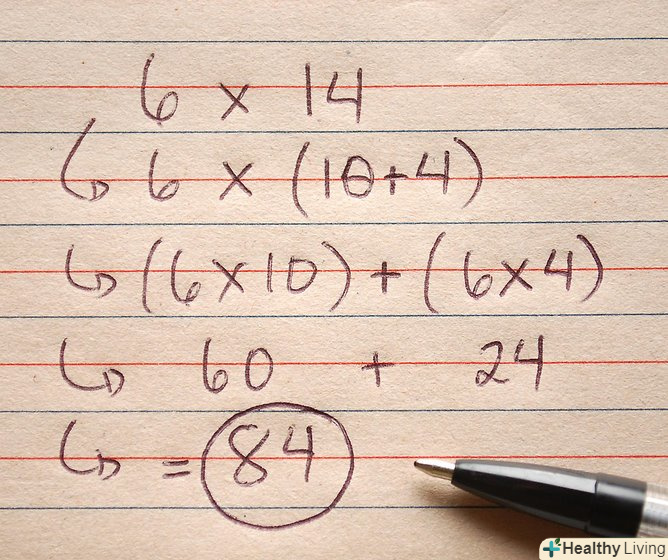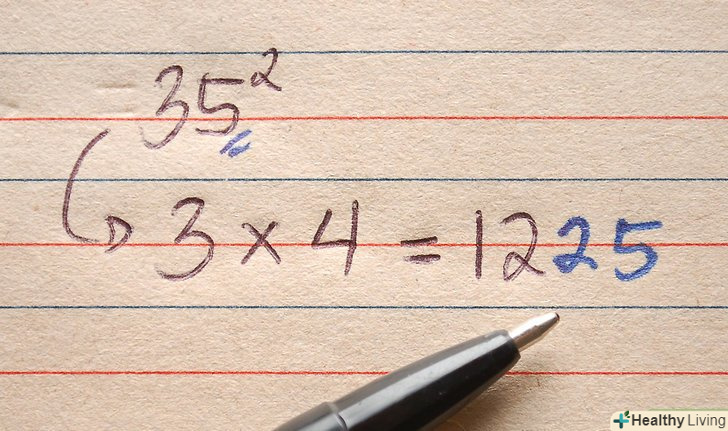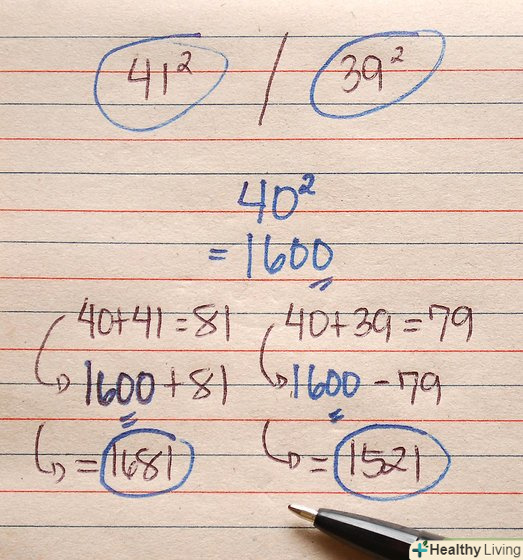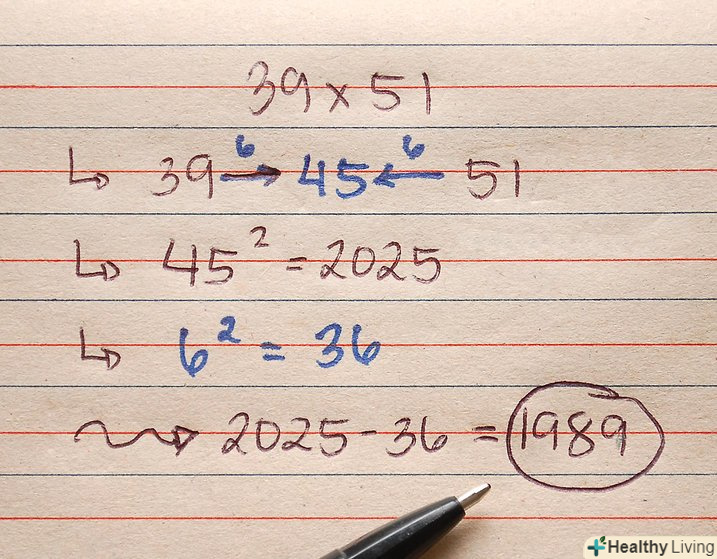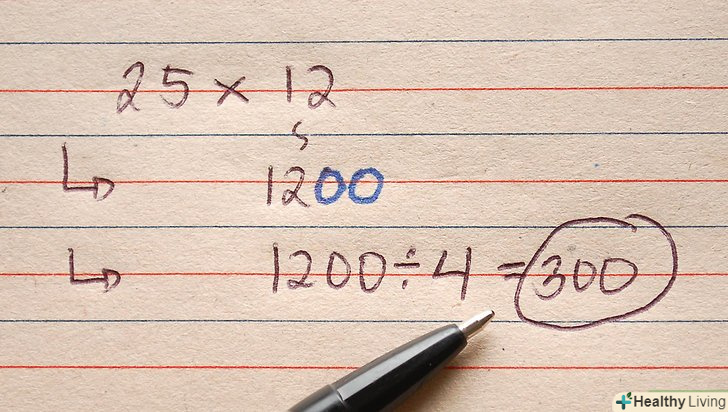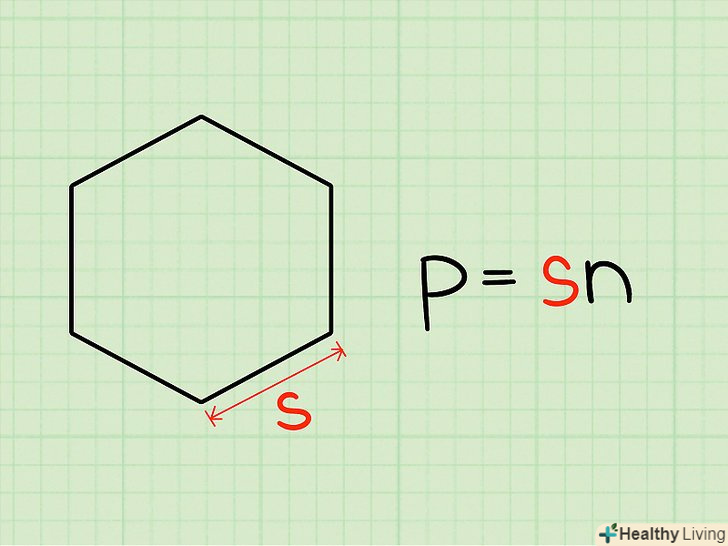1. Головна
    2. Математика
    3. Як робити обчислення в розумі-

Як робити обчислення в розумі-

Ця стаття розповість вам, як робити обчислення в розумі. Примітка: Ви повинні знати основи операцій додавання, віднімання, множення і ділення.

Метод1 З 2:
Додавання і віднімання

  1. Перетворіть число.
    1. Округліть число до десятків.
    2. Додайте до нього інше число.
    3. З результату відніміть / додайте число, яке ви додали / відняли для округлення вихідного числа.
      • Приклад 88 + 56 = ?; Округліть 88 до 90. Складіть 90 і 56 і отримаєте 146. З 146 відніміть 2 (2 + 88 = 90). Отже: 146 - 2 = 144.
      • Цей процес можна записати так: 56 + (90 -2). Інші приклади: 99 = (100 - 1); 68 = (70 - 2)
      • Ви можете використовувати аналогічну техніку для віднімання чисел.
  2. Перетворіть додавання декількох однакових чисел в множення.
    1. Зверніть увагу на те, скільки разів складається одне і те ж число.
      • Наприклад: 7 + 25 + 7 + 7 + 7 + 7 = 25 + (5 × 7) = 25 + 35 = 60.
  3. Пам'ятайте, що результат додавання / віднімання однакових чисел з протилежними знаками дорівнює 0, наприклад 7-7 = 0 або 5 - 2 + 4 – 7 = 0.
    1. Шукайте числа, результат додавання або віднімання яких дорівнює 0. (Примітка: малюнок, наведений вище, неправильний. Замість 5 + 9 = 9 &#lt;-&#gt; -2 -7 = 9 потрібно записати 5 + 4 = 9 &#lt;-&#gt; -2 -7 = -9) наприклад, 5 + 4 = 9 і -2 -7 = -9, тому 9 – 9 = 0. Таким чином, ви можете взагалі не враховувати ці чотири числа, так як результат операцій з ними дорівнює 0.
      • Наприклад:

        4 + 5 - 7 + 8 - 3 + 6 - 9 + 2 =

        (4 + 5) - 9 + ( -7 - 3) + (8 + 2) + 6 =

        0 + 0 + 6 = 6

Метод2 З 2:
Множення

  1. Множення чисел, що закінчуються на 0 (нуль). наприклад: 120х120 = ?
    1. Підрахуйте загальне число нулів, на які закінчуються числа (в нашому прикладі два нуля).
    2. Відкиньте нулі і продовжуйте обчислення. 12 × 12 = 144.
    3. Припишіть нулі праворуч від результату: 14400.
  2. Для перемноження складних чисел розкладіть їх на доданки, які простіше перемножити. Потім використовуйте наведені нижче методи.
    • Наприклад: 14 х 6 = ? Розкладіть 14 на 10 + 4, помножте кожен доданок на 6, а потім складіть результати. 14 × 6 = 6 × (10 + 4) = (10 × 6) + (4 × 6) = 60 + 24 = 84.
    • Наприклад: 35 * 37 = ? Зробіть наступне: 35 × (35 + 2) = 352 + (2 × 35) = 1225 + 70 = 1295.
  3. Зведіть в квадрат числа, що закінчуються на 5 (п'ять). наприклад: 352 = ?
    1. Ігноруйте 5 на кінці числа, а цифру перед п'ятіркою (в нашому прикладі 3) помножте на цифру, яка більше неї на 1 (в нашому прикладі 4): 3х4 = 12.
    2. До результату припишіть 25 (праворуч): 1225.
  4. Зведіть в квадрат числа, які на одиницю більше або менше числа, квадрат якого Ви знаєте. наприклад: 412 = ? або 392 = ?
    1. Згадайте квадрат числа, який Ви знаєте. 402 = 1600.
    2. Якщо вихідне число більше числа, квадрат якого Ви знаєте, то додавайте. В іншому випадку віднімайте.
    3. Складіть вихідне число і число, квадрат якого Ви знаєте. 40 + 41 = 81. 40 + 39 = 79.
    4. Складіть або відніміть. 1600 + 81 = 1681 ---&#gt; 412 = 1681

      1600 - 79 = 1521 ----&#gt; 392 = 1521
    • Цей метод вірний тільки для чисел, які на одиницю більше або менше числа, квадрат якого Ви знаєте.
  5. Спростіть операцію множення за допомогою різниці квадратів. наприклад: 39 х 51 = ?
    1. Знайдіть число, яке знаходиться на однаковій відстані від обох вихідних чисел. У нашому прикладі таким число є 45.
    2. Знайдене число зведіть в квадрат. 452 = 2025.
    3. Зведіть в квадрат різницю між знайденим числом і вихідним число. У нашому прикладі: 45 – 39 = 6 (або 51-45 = 6) і 62 = 36.
    4. Відніміть другий результат зведення в квадрат з першого. 2025 - 36 = 1989.
      • Перепишіть вираз так: 51 × 39 = (45 + 6) × (45 - 6) = 452 - 62
        ( x + y) X( x - y ) = x2 - y2
  6. Помножте на 25. наприклад: 25х12 =?
    1. Помножте число, відмінне від 25, на 100 (припишіть до цього числа два нуля праворуч). 12 × 100 = 1200.
    2. Розділіть результат на 4. 1200 ÷ 4 = 300. 25 × 12 = 300.

Ще почитати: