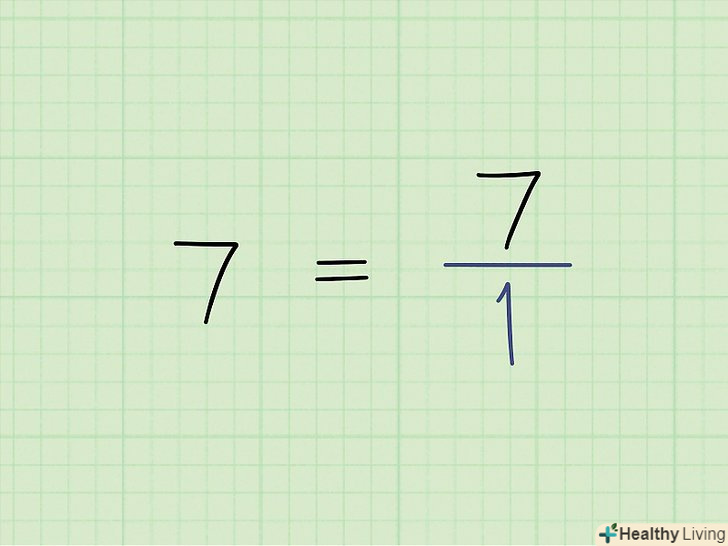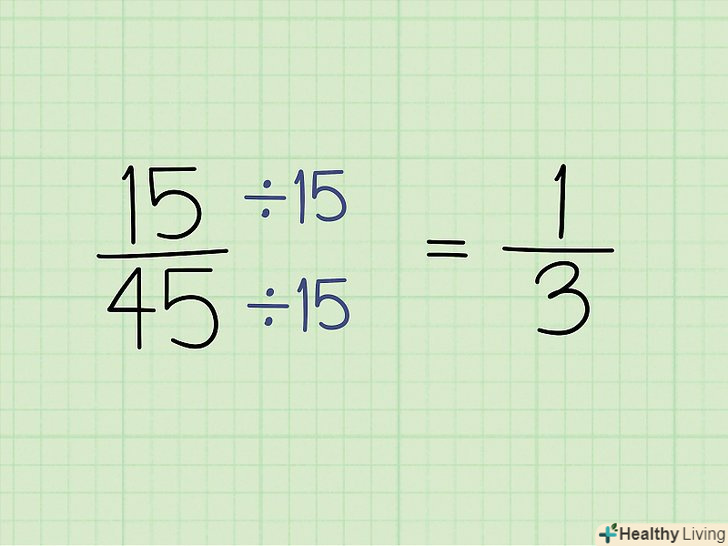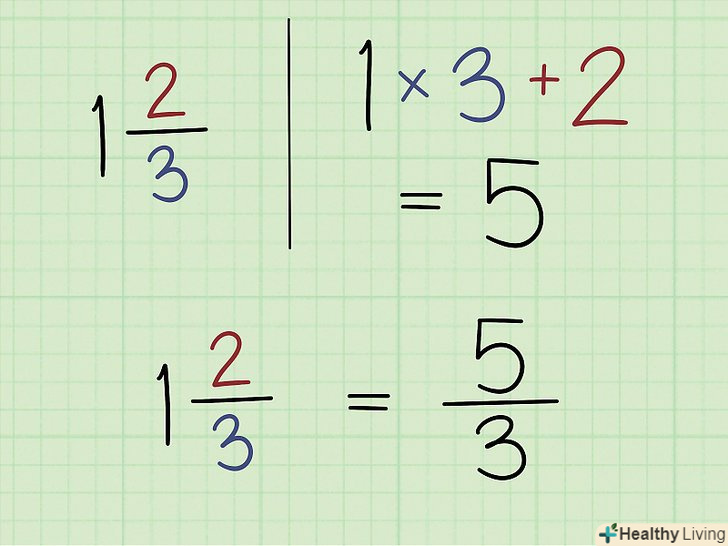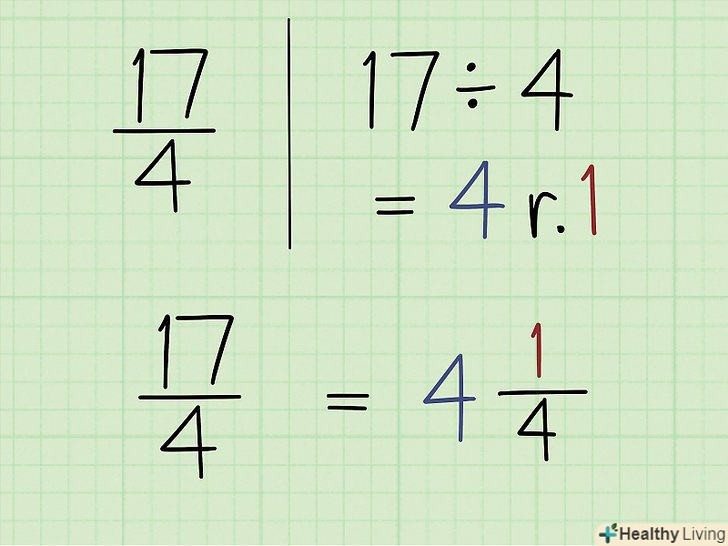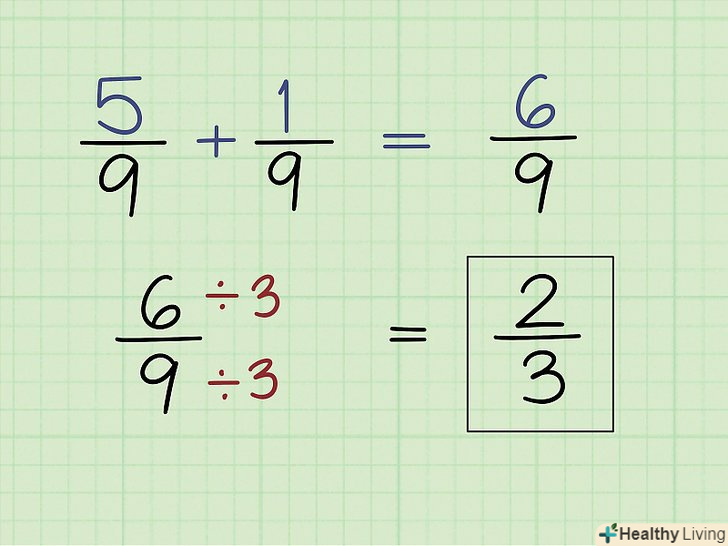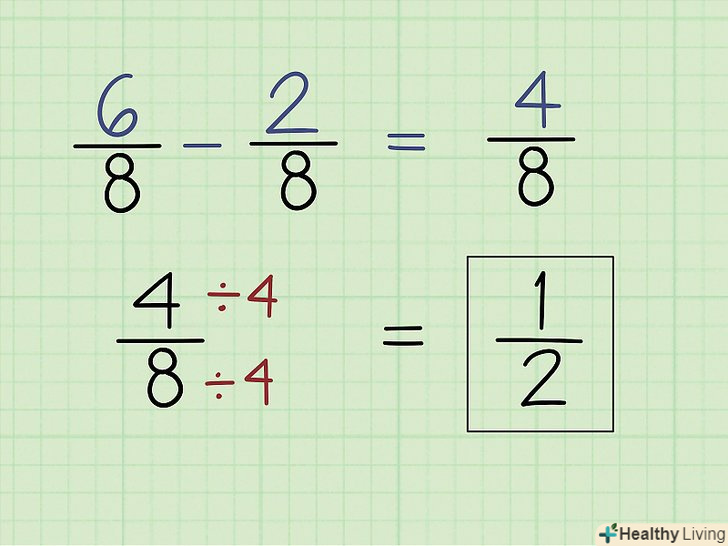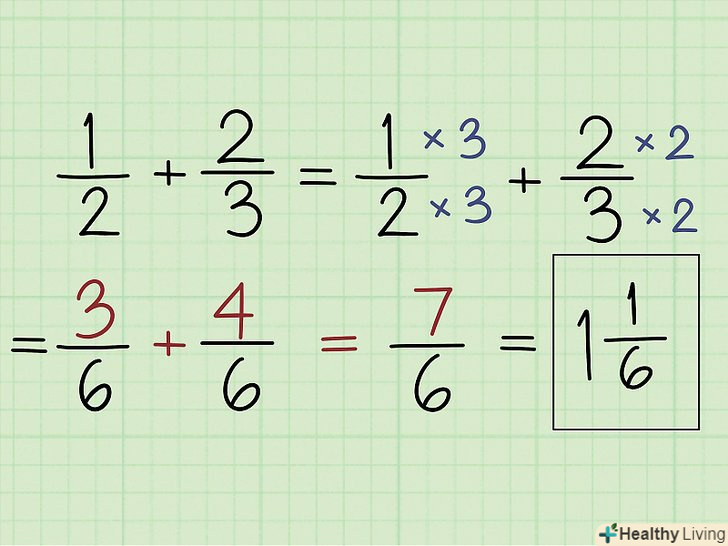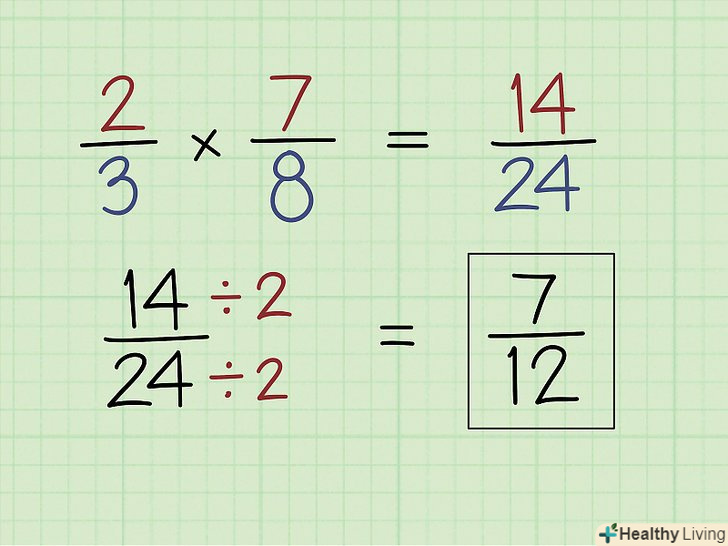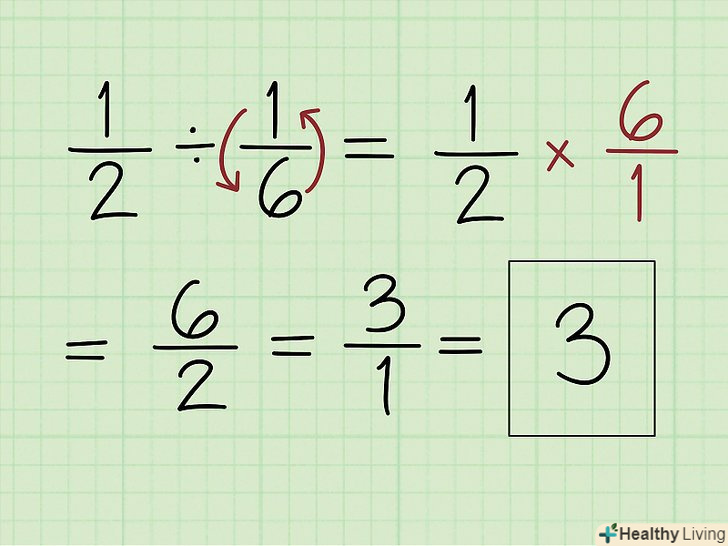Дії з дробами не такі складні, як здаються, особливо якщо знати, що робити. Почніть з вивчення термінології і основ, а потім перейдіть до додавання, віднімання, множення і ділення дробів. Як тільки ви зрозумієте, що таке дроби і як з ними працювати, ви будете швидко вирішувати вирази з дробами.
Кроки
Метод1 З 2:
Основні поняття
Метод1 З 2:
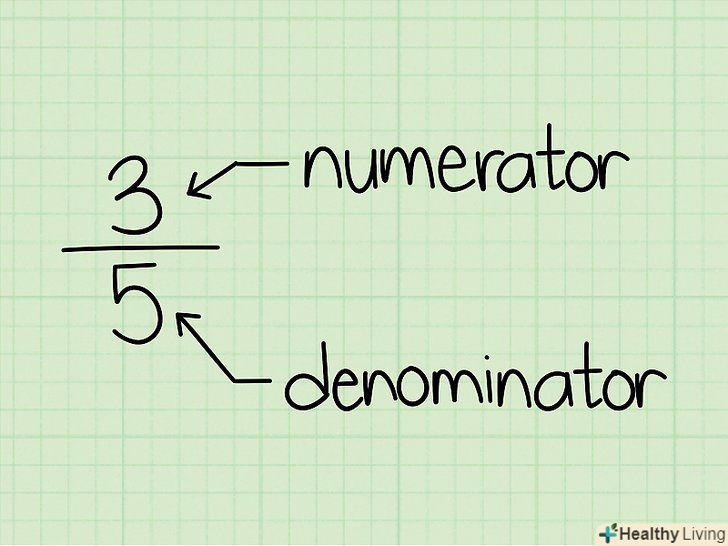
 Зверніть увагу, що чисельник знаходиться зверху, а знаменник — знизу.дріб-це частина цілого; верхнє число дробу називається чисельником і характеризує дану кількість частин цілого. Нижнє число дробу називається знаменником і вказує на кількість частин, які в сумі складають ціле.[1]
Зверніть увагу, що чисельник знаходиться зверху, а знаменник — знизу.дріб-це частина цілого; верхнє число дробу називається чисельником і характеризує дану кількість частин цілого. Нижнє число дробу називається знаменником і вказує на кількість частин, які в сумі складають ціле.[1]- Наприклад, дана дріб 3/5. Тут 3 — це чисельник (тобто дані 3 частини цілого), а 5-це знаменник (тобто ціле розділене на 5 частин). Інший приклад: дріб 7/8. Тут 7-чисельник, а 8 — знаменник.
 Перетворіть ціле число в дріб, записавши під ним 1.якщо дано ціле число, яке потрібно перетворити в дріб, запишіть це число в чисельнику, а в знаменнику запишіть 1.[2]
Перетворіть ціле число в дріб, записавши під ним 1.якщо дано ціле число, яке потрібно перетворити в дріб, запишіть це число в чисельнику, а в знаменнику запишіть 1.[2]- Наприклад, щоб перетворити 7 в дріб, запишіть 7/1.
 Спростіть дріб. для цього знайдіть найбільший спільний дільник (НСД) чисельника і знаменника. НСД - це найбільше число, на яке можна розділити і чисельник, і знаменник. Потім просто розділіть чисельник і знаменник на НОД, щоб спростити дріб.[3]
Спростіть дріб. для цього знайдіть найбільший спільний дільник (НСД) чисельника і знаменника. НСД - це найбільше число, на яке можна розділити і чисельник, і знаменник. Потім просто розділіть чисельник і знаменник на НОД, щоб спростити дріб.[3]- Наприклад, дана дріб 15/45. Тут НСД = 15, оскільки і 15, і 45 діляться на 15. Розділіть: 15/15 = 1-це новий чисельник; 45/15 = 3 — це новий знаменник. Таким чином, дріб 15/45 спрощується до 1/3.
 Навчіться перетворювати змішані числа в неправильні дроби. змішане число включає ціле число і дріб. Щоб полегшити вирішення деяких виразів з дробами, Перетворіть змішане число в неправильну дріб (в такий дробу чисельник більше знаменника). Для цього помножте ціле число на знаменник і до отриманого результату додайте чисельник. Тепер запишіть отримане число в чисельнику, а знаменник залиште колишнім.[4]
Навчіться перетворювати змішані числа в неправильні дроби. змішане число включає ціле число і дріб. Щоб полегшити вирішення деяких виразів з дробами, Перетворіть змішане число в неправильну дріб (в такий дробу чисельник більше знаменника). Для цього помножте ціле число на знаменник і до отриманого результату додайте чисельник. Тепер запишіть отримане число в чисельнику, а знаменник залиште колишнім.[4]- Наприклад, дано змішане число 1 2/3. Помножте 3 на 1 і отримаєте 3. Додайте 3 до 2 і отримаєте 5 (це новий чисельник). Таким чином, 1 2/3 = 5/3.
Порада: Перетворіть змішані числа в неправильні дроби, якщо ви їх множите або ділите.
 Навчіться перетворюватиНеправильні дроби в змішані числа.у деяких завданнях неправильну дріб потрібно перетворити в змішане число. Для цього розділіть чисельник на знаменник — цілочисельний результат ділення перетвориться в цілу частину змішаного числа, а залишок — в чисельник дробової частини (при цьому знаменник не зміниться). Щоб знайти залишок, помножте ціле число на дільник (знаменник) і результат відніміть з діленого (чисельника). [5]
Навчіться перетворюватиНеправильні дроби в змішані числа.у деяких завданнях неправильну дріб потрібно перетворити в змішане число. Для цього розділіть чисельник на знаменник — цілочисельний результат ділення перетвориться в цілу частину змішаного числа, а залишок — в чисельник дробової частини (при цьому знаменник не зміниться). Щоб знайти залишок, помножте ціле число на дільник (знаменник) і результат відніміть з діленого (чисельника). [5]- Наприклад, дана неправильна дріб 17/4. Розділіть: 17 ÷ 4 = 4 Ост.1 (щоб знайти залишок, помножте 4 * 4 = 16, а потім відніміть 17 – 16 = 1). Таким чином, 17/4 = 4 1/4.
Метод2 З 2:
Операції з дробами
Метод2 З 2:
 Складіть дробиІз загальним знаменником.для цього просто складіть їх чисельники. Запам'ятайте: складати можна тільки дроби з однаковим знаменником.[6]
Складіть дробиІз загальним знаменником.для цього просто складіть їх чисельники. Запам'ятайте: складати можна тільки дроби з однаковим знаменником.[6]- Наприклад, дано вираз 5/9 + 1/9. Тут просто складіть чисельники 5 + 1 = 6. Таким чином, 5/9 + 1/9 = 6/9 = 2/3.
 Відніміть дробиІз загальним знаменником.для цього просто відніміть менший чисельник з більшого. Запам'ятайте: віднімати (як і складати) можна тільки дробу з однаковим знаменником.[7]
Відніміть дробиІз загальним знаменником.для цього просто відніміть менший чисельник з більшого. Запам'ятайте: віднімати (як і складати) можна тільки дробу з однаковим знаменником.[7]- Наприклад, дано вираз 6/8-2/8. Тут відніміть 6 – 2 = 4. Таким чином, 6/8 - 2/8 = 4/8 = 1/2.
 Знайдіть загальний кратний , щоб скласти або відняти дроби з різними знаменниками.якщо у дробів різні знаменники, знайдіть спільне кратне обох знаменників і приведіть дробу до спільного знаменника. Для цього помножте чисельник і знаменник на деяке число, яке призводить дріб до спільного знаменника. Потім складіть або відніміть чисельники, щоб вирішити вираз.[8]
Знайдіть загальний кратний , щоб скласти або відняти дроби з різними знаменниками.якщо у дробів різні знаменники, знайдіть спільне кратне обох знаменників і приведіть дробу до спільного знаменника. Для цього помножте чисельник і знаменник на деяке число, яке призводить дріб до спільного знаменника. Потім складіть або відніміть чисельники, щоб вирішити вираз.[8]- Наприклад, дано вираз 1/2 + 2/3. Почніть з знаходження загального кратного. У нашому прикладі загальне кратне дорівнює 6, тому що 6 ділиться і на 2, і на 3. Щоб привести дріб 1/2 до знаменника 6, помножте чисельник і знаменник на 3: 1 x 3 = 3 і 2 х 3 = 6; вийде нова дріб 3/6. Щоб привести дріб 2/3 до знаменника 6, помножте чисельник і знаменник на 2: 2 x 2 = 4 і 3 x 2 = 6; вийде нова дріб 4/6. Тепер складіть чисельники: 3/6 + 4/6 = 7/6. Оскільки це неправильна дріб, її можна перетворити в змішане число 1 1/6.
- Інший приклад: 7/10-1/5. Тут загальним кратним є 10, тому що 10 ділиться на 10 і на 5. Щоб привести дріб 1/5 до знаменника 10, помножте чисельник і знаменник на 2: 1 x 2 = 2 і 5 x 2 = 10; вийде нова дріб 2/10. Зверніть увагу, що дріб 7/10 вже має спільний знаменник. Тепер відніміть чисельники: 7/10-2/10 = 5/10 = 1/2.
 Перемножте дроби.для цього просто перемножте їх чисельники, а потім перемножте їх знаменники. Якщо дріб або дроби можна спростити, зробіть це до множення.[9]
Перемножте дроби.для цього просто перемножте їх чисельники, а потім перемножте їх знаменники. Якщо дріб або дроби можна спростити, зробіть це до множення.[9]- Наприклад, дано вираз 2/3 * 7/8. Перемножте чисельники: 2 * 7 = 14. Потім перемножте знаменники: 3 * 8 = 24. Таким чином, 2/3 * 7/8 = 14/24 = 7/12 (якщо розділити чисельник і знаменник на 2).
 Розділіть дріб на дріб .для цього переверніть одну з дробів, а потім перемножте чисельники і перемножте знаменники. Тобто помножте дріб на зворотний дріб. Щоб знайти зворотний дріб, поміняйте місцями чисельник і знаменник. Тепер перемножте чисельники і перемножте знаменники.[10]
Розділіть дріб на дріб .для цього переверніть одну з дробів, а потім перемножте чисельники і перемножте знаменники. Тобто помножте дріб на зворотний дріб. Щоб знайти зворотний дріб, поміняйте місцями чисельник і знаменник. Тепер перемножте чисельники і перемножте знаменники.[10]- Наприклад, дано вираз 1/2 ÷ 1/6. Переверніть дріб 1/6 і отримайте 6/1. Тепер перемножте: 1 x 6 = 6 (це новий чисельник) і 2 x 1 = 2 (це новий знаменник). Отже, 1/2 ÷ 1/6 = 6/2 = 3.
Поради
- Уважно прочитайте завдання (принаймні двічі), щоб зрозуміти, що в ній потрібно знайти.
- Запитайте у вчителя, чи потрібно перетворювати неправильні дроби в змішані числа і / або спрощувати дроби.
- Щоб знайти зворотне значення цілого числа, запишіть це число під 1. Наприклад, 5 перетвориться на 1/5.
- Знаменника, який дорівнює нулю, не буває, тому що на 0 ділити не можна.
Джерела
- ↑ Https://medium.com/i-math/the-no-nonsense-straightforward-da76a4849ec
- ↑ Https://medium.com/i-math/the-no-nonsense-straightforward-da76a4849ec
- ↑ Http://www.math.com/school/subject1/lessons/S1U4L2GL.html
- ↑ Https://sciencing.com/solve-math-problems-fractions-7964895.html
- ↑ Https://sciencing.com/solve-math-problems-fractions-7964895.html
- ↑ Https://www.bbc.co.uk/bitesize/articles/z9n4k7h
- ↑ Https://www.bbc.co.uk/bitesize/articles/z9n4k7h
- ↑ Https://www.bbc.co.uk/bitesize/articles/z9n4k7h
- ↑ Http://www.math.com/school/subject1/lessons/S1U4L4GL.html