Уміння складати дробів-це дуже корисний навик, який стане в нагоді не тільки в школі, але і в повсякденному житті. У цій статті ми розповімо вам, як складати дроби.
Кроки
Частина1 З 2:
Як складати дроби з однаковими знаменниками
Частина1 З 2:
Подивіться на знаменники (числа під рисою) дробів. якщо вони однакові, вам дано дроби з однаковими (рівними) знаменниками; в іншому випадку перейдіть в наступний розділ.-
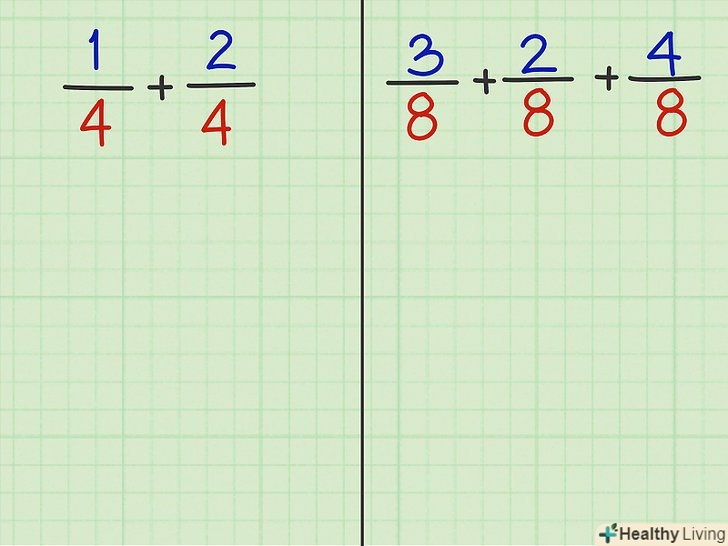
Розглянемо два приклади, на основі яких продемонструємо, як складати дроби з рівними знаменниками.
- Приклад 1: 1/4 + 2/4
- Приклад 2: 3/8 + 2/8 + 4/8
-
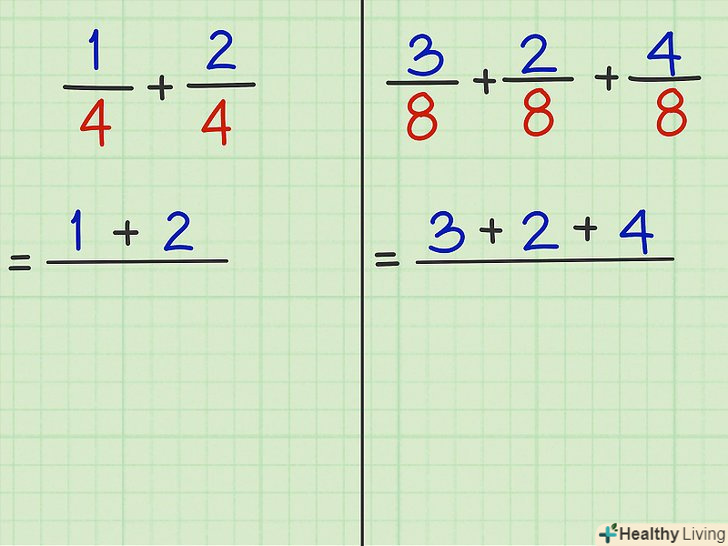
Складіть чисельники (числа над рисою). якщо знаменники дробів рівні, просто складіть чисельники.
- Приклад 1: 1/4 + 2/4. Тут числа " 1 " і " 2 " є чисельниками, тому 1 + 2 = 3.
- Приклад 2: 3/8 + 2/8 + 4/8. Тут числа "3" « " 2 " і " 4 " є чисельниками, тому 3 + 2 + 4 = 9.
-
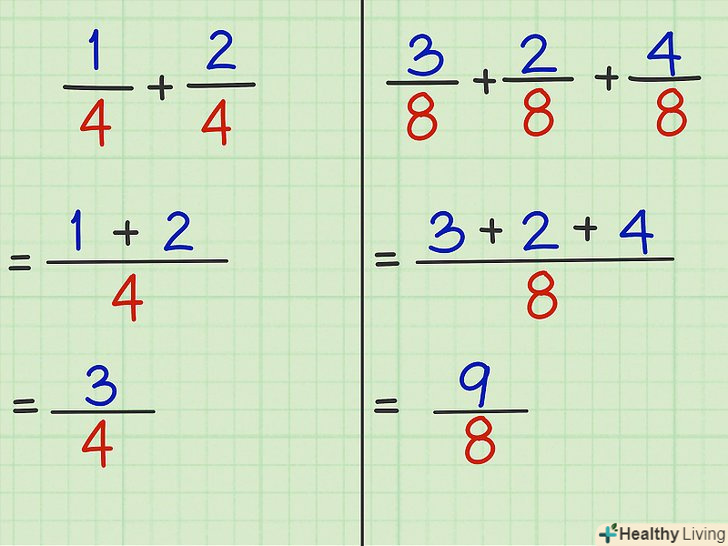
Запишіть кінцеву дріб.знайдену суму чисельників запишіть в чисельнику нового дробу. Тепер запишіть однаковий знаменник у знаменнику нового дробу, тобто вихідний знаменник не змінюється.
- Приклад 1: 3 — це чисельник, а 4-знаменник кінцевої дробу. Таким чином, 1/4 + 2/4 = 3/4.
- Приклад 2: 9 — це чисельник, а 8-знаменник кінцевої дробу. Таким чином, 3/8 + 2/8 + 4/8 = 9/8.
-
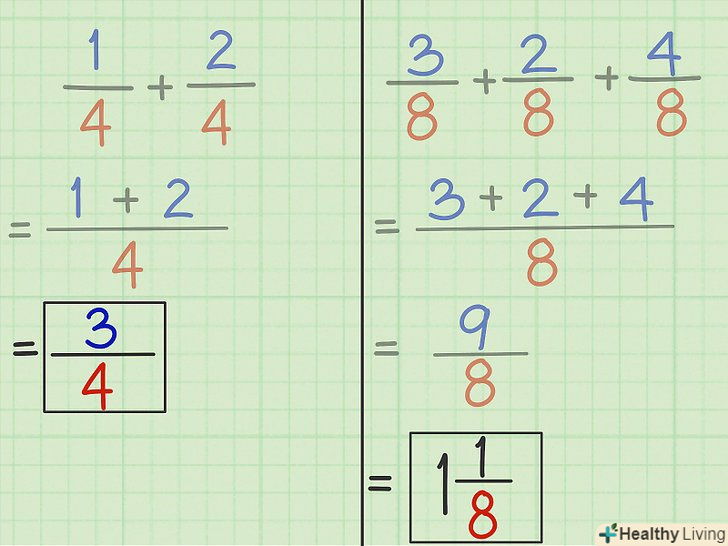
Спростіть кінцеву дріб (якщо потрібно).
- Якщо чисельник більший за знаменник (як у прикладі 2), Перетворіть такий неправильний дріб у змішане число. Для цього розділіть чисельник на знаменник. У нашому прикладі 9/8 = 1 і залишок 1. Тепер цілочисельний результат ділення запишіть перед Новим дробом, в її чисельнику запишіть залишок, а її знаменником буде знаменник вихідної дробу. Таким чином,
9/8 = 1 1/8.
- Якщо чисельник більший за знаменник (як у прикладі 2), Перетворіть такий неправильний дріб у змішане число. Для цього розділіть чисельник на знаменник. У нашому прикладі 9/8 = 1 і залишок 1. Тепер цілочисельний результат ділення запишіть перед Новим дробом, в її чисельнику запишіть залишок, а її знаменником буде знаменник вихідної дробу. Таким чином,
Частина2 З 2:
Як складати дроби з різними знаменниками
Частина2 З 2:
-
Подивіться на знаменники (числа під рисою) дробів. якщо вони відрізняються один від одного, вам дано дроби з різними знаменниками. В цьому випадку дробу потрібно привести до спільного знаменника.
-
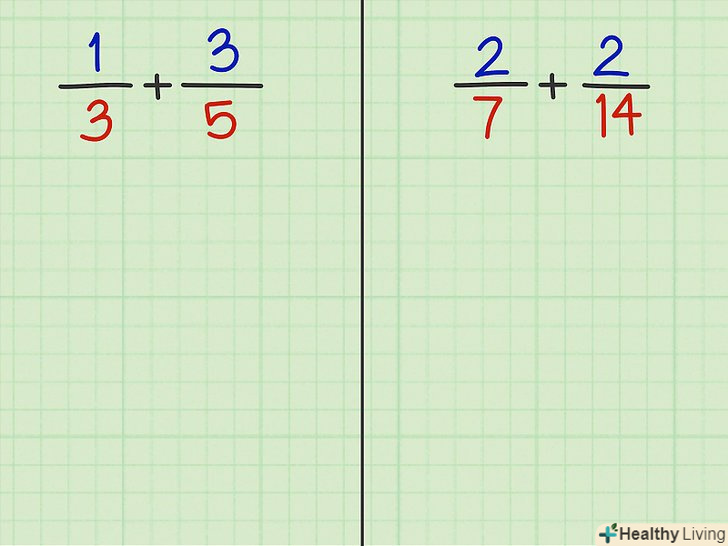
Розглянемо два приклади, на основі яких продемонструємо, як складати дроби з різними знаменниками.
- Приклад 3: 1/3 + 3/5
- Приклад 4: 2/7 + 2/14
-
Обчисліть загальний знаменник.для цього знайдіть загальний кратний знаменник. Найпростіший спосіб знайти загальне кратне-це просто перемножити знаменники. Якщо якийсь знаменник вже є загальним кратним, працювати потрібно тільки з рештою дробами.
- Приклад 3: 3 x 5 = 15. Таким чином, загальним знаменником даних дробів буде 15.
- Приклад 4: 14 кратно 7, тому просто помножте 7 на 2, щоб отримати 14. Таким чином, загальним знаменником даних дробів буде 14.
-
Помножте чисельник і знаменник першого дробу на знаменник другого дробу.зверніть увагу, що в цьому випадку значення вихідної дробу не зміниться.
- Приклад 3: 1/3 x 5/5 = 5/15.
- Приклад 4: чисельник і знаменник першого дробу помножте на 2, щоб привести перший дріб до спільного знаменника 14.
- 2/7 x 2/2 = 4/14.
-
Помножте чисельник і знаменник другого дробу на знаменник першого дробу.зверніть увагу, що в цьому випадку значення вихідної дробу не зміниться.
- Приклад 3: 3/5 x 3/3 = 9/15.
- Приклад 4: чисельник і знаменник другого дробу ні на що множити не потрібно, тому що знаменник цього дробу вже дорівнює спільному знаменнику.
-
Запишіть отримані дроби. Ми ще не склали їх, а просто помножили кожен дріб на 1, щоб привести їх до спільного знаменника.
- Приклад 3: 1/3 + 3/5 = 5/15 + 9/15
- Приклад 4: 2/7 + 2/14 = 4/14 + 2/14
-
Складіть чисельники дробів.чисельник-це число над рисою.
- Приклад 3: 5 + 9 = 14. 14-це чисельник кінцевого дробу.
- Приклад 4: 4 + 2 = 6. 6-це чисельник кінцевої дробу.
-
Запишіть спільний знаменник у знаменнику кінцевої дробу. тобто спільний знаменник і буде знаменником кінцевої дробу.
- Приклад 3: 15-це знаменник кінцевої дробу.
- Приклад 4: 14-це знаменник кінцевої дробу.
-
Запишіть кінцеву дріб на основі обчисленого чисельника і загального знаменника.
- Приклад 3: 1/3 + 3/5 = 14/15
- Приклад 4: 2/7 + 2/14 = 6/14
-
Спростіть і скоротіть кінцеву дріб. щоб скоротити дріб, розділіть чисельник і знаменник дробу на найбільший спільний дільник.
- Приклад 3: 14/15-цей дріб спростити/скоротити не можна.
- Приклад 4: 6/14 можна скоротити до 3/7. Для цього розділіть чисельник і знаменник дробу на 2 — це число є найбільшим загальним дільником.
Поради
- Перед тим як скласти чисельники дробів, переконайтеся, що їх знаменники однакові.
- Не складайте знаменники. Знайдіть спільний знаменник і не змінюйте його.
- Якщо потрібно скласти правильну або неправильну дріб зі змішаним числом, спочатку Перетворіть змішане число в неправильну дріб, а потім використовуйте дії, описані в цій статті.
