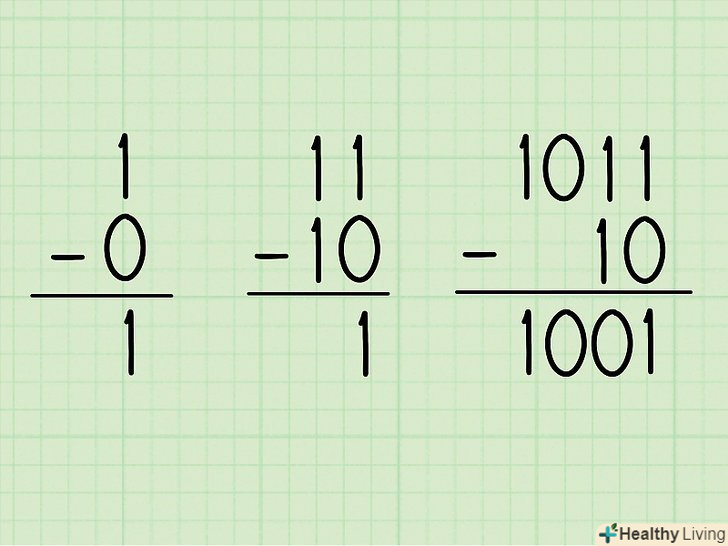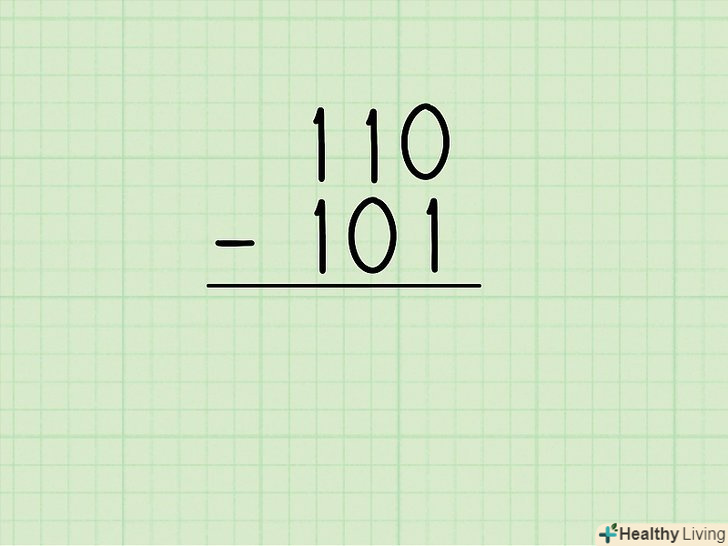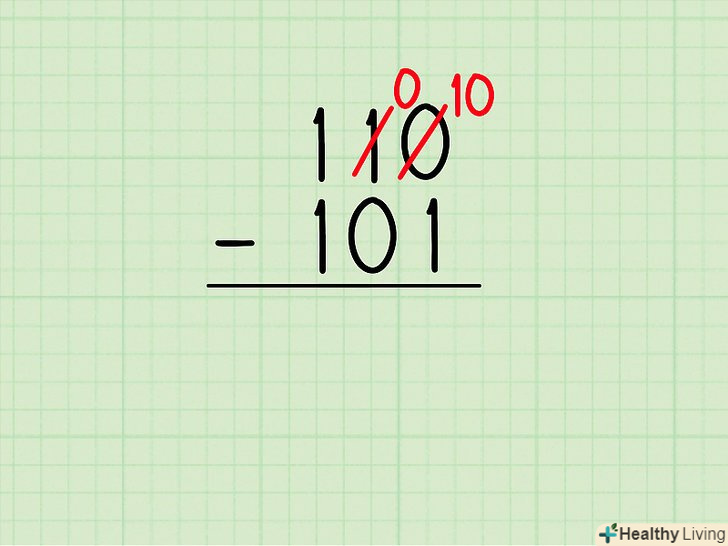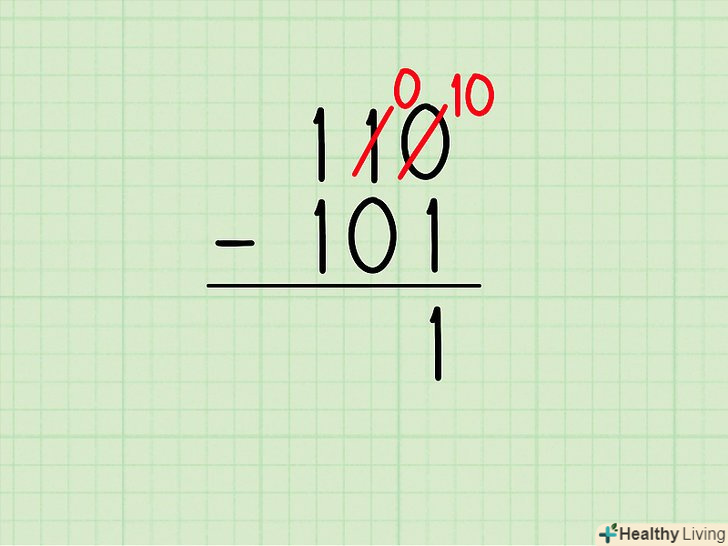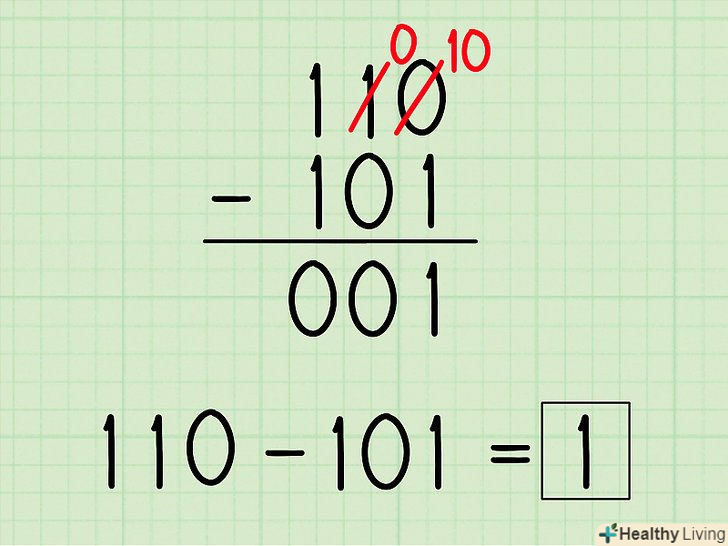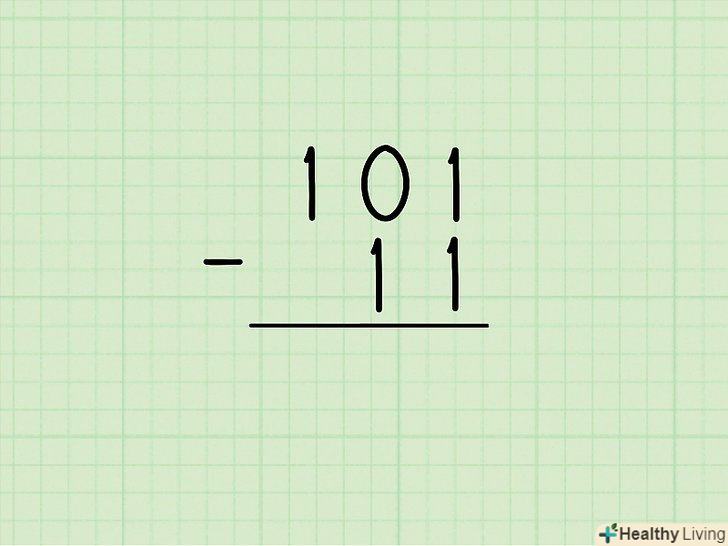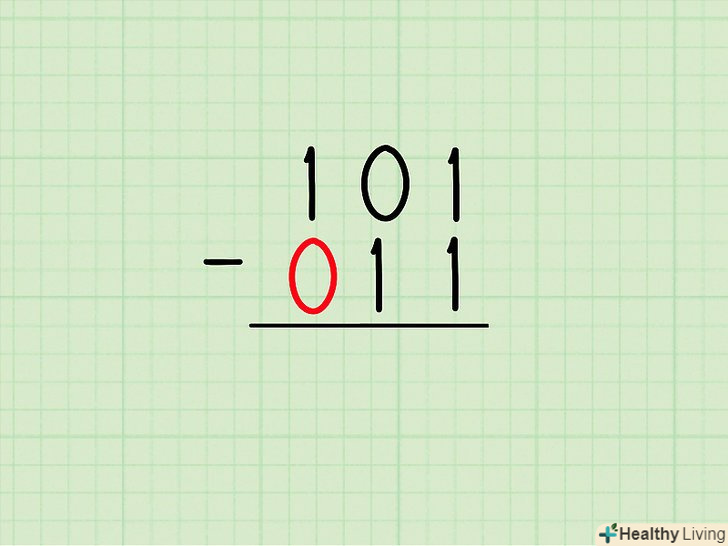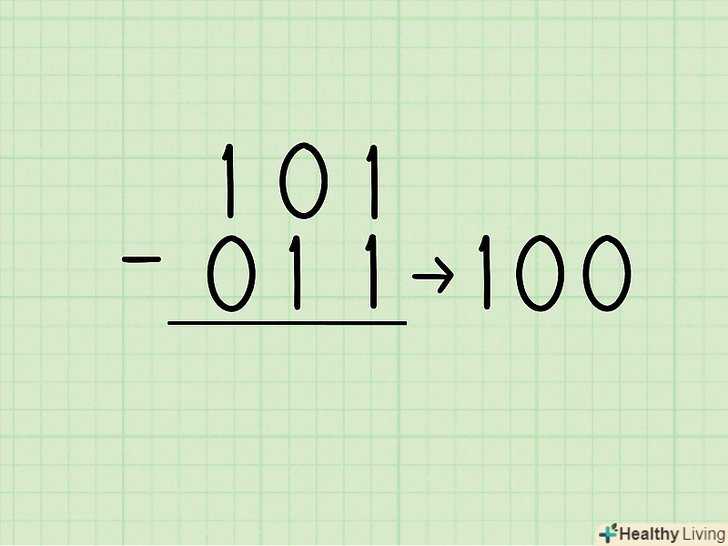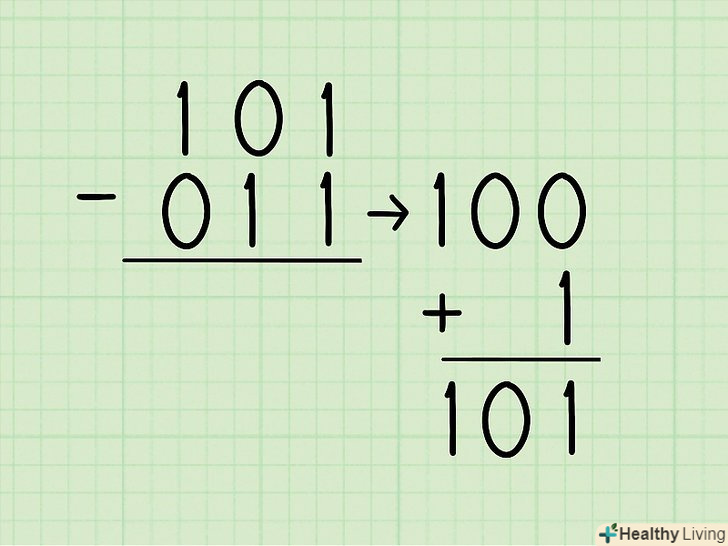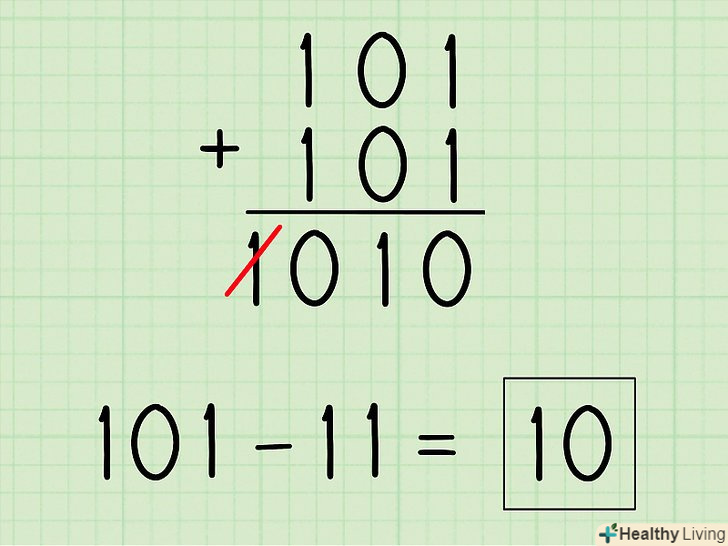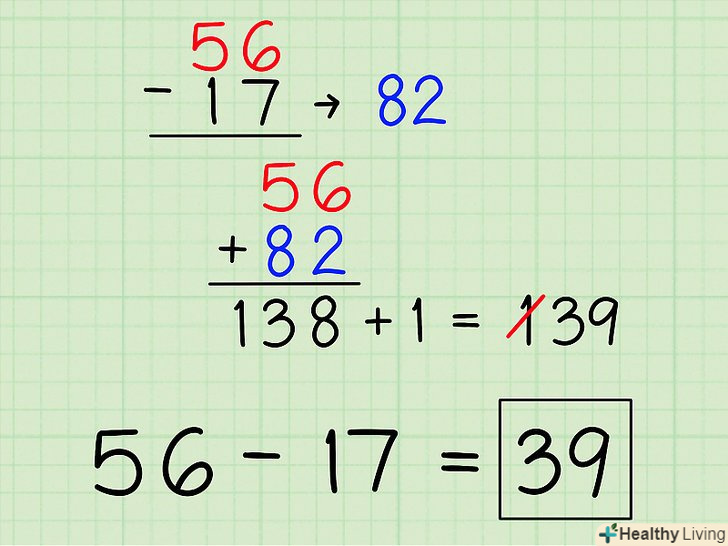1. Головна
    2. Математика
    3. Як віднімати двійкові числа: 15 кроків

Як віднімати двійкові числа: 15 кроків

Віднімання двійкових чисел трохи відрізняється від віднімання десяткових чисел.

Метод1 З 2:
Заимствование

  1. Запишіть двійкові числа один під одним-менше число під великим. Якщо менше число має менше цифр, вирівняйте його по правому краю (так, як ви записуєте десяткові числа при їх відніманні).
  2. Деякі завдання на віднімання двійкових чисел нічим не відрізняються від віднімання десяткових чисел.запишіть числа один під одним і, починаючи праворуч, знайдіть результат віднімання кожної пари чисел. Ось кілька простих прикладів:
    • 1 - 0 = 1
    • 11 - 10 = 1
    • 1011 - 10 = 1001
  3. Розглянемо більш складну задачу. необхідно запам'ятати тільки одне правило, щоб вирішувати завдання на віднімання двійкових чисел. Це правило описує запозичення цифри зліва, щоб ви могли відняти 1 з 0 (0 - 1). Вирішимо два завдання за допомогою методу запозичення.
    • 110 - 101 = ?
  4. У першому стовпці праворуч Ви отримуєте різницю 0-1.для її обчислення необхідно запозичити цифру зліва (з розряду десятків).
    • По-перше, закресліть 1 і замініть її на 0, щоб отримати таке завдання: 1010 - 101 = ?
    • Ви відняли ("запозичили") 10 з першого числа, тому ви можете написати це число замість цифри, що стоїть праворуч (в розряд одиниць).101100 - 101 = ?
  5. Відніміть цифри в правому стовпці. у нашому прикладі:
    • 101100 - 101 = ?
    • Правий стовпець:10 - 1 = 1. Якщо ви не зрозуміли, як отримати таку відповідь, прочитайте цю статтю:
    • 102 = (1 x 2) + (0 x 1) = 210 (цифри нижнього регістру позначають систему числення, в якій записані числа).
    • 12 = (1x1) = 110.
    • Таким чином, в десятковій системі ця різниця записується у вигляді: 2 - 1 = 1.
  6. Відніміть цифри в інших стовпцях.тепер це легко зробити (працюйте зі стовпцями, рухаючись справа наліво):
    • 101100 - 101 = __1 = _01 = 001 = 1.
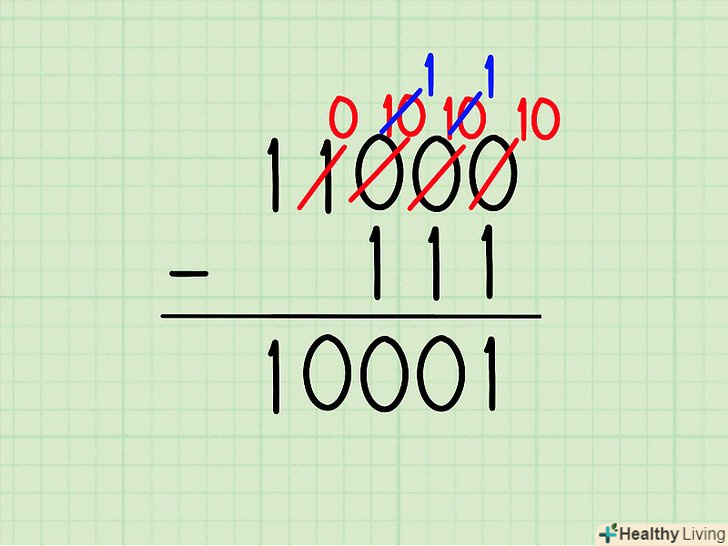
  7. Вирішіть складне завдання.у таких завданнях доведеться "запозичувати" цифри кілька разів тільки для того, щоб відняти цифри в одному стовпці. Наприклад, вирішити наступну задачу: 11000 - 111. Не можна «запозичувати» цифри у 0, тому пересувайтеся до наступної цифри зліва (до тих пір, поки ви не досягнете 1).
    • 10110000 - 111 =
    • 10111001000 - 111 = (запам'ятайте: 10 - 1 = 1)
    • 10111001100100 - 111 =
    • Ось як це записується в більш зрозумілому вигляді:1011100 - 111 =
    • Обчисліть різницю цифр у всіх стовпцях (рухаючись справа наліво):_ _ _ _ 1 = _ _ _ 0 1 = _ _ 0 0 1 = _ 0 0 0 1 = 1 0 0 0 1
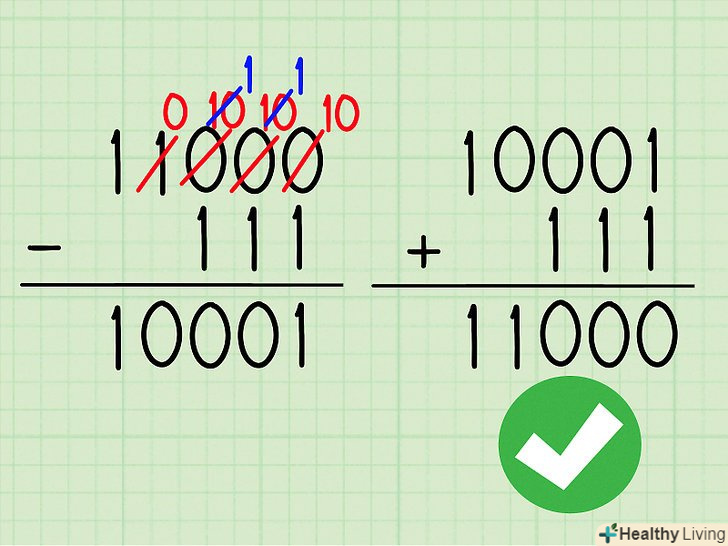
  8. Перевірте відповідь.є три способи зробити це.[1] швидкий спосіб-відкрийте двійковий онлайн калькулятор і введіть в нього умови завдання. Два інших методу мають на увазі перевірку відповіді вручну (вони можуть стати в нагоді вам на іспиті).
    • складіть двійкові числа, щоб перевірити відповідь. Складіть відповідь з меншим числом; ви повинні отримати більше число. В останньому прикладі (11000 - 111 = 10001): 10001 + 111 = 11000, тобто відповідь правильна.
    • Крім того, ви можетеперетворити двійкові числа в десяткові і перевірити відповідь. В останньому прикладі (11000 - 111 = 10001) при перетворенні Ви отримаєте: 24-7 = 17, тобто відповідь правильна.

Метод2 З 2:
Доповнення

  1. Запишіть двійкові числа один під одним так, як ви записуєте десяткові числа при їх відніманні.цей метод використовується комп'ютерами для віднімання двійкових чисел, так як він заснований на більш ефективному алгоритмі. Однак простій людині, яка звикла віднімати десяткові числа, цей метод може здатися більш складним (якщо ви програміст, обов'язково ознайомтеся з цим методом віднімання двійкових чисел).[2]
    • Розглянемо приклад: 101-11=?
  2. Якщо значність чисел різна, до числа з меншою значністю зліва припишіть відповідну кількість 0.наприклад, якщо дані числа 101 (тризначне) і 11 (двозначне), Перетворіть двозначне число в тризначне, приписавши йому зліва один 0: 011.
    • 101 - 011 = ?
  3. У віднімається числі поміняйте цифри: кожну 1 поміняйте на 0, а кожен 0 на 1. У нашому прикладі віднімається перетворюється в: 011 → 100.
    • Насправді ми "забираємо доповнення у одиниці", тобто віднімаємо кожну цифру з 1. Це працює в двійковій системі, так як у такої «заміни» може бути тільки два можливих результату: 1 -0 = 1 і 1 - 1 = 0.
  4. ДоОтриманого віднімається додайте 1.у нашому прикладі ви отримаєте 100 + 1 = 101.
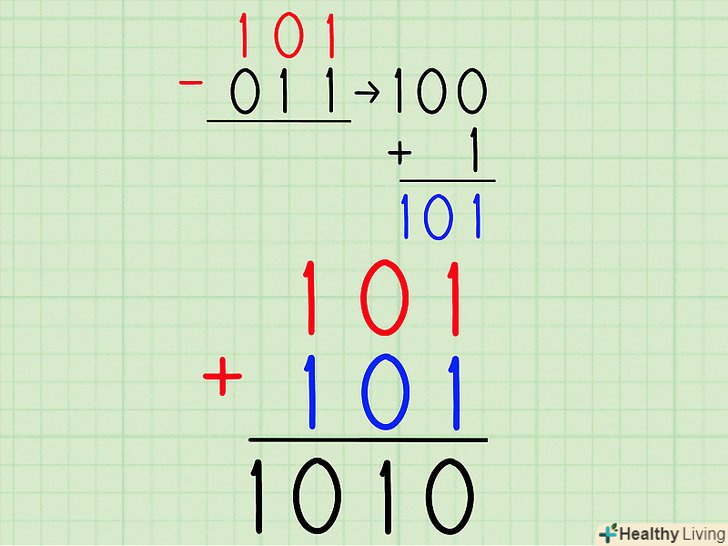
  5. Тепер замість віднімання складіть два двійкових числа.
    • 101 + 101 = 1010
    • Якщо ви не знаєте, як складати двійкові числа, прочитайтецю статтю.
  6. В отриманому результаті ігноруйте будь-яку цифру, що стоїть першою зліва (так як ви отримали число не тієї значності).у нашому прикладі ви складали тризначні числа (101 + 101), а отримали чотиризначну відповідь (1010). Тому закресліть першу цифру зліва, і ви отримаєте остаточну відповідь Вашого завдання.[3]
    • 1010 = 10
    • Таким чином,101 - 011 = 10
    • Якщо зайвої цифри немає, то ви віднімали більше число з меншого. Дивіться розділ "поради" про те, як вирішувати такі завдання.
  7. Спробуйте застосувати цей метод до десяткових чисел.цей метод називається "Доповнення до двійці«, так як заміна цифр призводить до» Доповнення до одиниці", а потім до отриманого числа додається 1.[4] для кращого з'ясування цього методу розглянемо наступний приклад:
    • 56 - 17
    • Так як в прикладі розглядаються десяткові числа, то кожну цифру віднімається (17) відніміть з 9: 99 - 17 = 82.
    • Складіть два числа: 56 + 82. Якщо ви порівняйте це підсумовування з вихідною задачею (56-17), то ви побачите, що до вихідної задачі додали 99.
    • 56 + 82 = 138. Так як до вихідної задачі додали 99, потрібно відняти 99 з відповіді. Необхідно діяти аналогічно обчислень з двійковими числами: додайте до результату 1, а потім ігноруйте першу цифру зліва.
    • 138 + 1 = 139 →139 → 39. Це рішення вихідної задачі (56 - 17 = 39).

Поради

  • Для віднімання більшого числа з меншого, відніміть менше число з більшого, а до відповіді припишіть знак «мінус». Наприклад, щоб обчислити 11 - 100, обчисліть 100 - 11, а потім до відповіді припишіть знак «мінус» (це правило відноситься до віднімання чисел в будь-якій системі числення, а не тільки в двійковій системі).
  • Метод Доповнення працює наступним чином: a - b = a + (2n - b) - 2n. якщо n дорівнює розрядності b, то 2n - b на одиницю більше результату віднімання кожного розряду.

Джерела

  1. ↑ Http://www.exploringbinary.com/binary-subtraction/
  2. ↑ Http://www.exploringbinary.com/binary-subtraction/
  3. ↑ Http://courses.cs.vt.edu/csonline/NumberSystems/Lessons/SubtractionWithTwosComplement/index.html
  4. ↑ Http://courses.cs.vt.edu/csonline/NumberSystems/Lessons/SubtractionWithTwosComplement/index.html

Ще почитати: