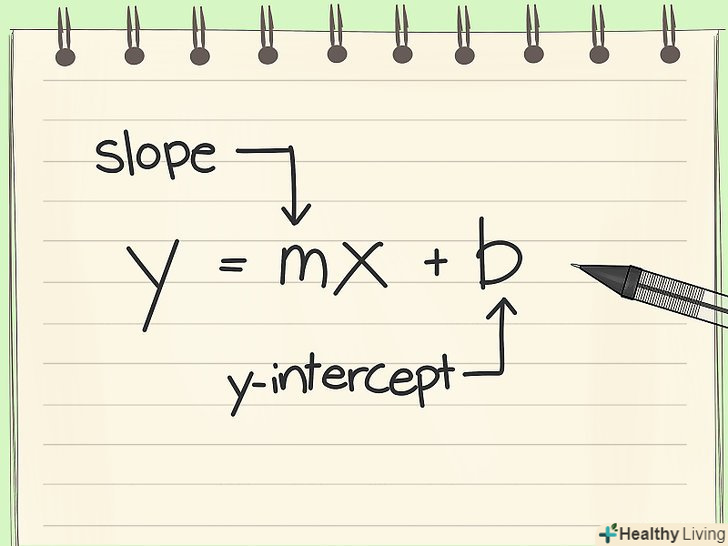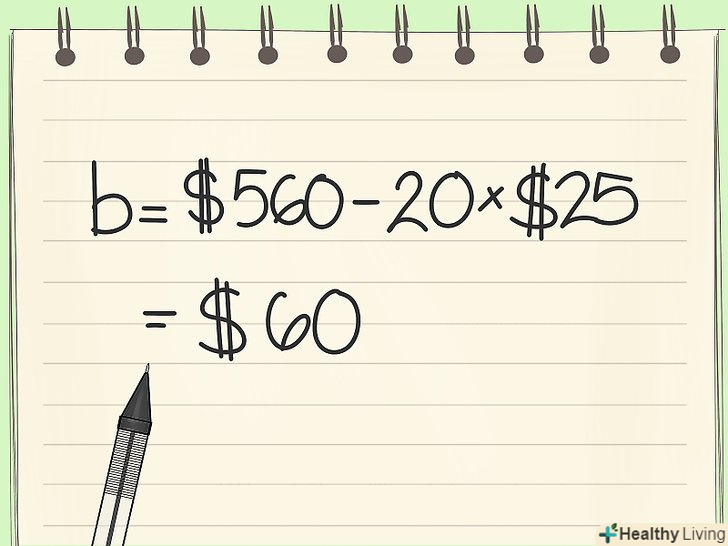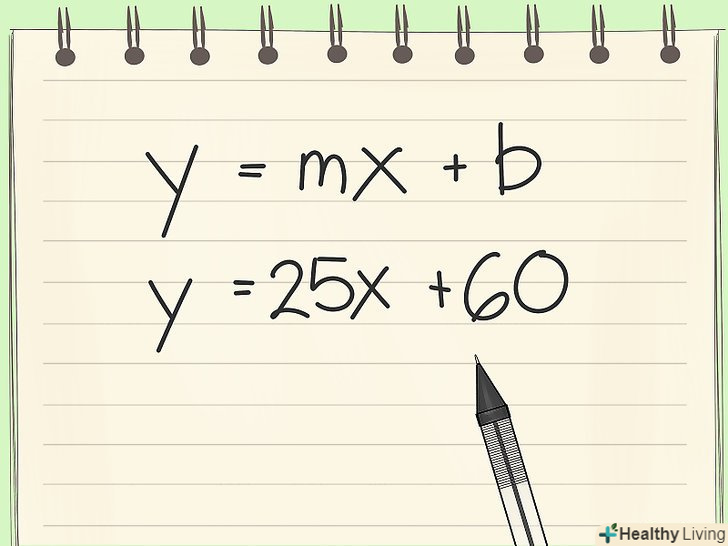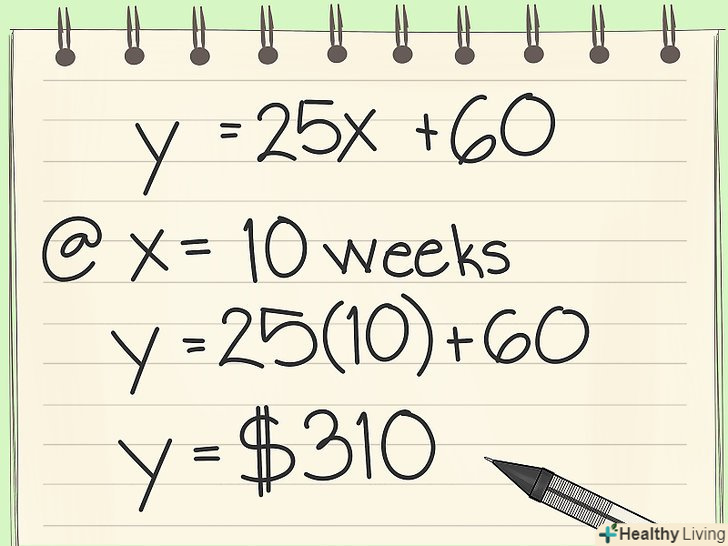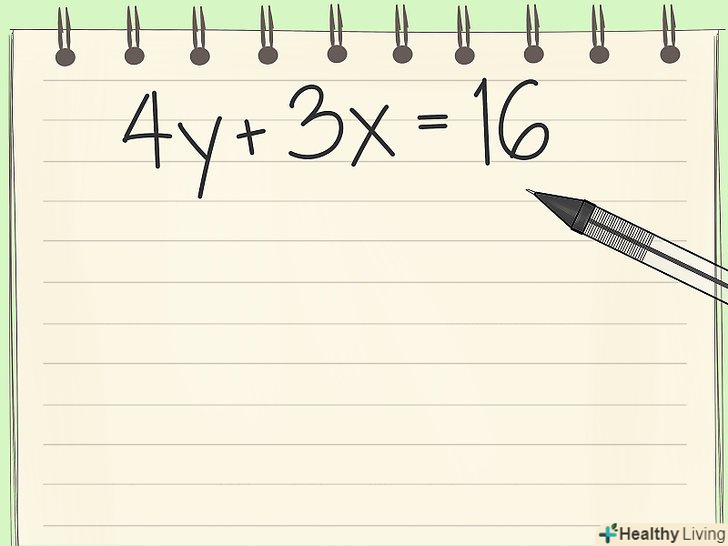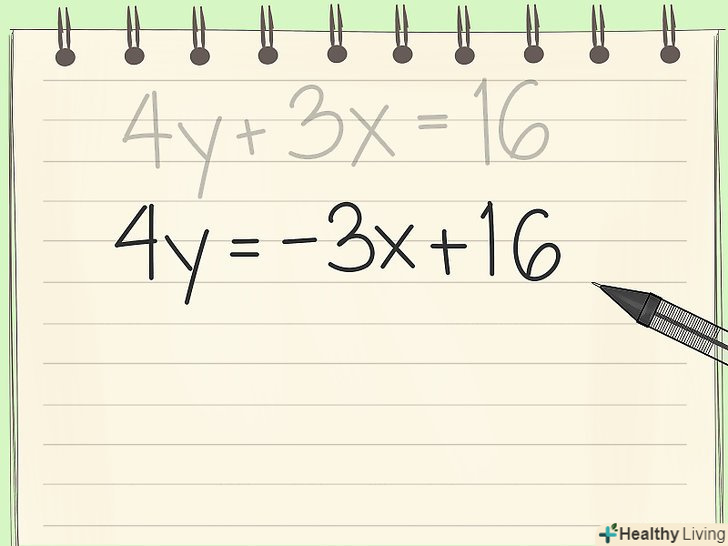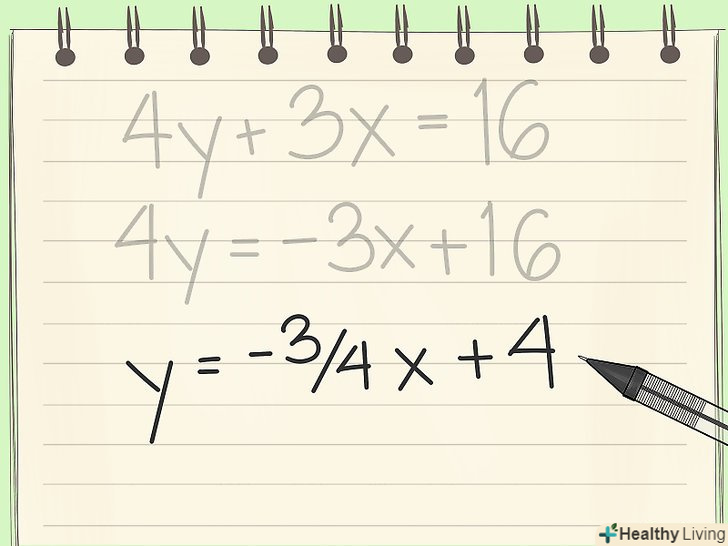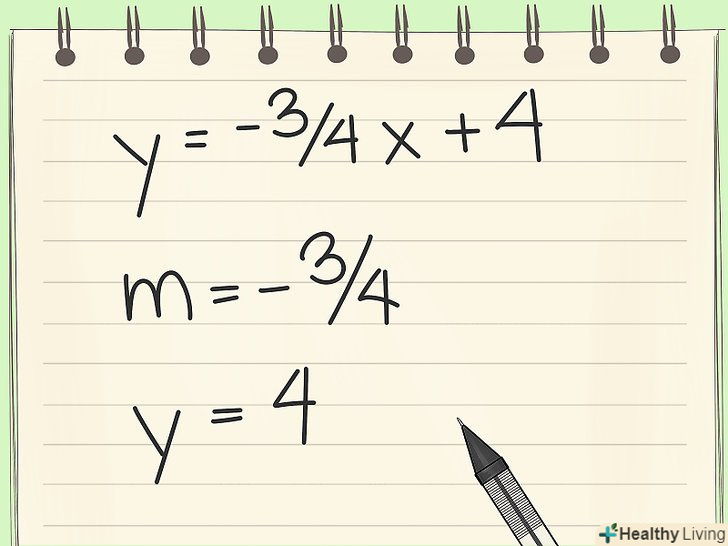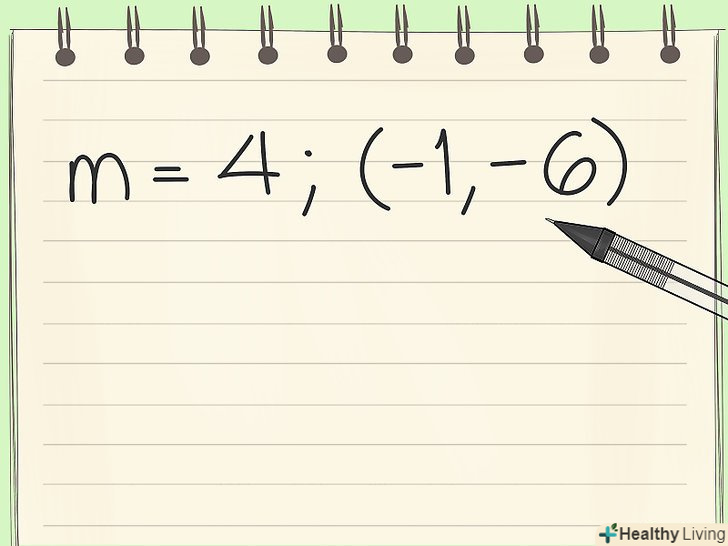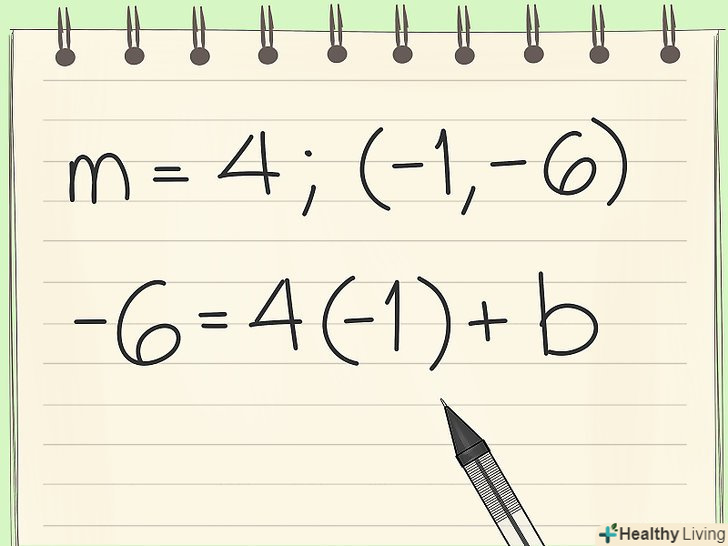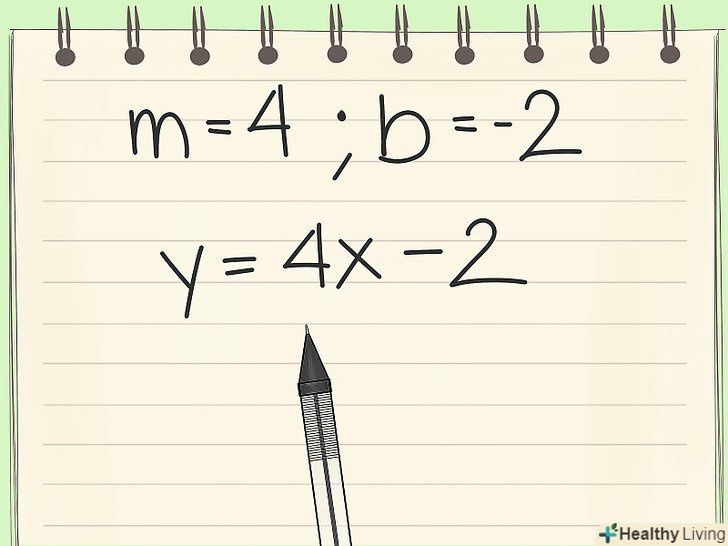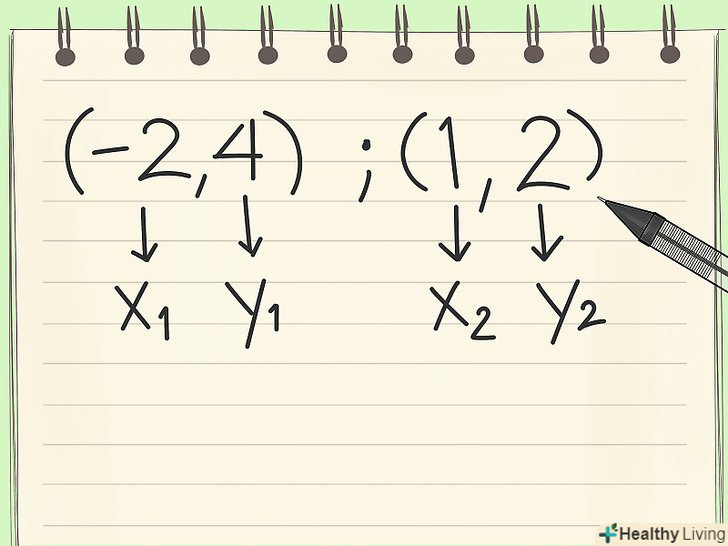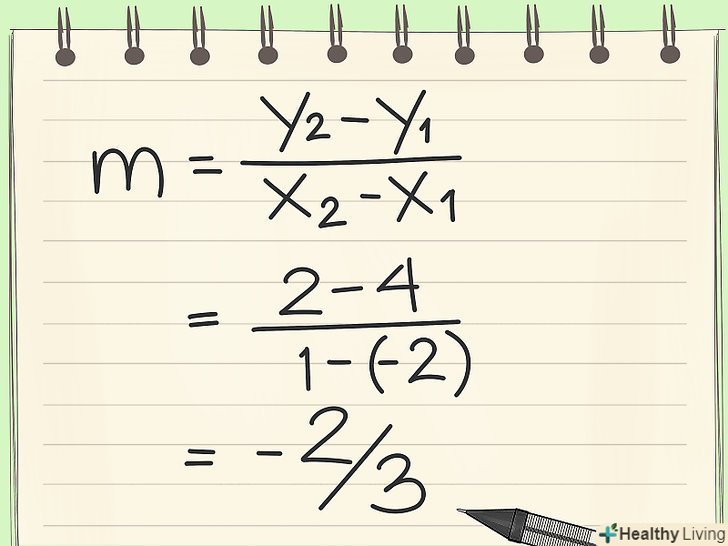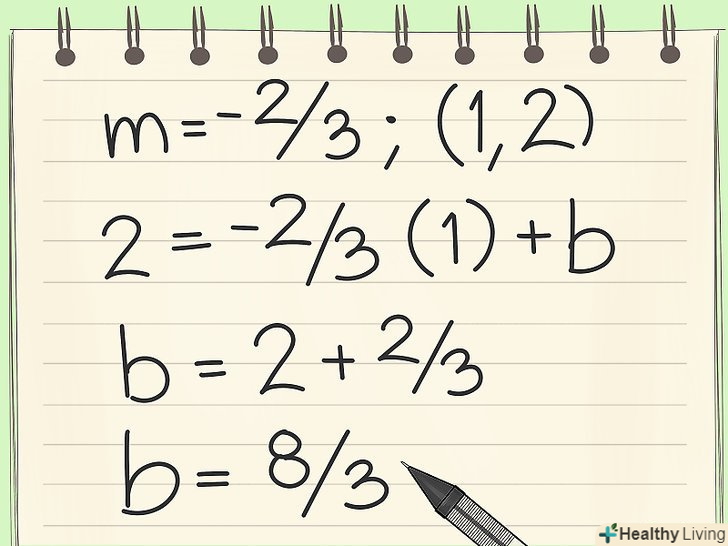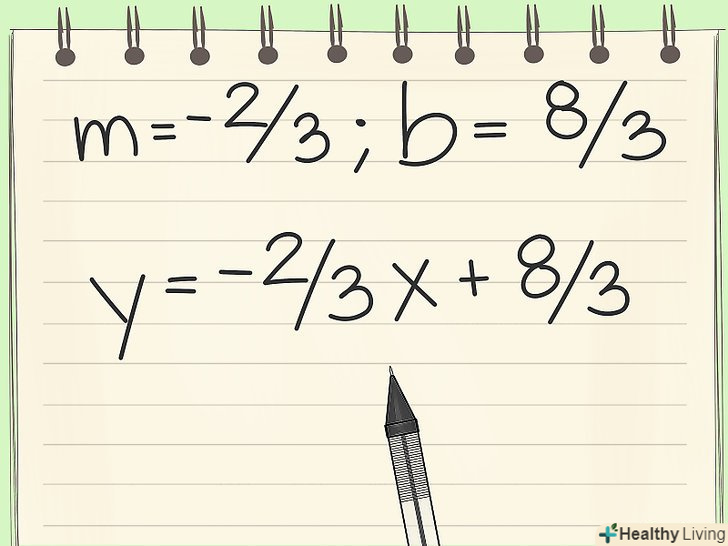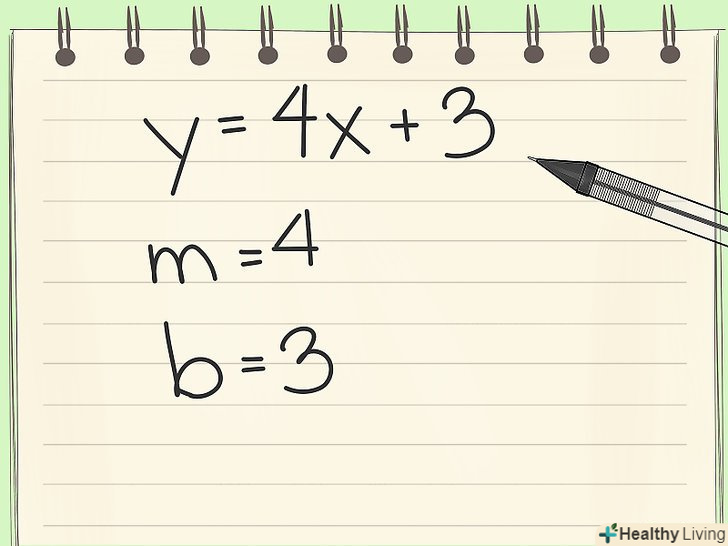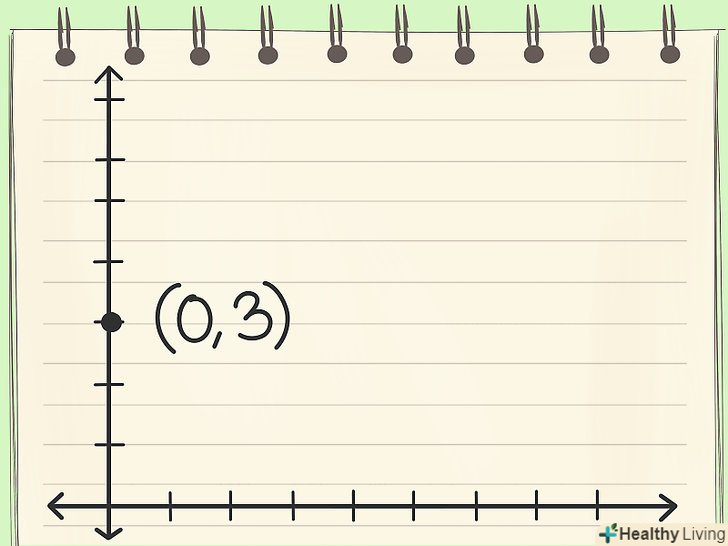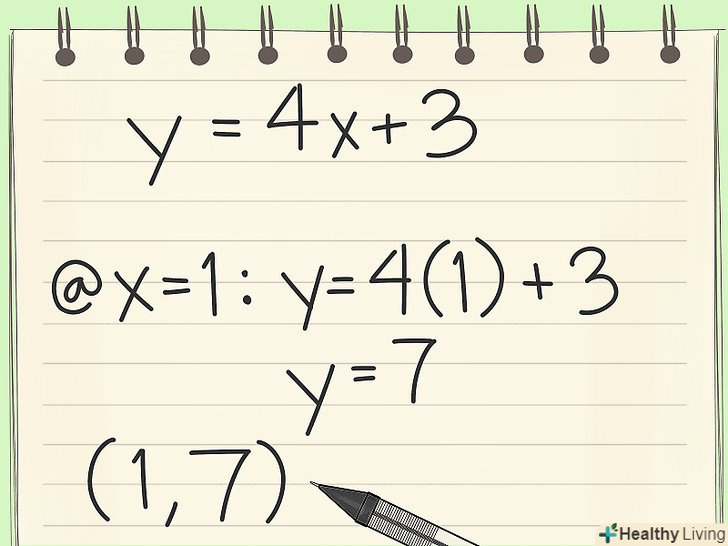1. Головна
    2. Математика
    3. Як застосовувати лінійну функцію ( з алгебри)

Як застосовувати лінійну функцію ( з алгебри)

Лінійна функція записується у вигляді "y = mx + b", дезначення букв повинні бути підставлені або знайдені, тобто:" x "і" y " - координати прямої,," m " – кутовий коефіцієнт (кут нахилу прямої до осі х)," b " – вільний член (точка перетину прямої з віссю y). Якщо ви хочете навчитися застосовувати лінійну функцію, прочитайте цю статтю.

Метод1З 5:
Лінійна функція для вирішення нематематичних задач

  1. Зрозумійте завдання.перед тим, як приступити до вирішення, Ви повинні уважно прочитати завдання для з'ясування поставленого питання. Наприклад: сума на вашому банківському рахунку зростає лінійно. Якщо після 20 тижнів на вашому рахунку лежить $560, а після 21 тижня - $585, висловіть в лінійній формі залежність накопиченої суми від кількості минулих тижнів.
  2. Подумайте, як представити рішення у вигляді лінійної функції. запишіть Y = mx + b і врахуйте, що "m" – кут нахилу, а "b" – точка перетину. Зауважте, що "сума на вашому банківському рахунку зростає лінійно", тобто значення накопичуваної суми за певний період часу постійно і тому Графік в цьому випадку - пряма. Якщо сума, що накопичується різна в певній період часу, то графік не може бути прямою.
  3. Знайдіть кутовий коефіцієнт (нахил) прямий.для цього обчисліть зміну значення функції (в даному випадку - сума на рахунку). Якщо через 20 тижнів сума дорівнює $560, а ще через тиждень - $585, то ви заробили $25 ($585 - $560 = $25) за 1 тиждень.
  4. Знайдіть точку перетину з віссю у. щоб знайти точку перетину з віссю у, або "B" В y = mx + b, необхідно знати стартову суму на рахунку. Якщо у вас $560 після 20 тижнів і ви знаєте, що заробляєте $ 25 за кожен тиждень, то помножте 20 х 25 і з'ясуйте, скільки грошей ви заробили за 20 тижнів. 20 х 25 = 500, тобто ви заробили $500 за 20 тижнів.
    • Так як на рахунку $560 після 20 тижнів і за цей термін ви заробили $500, то початкова сума на рахунку: $560 - $500 = $60.
    • Таким чином " b " (або або точка перетину з віссю у) = 60.
  5. Записуємо рівняння у вигляді лінійної функції.тепер, коли вам відомо, що m= 25 (приріст $25 за 1 тиждень), а b=60, Ви можете підставити їх у рівняння:
    • Y = mx + b
    • Y = 25x + 60
  6. Перевірте рівняння.у цьому рівнянні" у "- кількість зароблених (накопичених) грошей, а " х " - кількість тижнів. Спробуйте підставити в рівняння різну кількість тижнів, щоб обчислити накопичену суму. Спробуйте два приклади:
    • Скільки грошей ви заробите протягом 10 тижнів? Для цього підставте " 10 "замість" х " в рівняння.
      • Y = 25x + 60 =
      • Y = 25(10) + 60 =
      • Y = 250 + 60 =
      • Y = 310. За 10 тижнів ви заробите $310.
    • Скільки тижнів вам потрібно працювати, щоб накопичити $800? Підставте " 800 "замість" у "і знайдіть"х".
      • Y = 25x + 60 =
      • 800 = 25x + 60 =
      • 800 - 60 =
      • 25x = 740 =
      • 25x/25 = 740/25 =
      • X = 29.6. Ви можете заробити $800 протягом приблизно 30 тижнів.

Метод2З 5:
Перетворення рівняння в лінійну функцію

  1. Запишіть рівняння. припустимо, вам дано рівняння4y +3x = 16.
  2. Виділіть змінну у. перенесіть змінну х на одну сторону рівняння. Пам'ятайте про зміни знака при перенесенні за знак рівності. Тобто "3x", переміщена в іншу частину рівняння, стане "- 3х". Рівняння має виглядати як:
    • 4y + 3x = 16 =
      • 4y + 3x - 3x = -3x +16
    • 4y = -3x +16
  3. Розділіть всі члени рівняння на коефіцієнт при У. якщо при у коефіцієнта немає, то нічого робити не потрібно. Якщо є коефіцієнт, то потрібно розділити кожен член рівняння на це число. У нашому випадку коефіцієнт при у - це 4, так що ділимо 4у, - 3x, і 16 на 4, щоб отримати остаточну відповідь у вигляді лінійної функції.
    • 4y = -3x +16=
    • 4/4y = -3/4x +16/4
    • Y =-3/4x + 4
  4. Визначте члени рівняння. якщо ви використовуєте рівняння для побудови графіка, то" у "являє собою координати у," -3/4 " – кутовий коефіцієнт," х " - координати х," 4 " – координата перетину з з віссю у.

Метод3З 5:
Знаходження лінійної функції, коли відомі кутовий коефіцієнт і точка на прямій

  1. Запишіть рівняння у вигляді лінійної функції.по-перше, просто напишіть Y = mx + b. Припустимо, дана наступна задача: знайти рівняння прямої, у якій кутовий коефіцієнт = 4 і вона проходить через точку (-1,-6)
  2. Підставте значення. " m " – кутовий коефіцієнт = 4," у "І" х " - координати даної точки. В цьому випадку, " х "= -1 і" у " = -6. "b" - координата перетину з віссю у (вона нам невідома).
    • Y = -6, m = 4, x = -1 (дані значення)
    • Y = mx + b (рівняння)
    • -6 = (4)(-1) + b
  3. Знайдіть координату перетину з віссю у.
    • -6 = (4)(-1) + b
    • -6 = -4 + b
    • -6 +4 = b
    • -2 = b
  4. Напишіть рівняння . Тепер, коли Ви знайшли "b" , ви можете записати рівняння у вигляді лінійної функції:
    • M = 4, b = -2
    • Y = mx + b
    • Y = 4x -2

Метод4З 5:
Знаходження лінійної функції, коли відомі дві точки на прямій

  1. Запишіть дві точки. нехай дана задача: знайти рівняння прямої, яка проходить через точки (-2 , 4) і ( 1 , 2)
  2. Використовуйте дві точки для обчислення кутового коефіцієнта.Формула знаходження кутового коефіцієнта прямої, яка проходить через дві точки: (Y2 - Y1) / (X2 - X1). Тут X1 і Y1 - координати першої точки (-2,4), А X2 і Y2 - координати другої точки (1,2). Тепер підставте їх у формулу:
    • (Y2 - Y1) / (X2 - X1) =
    • (2 - 4)/(1 - -2) =
    • -2/3 = m
    • Кутовий коефіцієнт = -2 / 3.
  3. Виберіть одну з точок для обчислення координати перетину з віссю у. Не має значення, яку точку ви візьмете. Тепер просто підставте значення в рівняння y = mx + b, де " m " – кутовий коефіцієнт," x "і" y " - координати обраної точки. Знаходимо b:
    • Y = 2, x, = 1, m = -2/3
    • Y = mx + b
    • 2 = (-2/3)(1) + b
    • 2 = -2/3 + b
    • 2 + 2/3 = b, або b =8 / 3
  4. Підставте знайдені значення у вихідне рівняння.тепер, коли вам відомо, що кутовий коефіцієнт =-2/3 , а вільний член = 2 2/3, просто підставте їх у вихідне рівняння для прямої.
    • Y = mx + b
    • Y =-2/3x + 2 2/3

Метод5З 5:
Побудова графіка лінійної функції

  1. Запишіть рівняння. припустимо, дано рівнянняY = 4x + 3.
  2. Почніть графік з точки перетину з віссю у. вільний член в нашому прикладі = "+ 3", тобто позитивна величина. Це означає, що пряма перетинає вісь у в точці (0 ,3).
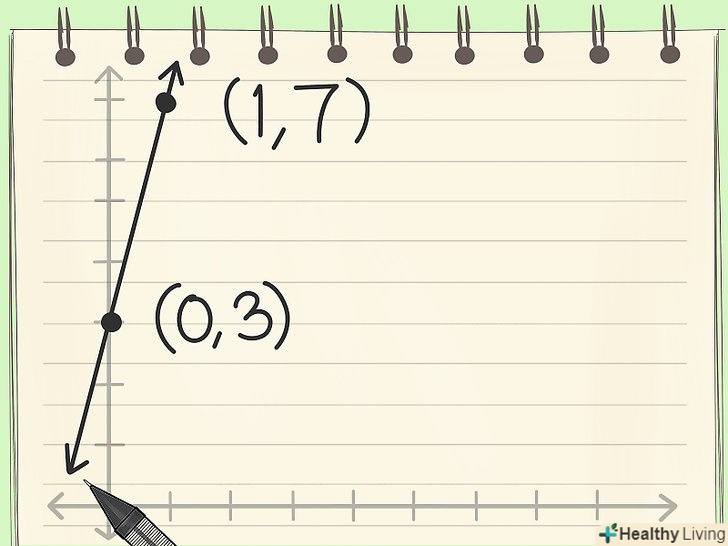
  3. Використовуйте кутовий коефіцієнт для обчислення координати іншої точки на прямій. кутовий коефіцієнт =4 і це означає, що при зростанні координати у на 4 одиниці, координата х збільшується на 1 одиницю. Відповідно, якщо ви починаєте в точці (0,3), то наступна точка на прямій - (1,7).
    • Якщо кутовий коефіцієнт-негативна величина, то наступна точка лежить нижче точки перетину прямої з віссю у.
  4. З'єднайте дві точки.тепер все, що вам потрібно зробити, це провести пряму лінію через ці дві точки, і ви отримаєте графік лінійної функції. Ви можете продовжувати обчислювати координати точок на прямій (взяти нову точку як початкову точку і знайти наступну).

Поради

  • Кутовий коефіцієнт прямої дорівнює тангенсу кута між позитивним напрямком осі абсцис і даної прямої.
  • Спробуйте перевірити свої відповіді. Якщо вам дані або Ви знайшли координати х і у, підставте їх назад в рівняння. Наприклад, якщо х = 10, а саме Ви знайшли х=10 в рівнянні y=x+3, підставте 10 замість х.відповіддю повинна бути відповідна координата у, у = 13 в точці (х, у) = (10, 13). Y=13 може бути графічно представлена у вигляді прямої горизонтальної лінії, що перетинає вісь у, з кутовим коефіцієнтом =0 вертикальна лінія матиме нескінченний (неіснуючий) кутовий коефіцієнт.
  • Алгебра-наука, заснована на обчисленнях. Ви повинні їх записувати для найкращого засвоєння процесу.
  • Якщо ви робите найпростіші обчислення в своєму розумі, не записуючи, то при вирішенні більш складного завдання це може привести до помилок.
  • При прискоренні або зменшенні швидкості руху (швидкість не лінійна), графік рівняння такого руху не буде прямою лінією. Однак середня швидкість руху за певний проміжок часу змінюється рівномірно, і графік в цьому випадку – пряма лінія. Тому в багатьох завданнях дана саме середня швидкість.
  • Використовуйте калькулятор. Ви зможете знайти рівняння прямої за допомогою лінійної регресії даних, яка робиться автоматично за допомогою програми калькулятора. Цим треба користуватися після того, як ви навчитеся робити все це вручну. Калькулятор-зручний інструмент в руках досвідченого математика.
  • Записуйте приклади і практикуйтеся у вирішенні завдань для засвоєння процесу обчислень.
  • Ви справите враження на викладача, якщо зрозумієте, як застосувати лінійне рівняння для будь-якої задачі.
  • Декартова система координат, що використовується для побудови графіків рівнянь і т.д., була названа на честь французького вченого Рене Декарта. Ця система використовується в математиці, астрономії, навігації, для освітлення пікселів на екранах комп'ютерів і взагалі скрізь, де потрібне визначення координат.
  • Не забудьте помножити перед складанням, коли працюєте з рівнянням y = mx + b. тобто не складайте х + b, а спочатку помножте m на x.

Ще почитати: