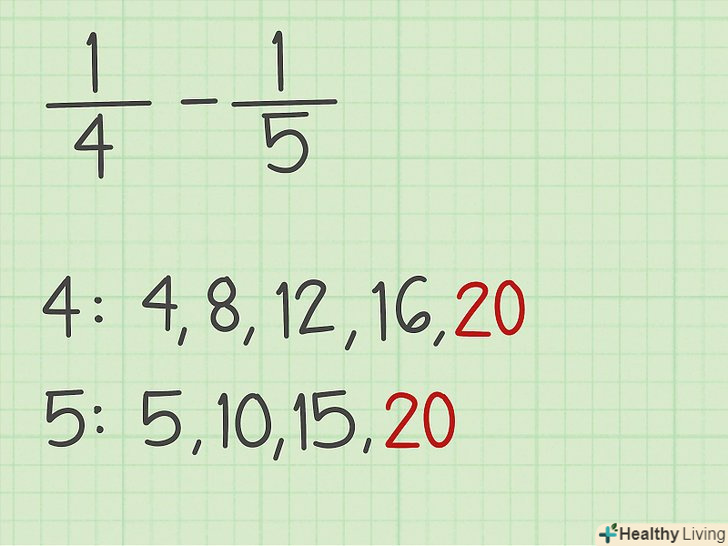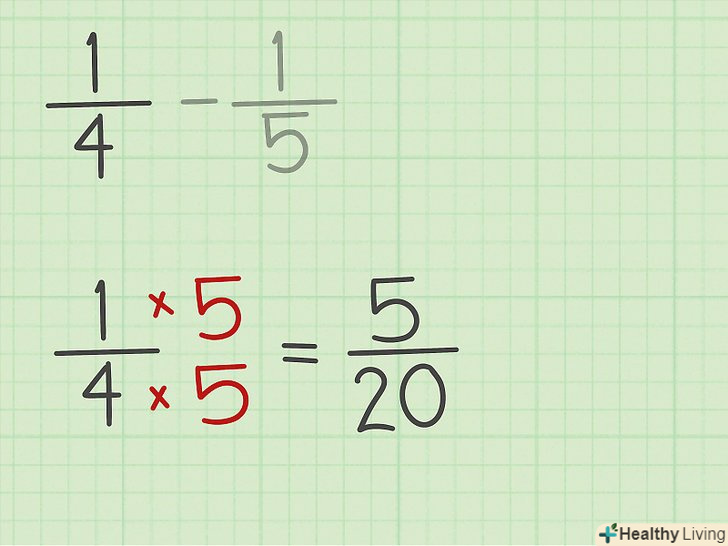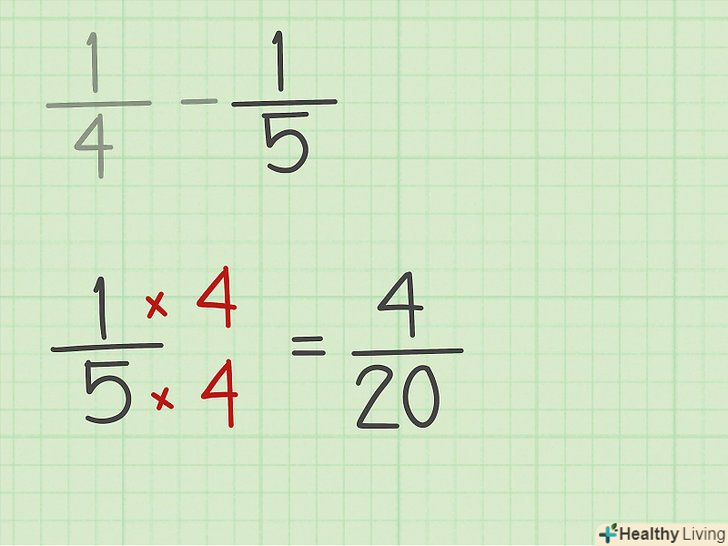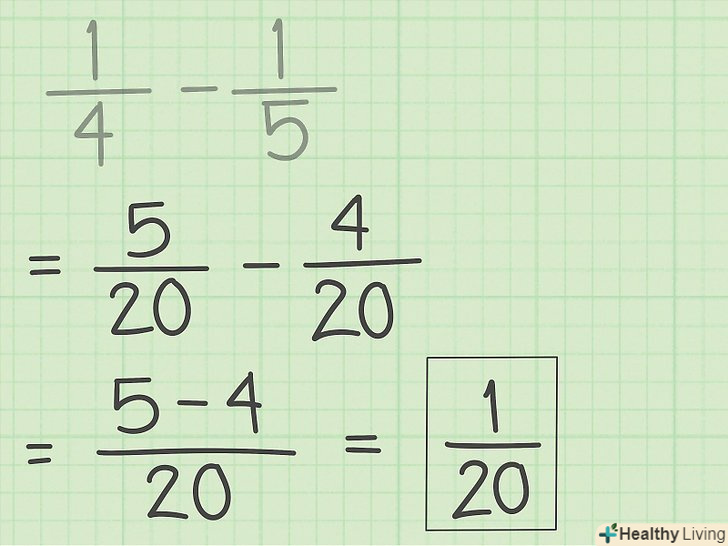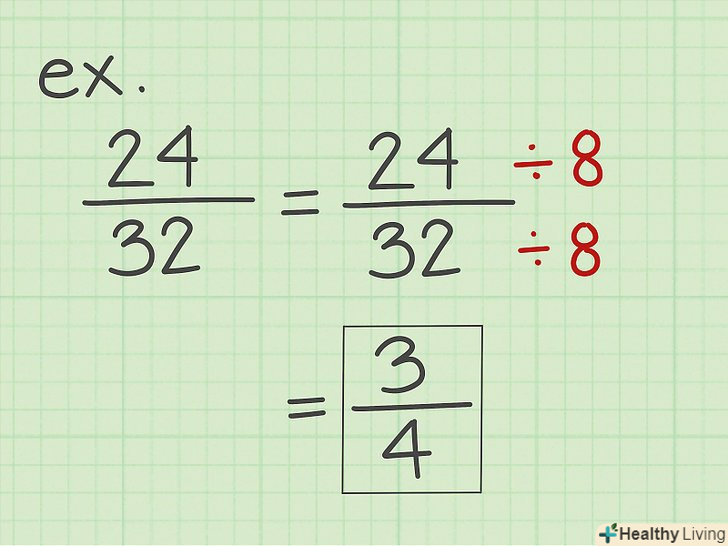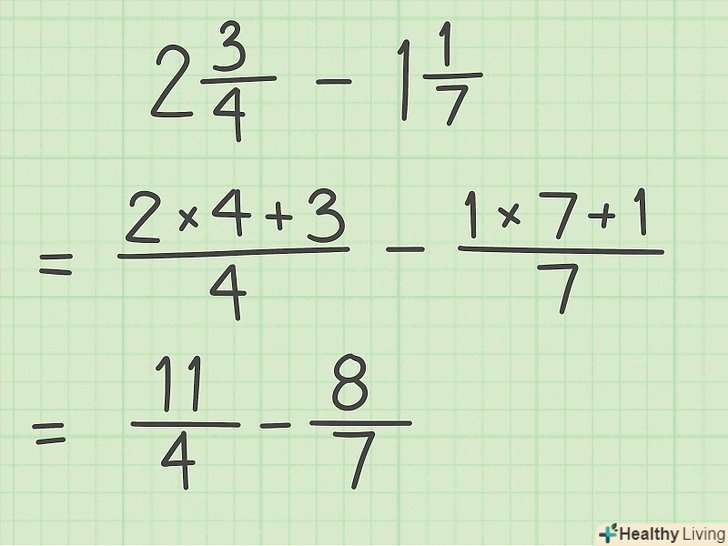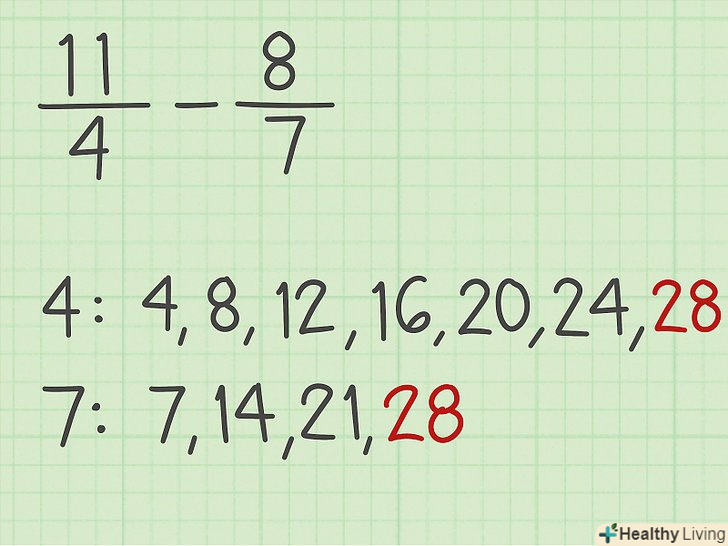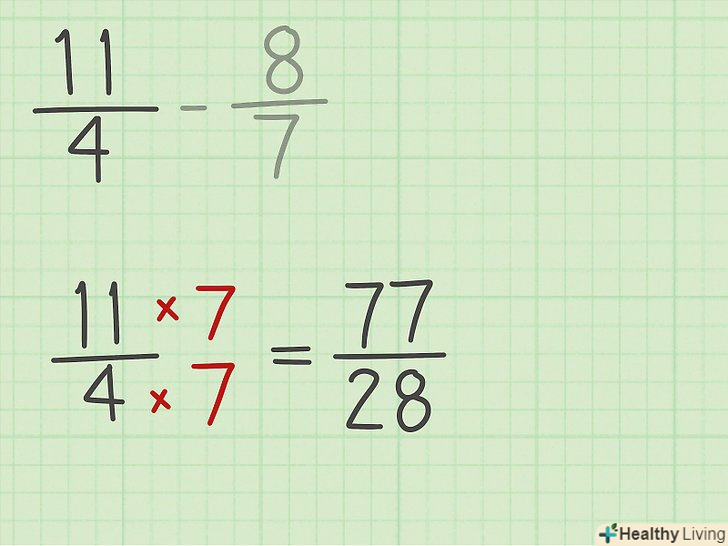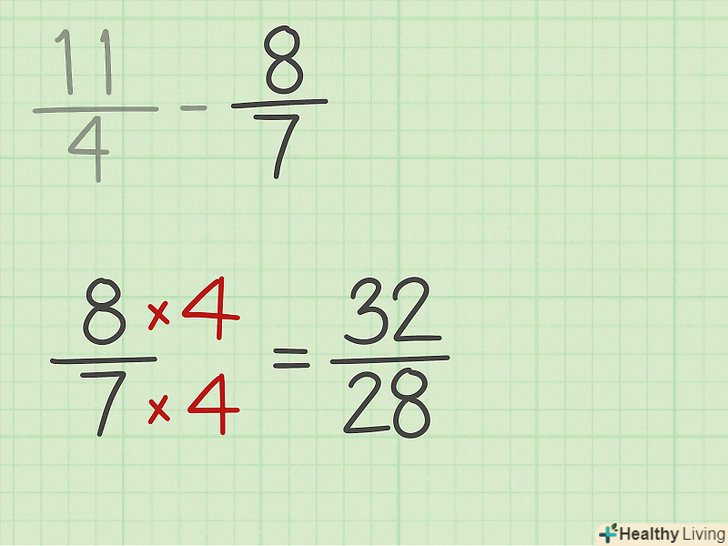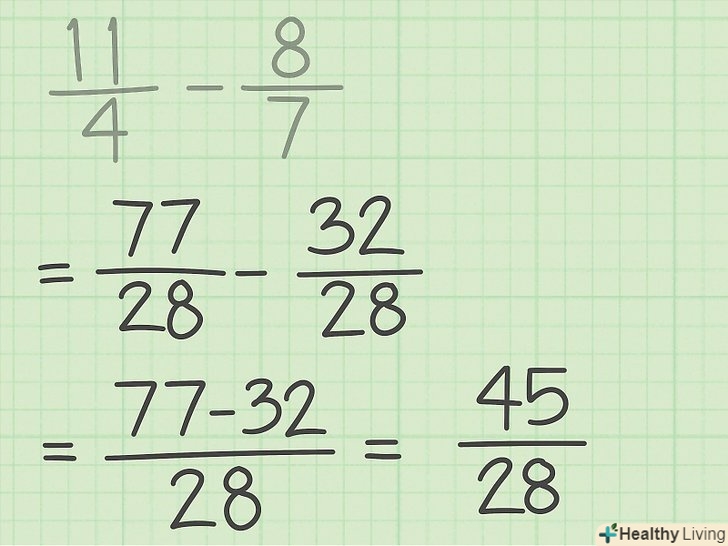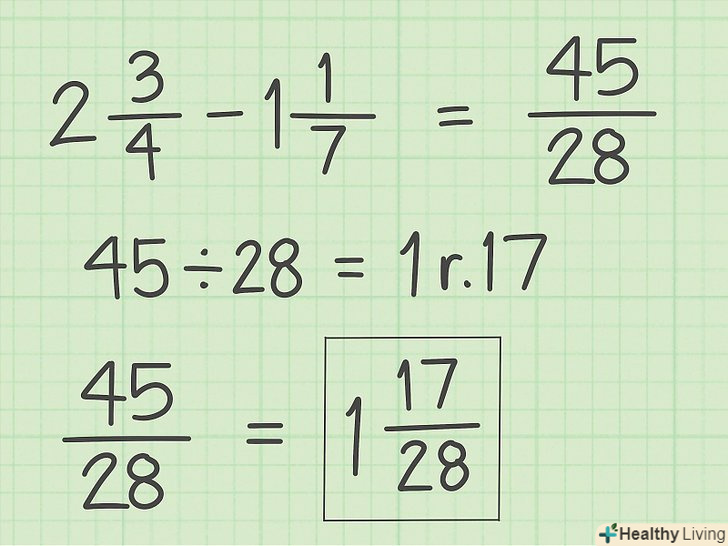На перший погляд віднімати дробу не так-то просто, але якщо застосувати найпростішу операцію множення, ви швидко віднімете одну дріб з іншої. Якщо дроби правильні, потрібно привести їх до спільного знаменника, а потім відняти чисельники. Якщо дані змішані числа, перетворіть їх в неправильні дроби, приведіть їх до спільного знаменника, а потім відніміть чисельники.
Кроки
Метод1 З 2:
Як знайти найменше спільне кратне (НОК) і відняти дроби
Метод1 З 2:
 Випишіть кратні знаменників (при необхідності).якщо знаменники дробів не рівні один одному, потрібно зробити їх рівними. Випишіть кратні кожного знаменника, щоб знайти число, яке є кратним обох знаменників. Наприклад, дано вираз 1/4-1/5; випишіть всі кратні 4 і 5, щоб знайти, що НОК = 20.[1]
Випишіть кратні знаменників (при необхідності).якщо знаменники дробів не рівні один одному, потрібно зробити їх рівними. Випишіть кратні кожного знаменника, щоб знайти число, яке є кратним обох знаменників. Наприклад, дано вираз 1/4-1/5; випишіть всі кратні 4 і 5, щоб знайти, що НОК = 20.[1]- Кратними 4 є 4, 8, 12, 16, 20; кратними 5 є 5, 10, 15, 20. Таким чином, 20-це найменше число, яке є загальним кратним обох знаменників.
- Якщо знаменники рівні один одному, просто відніміть чисельники дробів.
 Помножте чисельник і знаменник на певне число, щоб привести дроби до спільного знаменника. коли ви знайдете НОК, помножте дріб на деяке число, щоб привести дроби до спільного знаменника.[2]
Помножте чисельник і знаменник на певне число, щоб привести дроби до спільного знаменника. коли ви знайдете НОК, помножте дріб на деяке число, щоб привести дроби до спільного знаменника.[2]- У нашому прикладі помножте чисельник і знаменник 1/4 на 5, щоб отримати дріб 5/20.
 Приведіть до спільного знаменника всі дроби виразу. коли ви приведете до спільного знаменника перший дріб, зробіть те ж саме з іншими дробами виразу.[3]
Приведіть до спільного знаменника всі дроби виразу. коли ви приведете до спільного знаменника перший дріб, зробіть те ж саме з іншими дробами виразу.[3]- Наприклад, ви перетворили дріб 1/4 в 5/20. Тепер помножте чисельник і знаменник 1/5 на 4, щоб отримати дріб 4/20. Початковий вираз 1/4 – 1/5 запишеться так: 5/20-4/20.
 ВіднімітьЧисельники, а знаменник не чіпайте. якщо дано дроби з однаковими знаменниками або якщо ви привели дробу до спільного знаменника, відніміть чисельники. Результат запишіть в чисельнику, при цьому знаменник залишиться тим же.[4]
ВіднімітьЧисельники, а знаменник не чіпайте. якщо дано дроби з однаковими знаменниками або якщо ви привели дробу до спільного знаменника, відніміть чисельники. Результат запишіть в чисельнику, при цьому знаменник залишиться тим же.[4]- Запам'ятайте: знаменники не віднімаються.
- Наприклад: 5– - 4/20 = 1/20.
 Скоротіть Отриманий дріб. перевірте, чи можна скоротити отриману дріб. Для цього знайдіть найбільший спільний дільник (НСД) чисельника і знаменника, і розділіть на нього обидва числа. Наприклад, якщо ви отримали дріб 24/32, її НСД = 8. Розділіть чисельник і знаменник на 8, щоб отримати дріб 3/4.[5]
Скоротіть Отриманий дріб. перевірте, чи можна скоротити отриману дріб. Для цього знайдіть найбільший спільний дільник (НСД) чисельника і знаменника, і розділіть на нього обидва числа. Наприклад, якщо ви отримали дріб 24/32, її НСД = 8. Розділіть чисельник і знаменник на 8, щоб отримати дріб 3/4.[5]- Можливо, отриманий дріб скоротити не можна. Наприклад, дріб 1/20 не скорочується.
Метод2 З 2:
Як відняти змішані числа
Метод2 З 2:
 Перетворіть змішані числа в неправильні дроби. змішане число включає ціле число і дріб. Щоб спростити процес віднімання змішаних чисел, перетворіть їх в неправильні дроби (у таких дробів чисельник більше знаменника).[6]
Перетворіть змішані числа в неправильні дроби. змішане число включає ціле число і дріб. Щоб спростити процес віднімання змішаних чисел, перетворіть їх в неправильні дроби (у таких дробів чисельник більше знаменника).[6]- Наприклад, 2 3/4 – 1 1/7 = 11/4 – 8/7.
 Знайдіть спільний знаменник (якщо потрібно). випишіть кратні обох знаменників, щоб знайти їх найменше спільне кратне (НОК). У нашому прикладі 11/4-8/7 випишіть кратні 4 і 7, щоб знайти, що НОК = 28.[7]
Знайдіть спільний знаменник (якщо потрібно). випишіть кратні обох знаменників, щоб знайти їх найменше спільне кратне (НОК). У нашому прикладі 11/4-8/7 випишіть кратні 4 і 7, щоб знайти, що НОК = 28.[7]- Кратними 4 є 4, 8, 12, 16, 20, 24, 28; кратними 7 є 7, 14, 21 і 28. Таким чином, 28-це найменше число, яке є кратним обох знаменників.
 Приведіть дроби до спільного знаменника (якщо потрібно).загальний знаменник дорівнює НОК. Щоб привести дроби до спільного знаменника, помножте кожен дріб на деяке число.[8]
Приведіть дроби до спільного знаменника (якщо потрібно).загальний знаменник дорівнює НОК. Щоб привести дроби до спільного знаменника, помножте кожен дріб на деяке число.[8]- Наприклад, щоб привести дріб 11/4 до знаменника 28, помножте її чисельник і знаменник на 7. Ви отримаєте дріб 77/28.
 Приведіть до спільного знаменника всі дроби виразу. коли ви приведете до спільного знаменника перший дріб, зробіть те ж саме з іншими дробами виразу.[9]
Приведіть до спільного знаменника всі дроби виразу. коли ви приведете до спільного знаменника перший дріб, зробіть те ж саме з іншими дробами виразу.[9]- Наприклад, ви перетворили дріб 11/4 в 77/28. Тепер помножте чисельник і знаменник дробу 8/7 на 4, щоб отримати 32/28. Початковий вираз 11/4 – 8/7 запишеться так: 77/28-32/28.

 Спростіть відповідь. ймовірно, неправильну дріб потрібно перетворити в змішане число. Для цього розділіть чисельник на знаменник-цілий результат ділення буде цілим числом, а залишок від ділення — чисельником дробу; знаменник не зміниться. Якщо можливо, скоротіть дріб.[11]
Спростіть відповідь. ймовірно, неправильну дріб потрібно перетворити в змішане число. Для цього розділіть чисельник на знаменник-цілий результат ділення буде цілим числом, а залишок від ділення — чисельником дробу; знаменник не зміниться. Якщо можливо, скоротіть дріб.[11]- Наприклад, 45/28 = 1 17/28, тому що 45/28 = 1 ост. 17.
Поради
- Якщо хочете, віднімайте змішані числа, не перетворюючи їх в неправильні дроби. Для цього відніміть цілі числа, а потім відніміть чисельники дробів, якщо у них спільний знаменник.
Джерела
- ↑ Https://www.georgebrown.ca/uploadedFiles/TLC/_documents/Adding%20and%20Subtracting%20Proper%20Fractions.pdf
- ↑ Https://www.georgebrown.ca/uploadedFiles/TLC/_documents/Adding%20and%20Subtracting%20Proper%20Fractions.pdf
- ↑ Https://www.georgebrown.ca/uploadedFiles/TLC/_documents/Adding%20and%20Subtracting%20Proper%20Fractions.pdf
- ↑ Https://www.georgebrown.ca/uploadedFiles/TLC/_documents/Adding%20and%20Subtracting%20Proper%20Fractions.pdf
- ↑ Https://www.georgebrown.ca/uploadedFiles/TLC/_documents/Adding%20and%20Subtracting%20Proper%20Fractions.pdf
- ↑ Https://www.georgebrown.ca/uploadedFiles/TLC/_documents/Adding%20and%20Subtracting%20Mixed%20Numbers%20and%20Improper%20Fractions.pdf
- ↑ Https://www.georgebrown.ca/uploadedFiles/TLC/_documents/Adding%20and%20Subtracting%20Mixed%20Numbers%20and%20Improper%20Fractions.pdf
- ↑ Https://www.georgebrown.ca/uploadedFiles/TLC/_documents/Adding%20and%20Subtracting%20Mixed%20Numbers%20and%20Improper%20Fractions.pdf
- ↑ Https://www.georgebrown.ca/uploadedFiles/TLC/_documents/Adding%20and%20Subtracting%20Mixed%20Numbers%20and%20Improper%20Fractions.pdf