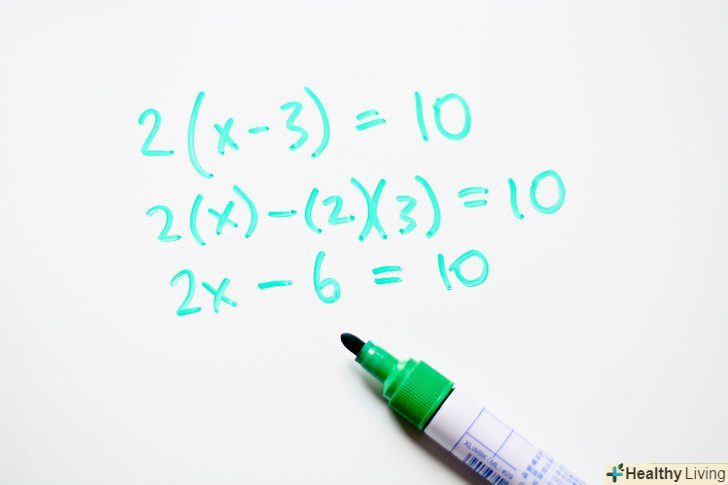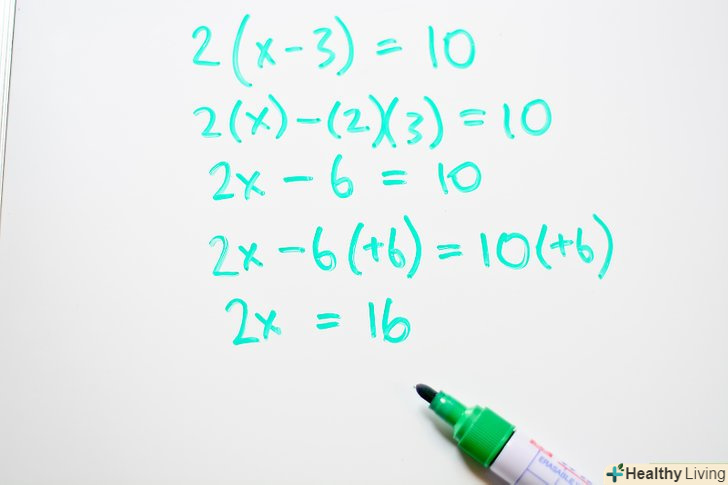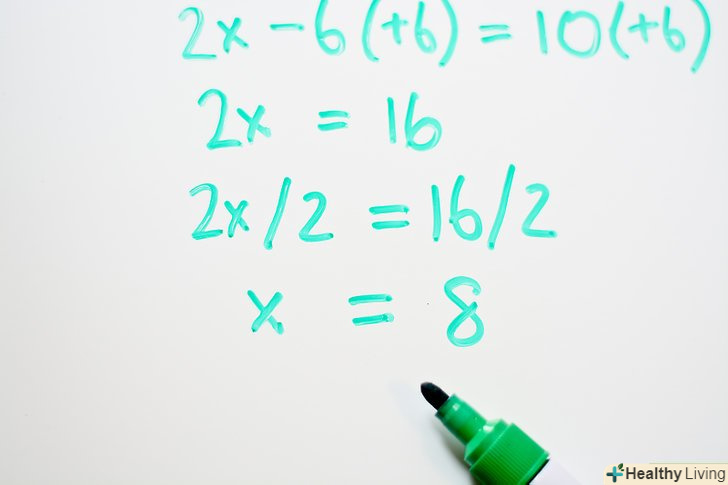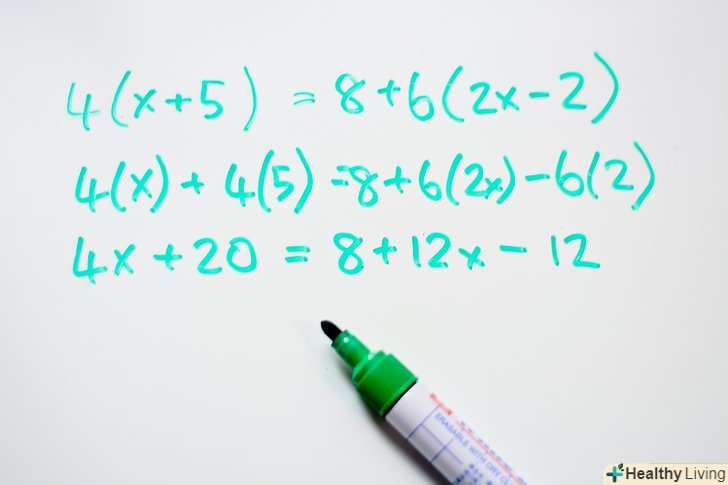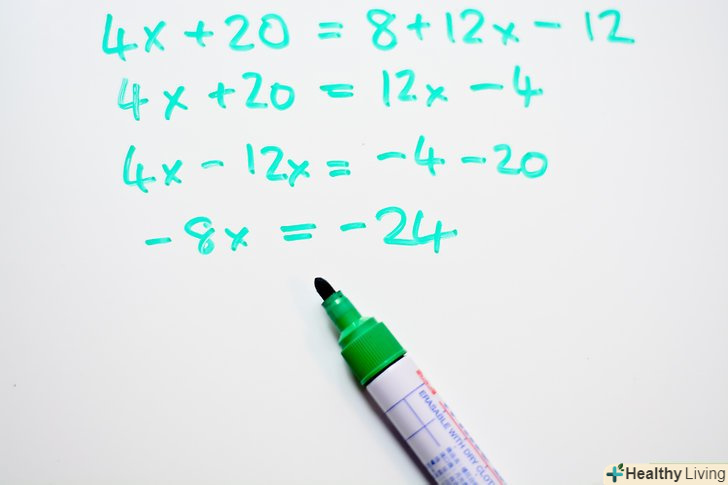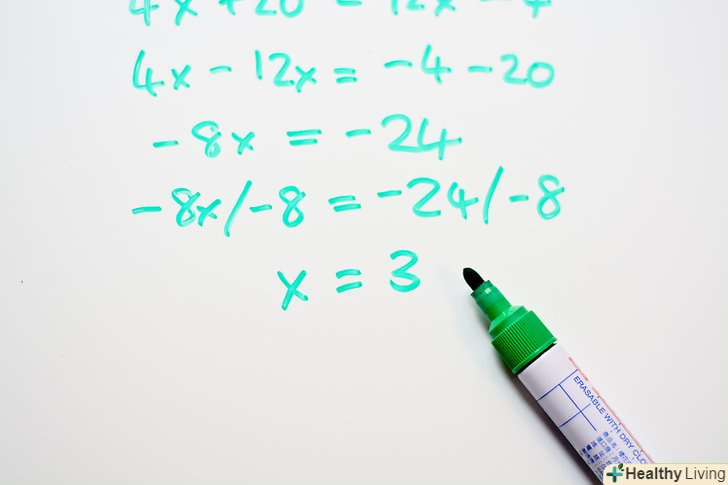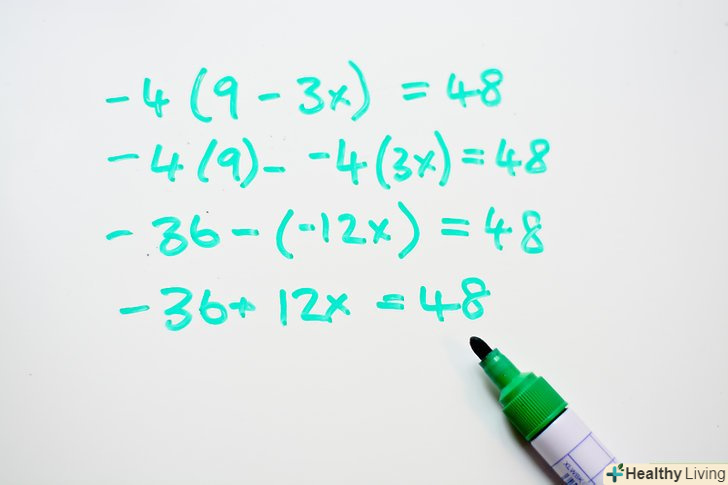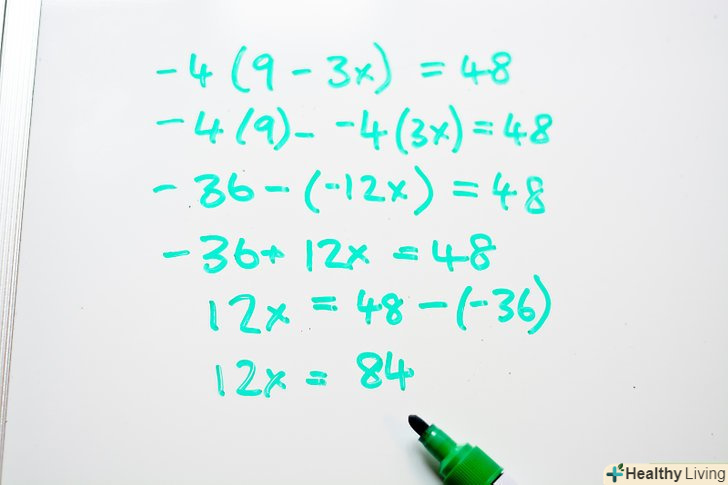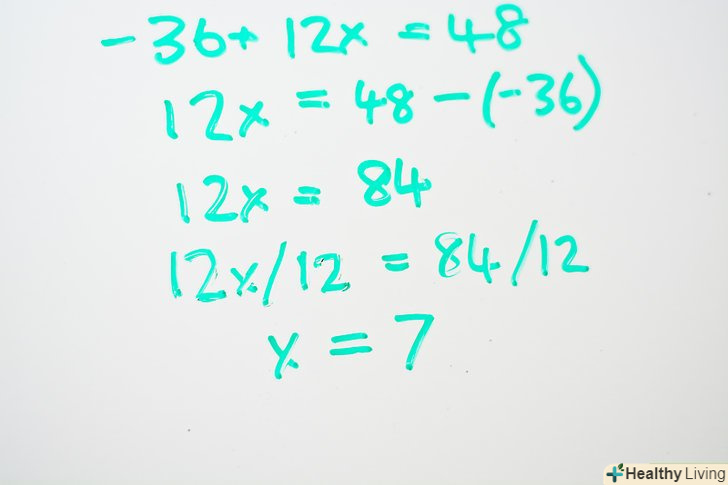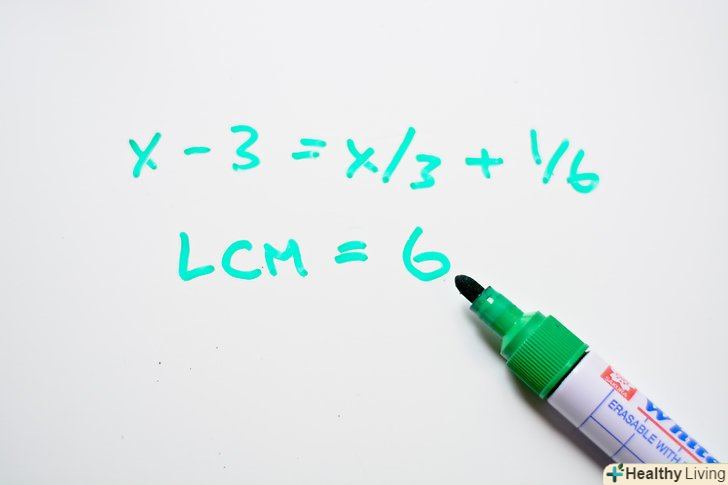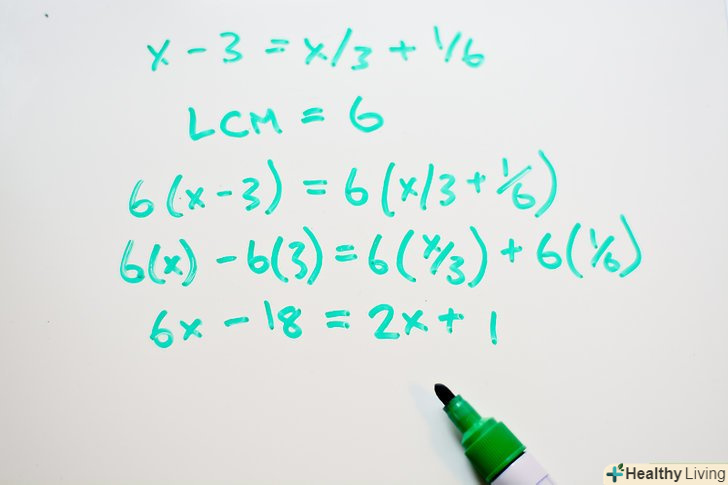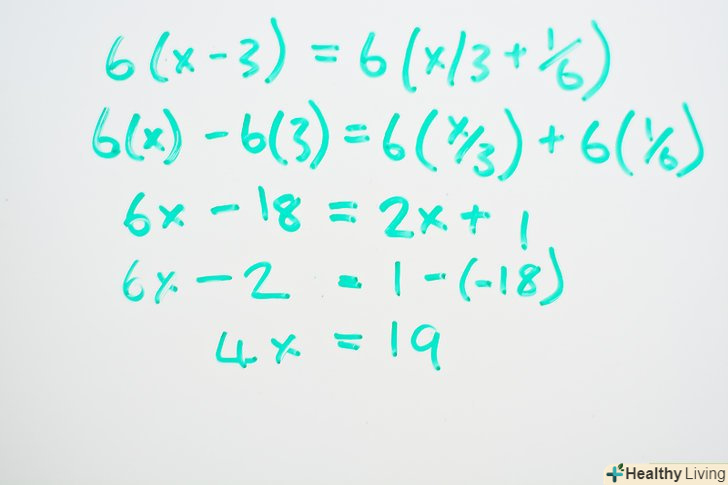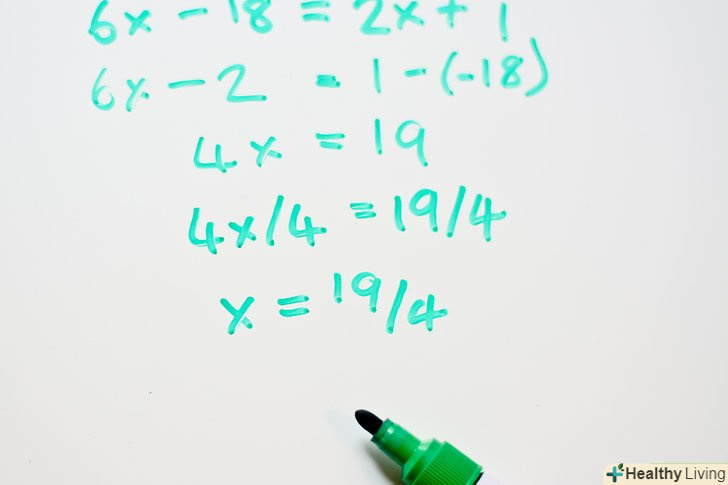Дистрибутивність (властивість дистрибутивності, розподільний закон) говорить, що добуток числа і суми чисел дорівнює сумі добутку числа і окремих доданків. Це означає, Що a (b + c) = ab + ac. Ви можете використовувати цю основну властивість при вирішенні та спрощенні різноманітних рівнянь. Якщо ви хочете знати, як використовувати властивість дистрибутивності при вирішенні рівняння, дотримуйтесь цих кроків.
Кроки
Метод1З 4:
Використовуємо основну властивість дистрибутивності
Метод1З 4:
 Перемножьте число (член) за дужками і числа (члени) в дужках.помножте число за дужками на перший доданок в дужках, а потім помножте його на другий доданок. Якщо доданків більше ніж два, помножте число за дужками на всі доданки в дужках.[1] Ось як це зробити:
Перемножьте число (член) за дужками і числа (члени) в дужках.помножте число за дужками на перший доданок в дужках, а потім помножте його на другий доданок. Якщо доданків більше ніж два, помножте число за дужками на всі доданки в дужках.[1] Ось як це зробити:- Наприклад: 2 (x - 3) = 10
- 2(x) - (2)(3) = 10
- 2x - 6 = 10
 Складіть подібні члени.перш ніж приступити до вирішення рівняння, необхідно скласти подібні члени. Складіть всі вільні члени і члени зі змінною "х". Перенесіть всі вільні члени на одну сторону рівняння, а члени з невідомим – на іншу.
Складіть подібні члени.перш ніж приступити до вирішення рівняння, необхідно скласти подібні члени. Складіть всі вільні члени і члени зі змінною "х". Перенесіть всі вільні члени на одну сторону рівняння, а члени з невідомим – на іншу.- 2x - 6(+6) = 10 (+6)
- 2x = 16
 Вирішіть рівняння. знайдіть "х", розділивши обидві частини рівняння на 2.
Вирішіть рівняння. знайдіть "х", розділивши обидві частини рівняння на 2.- 2x = 16
- 2x/2 = 16/2
- X = 8
Метод2З 4:
Використовуємо властивість дистрибутивності. Більш складне завдання
Метод2З 4:
 Перемножьте число за дужками і числа в дужках. це робиться так само, як у попередньому розділі, але тут ми будемо використовувати властивість дистрибутивності більше одного разу.
Перемножьте число за дужками і числа в дужках. це робиться так само, як у попередньому розділі, але тут ми будемо використовувати властивість дистрибутивності більше одного разу.- Наприклад: 4 (x + 5) = 8 + 6 (2x-2)
- 4(x) + 4(5) = 8 + 6(2x) - 6(2)
- 4x + 20 = 8 +12x -12
 Складіть подібні члени. перенесіть всі вільні члени на одну сторону рівняння, а члени з невідомим – на іншу.
Складіть подібні члени. перенесіть всі вільні члени на одну сторону рівняння, а члени з невідомим – на іншу.- 4x + 20 = 8 +12x -12
- 4x + 20 = 12x - 4
- 4x -12x = -4 - 20
- -8x = -24
 Вирішіть рівняння. знайдіть "х", розділивши обидві частини рівняння на -8.
Вирішіть рівняння. знайдіть "х", розділивши обидві частини рівняння на -8.- -8x/-8 = -24/-8
- X = 3
Метод3З 4:
Дистрибутивность при негативних коефіцієнтах
Метод3З 4:
 Перемножьте число за дужками і числа в дужках.якщо це число-негативне, то дійте згідно з правилами операцій з негативними числами. Якщо ви множите негативне число на позитивне, то результат негативний; якщо ви множите негативне число на інше негативне число, то результат буде позитивним.[2]
Перемножьте число за дужками і числа в дужках.якщо це число-негативне, то дійте згідно з правилами операцій з негативними числами. Якщо ви множите негативне число на позитивне, то результат негативний; якщо ви множите негативне число на інше негативне число, то результат буде позитивним.[2]- Наприклад: -4 (9 - 3x) = 48
- -4(9) - -4(3x) = 48
- -36 -(-12x) = 48
- -36 + 12x = 48
 Складіть подібні члени. перенесіть всі вільні члени на одну сторону рівняння, а члени з невідомим – на іншу.
Складіть подібні члени. перенесіть всі вільні члени на одну сторону рівняння, а члени з невідомим – на іншу.- -36 + 12x = 48
- 12x = 48 - -(36)
- 12x = 84
 Вирішіть рівняння. знайдіть "х", розділивши обидві частини рівняння на 12.
Вирішіть рівняння. знайдіть "х", розділивши обидві частини рівняння на 12.- 12x/12 = 84/12
- X = 7
Метод4З 4:
Спрощення рівняння
Метод4З 4:
 Знайти найменше спільне кратне (НОК) для знаменників дробів у рівнянні.для знаходження найменшого загального кратного двох чисел просто знайдіть найменше число, яке ділиться на обидва цих числа. Числа в знаменниках 3 і 6, і 6 - найменше число, яке ділиться на 3 і на 6.[3]
Знайти найменше спільне кратне (НОК) для знаменників дробів у рівнянні.для знаходження найменшого загального кратного двох чисел просто знайдіть найменше число, яке ділиться на обидва цих числа. Числа в знаменниках 3 і 6, і 6 - найменше число, яке ділиться на 3 і на 6.[3]- X - 3 = x/3 + 1/6
- НОК = 6
 Помножте всі члени рівняння на НОК.тепер укладіть в дужки всі члени вихідного рівняння (на кожній стороні рівняння) і поставте НОК за дужками. Потім перемножте НОК і доданки в дужках. Множення обох частин рівняння на одне і те ж число не змінює кінцевого результату рівняння, але призведе до виду рівняння без дробів.
Помножте всі члени рівняння на НОК.тепер укладіть в дужки всі члени вихідного рівняння (на кожній стороні рівняння) і поставте НОК за дужками. Потім перемножте НОК і доданки в дужках. Множення обох частин рівняння на одне і те ж число не змінює кінцевого результату рівняння, але призведе до виду рівняння без дробів.- 6(x - 3) = 6(x/3 + 1/6)
- 6(x) - 6(3) = 6(x/3) + 6(1/6)
- 6x - 18 = 2x + 1
 Складіть подібні члени. перенесіть всі вільні члени на одну сторону рівняння, а члени з невідомим – на іншу.
Складіть подібні члени. перенесіть всі вільні члени на одну сторону рівняння, а члени з невідомим – на іншу.- 6x - 2x = 1 - (-18)
- 4x = 19
 Вирішіть рівняння. знайдіть "х", розділивши обидві частини рівняння на 4.
Вирішіть рівняння. знайдіть "х", розділивши обидві частини рівняння на 4.- 4x/4 = 19/4
- X = 19/4 or 16 3/4