1. Головна
    2. Математика
    3. Як вивчати тригонометрію-

Як вивчати тригонометрію-

Тригонометрія-це розділ математики, в якому вивчаються тригонометричні функції та їх використання в геометрії. Тригонометричні функції використовуються для опису властивостей різних кутів, трикутників і періодичних функцій. Вивчення тригонометрії допоможе вам зрозуміти ці властивості. Заняття в школі і Самостійна робота допоможуть вам засвоїти основи тригонометрії і зрозуміти багато періодичні процеси.

Метод1З 4:
Вивчіть основи тригонометрії

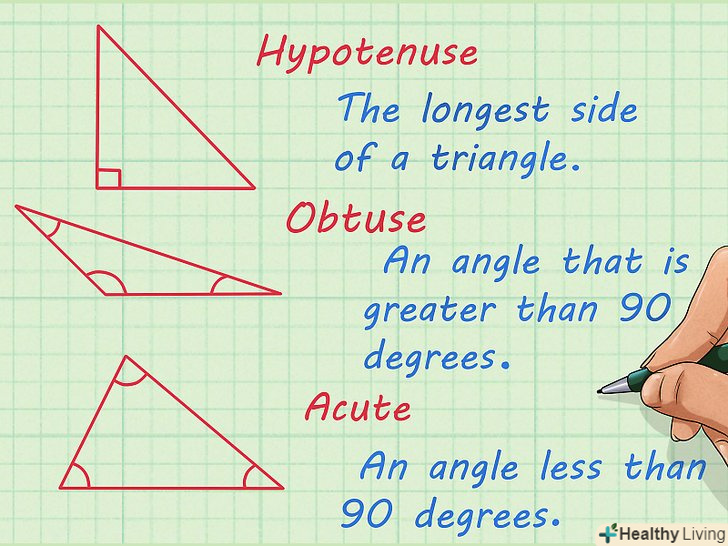
  1. Ознайомтеся з поняттям трикутника.по суті, тригонометрія займається вивченням різних співвідношень в трикутниках. Трикутник має три сторони і три кути. Сума кутів будь-якого трикутника становить 180 градусів. При вивченні тригонометрії необхідно ознайомитися з трикутниками і пов'язаними з ними поняттями, такими як:[1]
    • Гіпотенуза-найдовша сторона прямокутного трикутника;
    • Тупий кут-кут більше 90 градусів;
    • Гострий кут-кут менше 90 градусів.
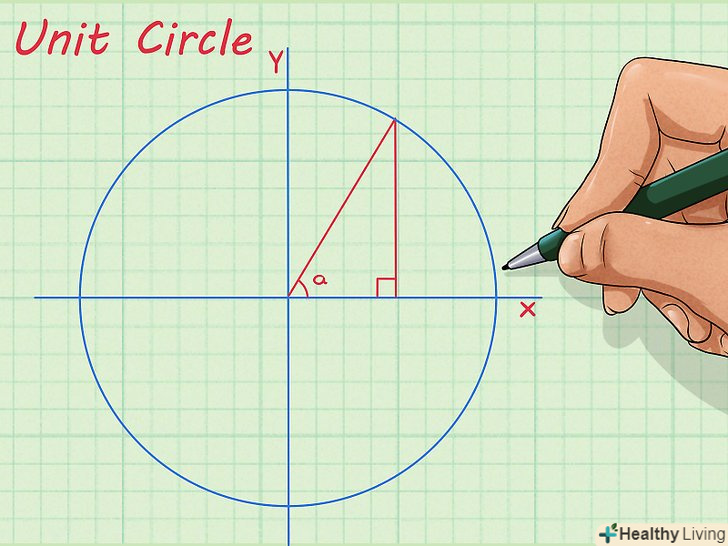
  2. Навчіться будувати одиничну окружність.одинична окружність дає можливість побудувати будь-який прямокутний трикутник так, щоб гіпотенуза дорівнювала одиниці. Це зручно при роботі з тригонометричними функціями, такими як синус і косинус. Освоївши одиничну окружність, ви легко зможете знаходити значення тригонометричних функцій для певних кутів і вирішувати завдання, в яких фігурують трикутники з цими кутами.[2]
    • Приклад 1. Синус кута величиною 30 градусів становить 0,50. Це означає, що довжина протилежного куту катета дорівнює половині довжини гіпотенузи.
    • Приклад 2. За допомогою даного співвідношення можна обчислити довжину гіпотенузи трикутника, в якому є кут величиною 30 градусів, а довжина протилежного цьому куту катета дорівнює 7 сантиметрам. В цьому випадку довжина гіпотенузи складе 14 сантиметрів.
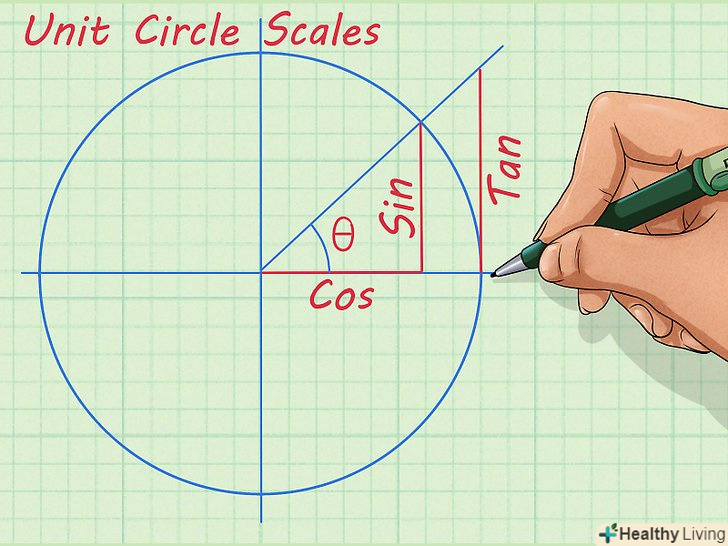
  3. Ознайомтеся з тригонометричними функціями.існує шість основних тригонометричних функцій, які необхідно знати при вивченні тригонометрії. Ці функції являють собою співвідношення між різними сторонами прямокутного трикутника і допомагають зрозуміти властивості будь-якого трикутника. Ось ці шість функцій: [3]
    • Синус (sin);
    • Косинус (cos);
    • Тангенс (tg);
    • Секанс (sec);
    • Косеканс (cosec);
    • Котангенс (ctg).
  4. Запам'ятайте співвідношення між функціями.при вивченні тригонометрії вкрай важливо розуміти, що всі тригонометричні функції пов'язані між собою. Хоча синус, косинус, тангенс і інші функції використовуються по-різному, вони знаходять широке застосування завдяки тому, що між ними існують певні співвідношення. Ці співвідношення легко зрозуміти за допомогою одиничного кола. Навчіться користуватися одиничною окружністю, і за допомогою описуваних нею співвідношень ви зможете вирішувати багато завдань.[4]

Метод2З 4:
Застосування тригонометрії

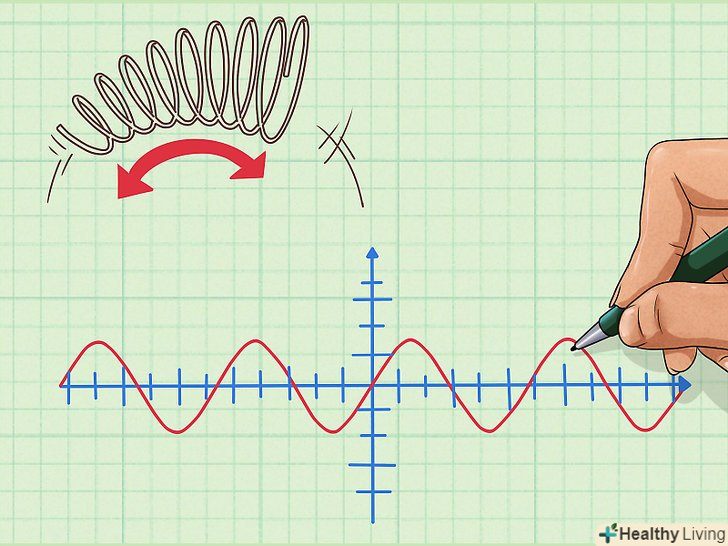
  1. Дізнайтеся про основні галузі науки, в яких використовується тригонометрія.Тригонометрія корисна в багатьох розділах математики та інших точних наук. За допомогою тригонометрії можна знайти величини кутів і прямих відрізків. Крім того, тригонометричними функціями можна описати будь-який циклічний процес.[5]
    • Наприклад, коливання пружини можна описати синусоїдальною функцією.
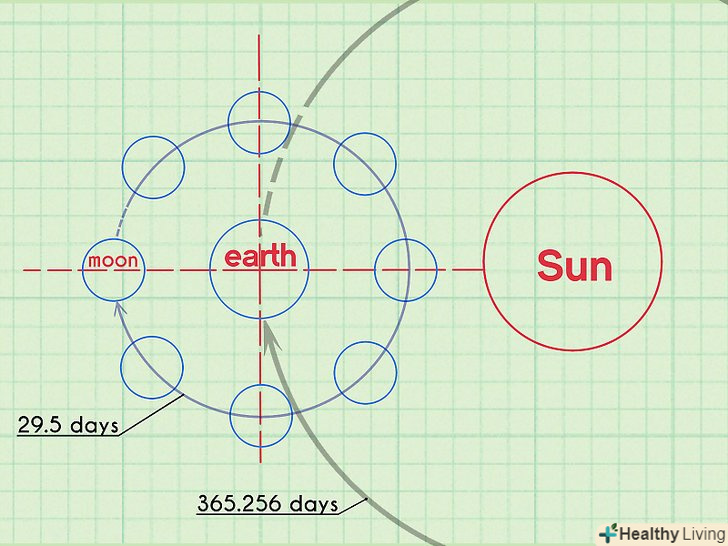
  2. Подумайте про періодичні процеси.іноді абстрактні поняття математики та інших точних наук важкі для розуміння. Тим не менш, вони присутні в навколишньому світі, і це може полегшити їх розуміння. Придивіться до періодичних явищ навколо вас і спробуйте зв'язати їх з тригонометрією.[6]
    • Місяць має передбачуваний цикл, тривалість якого становить близько 29,5 дня.
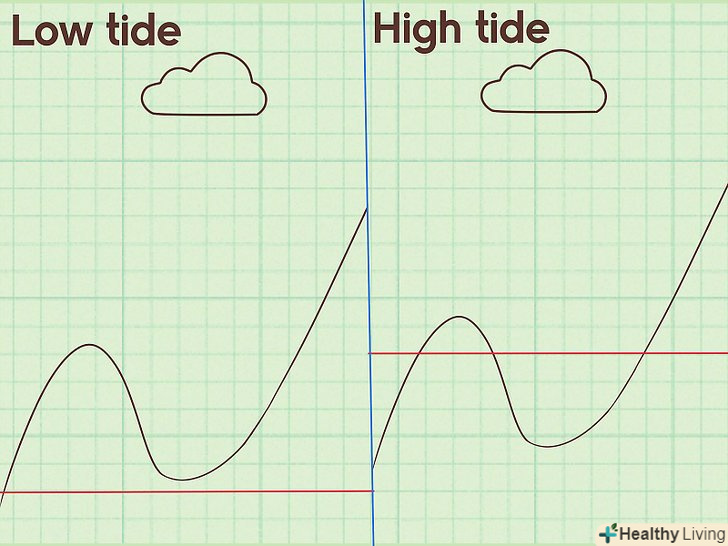
  3. Уявіть собі, як можна вивчати природні цикли.коли ви зрозумієте, що в природі протікає безліч періодичних процесів, подумайте про те, як можна вивчати ці процеси. Подумки уявіть, як виглядає зображення таких процесів на графіку. За допомогою графіка можна скласти рівняння, яке описує спостережуване явище. При цьому вам знадобляться тригонометричні функції.[7]
    • Уявіть собі припливи і відливи на березі моря. Під час припливу вода піднімається до певного рівня, а потім настає відплив, і рівень води падає. Після відливу знову слід приплив, і рівень води піднімається. Цей циклічний процес може тривати нескінченно. Його можна описати тригонометричною функцією, наприклад косинусом.

Метод3З 4:
Вивчайте матеріал заздалегідь

  1. Прочитайте відповідний розділ.деяким людям важко засвоїти ідеї тригонометрії з першого разу. Якщо ви ознайомитеся з відповідним матеріалом перед заняттями, то краще засвоїте його. Намагайтеся частіше повторювати досліджуваний предмет-таким чином ви виявите більше взаємозв'язків між різними поняттями і концепціями тригонометрії.[8]
    • Крім того, це дозволить вам заздалегідь виявити неясні моменти.
  2. Ведіть конспект.хоча побіжний перегляд підручника краще, ніж нічого, при вивченні тригонометрії необхідно неспішне вдумливе читання. При вивченні будь-якого розділу ведіть докладний конспект. Пам'ятайте, що знання тригонометрії накопичується поступово, і новий матеріал спирається на вивчений раніше, тому записи вже пройденого допоможуть вам просунутися далі.[9]
    • Крім іншого, записуйте виникли у вас питання, щоб потім задати їх вчителю.
  3. Вирішуйте наведені в підручнику завдання.навіть якщо вам легко дається тригонометрія, необхідно вирішувати завдання. Щоб переконатися, що ви дійсно зрозуміли вивчений матеріал, спробуйте перед заняттями вирішити кілька завдань. Якщо при цьому у вас виникнуть проблеми, ви визначите, що саме вам потрібно з'ясувати під час занять.[10]
    • У багатьох підручниках в кінці наведені відповіді до завдань. З їх допомогою можна перевірити, чи правильно ви вирішили завдання.
  4. Беріть на заняття все необхідне.не забувайте свій конспект і вирішення завдань. Ці підручні матеріали допоможуть вам освіжити в пам'яті вже пройдене і просунутися далі у вивченні матеріалу. Прояснюйте також всі питання, які виникли у вас при попередньому читанні підручника.

Метод4З 4:
Ведіть конспект

  1. Записуйте все в один конспект.різні розділи тригонометрії тісно пов'язані між собою. Найкраще записувати все в одному місці, щоб ви могли в будь-який момент освіжити в пам'яті раніше пройдений матеріал. Відведіть для записів окремий зошит або папку.[11]
    • В конспект можна записувати також рішення задач.
  2. Будьте уважні під час занять.не відволікайтеся на спілкування з товаришами або на виконання домашнього завдання з іншого предмету. Приділяйте всю свою увагу викладається предмету і завданням. Заносите в конспект всю важливу інформацію і те, що вчитель пише на дошці.
  3. Проявляйте ініціативу.Викликайтеся до дошки вирішувати завдання і відповідайте на питання, які задає вчитель. Задавайте питання самі, якщо вам що-небудь неясно. Обговорюйте досліджуваний матеріал з учителем і однокласниками (в рамках дозволеного). Це полегшить процес навчання і зробить його більш приємним.
    • Якщо вчитель вважає за краще, щоб його не перебивали, можна задати йому питання після занять. Не соромтеся: робота вчителя полягає в тому, щоб допомогти Вам у вивченні тригонометрії.
  4. Намагайтеся вирішувати більше завдань. Виконуйте всі домашні завдання. Домашня робота допомагає краще засвоїти пройдений матеріал. Перевірте, чи все вам зрозуміло. Якщо вчитель нічого не поставив додому, відкрийте підручник і порішайте завдання по останній пройденої теми.[12]

Поради

  • Пам'ятайте про те, що вивчення математики полягає в засвоєнні певного способу мислення, а не тільки в запам'ятовуванні формул.
  • Перед вивченням тригонометрії освіжіть в пам'яті основи алгебри і геометрії.

Попередження

  • Тригонометрію не можна вивчити шляхом автоматичного запам'ятовування. Необхідно розуміти основні ідеї і методи.
  • Проста зубріння неефективна при вивченні тригонометрії.

Джерела

  1. ↑ Http://www.dummies.com/education/math/trigonometry/trigonometry-for-dummies-cheat-sheet/
  2. ↑ Http://www.mathsisfun.com/algebra/trigonometry.html
  3. ↑ Http://www.dummies.com/education/math/trigonometry/trigonometry-for-dummies-cheat-sheet/
  4. ↑ Http://www.mathsisfun.com/algebra/trigonometry.html
  5. ↑ Https://betterexplained.com/articles/intuitive-trigonometry/
  6. ↑ Https://betterexplained.com/articles/intuitive-trigonometry/
  7. ↑ Https://betterexplained.com/articles/intuitive-trigonometry/
  8. ↑ Http://getcollegecredit.com/blog/article/10_math_study_tips_that_will_make_you_a_better_student
  9. ↑ Http://getcollegecredit.com/blog/article/10_math_study_tips_that_will_make_you_a_better_student
  1. ↑ Http://getcollegecredit.com/blog/article/10_math_study_tips_that_will_make_you_a_better_student
  2. ↑ Http://getcollegecredit.com/blog/article/10_math_study_tips_that_will_make_you_a_better_student
  3. ↑ Http://getcollegecredit.com/blog/article/10_math_study_tips_that_will_make_you_a_better_student

Ще почитати: