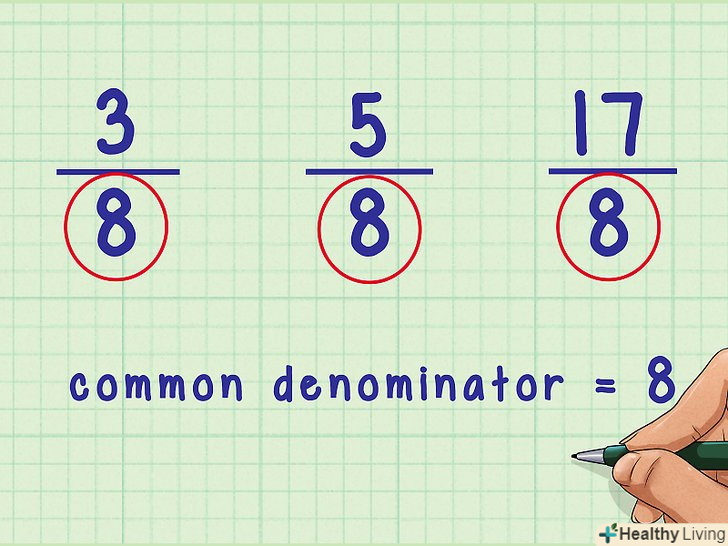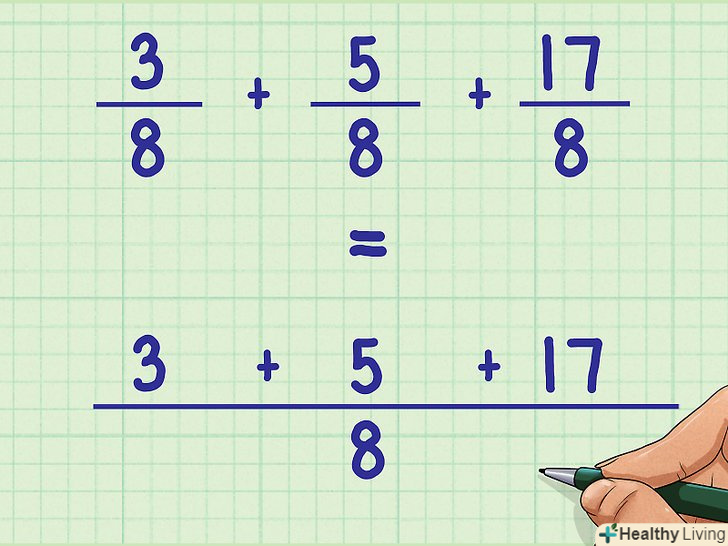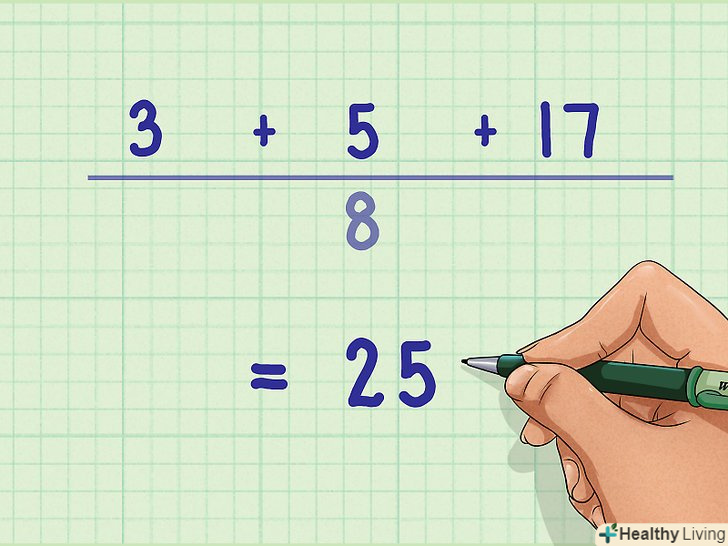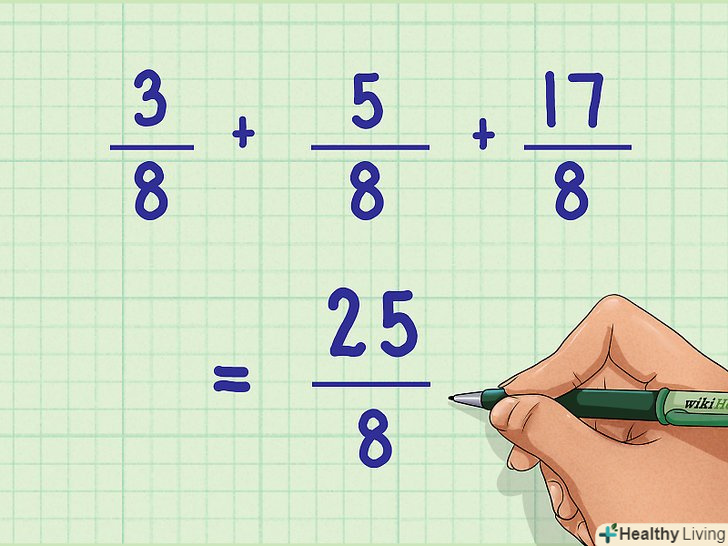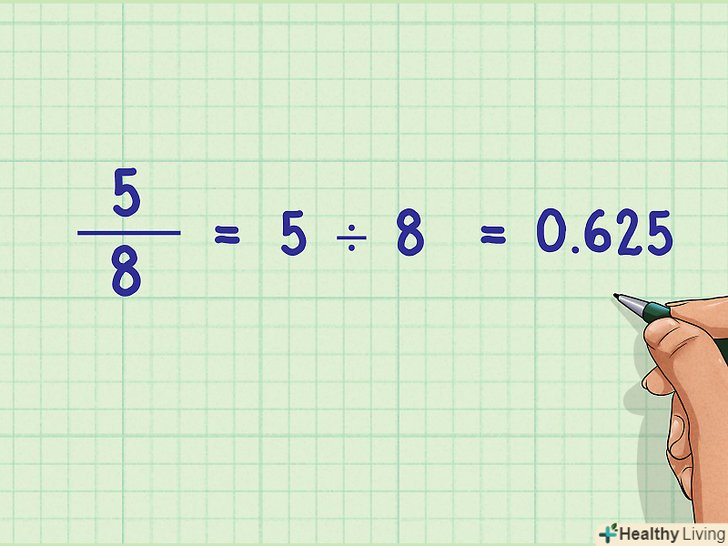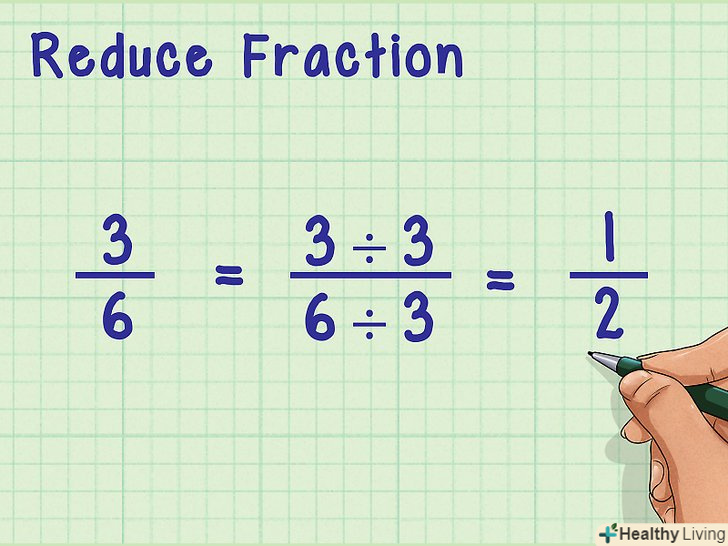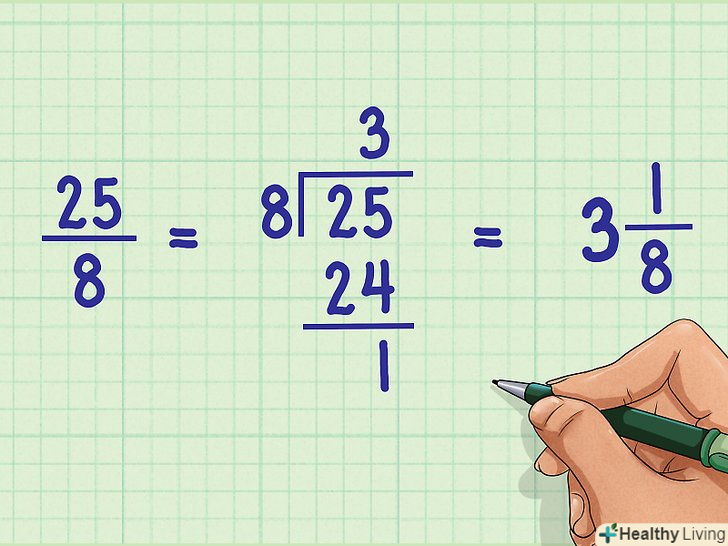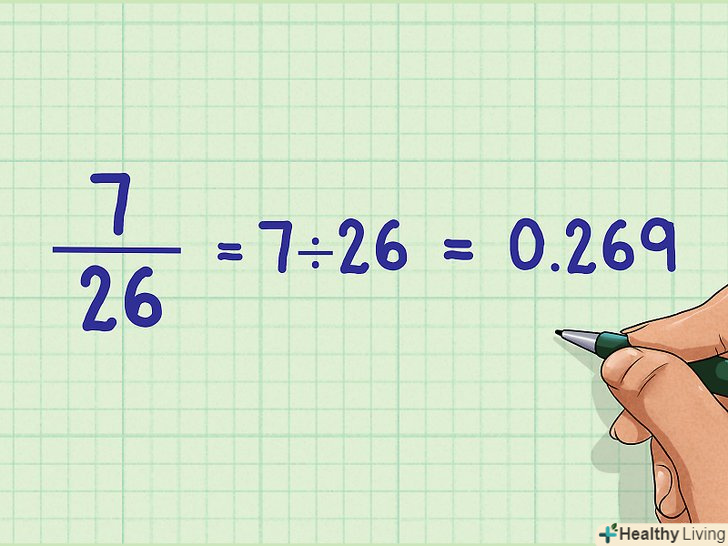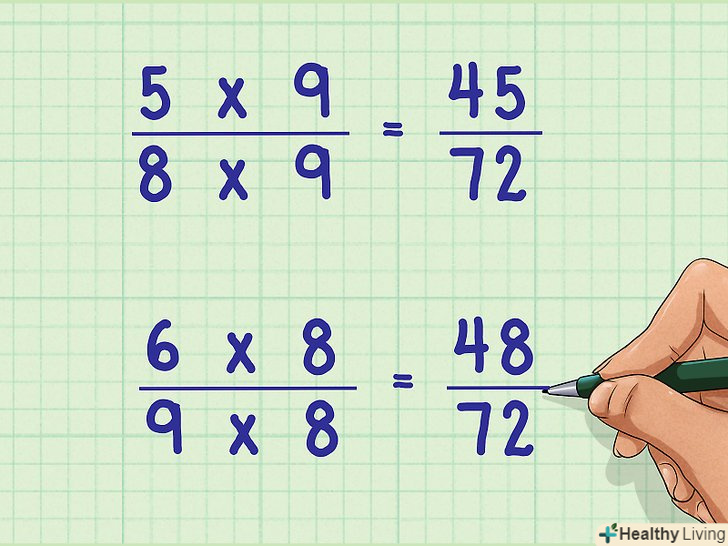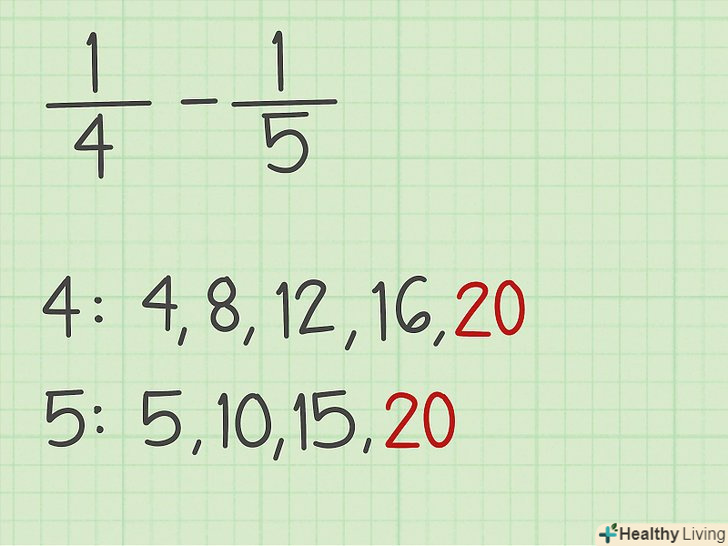1. Головна
    2. Математика
    3. Як складати дроби з однаковими знаменниками

Як складати дроби з однаковими знаменниками

Дріб складається з чисельника і знаменника. Коли у дробів однакові знаменники, кажуть, що у дробів спільний знаменник. Дроби із загальним знаменником дуже легко складати, тому що в цьому випадку потрібно просто скласти чисельники! Знаменник сумарного дробу буде таким же, як у вихідних дробів, тому потрібно скласти числа, які знаходяться над рисою. Аналогічне правило застосовується при відніманні дробів з однаковим знаменником. Завдання ускладнюється, коли у дробів різні знаменники, але якщо знайти спільний знаменник, можна запросто складати і віднімати такі дроби.

Частина1З 3:
Додавання дробів із загальним знаменником

  1. Знайдіть чисельник і знаменник.дріб складається з двох частин: число, яке розташоване над рисою, називається чисельником, а число, яке знаходиться під рисою, — знаменником. Знаменник позначає загальну кількість частин, на які розбито деяке ціле, а чисельник — це розглядається кількість таких частин.[1]
    • Наприклад, у дробу ½ чисельником є 1, а знаменником 2.
  2. Визначте знаменник. якщо два дроби і більше мають спільний знаменник, у таких дробів під рисою знаходиться одне і те ж число, тобто в цьому випадку деяке ціле розбите на однакову кількість частин. Складати дроби із загальним знаменником дуже просто, так як знаменник сумарної дробу буде таким же, як у складаються дробів. Наприклад:
    • У дробів 3/5 і 2/5 спільний знаменник 5.
    • У дробів 3/8, 5/8, 17/8 спільний знаменник 8.
  3. Визначте чисельники. щоб скласти дроби із загальним знаменником, складіть їх чисельники, а результат запишіть над знаменником складаються дробів.[2]
    • У дробів 3/5 і 2/5 чисельники 3 і 2.
    • У дробів 3/8, 5/8, 17/8 чисельники 3, 5, 17.
  4. Складіть чисельники.у прикладі 3/5 + 2/5 складіть чисельники 3 + 2 = 5. У прикладі 3/8 + 5/8 + 17/8 складіть чисельники 3 + 5 + 17 = 25.
  5. Запишіть сумарний дріб.Пам'ятайте, що при додаванні дробів із загальним знаменником він залишається без змін-складаються тільки чисельники.
    • 3/5 + 2/5 = 5/5
    • 3/8 + 5/8 + 17/8 = 25/8
  6. Якщо потрібно, Перетворіть дріб.іноді дріб можна записати у вигляді цілого числа, а не звичайного або десяткового дробу. Наприклад, дріб 5/5 легко перетворюється в 1, так як будь-яка дріб, у якій чисельник дорівнює знаменнику, є 1.[3] уявіть пиріг, розрізаний на три частини. Якщо ви з'їсте всі три частини, то ви з'їсте цілий (один) пиріг.
    • Будь-яку звичайну дріб можна перетворити в десяткову; для цього розділіть чисельник на знаменник. Наприклад, дріб 5/8 можна записати так: 5 ÷ 8 = 0,625.
  7. Якщо можливо, спростіть дріб.спрощена дріб-цей дріб, чисельник і знаменник якої не мають спільних дільників.[4]
    • Наприклад, розглянемо дріб 3/6. Тут і у чисельника, і у знаменника є загальний дільник, рівний 3, тобто чисельник і знаменник націлено діляться на 3. Тому дріб 3/6 можна записати так: (3 ÷ 3) / (6 ÷ 3) = ½ .
  8. Якщо потрібно, Перетворіть неправильну дріб в змішану дріб (змішане число). у неправильної дробу чисельник більше знаменника, наприклад, 25/8 (у правильної дробу чисельник менше знаменника). Неправильну дріб можна перетворити в змішану дріб, яка складається з цілої частини (тобто цілого числа) і дробової частини (тобто правильної дробу). Щоб перетворити неправильну дріб, наприклад, 25/8, в змішане число, виконайте наступні дії:[5]
    • Розділіть чисельник неправильного дробу на її знаменник; запишіть неповне ПРИВАТНЕ (ціла відповідь). У нашому прикладі: 25 ÷ 8 = 3 плюс деякий залишок. В даному випадку ціла відповідь - це ціла частина змішаного числа.
    • Знайдіть залишок. У нашому прикладі: 8 х 3 = 24; отриманий результат відніміть з вихідного чисельника: 25 – 24 = 1, тобто залишок дорівнює 1. В даному випадку залишок-це чисельник дробової частини змішаного числа.
    • Запишіть змішаний дріб. Знаменник не змінюється (тобто дорівнює знаменнику неправильного дробу), тому 25/8 = 3 1/8.

Частина2З 3:
Віднімання дробів із загальним знаменником

  1. Знайдіть чисельники і знаменники.розглянемо приклад 12/26 – 4/26 – 1/26. Тут:
    • Чисельники 12, 4, 1
    • Загальний знаменник 26
  2. Відніміть чисельники.оскільки знаменник не змінюється, просто знайдіть різницю чисельників:
    • 12 – 4 – 1 = 7
    • Запишіть дріб з новим чисельником: 12/26 – 4/26 – 1/26 = 7/26.
  3. Якщо потрібно, спростіть або Перетворіть дріб. дії з кінцевим дробом при відніманні дробів аналогічні діям з сумарним дробом:
    • Неправильну дріб можна перетворити в змішане число (змішаний дріб).
    • Звичайний дріб можна перетворити в десяткову або ціле число; для цього розділіть чисельник на знаменник.
    • Дріб можна спростити, якщо у чисельника і знаменника є спільний дільник.

Частина3З 3:
Обчислення спільного знаменника

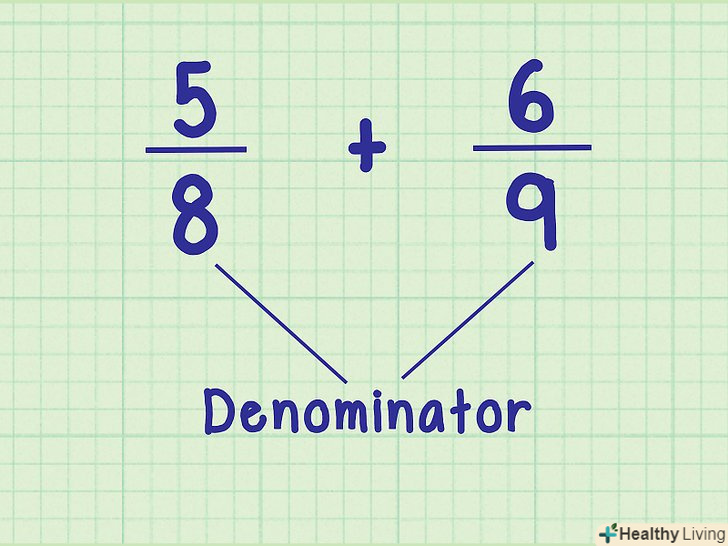
  1. Знайдіть знаменники.у більшості випадків у дробів різні знаменники, тому для того щоб скласти або відняти такі дроби, потрібно обчислити спільний знаменник. Спочатку знайдіть знаменники даних дробів.
    • Наприклад, в задачі 5/8 + 6/9 знаменники — це числа 8 і 9.
  2. Знайдіть найменше спільне кратне (НОК).загальний знаменник дорівнює найменшому загальному кратному двох знаменників, тобто такому числу, яке ділиться на кожен знаменник.[6] щоб знайти НОК чисел 8 і 9, запишіть кратні числа 8, а потім кратні числа 9:
    • Кратні 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, 104 і так далі
    • Кратні 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99, 108 і так далі
    • Найменшим загальним кратним чисел 8 і 9 є число 72.
  3. Приведіть кожен дріб до спільного знаменника.для цього помножте і чисельник, і знаменник кожного дробу на певні числа:
    • Дріб 5/8. Щоб привести цей дріб до спільного знаменника, помножте знаменник (8) на 9: 8 х 9 = 72. Тому чисельник (5) теж помножте на 9: 5 х 9 = 45.
    • Дріб 6/9. Щоб привести цей дріб до спільного знаменника, помножте знаменник (9) на 8: 9 х 8 = 72. Тому чисельник (6) теж помножте на 8: 6 х 8 = 48.[7]
  4. Перепишіть дроби в новому вигляді (із загальним знаменником).У нових дробів буде спільний знаменник, а чисельники рівні добутку вихідних чисельників на певні числа.
    • Таким чином, 5/8 = 45/72 і 6/9 = 48/72.
    • Тепер у дробів спільний знаменник, і їх можна скласти: 45/72 + 48/72 = 93/72.
    • Якщо потрібно або можна, спростіть дріб або Перетворіть її в десяткову або змішану дріб.

Джерела

  1. ↑ Http://www.quickanddirtytips.com/education/math/what-are-numerators-and-denominators?page=1
  2. ↑ Https://www.khanacademy.org/math/arithmetic/fractions/Adding_and_subtracting_fractions/e/adding_fractions_with_common_denominators
  3. ↑ Http://www.mathgoodies.com/lessons/fractions/equivalent.html
  4. ↑ Https://www.mathsisfun.com/definitions/common-factor.html
  5. ↑ Https://www.youtube.com/watch?v=-imFslMIN1g
  6. ↑ Https://www.mathsisfun.com/least-common-multiple.html
  7. ↑ Https://www.khanacademy.org/math/pre-algebra/fractions-pre-alg/fractions-unlike-denom-pre-alg/v/subtracting-fractions-with-unlike-denominators

Ще почитати: