Людині, не знайомому з використанням логарифмічної лінійки, вона здасться роботою Пікассо. Вона має як мінімум три різних шкали, майже на кожній з яких цифри розташовані навіть не на однаковій відстані один від одного. Але розібравшись, що до чого, ви зрозумієте, чому логарифмічна лінійка була такою зручною за часів до винаходу кишенькових калькуляторів. Правильно розташувавши потрібні цифри на шкалі, ви зможете виконати множення двох будь-яких чисел набагато швидше, ніж виконуючи розрахунки на папері.
Кроки
Частина1З 4:
Загальна інформація
Частина1З 4:
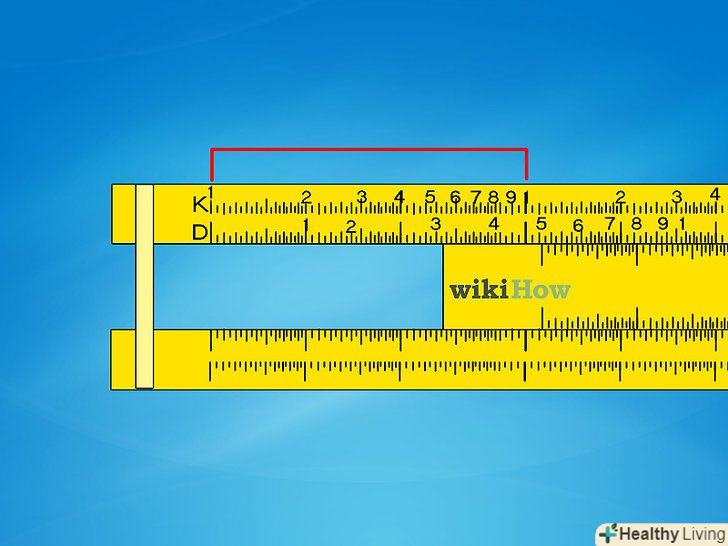
 Зверніть увагу на проміжки між цифрами.на відміну від звичайної лінійки, відстань між ними не однакове. Навпаки, воно визначається за особливою "логарифмічної" формулою, менше з одного боку і більше з іншого. Завдяки цьому ви можете поєднати дві шкали потрібним чином і отримати відповідь на завдання по множенню, як описано нижче.
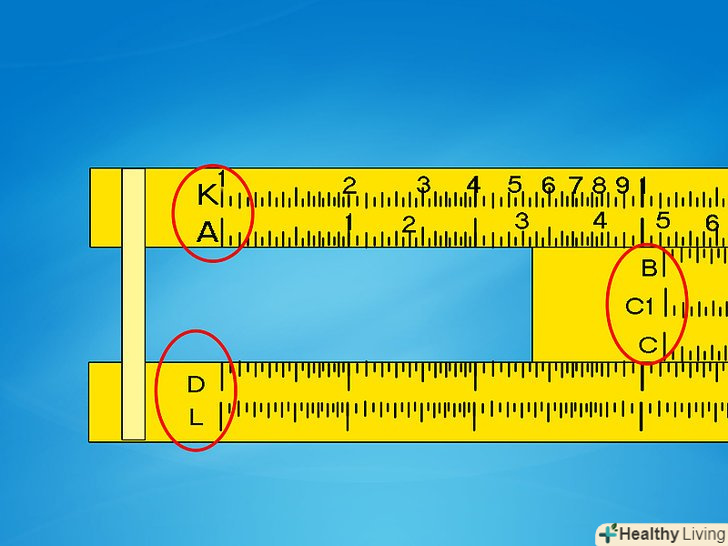
Зверніть увагу на проміжки між цифрами.на відміну від звичайної лінійки, відстань між ними не однакове. Навпаки, воно визначається за особливою "логарифмічної" формулою, менше з одного боку і більше з іншого. Завдяки цьому ви можете поєднати дві шкали потрібним чином і отримати відповідь на завдання по множенню, як описано нижче. Мітки на шкалі. кожна шкала логарифмічної лінійки має буквене або символьне позначення з лівого або правого боку. Нижче описані загальноприйняті позначення на логарифмічних лінійках:[1]
Мітки на шкалі. кожна шкала логарифмічної лінійки має буквене або символьне позначення з лівого або правого боку. Нижче описані загальноприйняті позначення на логарифмічних лінійках:[1]- Шкали C і D схожі на однорозрядну витягнуту лінійку, мітки на якій розташовані зліва направо. Така шкала називається "однорозрядної десяткової" шкалою.
- Шкали A і B «» дворазрядні десяткові " шкали. Кожна складається з двох невеликих витягнутих лінійок, розташованих впритул.
- K - це трирозрядна десяткова шкала або три витягнуті лінійки, розташовані впритул. Така шкала є не на всіх логарифмічних лінійках.
- Шкали C / і D / аналогічні C і D, але читаються справа наліво. Часто вони мають червоне забарвлення. Вони присутні не на всіх логарифмічних лінійках.
- Логарифмічні лінійки бувають різні, тому і позначення шкал може бути іншим. На деяких лінійках шкали для множення можуть бути позначені як A і B і перебувати зверху. Незалежно від буквених позначень, на багатьох лінійках поруч зі шкалами є символ π, зазначений у відповідному місці; в більшості своїй шкали знаходяться навпроти один одного, або в верхньому, або в нижньому проміжку. Рекомендуємо вирішити кілька простих завдань на множення, щоб ви могли зрозуміти, чи правильно ви використовуєте шкали. Якщо добуток 2 і 4 Не дорівнює 8, спробуйте використовувати шкали на іншій стороні лінійки.
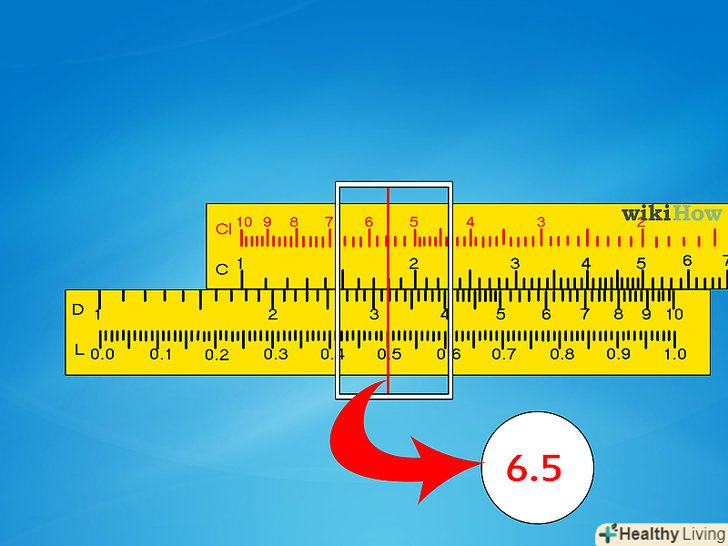
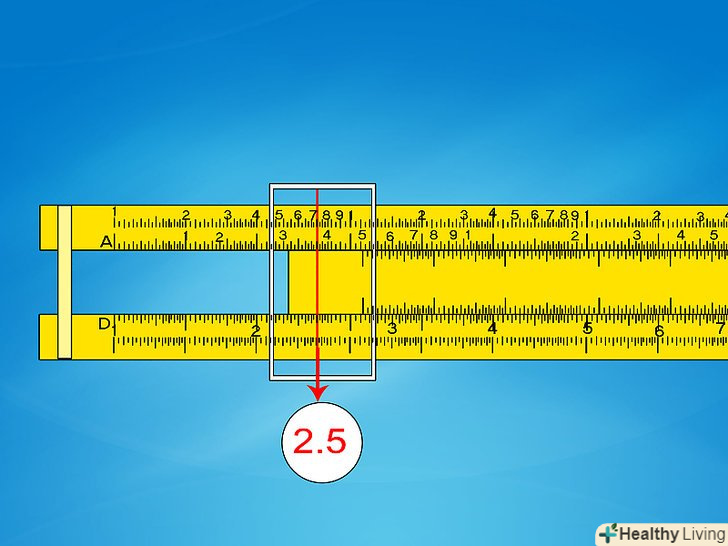
 Навчіться розуміти ділення шкали. Подивіться на вертикальні лінії на шкалі C або D і ознайомтеся з тим, як вони читаються:
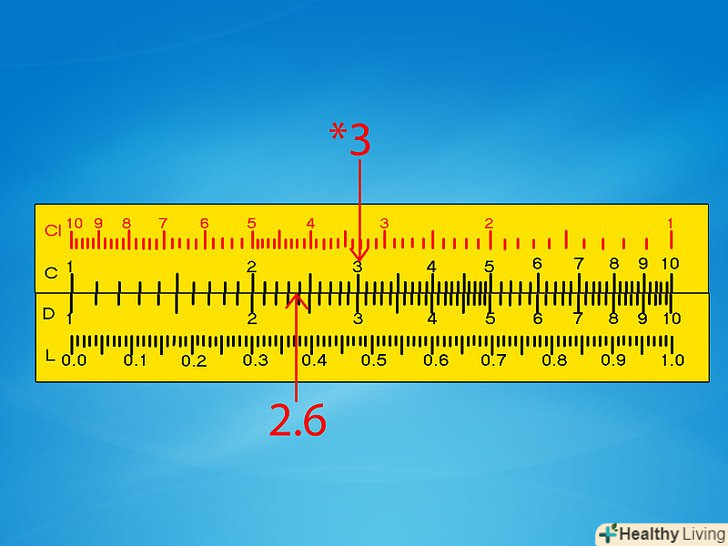
Навчіться розуміти ділення шкали. Подивіться на вертикальні лінії на шкалі C або D і ознайомтеся з тим, як вони читаються:- Основні цифри на шкалі починаються з 1 від лівого краю і тривають до 9, а потім завершуються ще однією 1 справа. Зазвичай всі вони нанесені на лінійку.
- Вторинні ділення, позначені трохи меншими вертикальними лініями, поділяють кожну основну цифру на 0,1. Вас не повинно збивати з пантелику, якщо вони позначені як «1, 2, 3«; все одно вони відповідають» 1,1; 1,2; 1,3 " і так далі.
- Також можуть бути присутніми менші поділки, які зазвичай відповідають кроку 0,02. Слідкуйте за ними уважно, так як вони можуть зникати у верхній частині шкали, де цифри знаходяться ближче один до одного.
 Не очікуйте отримати точні відповіді. при читанні шкали вам часто доведеться приходити до» найбільш ймовірного припущення", коли відповідь не буде потрапляти тютелька в тютельку. Логарифмічна лінійка використовується для швидких підрахунків, а не для максимальної точності.
Не очікуйте отримати точні відповіді. при читанні шкали вам часто доведеться приходити до» найбільш ймовірного припущення", коли відповідь не буде потрапляти тютелька в тютельку. Логарифмічна лінійка використовується для швидких підрахунків, а не для максимальної точності.- Наприклад, якщо відповідь знаходиться між відмітками 6,51 і 6,52, запишіть те значення, яке вам здається ближче. Якщо зовсім незрозуміло, то запишіть відповідь як 6,515.
Частина2З 4:
Множення
Частина2З 4:
 Запишіть числа, які ви будете множити.запишіть числа, які підлягають множенню.
Запишіть числа, які ви будете множити.запишіть числа, які підлягають множенню.- У прикладі 1 цього розділу ми підрахуємо, скільки буде 260 x 0,3.
- У прикладі 2 ми підрахуємо, скільки буде 410 x 9. Це трохи складніше, ніж Приклад 1, тому спочатку розглянемо більш просте завдання.
 Перемістіть десяткові крапки для кожного числа.логарифмічна лінійка має цифри від 1 до 10. Перемістіть десяткову точку кожного множеного числа, щоб вони відповідали своїм значенням. Після вирішення завдання ми перемістимо десяткову крапку у відповіді в потрібне положення, що буде описано в кінці розділу.
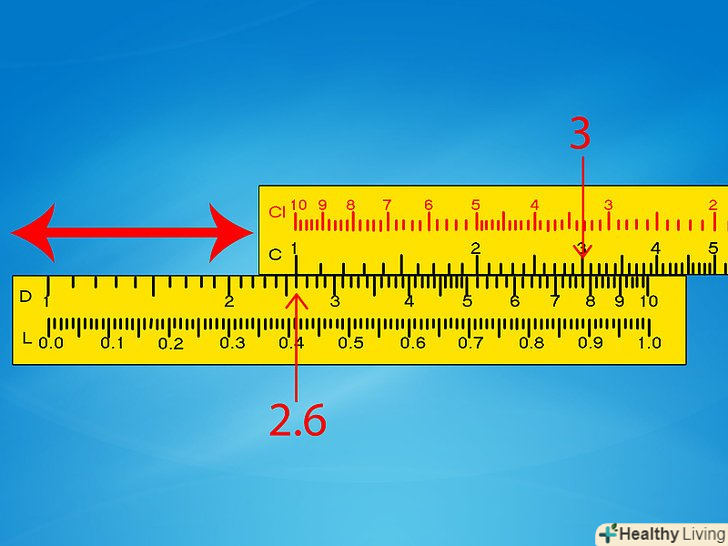
Перемістіть десяткові крапки для кожного числа.логарифмічна лінійка має цифри від 1 до 10. Перемістіть десяткову точку кожного множеного числа, щоб вони відповідали своїм значенням. Після вирішення завдання ми перемістимо десяткову крапку у відповіді в потрібне положення, що буде описано в кінці розділу.- Приклад 1: щоб підрахувати 260 x 0.3, починайте замість цього з 2,6 x 3.
- Приклад 2: щоб підрахувати 410 x 9, починайте замість цього з 4,1 x 9.
 Знайдіть менші цифри на шкалі D, потім пересуньте до неї шкалу C. знайдіть меншу цифру на шкалі D. посуньте шкалу C таким чином, щоб «1» зліва (лівий Індекс) розташовувалася на одній лінії з цією цифрою.
Знайдіть менші цифри на шкалі D, потім пересуньте до неї шкалу C. знайдіть меншу цифру на шкалі D. посуньте шкалу C таким чином, щоб «1» зліва (лівий Індекс) розташовувалася на одній лінії з цією цифрою.- Приклад 1: посуньте шкалу C таким чином, щоб лівий Індекс збігся з 2,6 на шкалі D.
- Приклад 2: посуньте шкалу C таким чином, щоб лівий Індекс збігся з 4,1 на шкалі D.
 Перемістіть металевий покажчик до другої цифри на шкалі C. Покажчик-це металевий предмет, який переміщається по всій лінійці. Зіставте покажчик з другою цифрою вашого завдання на шкалі C. Покажчик буде вказувати відповідь до задачі на шкалі D. Якщо він не переміщається так далеко, переходите до наступного кроку.
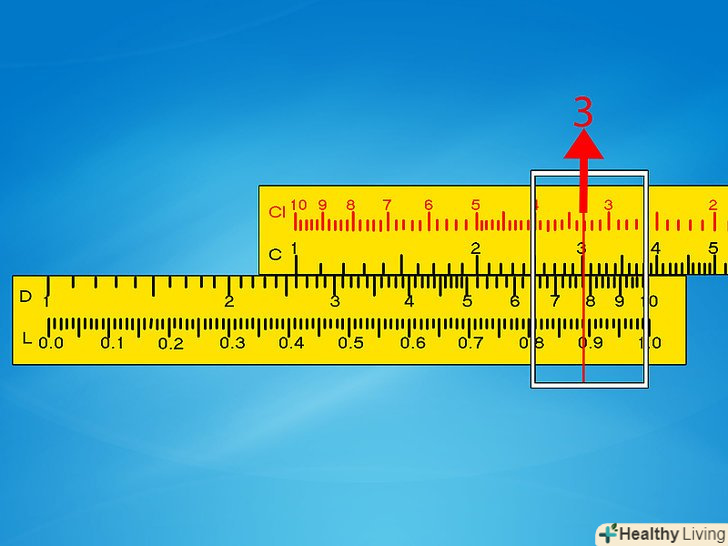
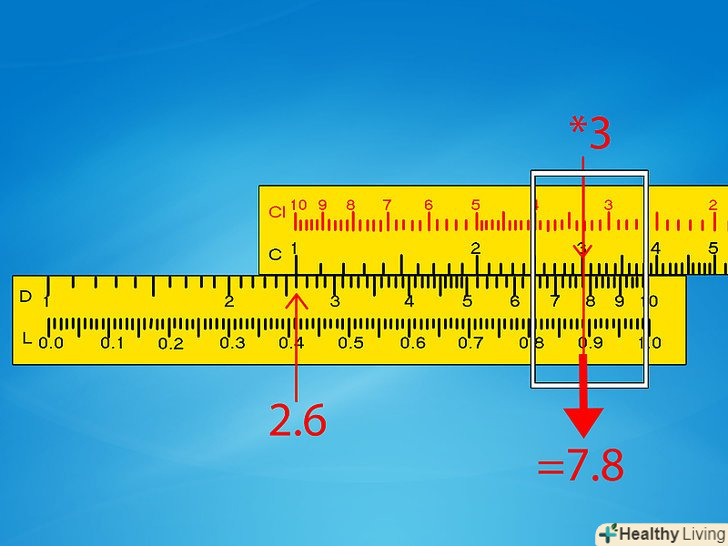
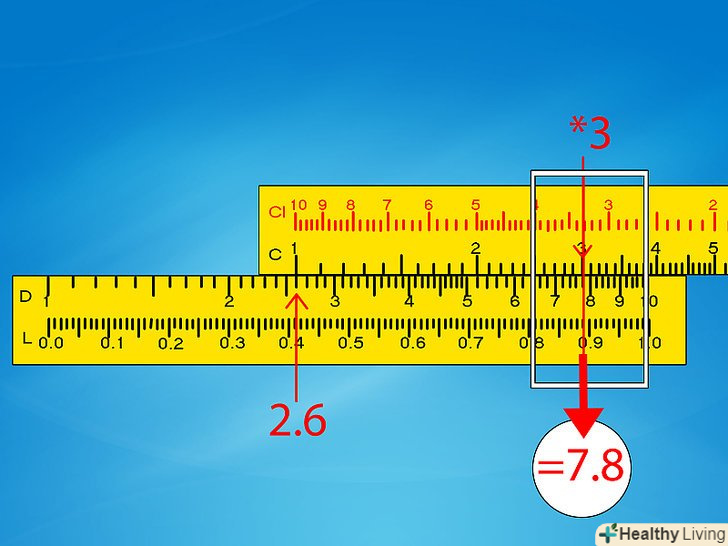
Перемістіть металевий покажчик до другої цифри на шкалі C. Покажчик-це металевий предмет, який переміщається по всій лінійці. Зіставте покажчик з другою цифрою вашого завдання на шкалі C. Покажчик буде вказувати відповідь до задачі на шкалі D. Якщо він не переміщається так далеко, переходите до наступного кроку.- Приклад 1: перемістіть покажчик до цифри 3 на шкалі C. У цьому положенні він також буде вказувати на 7,8 на шкалі D або близько того. Переходьте докроку 6.
- Приклад 2: постарайтеся перемістити покажчик так, щоб він вказував на 9 на шкалі C. Це буде неможливо на більшості лінійок або покажчик буде вказувати на порожнє місце в кінці шкали D. рішення проблеми описано в наступному кроці.
 Якщо вказівник не переміщається до відповіді, використовуйте правий Індекс.якщо покажчик блокується перегородкою в центрі лінійки або відповідь розташована за межами шкали, то використовуйте трохи інший підхід.[2] посуньте шкалу C таким чином, щоб правий Індекс або 1 праворуч розташовувалися над великим коефіцієнтом вашого завдання. Перемістіть покажчик до іншого коефіцієнта за шкалою C і прочитайте відповідь на шкалі D.
Якщо вказівник не переміщається до відповіді, використовуйте правий Індекс.якщо покажчик блокується перегородкою в центрі лінійки або відповідь розташована за межами шкали, то використовуйте трохи інший підхід.[2] посуньте шкалу C таким чином, щоб правий Індекс або 1 праворуч розташовувалися над великим коефіцієнтом вашого завдання. Перемістіть покажчик до іншого коефіцієнта за шкалою C і прочитайте відповідь на шкалі D.- Приклад 2: перемістіть шкалу C таким чином, щоб 1 справа збіглася з 9 за шкалою D. перемістіть покажчик до 4,1 за шкалою C. Покажчик показує на шкалу D в точці між 3,68 і 3,7, тому найбільш ймовірна відповідь буде 3,69.
 Прикидайте правильну десяткову крапку.незалежно від виробленого множення, ваша відповідь завжди буде зчитуватися за шкалою D, яка містить лише цифри від одного до десяти. Вам не обійтися без припущення і розумового підрахунку, щоб визначити місцезнаходження десяткової точки у фактичній відповіді.
Прикидайте правильну десяткову крапку.незалежно від виробленого множення, ваша відповідь завжди буде зчитуватися за шкалою D, яка містить лише цифри від одного до десяти. Вам не обійтися без припущення і розумового підрахунку, щоб визначити місцезнаходження десяткової точки у фактичній відповіді.- Приклад 1: нашим початковим завданням було 260 x 0,3, а лінійка дала відповідь 7,8. Округліть початкову задачу до зручних чисел і вирішіть її в голові: 250 x 0,5 = 125. Така відповідь набагато ближче до 78, ніж до 780 або 7,8, тому правильна відповідь буде78.
- Приклад 2: нашим початковим завданням було 410 x 9, а лінійка дала відповідь 3,69. Прикиньте початкову задачу як 400 x 10 = 4000. Найближчим числом буде3690, яке і стане фактичною відповіддю.
Частина3З 4:
Зведення в квадрат і куб
Частина3З 4:
 Зведення в квадрат за шкалами D і A. ці дві шкали зазвичай нерухомі. Просто перемістіть металевий покажчик до значення за шкалою D, а значення за шкалою A буде відповідати другому ступеню числа.[3] як і у випадку з множенням, положення десяткової точки доведеться визначати самостійно.
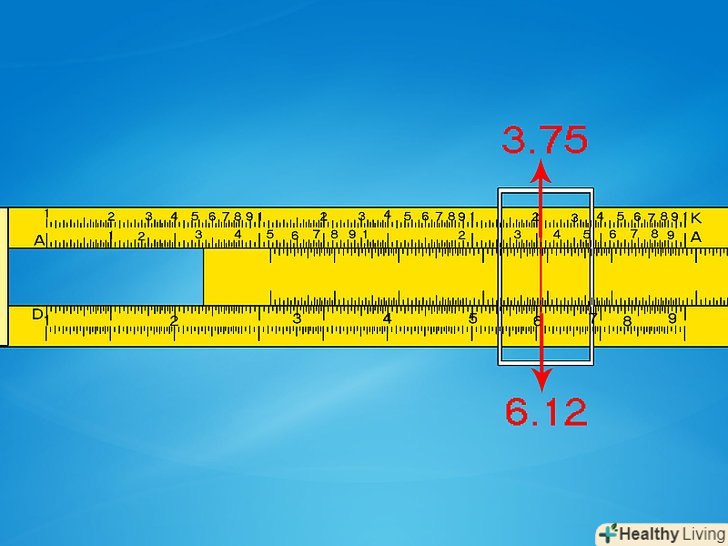
Зведення в квадрат за шкалами D і A. ці дві шкали зазвичай нерухомі. Просто перемістіть металевий покажчик до значення за шкалою D, а значення за шкалою A буде відповідати другому ступеню числа.[3] як і у випадку з множенням, положення десяткової точки доведеться визначати самостійно.- Наприклад, щоб вирішити 6,12, перемістіть покажчик до 6,1 за шкалою D. відповідне значення за шкалою A буде 3,75.
- Прикиньте 6,12 як 6 x 6 = 36. Розташуйте десяткову крапку так, щоб отримати відповідь, яка приблизно відповідає даному значенню: 37,5.
- Зверніть увагу, що точна відповідь буде 37,21. Відповідь на лінійці дає похибка в 1 %, чого цілком достатньо для практичних завдань.
 Зведення в куб за шкалами D і K. тільки що ми побачили як шкала A, яка відповідає шкалі D, зменшеній на 1/2, дозволяє звести число в квадрат. Аналогічним чином шкала K, яка відповідає шкалі D, зменшеній на 1/3, дозволяє звести число в куб. Просто перемістіть покажчик до значення за шкалою D і прочитайте результат на шкалі K. Прикиньте розташування десяткової точки.
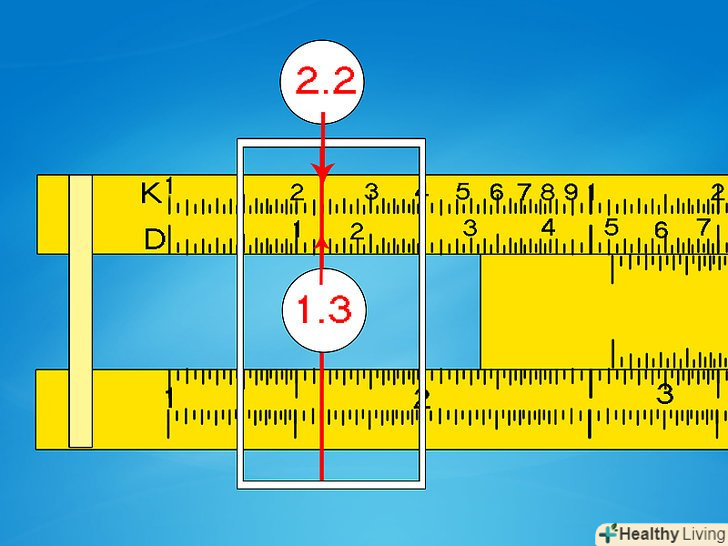
Зведення в куб за шкалами D і K. тільки що ми побачили як шкала A, яка відповідає шкалі D, зменшеній на 1/2, дозволяє звести число в квадрат. Аналогічним чином шкала K, яка відповідає шкалі D, зменшеній на 1/3, дозволяє звести число в куб. Просто перемістіть покажчик до значення за шкалою D і прочитайте результат на шкалі K. Прикиньте розташування десяткової точки.- Наприклад, щоб вирішити 1303, перемістіть покажчик до 1,3 за шкалою D. відповідне значення за шкалою K буде 2,2. Так як 1003 = 1 x 106, і 2003 = 8 x 106, ми розуміємо, що відповідь буде десь посередині. Відповідь повинна бути 2,2 x 106, або 2 200 000.
Частина4З 4:
Витяг квадратного і кубічного кореня
Частина4З 4:
 Запишіть число в експоненціальному поданні для вилучення квадратного кореня. як і завжди, на лінійці є тільки значення від 1 до 10, тому для вилучення квадратного кореня вам буде потрібно записати число в експоненціальному поданні.
Запишіть число в експоненціальному поданні для вилучення квадратного кореня. як і завжди, на лінійці є тільки значення від 1 до 10, тому для вилучення квадратного кореня вам буде потрібно записати число в експоненціальному поданні.- Приклад 3: для вирішення √(390) запишіть завдання як √(3,9 x 102).
- Приклад 4: для вирішення √(7100) запишіть завдання як √(7,1 x 103).
 Визначте, яку сторону шкали a необхідно використовувати. щоб витягти квадратний корінь числа, для початку перемістіть покажчик до цього числа за шкалою A. але так як шкала A нанесена двічі, необхідно вирішити, яку використовувати.[4] у цьому допоможуть наступні правила:
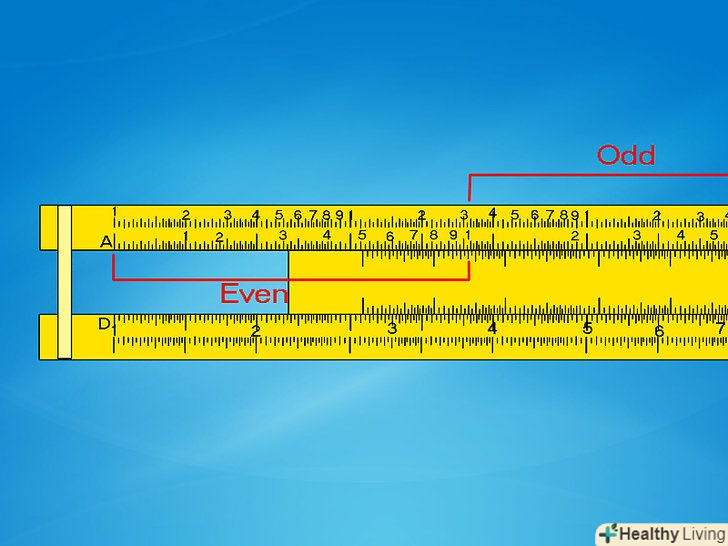
Визначте, яку сторону шкали a необхідно використовувати. щоб витягти квадратний корінь числа, для початку перемістіть покажчик до цього числа за шкалою A. але так як шкала A нанесена двічі, необхідно вирішити, яку використовувати.[4] у цьому допоможуть наступні правила:- Якщо експонента вашого числа парна (як2 в прикладі 3), Використовуйте ліву сторону шкали A («перший десятковий розряд»).
- Якщо експонента вашого числа непарна (як3 в прикладі 4), використовуйте праву сторону шкали A («другий десятковий розряд»).
 Перемістіть покажчик за шкалою A. поки опустіть експоненту десяти і перемістіть металевий покажчик за шкалою A до необхідного значення.
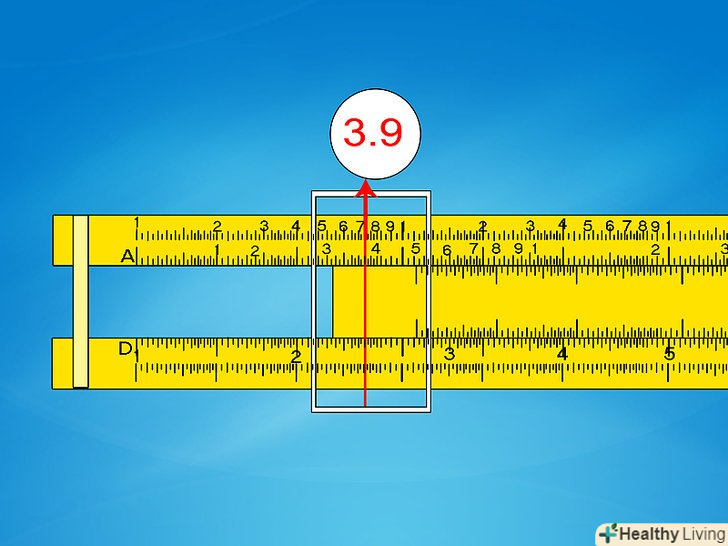
Перемістіть покажчик за шкалою A. поки опустіть експоненту десяти і перемістіть металевий покажчик за шкалою A до необхідного значення.- Приклад 3: для вирішення √(3,9 x 102) перемістіть покажчик до 3,9 зліва за шкалою A (використовуємо ліву шкалу, так як експонента парна).
- Приклад 4: для вирішення √(7,1 x 103) перемістіть покажчик до 7,1 праворуч за шкалою A (використовуємо праву шкалу, так як експонента непарна).
 Знаходимо відповідь за шкалою D. Прочитайте значення за шкалою D, на яке наведений Покажчик. Додайте до нього " x10n". Для підрахунку N візьміть вихідну ступінь 10, округліть в меншу сторону до найближчого парного числа і розділіть на 2.
Знаходимо відповідь за шкалою D. Прочитайте значення за шкалою D, на яке наведений Покажчик. Додайте до нього " x10n". Для підрахунку N візьміть вихідну ступінь 10, округліть в меншу сторону до найближчого парного числа і розділіть на 2.- Приклад 3: відповідне значення шкали D при A=3,9 буде 1,975. Початкова цифра в експоненціальному поданні мала 102. 2 вже парна, тому просто розділіть на 2, щоб отримати 1. Остаточна відповідь буде 1,975 x 101 = 19,75.
- Приклад 4: відповідне значення шкали D при A=7,1 буде 8,45. Початкова цифра в експоненціальному поданні мала 103, тому округлите 3 до найближчого парного числа, 2, а потім розділіть на 2, щоб отримати 1. Остаточна відповідь буде 8,45 x 101 = 84,5.
 Аналогічним способом витягуйте кубічні корені за шкалою K. процес вилучення кубічного кореня дуже схожий. Найголовніше-визначити, яку з трьох шкал k слід використовувати. Для цього розділіть кількість цифр вашого числа на три і дізнайтеся залишок. Якщо залишок 1, Використовуйте першу шкалу. Якщо 2, Використовуйте другу шкалу. Якщо 3, Використовуйте третю шкалу (ще один спосіб — багаторазово рахувати від першої шкали до третьої, поки не досягнете кількості цифр у вашій відповіді).[5]
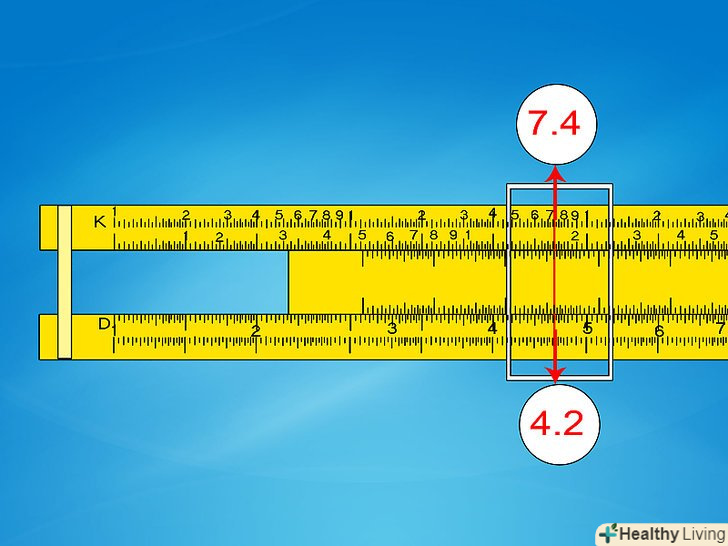
Аналогічним способом витягуйте кубічні корені за шкалою K. процес вилучення кубічного кореня дуже схожий. Найголовніше-визначити, яку з трьох шкал k слід використовувати. Для цього розділіть кількість цифр вашого числа на три і дізнайтеся залишок. Якщо залишок 1, Використовуйте першу шкалу. Якщо 2, Використовуйте другу шкалу. Якщо 3, Використовуйте третю шкалу (ще один спосіб — багаторазово рахувати від першої шкали до третьої, поки не досягнете кількості цифр у вашій відповіді).[5]- Приклад 5: для вилучення кубічного кореня з 74 000 необхідно підрахувати кількість цифр (5), розділити його на 3 і дізнатися залишок (1, залишок 2). Так як залишок 2, використовуємо другу шкалу (також можна виконати рахунок за шкалами п'ять разів: 1-2-3-1–2).
- Перемістіть курсор до 7,4 за другою шкалою K. відповідне значення за шкалою D буде приблизно 4,2.
- Так як 103 менше 74 000, але 1003 більше 74 000, відповідь повинна бути в рамках від 10 до 100. Перемістіть десяткову крапку, щоб отримати 42.
Поради
- Логарифмічна лінійка дозволяє також виконувати розрахунок інших функцій, особливо якщо на ній є шкала логарифмів, шкала тригонометричних розрахунків або інші спеціалізовані шкали. Спробуйте розібратися в них самостійно або почитайте інформацію в Інтернеті.
- Можна використовувати метод множення для перетворення між двома одиницями виміру. Наприклад, оскільки 1 дюйм = 2,54 сантиметра, завдання «перетворити 5 дюймів в сантиметри» можна трактувати як приклад множення 5 x 2,54.
- Точність логарифмічної лінійки залежить від кількості помітних масштабних відміток. Чим більше довжина лінійки, тим вище її точність.
Попередження
- Не допускайте впливу на логарифмічну лінійку тепла і вологи. Викривлення і всихання конструкції призведе до зниження точності лінійки.[6]
Джерела
- ↑ Http://sliderulemuseum.com/SR_Course.htm
- ↑ Http://sliderulemuseum.com/SR_Course.htm
- ↑ Http://www.sliderules.info/a-to-z/tys/tys03.htm# A%20and%20B%20Scales
- ↑ Http://www.sliderules.info/a-to-z/tys/tys03.htm# A%20and%20B%20Scales
- ↑ Http://www.antiquark.com/sliderule/sim/sr-calcs-by-example.html# mozTocId734623
- ↑ Http://www.sliderules.info/a-to-z/tys/tys03.htm