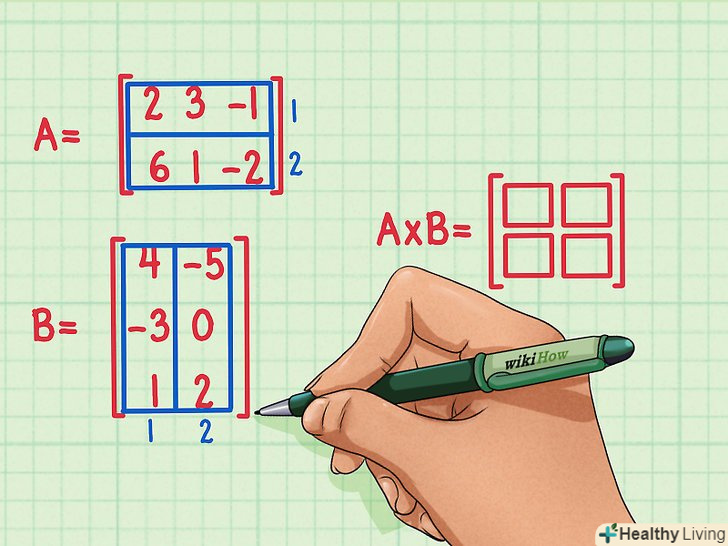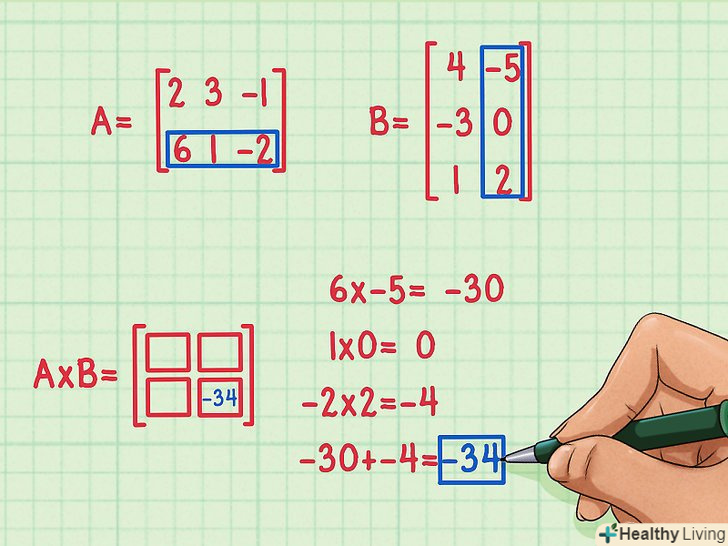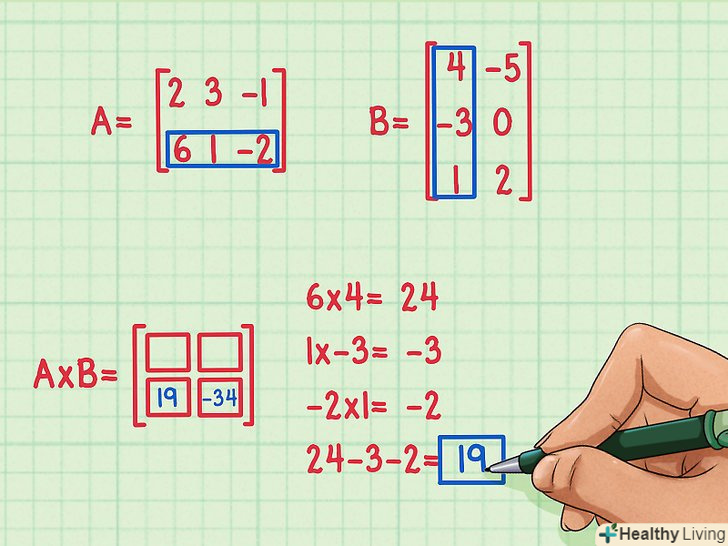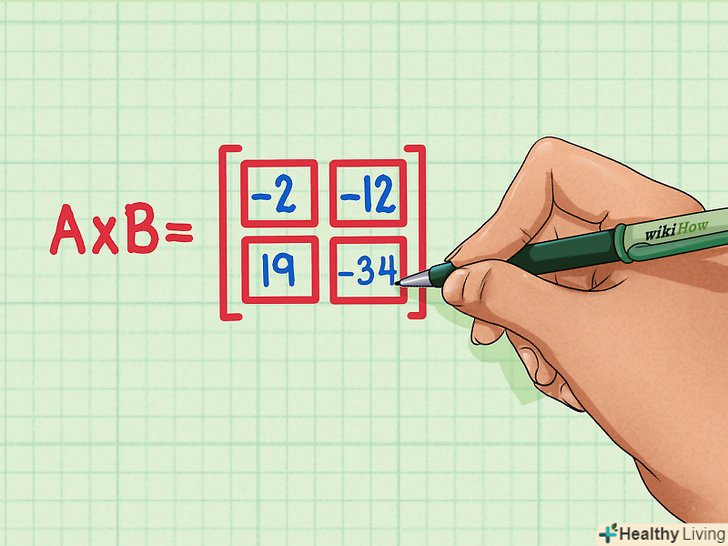Матриця являє собою прямокутне розташування чисел, символів або виразів в рядках і стовпцях. Щоб помножити матриці, вам потрібно помножити елементи (або числа) в рядках першої матриці на елементи в стовпцях другої матриці і скласти отримані значення. Для множення матриць потрібно множення, додавання і правильна розстановка результатів.
Кроки
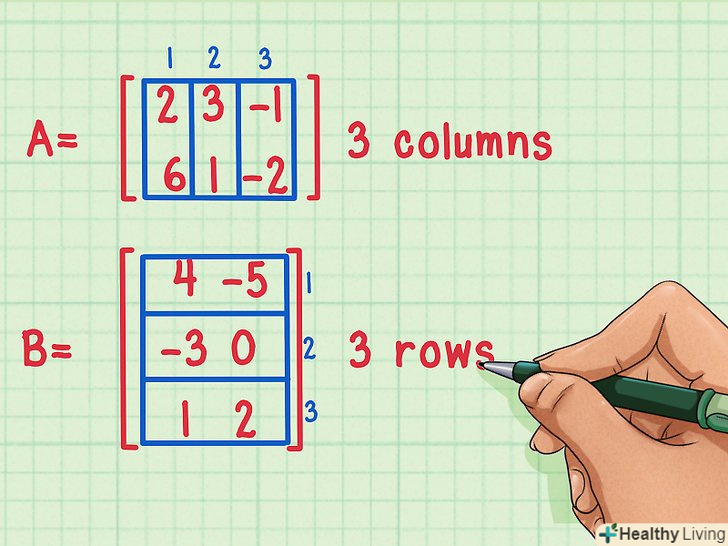
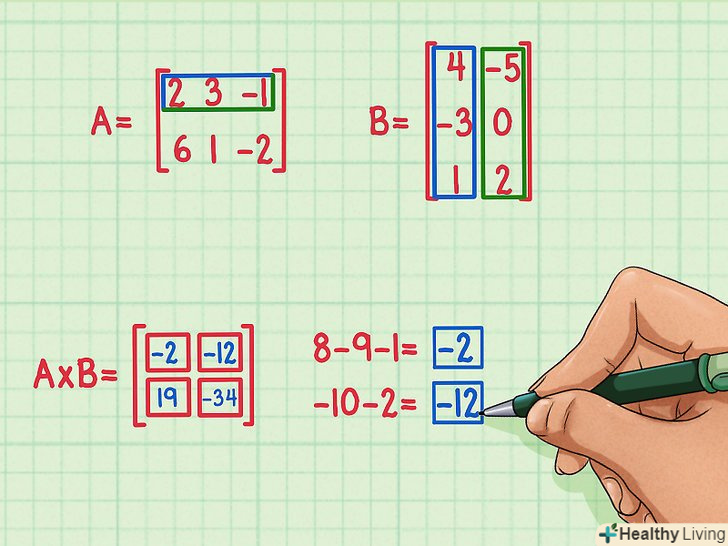
Множення матриць.у даній статті розглядається множення матриць рівних розмірів, тобто таких, у яких число рядків першої матриці дорівнює числу рядків другої матриці.- На малюнку: перша матриця А має два рядки, а друга матриця B має два стовпці.
-
Позначте розміри кінцевої матриці. намалюйте нову порожню матрицю, яка буде кінцевою матрицею-результатом добутку першої матриці на другу. Кінцева матриця має стільки ж рядків, як матриця А, і стільки ж стовпців, як матриця в.
- Матриця А має 2 рядки, тому кінцева матриця матиме 2 рядки.
- Матриця B має 2 стовпці, тому кінцева матриця матиме 2 стовпці.
- Кінцева матриця матиме 2 рядки і 2 стовпці.
-
Знайдіть перший скалярний твір. для цього помножте перший елемент першого рядка на перший елемент першого стовпця, другий елемент першого рядка на другий елемент першого стовпця, третій елемент першого рядка на третій елемент першого стовпця. Потім складіть отримані значення. Наприклад, помножимо другий рядок на другий стовпець (і знайдемо четвертий скалярний добуток):
- 6 x -5 = -30
- 1 x 0 = 0
- -2 x 2 = -4
- -30 + 0 + (-4) = -34
- Четвертий скалярний добуток дорівнює (-34) і він записується в правому нижньому куті кінцевої матриці.
- Результат скалярного добутку записується згідно з номерами множиться рядка і стовпця. Наприклад, коли Ви знайшли скалярний твір другого рядка (матриця А) і другого стовпця (матриця B), результат (-34) записується на перетині другого рядка і другого стовпця кінцевої матриці.
-
Знайдіть другий скалярний твір.для цього помножте елементи другого рядка першої матриці на елементи першого стовпця другої матриці, а потім складіть результати.
- 6 x 4 = 24
- 1 x (-3) = -3
- (-2) x 1 = -2
- 24 + (-3) + (-2) = 19
- Другий скалярний добуток дорівнює (-19), і він записується на перетині другого рядка і першого стовпця кінцевої матриці.
-
Знайдіть решту скалярних творів. Перший скалярний добуток обчислюється множенням елементів першого рядка на елементи першого стовпця:
- 2 x 4 = 8
- 3 x (-3) = -9
- (-1) x 1 = -1
- 8 + (-9) + (-1) = -2
- Перший скалярний добуток дорівнює (-2), і він записується на перетині першого рядка і першого стовпця кінцевої матриці.
- Третій скалярний добуток обчислюється множенням елементів першого рядка на елементи другого стовпця:
- 2 x (-5) = -10
- 3 x 0 = 0
- (-1) x 2 = -2
- -10 + 0 + (-2) = -12
- Третій скалярний добуток дорівнює (-12), і він записується на перетині першого рядка і другого стовпця кінцевої матриці.
-
Переконайтеся, що результати всіх чотирьох скалярних творів правильно розставлені.
Поради
- Результат добутку двох матриць має стільки ж рядків, як перша матриця, і стільки ж стовпців, як друга матриця.
- Записуйте ваші обчислення. Множення матриць включає багато розрахунків, в яких легко заплутатися.
