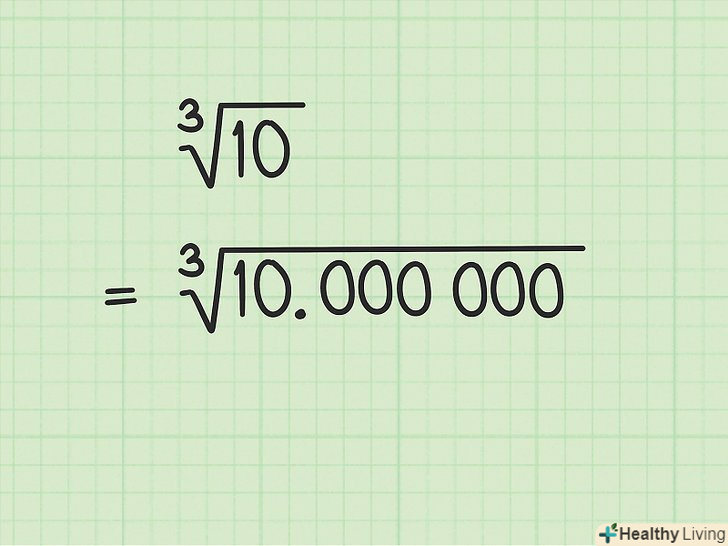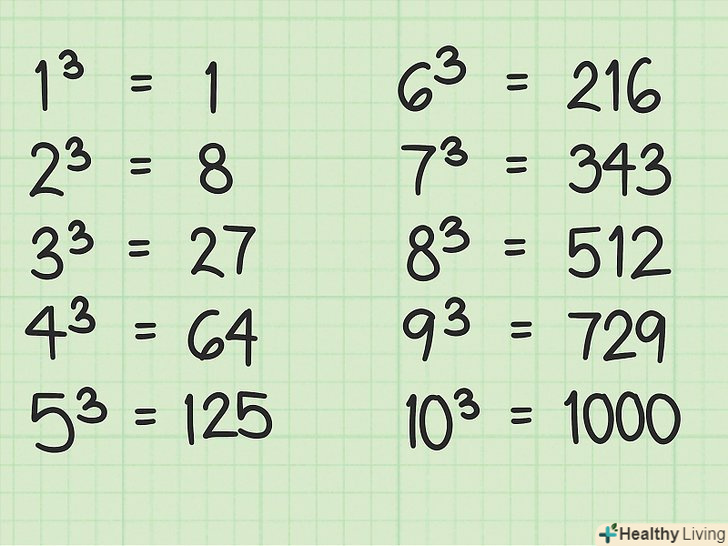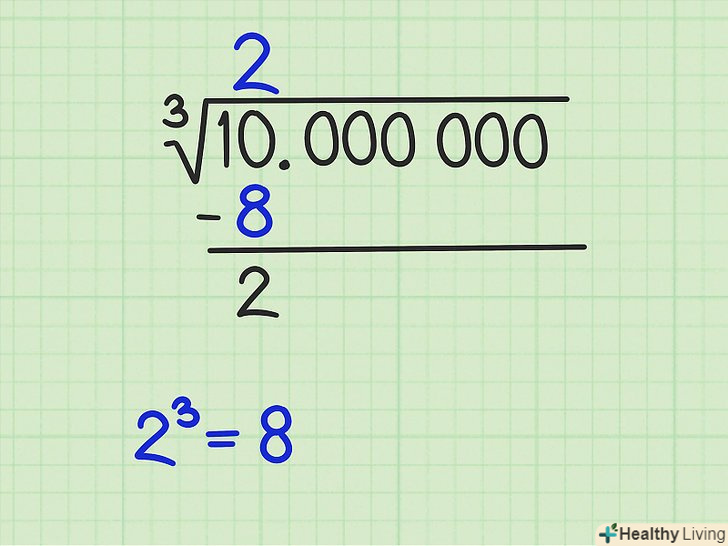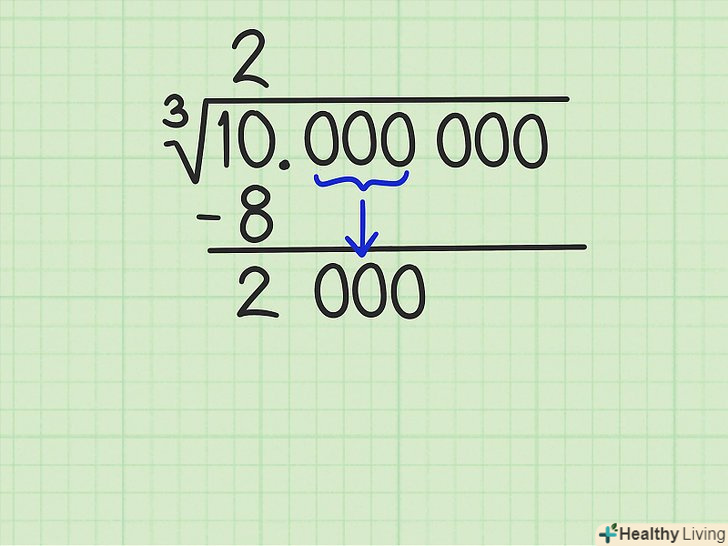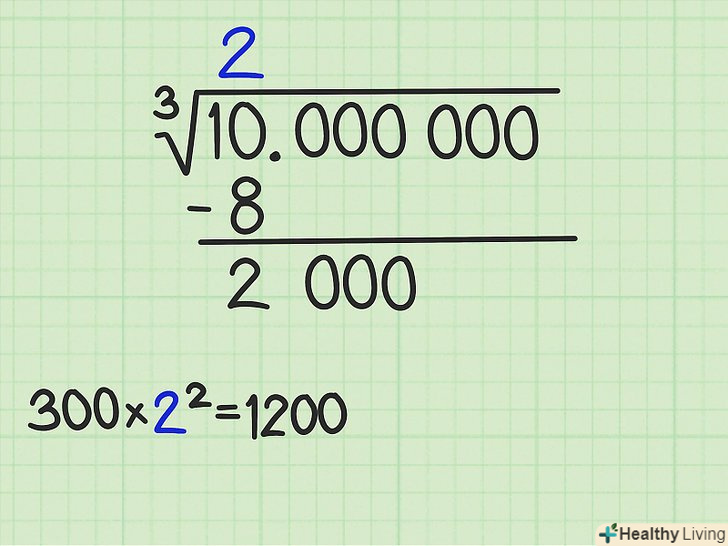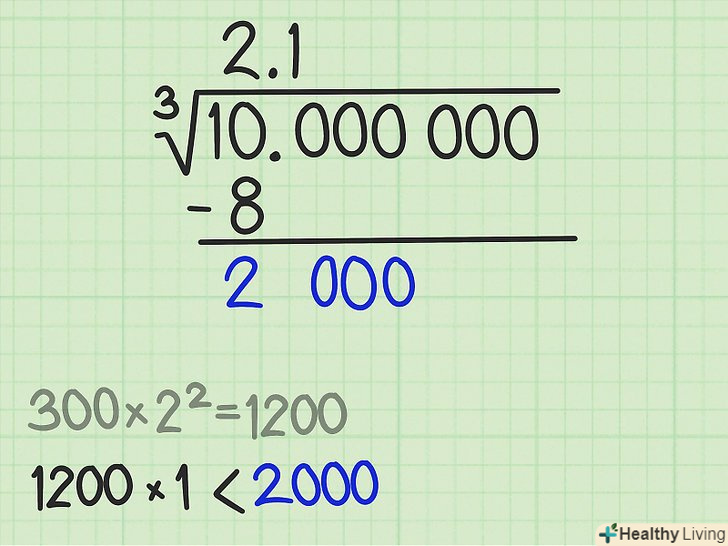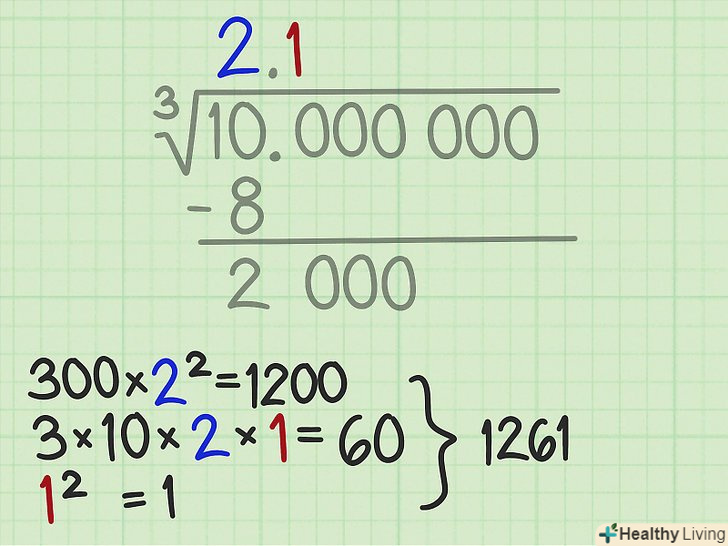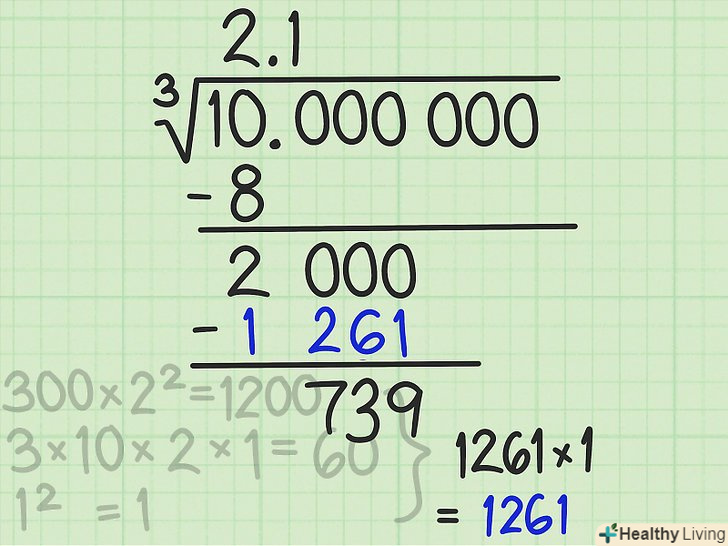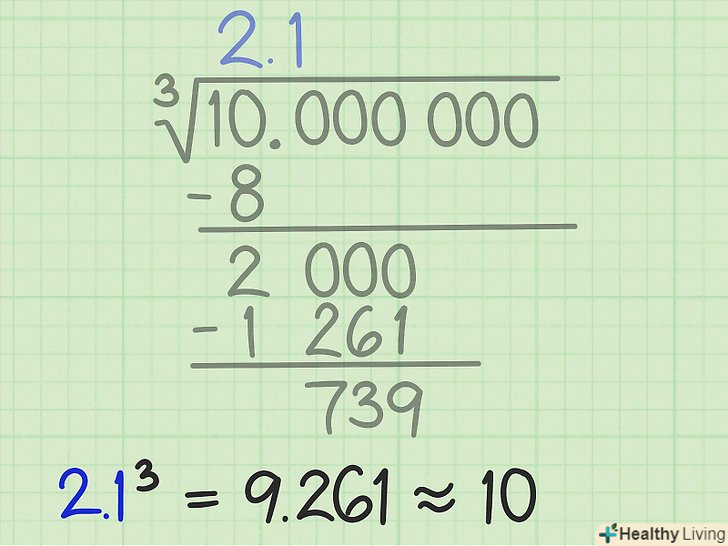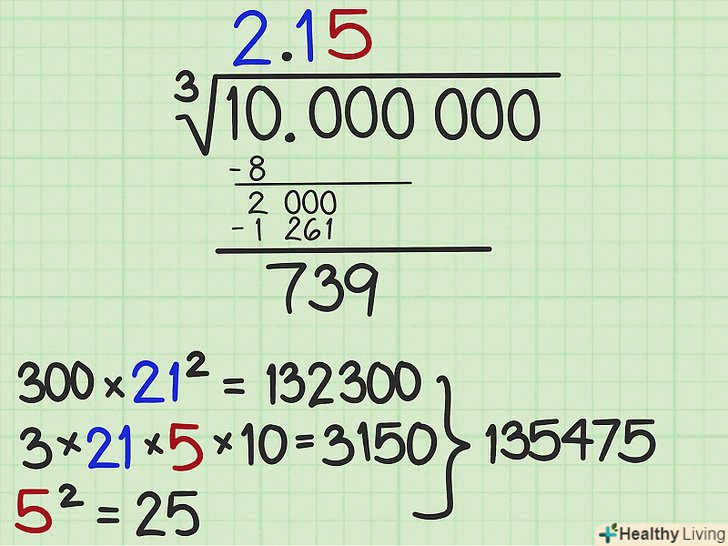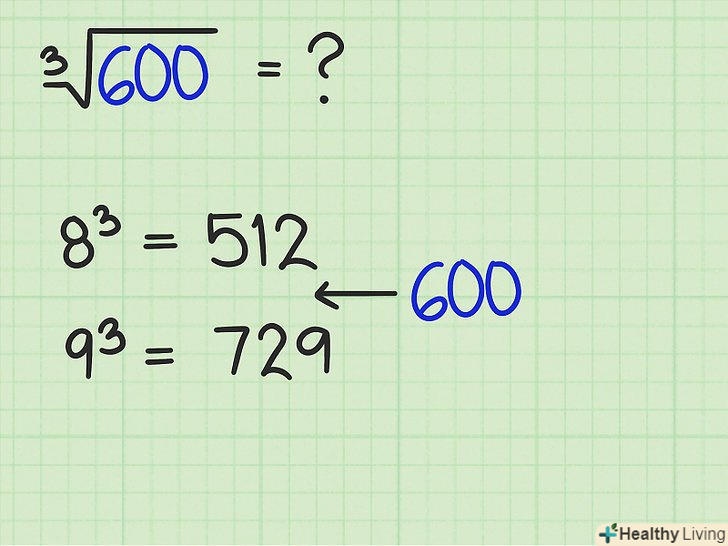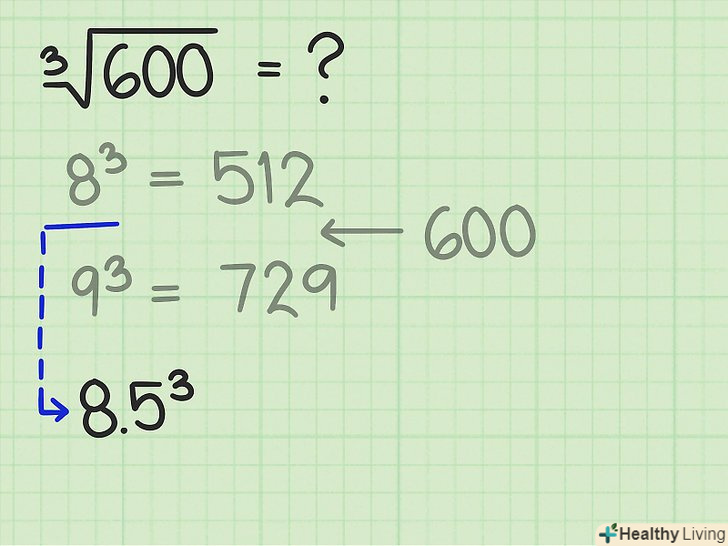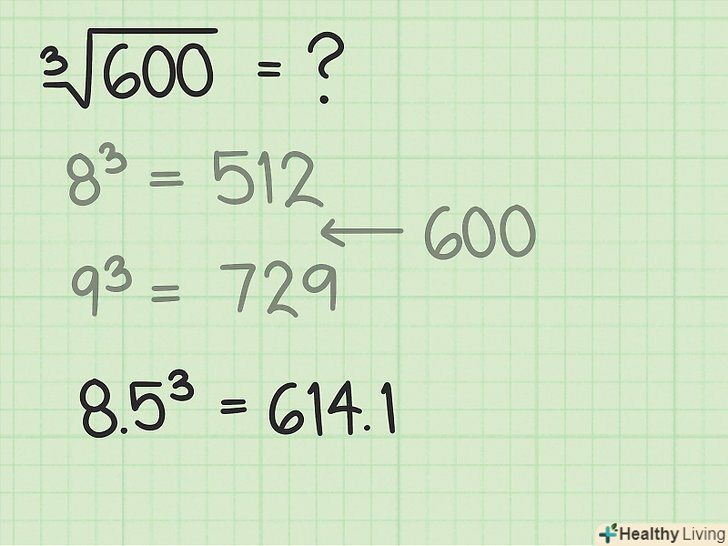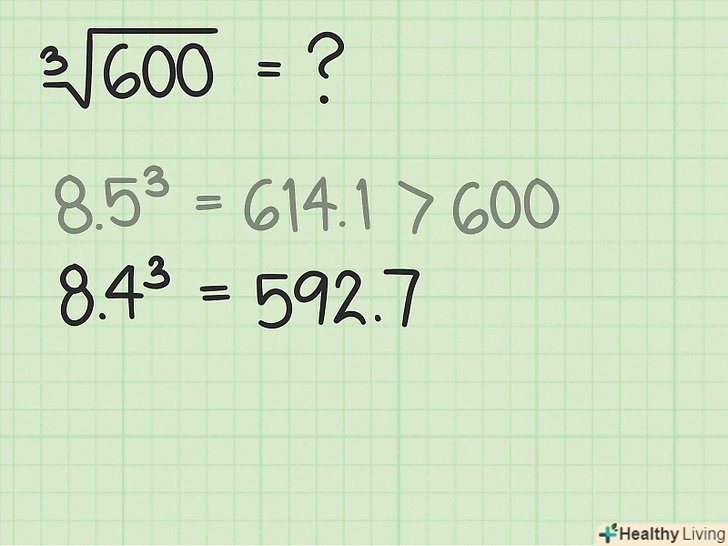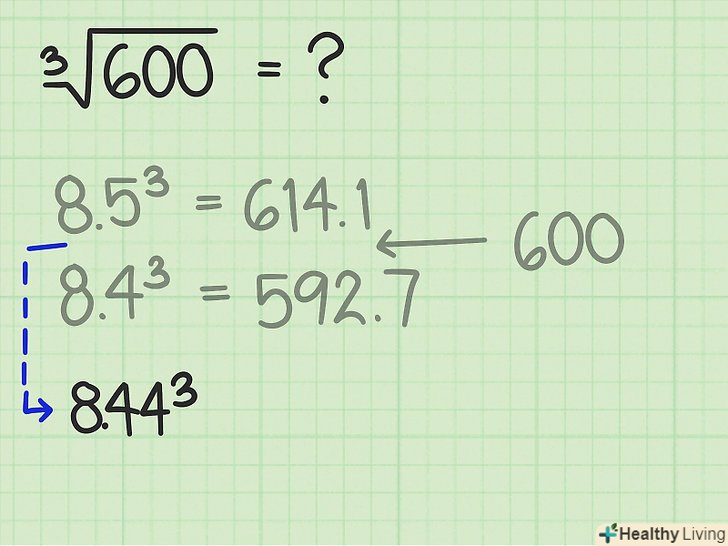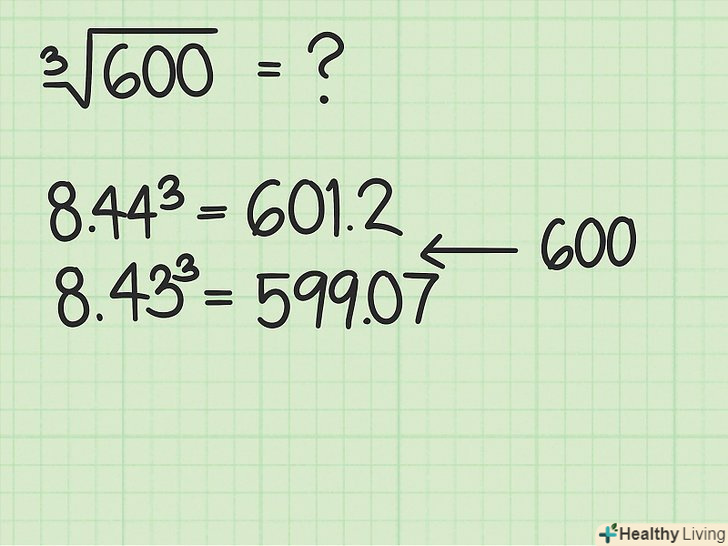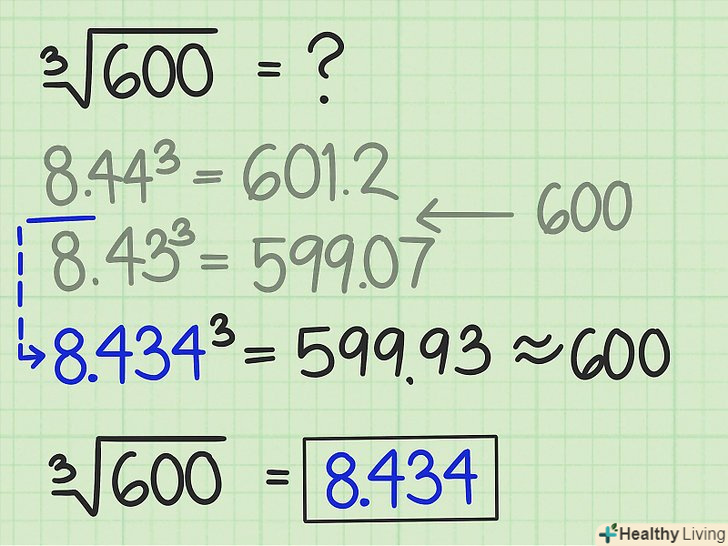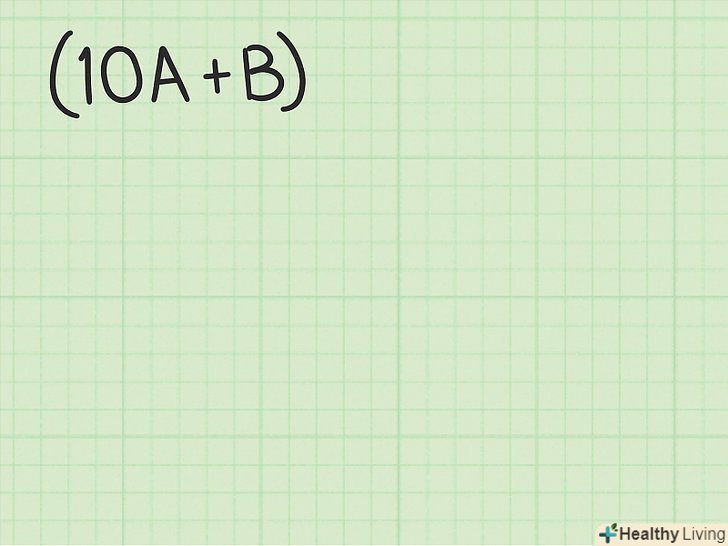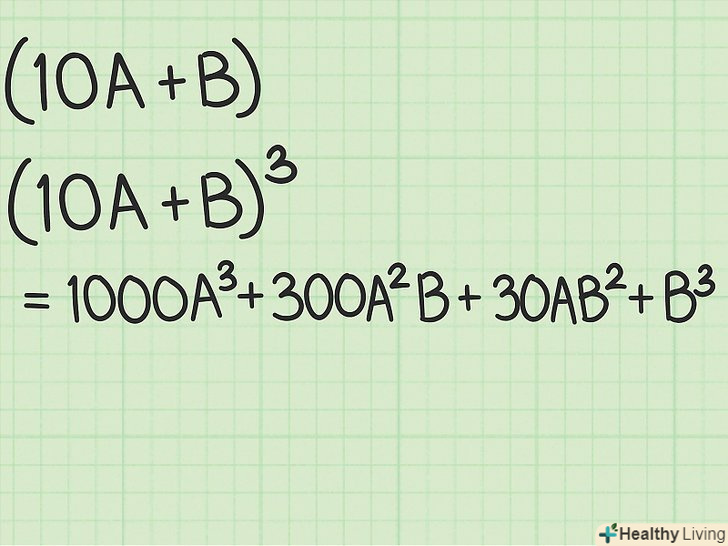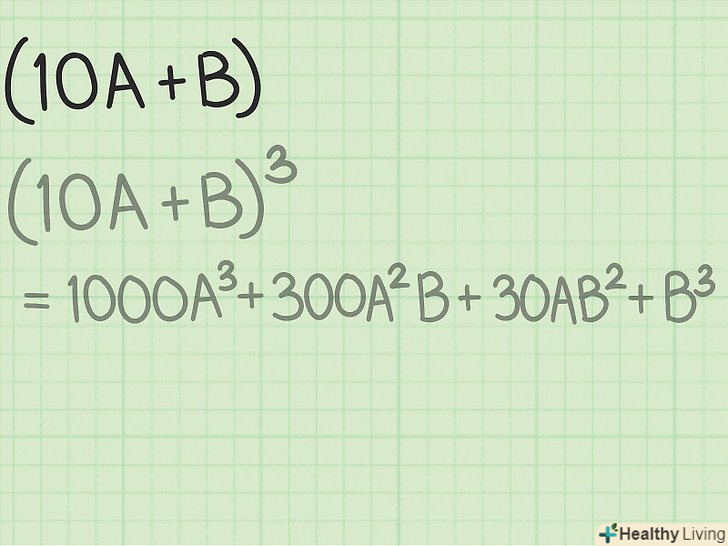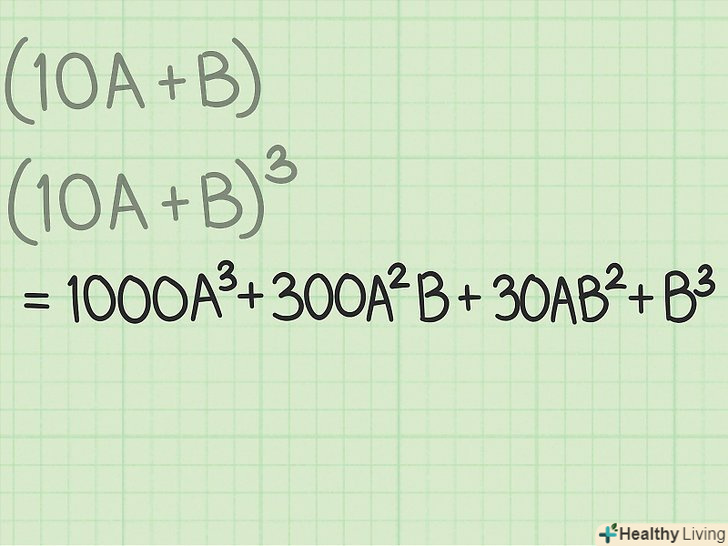Якщо під рукою є калькулятор, витягти кубічний корінь з будь-якого числа не складе ніяких проблем. Але якщо калькулятора немає або ви просто хочете справити враження на оточуючих, витягніть кубічний корінь вручну. Більшості людей описуваний тут процес здасться досить складним, але з практикою витягувати кубічні коріння стане набагато легше. Перед тим як приступити до читання даної статті, згадайте основні математичні операції та обчислення з числами в кубі.
Кроки
Частина1З 3:
Витяг кубічного кореня на простому прикладі
Частина1З 3:
 Запишіть завдання.Витяг кубічного кореня вручну схоже на поділ в стовпчик, але з деякими нюансами. Спочатку запишіть завдання в певній формі.[1]
Запишіть завдання.Витяг кубічного кореня вручну схоже на поділ в стовпчик, але з деякими нюансами. Спочатку запишіть завдання в певній формі.[1]- Запишіть число, з якого потрібно витягти кубічний корінь. Число розбийте на групи по три цифри, причому відлік почніть з десяткової коми. Наприклад, потрібно витягти кубічний корінь з 10. Напишіть це число так: 10, 000 000. Додаткові нулі покликані підвищити точність результату.
- Біля і над числом намалюйте знак кореня. Уявіть, що це горизонтальна і вертикальна лінії, які ви малюєте при розподілі в стовпчик. Єдина відмінність-це форма двох знаків.
- Над горизонтальною лінією поставте десяткову кому. Зробіть це безпосередньо над десятковою комою вихідного числа.
 Запам'ятайте результати зведення в куб цілих чисел.вони будуть використані в обчисленнях.
Запам'ятайте результати зведення в куб цілих чисел.вони будуть використані в обчисленнях. Знайдіть першу цифру відповіді. виберіть куб цілого числа, який найближче, але менше першої групи з трьох цифр.[2]
Знайдіть першу цифру відповіді. виберіть куб цілого числа, який найближче, але менше першої групи з трьох цифр.[2]- У нашому прикладі перша група з трьох цифр-це число 10. Знайдіть найбільший куб, який менше 10. Таким кубом є 8, а кубічний корінь з 8 дорівнює 2.
- Над горизонтальною лінією над цифрою 10 напишіть цифру 2. Потім запишіть значення операції
= 8 під 10. Проведіть риску і відніміть 8 з 10 (як при звичайному розподілі в стовпчик). В результаті вийде 2 (це перший залишок).
- Таким чином, Ви знайшли першу цифру відповіді. Подумайте, чи є даний результат досить точним. У більшості випадків це буде дуже приблизна відповідь. Зведіть результат в куб, щоб з'ясувати, наскільки він близький до вихідного числа. У нашому прикладі:
= 8, що не дуже близько до 10, тому обчислення треба продовжити.
 Знайдіть наступну цифру відповіді.до першого залишку припишіть другу групу з трьох цифр, а зліва від отриманого числа проведіть вертикальну риску. За допомогою отриманого числа ви знайдете другу цифру відповіді. У нашому прикладі до першого залишку (2) потрібно приписати другу групу з трьох цифр (000), щоб отримати число 2000.[3]
Знайдіть наступну цифру відповіді.до першого залишку припишіть другу групу з трьох цифр, а зліва від отриманого числа проведіть вертикальну риску. За допомогою отриманого числа ви знайдете другу цифру відповіді. У нашому прикладі до першого залишку (2) потрібно приписати другу групу з трьох цифр (000), щоб отримати число 2000.[3]- Зліва від вертикальної лінії ви напишіть три числа, сума яких дорівнює якомусь першому множнику. Залиште порожні простору для цих чисел, а між ними поставте знаки «плюс».
 Знайдіть перший доданок (з трьох).у першому порожньому просторі запишіть результат множення числа 300 на квадрат першої цифри відповіді (вона записана над знаком кореня). У нашому прикладі першою цифрою відповіді є 2, тому 300*(2^2) = 300*4 = 1200. Напишіть 1200 у першому порожньому просторі. Першим доданком є число 1200 (плюс ще два числа, які потрібно знайти).[4]
Знайдіть перший доданок (з трьох).у першому порожньому просторі запишіть результат множення числа 300 на квадрат першої цифри відповіді (вона записана над знаком кореня). У нашому прикладі першою цифрою відповіді є 2, тому 300*(2^2) = 300*4 = 1200. Напишіть 1200 у першому порожньому просторі. Першим доданком є число 1200 (плюс ще два числа, які потрібно знайти).[4] Знайдіть другу цифру відповіді.З'ясуйте, на яке число потрібно помножити 1200, щоб результат був близький, але не перевищував 2000. Таким числом може бути тільки 1, так як 2*1200 = 2400, що більше 2000. Напишіть 1 (друга цифра відповіді) після 2 і десяткової коми над знаком кореня.[5]
Знайдіть другу цифру відповіді.З'ясуйте, на яке число потрібно помножити 1200, щоб результат був близький, але не перевищував 2000. Таким числом може бути тільки 1, так як 2*1200 = 2400, що більше 2000. Напишіть 1 (друга цифра відповіді) після 2 і десяткової коми над знаком кореня.[5] Знайдіть другий і третій доданки (з трьох).множник складається з трьох чисел (доданків), перше з яких ви вже знайшли (1200). Тепер потрібно знайти залишилися два доданків.[6]
Знайдіть другий і третій доданки (з трьох).множник складається з трьох чисел (доданків), перше з яких ви вже знайшли (1200). Тепер потрібно знайти залишилися два доданків.[6]- Помножте 3 на 10 і на кожну цифру відповіді (вони записані над знаком кореня). У нашому прикладі: 3*10*2*1 = 60. Додайте цей результат до 1200 і отримаєте 1260.
- Нарешті, зведіть в квадрат останню цифру відповіді. У нашому прикладі останньою цифрою відповіді є 1, тому 1^2 = 1. Таким чином, перший множник дорівнює сумі наступних чисел: 1200 + 60 + 1 = 1261. Запишіть це число зліва від вертикальної риси.
 Помножте і відніміть.помножте останню цифру відповіді (в нашому прикладі це 1) на знайдений множник (1261): 1*1261 = 1261. Запишіть це число під 2000 і відніміть його з 2000. Ви отримаєте 739 (це другий залишок).
Помножте і відніміть.помножте останню цифру відповіді (в нашому прикладі це 1) на знайдений множник (1261): 1*1261 = 1261. Запишіть це число під 2000 і відніміть його з 2000. Ви отримаєте 739 (це другий залишок). Подумайте, чи є отримана відповідь досить точною.робіть це кожен раз, після того як завершите чергове віднімання. Після першого віднімання відповідь дорівнювала 2, що не є точним результатом. Після другого віднімання відповідь дорівнює 2,1.[7]
Подумайте, чи є отримана відповідь досить точною.робіть це кожен раз, після того як завершите чергове віднімання. Після першого віднімання відповідь дорівнювала 2, що не є точним результатом. Після другого віднімання відповідь дорівнює 2,1.[7]- Щоб перевірити точність відповіді, зведіть його в куб: 2,1*2,1*2,1 = 9,261.
- Якщо ви вважаєте, що відповідь досить точний, обчислення можна не продовжувати; в іншому випадку виконайте ще одне віднімання.
 Знайдіть другий множник. щоб попрактикуватися в обчисленнях і отримати більш точний результат, повторіть дії, які описані вище.[8]
Знайдіть другий множник. щоб попрактикуватися в обчисленнях і отримати більш точний результат, повторіть дії, які описані вище.[8]- До другого залишку (739) припишіть третю групу з трьох цифр (000). Ви отримаєте число 739000.
- Помножте 300 на квадрат числа, яке записано над знаком кореня (21):
= 132300.
- Знайдіть третю цифру відповіді. З'ясуйте, на яке число потрібно помножити 132300, щоб результат був близький, але не перевищував 739000. Таким числом є 5: 5 * 132200 = 661500. Напишіть 5 (третя цифра відповіді) після 1 над знаком кореня.
- Помножте 3 на 10 на 21 і на останню цифру відповіді (вони записані над знаком кореня). У нашому прикладі:
.
- Нарешті, зведіть в квадрат останню цифру відповіді. У нашому прикладі останньою цифрою відповіді є 5, тому
- Таким чином, другий множник дорівнює: 132300 + 3150 + 25 = 135475.
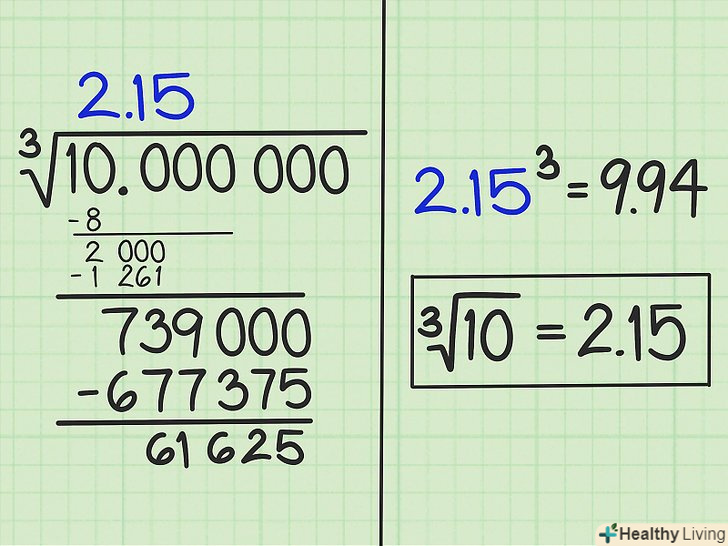
 Помножте останню цифру відповіді на другий множник.після того як Ви знайшли другий множник і третю цифру відповіді, дійте наступним чином:
Помножте останню цифру відповіді на другий множник.після того як Ви знайшли другий множник і третю цифру відповіді, дійте наступним чином:- Помножте останню цифру відповіді на знайдений множник: 135475*5 = 677375.
- Відніміть: 739000-677375 = 61625.
- Подумайте, чи є отримана відповідь досить точною. Для цього піднесіть його в куб:
.
 Запишіть відповідь.Результат, записаний над знаком кореня, є відповіддю з точністю до двох цифр після коми. У нашому прикладі кубічний корінь з 10 дорівнює 2,15. Перевірте відповідь, звівши його в куб: 2,15^3 = 9,94, що приблизно дорівнює 10. Якщо вам потрібна більша точність, продовжуйте обчислення (як описано вище).
Запишіть відповідь.Результат, записаний над знаком кореня, є відповіддю з точністю до двох цифр після коми. У нашому прикладі кубічний корінь з 10 дорівнює 2,15. Перевірте відповідь, звівши його в куб: 2,15^3 = 9,94, що приблизно дорівнює 10. Якщо вам потрібна більша точність, продовжуйте обчислення (як описано вище).
Частина2З 3:
Витяг кубічного кореня методом оцінок
Частина2З 3:
 Використовуйте Куби чисел, щоб визначити верхній і нижній межі.якщо потрібно витягти кубічний корінь практично з будь-якого числа, знайдіть Куби (деяких чисел), які близькі до даного числа.
Використовуйте Куби чисел, щоб визначити верхній і нижній межі.якщо потрібно витягти кубічний корінь практично з будь-якого числа, знайдіть Куби (деяких чисел), які близькі до даного числа.- Наприклад, потрібно витягти кубічний корінь з 600. Оскільки
і
, те значення кубічного кореня з 600 лежить між 8 і 9. Тому використовуйте числа 512 і 729 в якості верхнього і нижнього меж відповіді.
- Наприклад, потрібно витягти кубічний корінь з 600. Оскільки
 Оцініть друге число. перше число Ви знайшли завдяки знанню кубів цілих чисел. Тепер ціле число перетворите в десятковий дріб, приписавши до нього (після десяткової коми) деяку цифру від 0 до 9. Необхідно знайти десятковий дріб, куб якої буде близький, але менше вихідного числа.
Оцініть друге число. перше число Ви знайшли завдяки знанню кубів цілих чисел. Тепер ціле число перетворите в десятковий дріб, приписавши до нього (після десяткової коми) деяку цифру від 0 до 9. Необхідно знайти десятковий дріб, куб якої буде близький, але менше вихідного числа.- У нашому прикладі число 600 знаходиться між числами 512 і 729. Наприклад, до першого знайденого числа (8) припишіть цифру 5. Вийде число 8,5.
 Оцініть отримане число, звівши його в куб. зробіть це, щоб перевірити, що куб близький, але не більше вихідного числа.
Оцініть отримане число, звівши його в куб. зробіть це, щоб перевірити, що куб близький, але не більше вихідного числа.- У нашому прикладі:
- У нашому прикладі:
 Якщо потрібно, оцініть інше число.Порівняйте куб отриманого числа з вихідним числом. Якщо куб отриманого числа більше вихідного числа, спробуйте оцінити менше число. Якщо ж куб отриманого числа набагато менше вихідного числа, оцінюйте великі числа до тих пір, поки куб одного з них не перевищить вихідне число.
Якщо потрібно, оцініть інше число.Порівняйте куб отриманого числа з вихідним числом. Якщо куб отриманого числа більше вихідного числа, спробуйте оцінити менше число. Якщо ж куб отриманого числа набагато менше вихідного числа, оцінюйте великі числа до тих пір, поки куб одного з них не перевищить вихідне число.- У нашому прикладі:
&#gt; 600. Таким чином, оцініть менше число 8,4. Зведіть це число в куб і порівняйте його з вихідним числом:
. Цей результат менше вихідного числа. Таким чином, значення кубічного кореня з 600 лежить між 8,4 і 8,5.
- У нашому прикладі:
 Оцініть наступне число, щоб підвищити точність відповіді.до кожного числа, яке ви оцінили останнім, приписуйте цифру від 0 до 9 до тих пір, поки не отримаєте точну відповідь. У кожному оціночному раунді потрібно знайти верхній і нижній межі, між якими знаходиться вихідне число.
Оцініть наступне число, щоб підвищити точність відповіді.до кожного числа, яке ви оцінили останнім, приписуйте цифру від 0 до 9 до тих пір, поки не отримаєте точну відповідь. У кожному оціночному раунді потрібно знайти верхній і нижній межі, між якими знаходиться вихідне число.- У нашому прикладі:
і
. Вихідне число 600 ближче до 592, ніж до 614. Тому до останнього числа, яке ви оцінили, припишіть цифру, яка ближче до 0, ніж до 9. Наприклад, таким числом є 4. Тому зведіть в куб число 8,44.
- У нашому прикладі:
 Якщо потрібно, оцініть інше число.Порівняйте куб отриманого числа з вихідним числом. Якщо куб отриманого числа більше вихідного числа, спробуйте оцінити менше число. Коротше кажучи, потрібно знайти такі два числа, Куби яких трохи більше і трохи менше вихідного числа.
Якщо потрібно, оцініть інше число.Порівняйте куб отриманого числа з вихідним числом. Якщо куб отриманого числа більше вихідного числа, спробуйте оцінити менше число. Коротше кажучи, потрібно знайти такі два числа, Куби яких трохи більше і трохи менше вихідного числа.- У нашому прикладі
. Це трохи більше вихідного числа, тому оцініть інше (менше) число, наприклад, 8,43:
. Таким чином, значення кубічного кореня з 600 лежить між 8,43 і 8,44.
- У нашому прикладі
 Виконуйте описаний процес до тих пір, поки не отримаєте відповідь, точність якого вас влаштує.оцініть наступне число, порівняйте його з вихідним, потім, якщо потрібно, оцініть інше число і так далі. Зверніть увагу, що кожна додаткова цифра після десяткової коми підвищує точність відповіді.
Виконуйте описаний процес до тих пір, поки не отримаєте відповідь, точність якого вас влаштує.оцініть наступне число, порівняйте його з вихідним, потім, якщо потрібно, оцініть інше число і так далі. Зверніть увагу, що кожна додаткова цифра після десяткової коми підвищує точність відповіді.- У нашому прикладі куб числа 8,43 менше вихідного числа менш ніж на 1. Якщо потрібна велика точність, зведіть в куб число 8,434 і отримаєте, що
, тобто результат менше вихідного числа менш ніж на 0,1.
- У нашому прикладі куб числа 8,43 менше вихідного числа менш ніж на 1. Якщо потрібна велика точність, зведіть в куб число 8,434 і отримаєте, що
Частина3З 3:
Пояснення описаного процесу обчислення
Частина3З 3:
 Згадайте біномінальний ряд.Біномінальний ряд-це результат зведення бінома (двучлена) в деяку ступінь, в даному випадку в куб.щоб зрозуміти описаний тут алгоритм вилучення кубічного кореня, спочатку згадайте, як зводиться в куб двучлен. Швидше за все, ви вивчали це в школі (і, ймовірно, незабаром забули, як більшість людей). Змінними
Згадайте біномінальний ряд.Біномінальний ряд-це результат зведення бінома (двучлена) в деяку ступінь, в даному випадку в куб.щоб зрозуміти описаний тут алгоритм вилучення кубічного кореня, спочатку згадайте, як зводиться в куб двучлен. Швидше за все, ви вивчали це в школі (і, ймовірно, незабаром забули, як більшість людей). Зміннимиі
позначте деякі однозначні числа. Тоді двозначне число можна записати у вигляді бінома
.[9]
- Тут член
представляє собою розряд десятків, тобто якщо
– це будь-яке однозначне число, то
– це вже відповідне двозначне число. Наприклад, якщо
= 2, а
= 6, то
= 26, тобто ви отримали двозначне число 26.[10]
- Тут член

 Зрозумійте алгоритм ділення в стовпчик.зверніть увагу, що описаний тут метод вилучення кубічного кореня дуже нагадує поділ в стовпчик. При розподілі в стовпчик потрібно знайти число (ПРИВАТНЕ), при множенні якого на дільник вийде ділене. В описаному методі в якості приватного виступає результат вилучення кубічного кореня (він записується над знаком кореня). Тобто результат вилучення кубічного кореня можна представити як Біном (10A + B). Точні значення а і в на даному етапі не важливі: просто запам'ятайте, що результат можна записати у вигляді двучлена.[12]
Зрозумійте алгоритм ділення в стовпчик.зверніть увагу, що описаний тут метод вилучення кубічного кореня дуже нагадує поділ в стовпчик. При розподілі в стовпчик потрібно знайти число (ПРИВАТНЕ), при множенні якого на дільник вийде ділене. В описаному методі в якості приватного виступає результат вилучення кубічного кореня (він записується над знаком кореня). Тобто результат вилучення кубічного кореня можна представити як Біном (10A + B). Точні значення а і в на даному етапі не важливі: просто запам'ятайте, що результат можна записати у вигляді двучлена.[12]