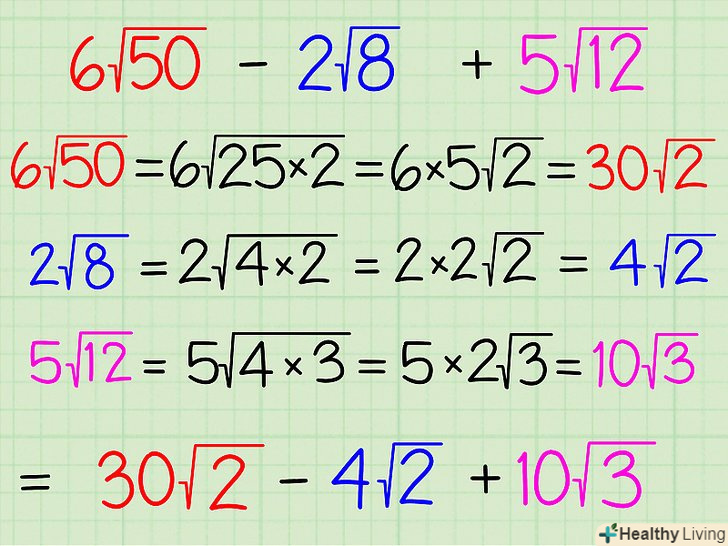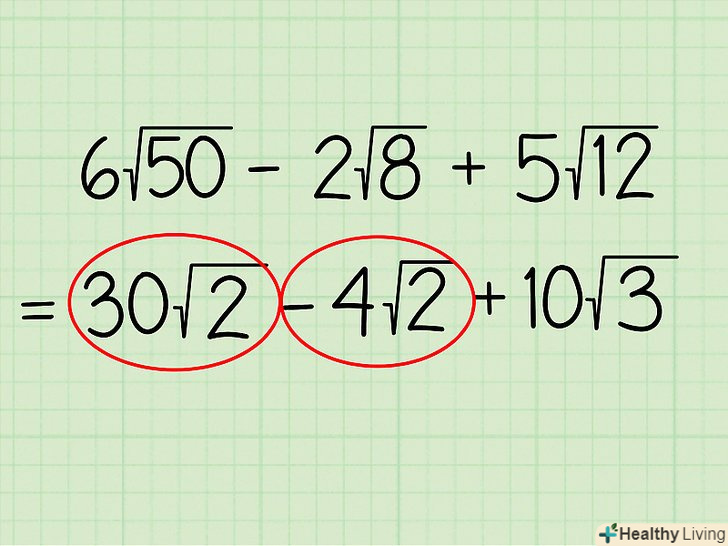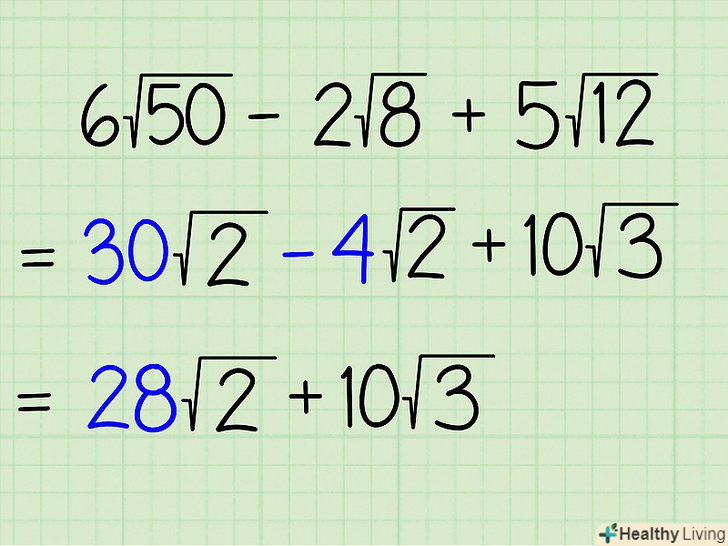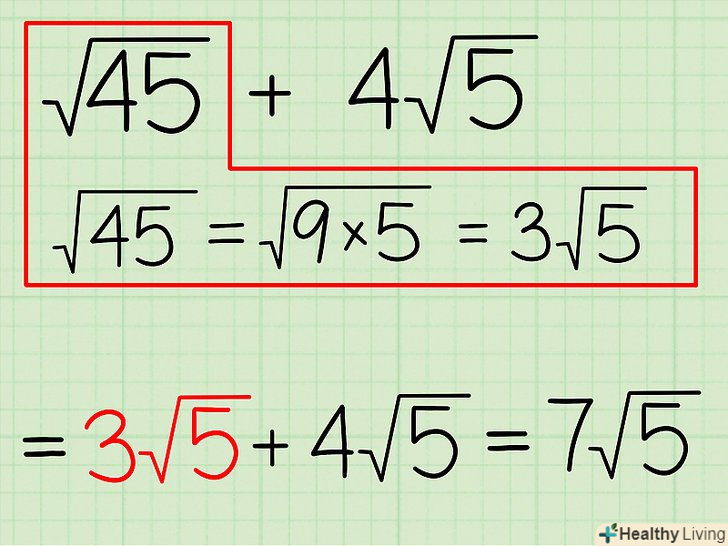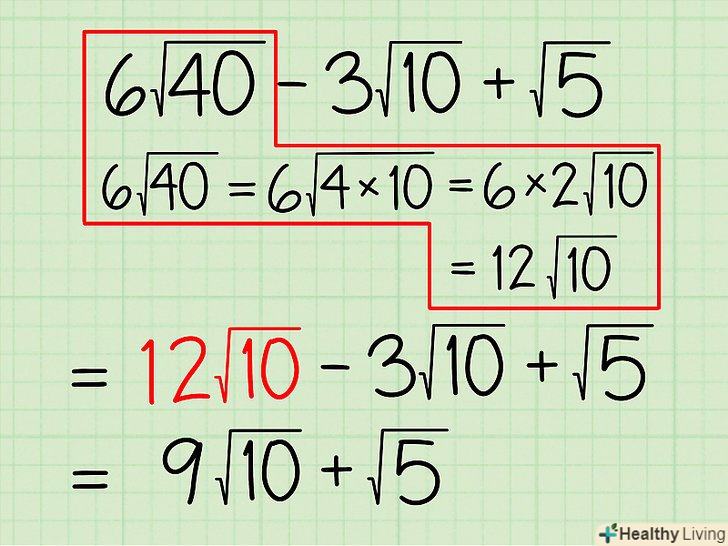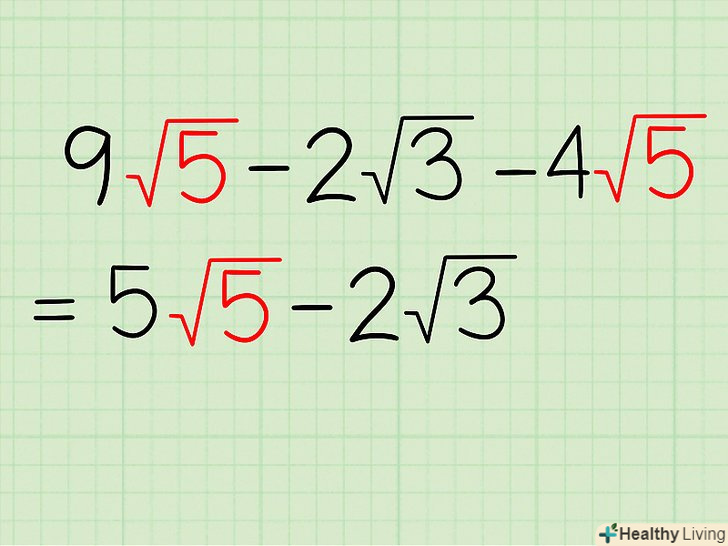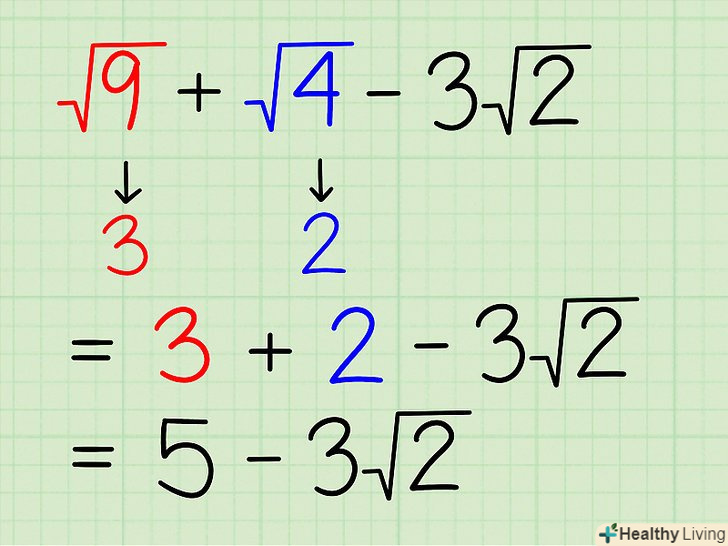Як складати і віднімати квадратні корені: 9 кроків

Складати і віднімати квадратні корені можна тільки за умови, що у них однакове підкорене вираз, тобто ви можете скласти або відняти 2√3 і 4√3, але не 2√3 і 2√5. Ви можете спростити підкорене вираз, щоб привести їх до коріння з однаковими підкореними виразами (а потім скласти або відняти їх).

Частина1 З 2:

Осягаємо основи

Спростіть підкорене вираз(вираз під знаком кореня).для цього розкладіть підкорене число на два множники, один з яких є квадратним числом (число, з якого можна витягти цілий корінь, наприклад, 25 або 9). Після цього витягніть корінь з квадратного числа і запишіть знайдене значення перед знаком кореня (під знаком кореня залишиться другий множник). Наприклад, 6√50 - 2√8 + 5√12. Числа, що стоїть перед знаком кореня, є множниками відповідних коренів, а числа під знаком кореня – це підкорені числа (вирази). Ось як вирішувати це завдання:^{[1]X
Джерело інформації}
- 6√50 = 6√(25 x 2) = (6 x 5)√2 = 30√2. Тут ви розкладаєте 50 на множники 25 і 2; потім з 25 витягаєте корінь, рівний 5, і 5 виносите з-під кореня. Потім 5 множите на 6 (множник біля кореня) і отримуєте 30√2.
- 2√8 = 2√(4 x 2) = (2 x 2)√2 = 4√2. Тут ви розкладаєте 8 на множники 4 і 2; потім з 4 витягаєте корінь, рівний 2, і 2 виносите з-під кореня. Потім 2 множите на 2 (множник біля кореня) і отримуєте 4√2.
- 5√12 = 5√(4 x 3) = (5 x 2)√3 = 10√3. Тут ви розкладаєте 12 на множники 4 і 3; потім з 4 витягаєте корінь, рівний 2, і 2 виносите з-під кореня. Потім 2 множите на 5 (множник біля кореня) і отримуєте 10√3.
Підкресліть коріння, підкорені вирази яких однакові.у нашому прикладі спрощений вираз має вигляд: 30√2 - 4√2 + 10√3. У ньому ви повинні підкреслити перший і другий члени ( 30√2і 4√2), так як у них однакове підкорене число 2. Тільки такі корені ви можете складати і віднімати.
Якщо вам дано вираз з великою кількістю членів, багато з яких мають однакові підкорені вирази, використовуйте одинарне, подвійне, потрійне підкреслення для позначення таких членів, щоб полегшити вирішення цього виразу.
Біля коріння, підкорені вирази яких однакові, складіть або відніміть множники, що стоять перед знаком кореня, а підкорене вираз залиште колишнім (не складайте і не віднімайте підкорені числа!). Ідея в тому, щоб показати, скільки всього коренів з певним підкореним виразом міститься в даному виразі.
- 30√2 - 4√2 + 10√3 =
- (30 - 4)√2 + 10√3 =
- 26√2 + 10√3

Частина2 З 2:

Практикуємося на прикладах

Приклад 1: √(45) + 4√5.
- Спростіть √(45). Розкладіть 45 на множники: √(45) = √(9 x 5).
- Винесіть 3 з-під кореня (√9 = 3): √(45) = 3√5.
- Тепер складіть множники біля коріння: 3√5 + 4√5 = 7√5
Приклад 2: 6√(40) - 3√(10) + √5.
- 6√(40). Розкладіть 40 на множники: 6√(40) = 6√(4 x 10).
- Винесіть 2 з-під кореня (√4 = 2): 6√(40) = 6√(4 x 10) = (6 x 2)√10.
- Перемножте множники перед коренем і отримаєте 12√10.
- Тепер вираз можна записати у вигляді 12√10 - 3√(10) + √5. Так як у перших двох членів однакові підкорені числа, ви можете відняти другий член з першого, а перший залишити без змін.
- Ви отримаєте: (12-3)√10 + √5 = 9√10 + √5.
Приклад 3. 9√5 -2√3 - 4√5. Тут жодне з підкорених виразів не можна розкласти на множники, тому спростити цей вираз не вийде. Ви можете відняти третій член з першого (так як у них однакові підкорені числа), а другий член залишити без змін. Ви отримаєте: (9-4)√5 -2√3 = 5√5 - 2√3.
Приклад 4. √9 + √4 - 3√2.
- √9 = √(3 х 3) = 3.
- √4 = √(2 х 2) = 2.
- Тепер ви можете просто скласти 3 + 2, щоб отримати 5.
- Остаточна відповідь: 5-3√2.
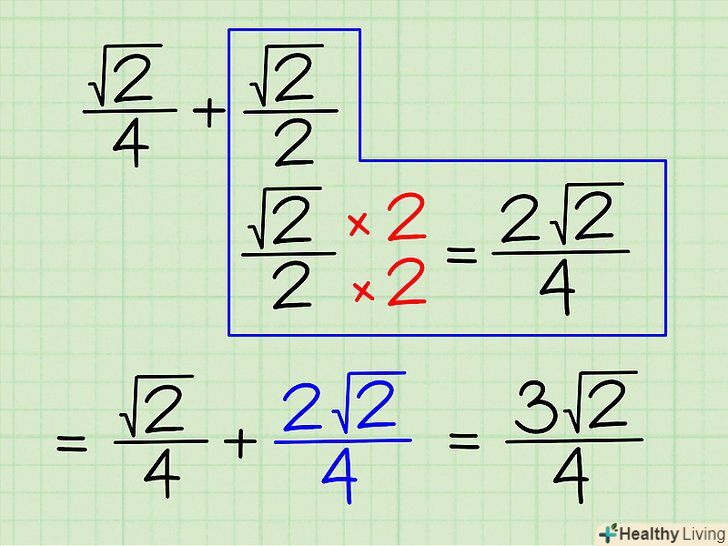
Приклад 5.Вирішіть вираз, що містить коріння і дроби. Ви можете складати і обчислювати тільки ті дроби, у яких загальний (однаковий) знаменник. Дано вираз (√2)/4 + (√2)/2.
- Знайдіть найменший спільний знаменник цих дробів. Це число, яке ділиться на кожен знаменник. У нашому прикладі на 4 і на 2 ділиться число 4.
- Тепер другий дріб помножте на 2/2 (щоб привести її до спільного знаменника; перша дріб вже приведена до нього): (√2) / 2 х 2/2 = (2√2)/4.
- Складіть чисельники дробів, а знаменник залиште колишнім: (√2)/4 + (2√2)/4 = (3√2)/4.

Поради

Перед підсумовуванням або відніманням коренів обов'язково спростіть (якщо можливо) підкорені вирази.

Попередження

Ніколи не підсумовуйте і не віднімайте коріння з різними підкореними виразами.
Ніколи не підсумовуйте і не віднімайте ціле число і корінь, наприклад,3 + (2x)^1/2.
- Примітка: «х "в одному другому ступені і квадратний корінь з" х " - це одне і те ж (тобто x^1/2 = √х).