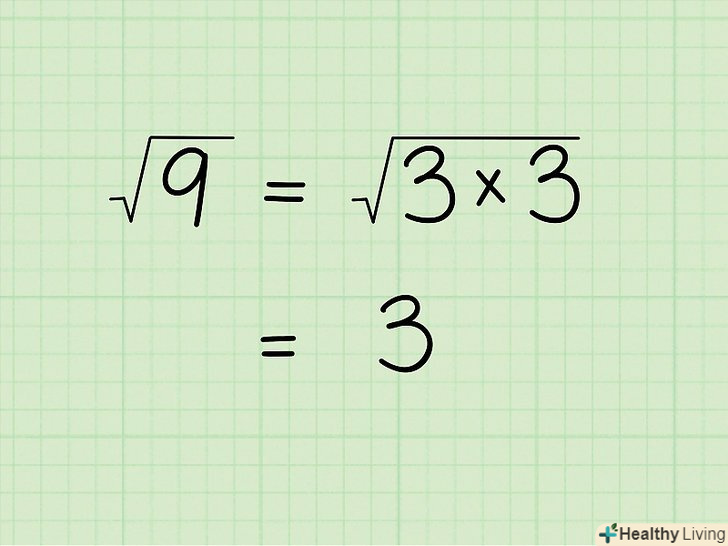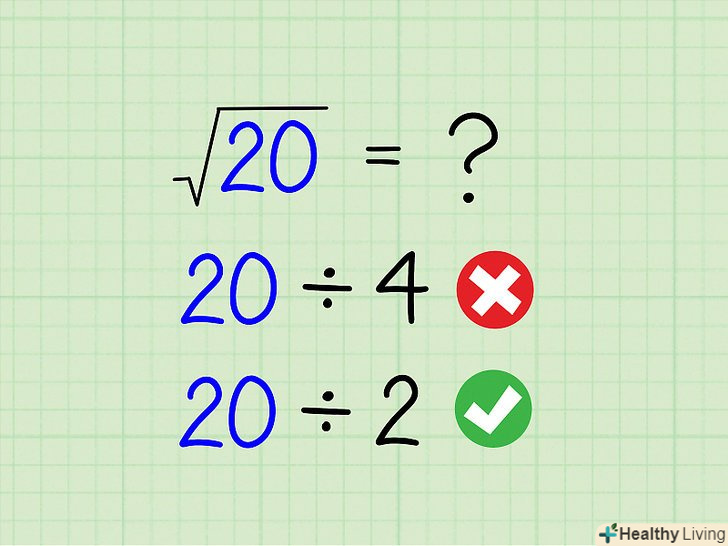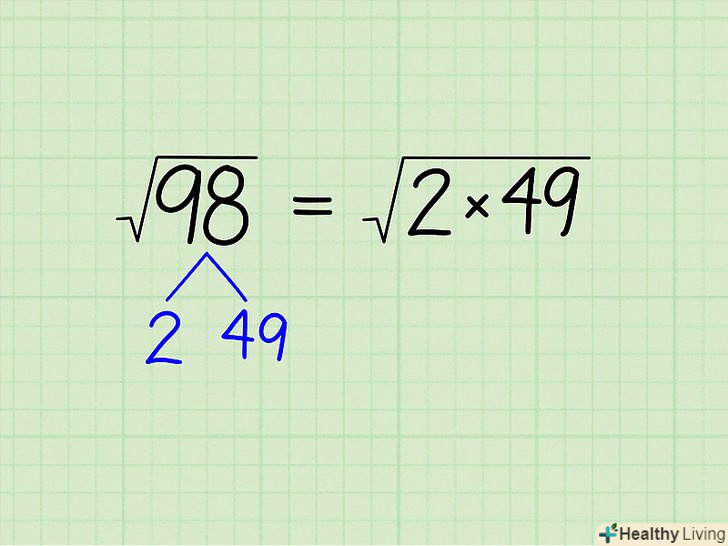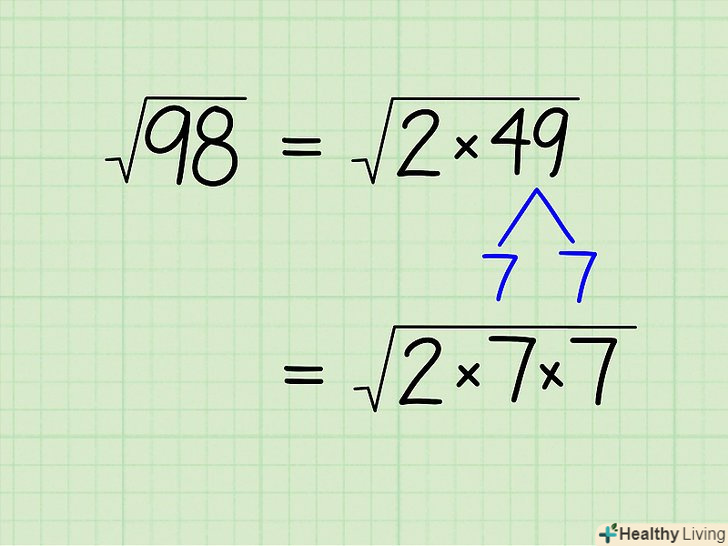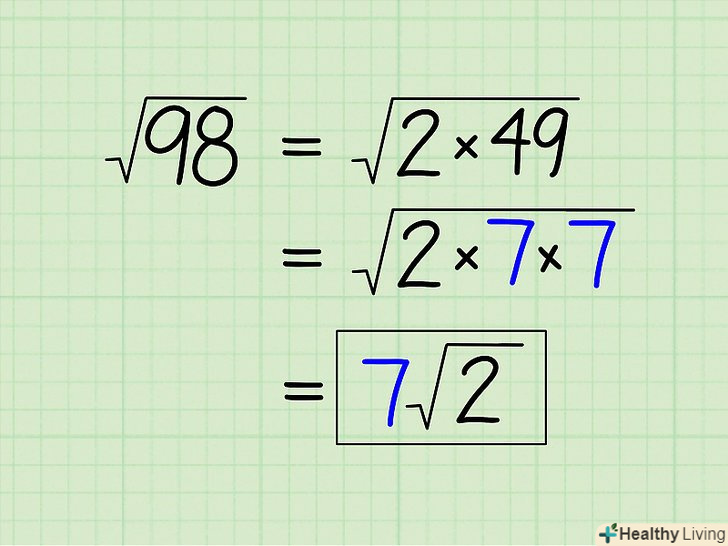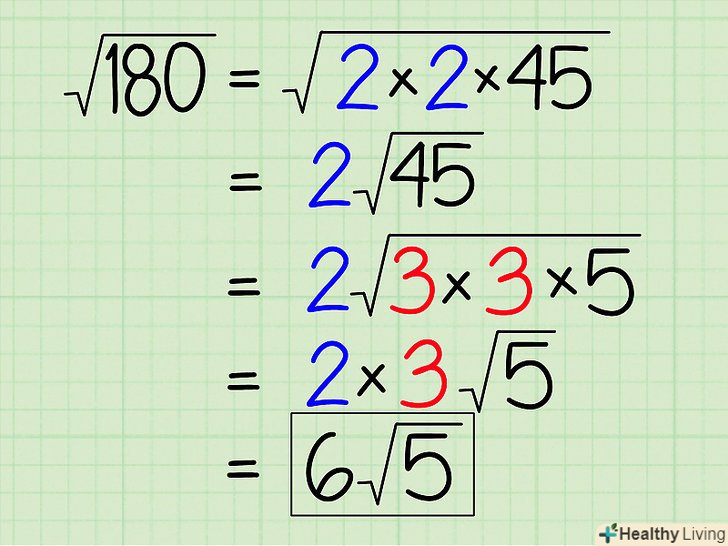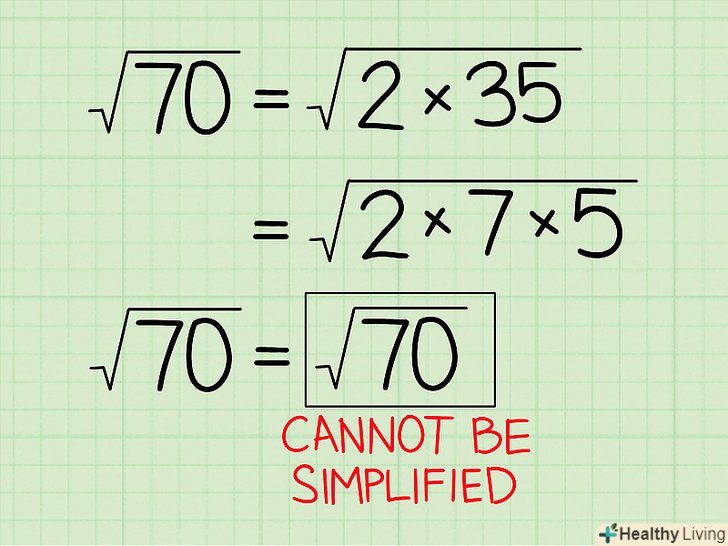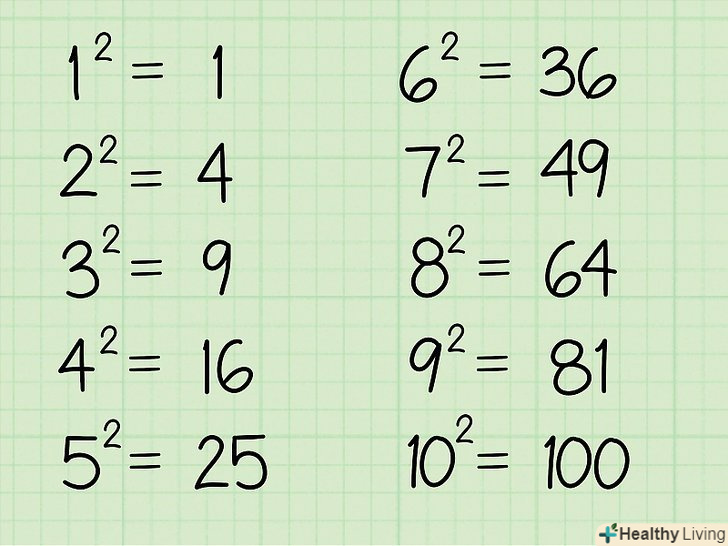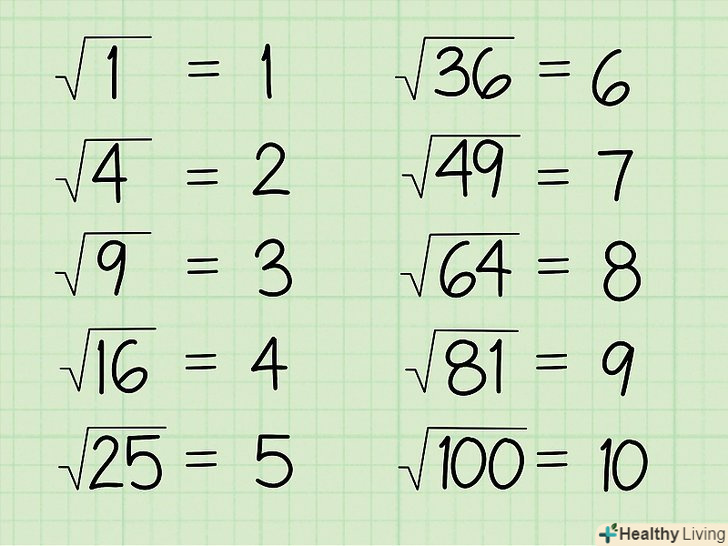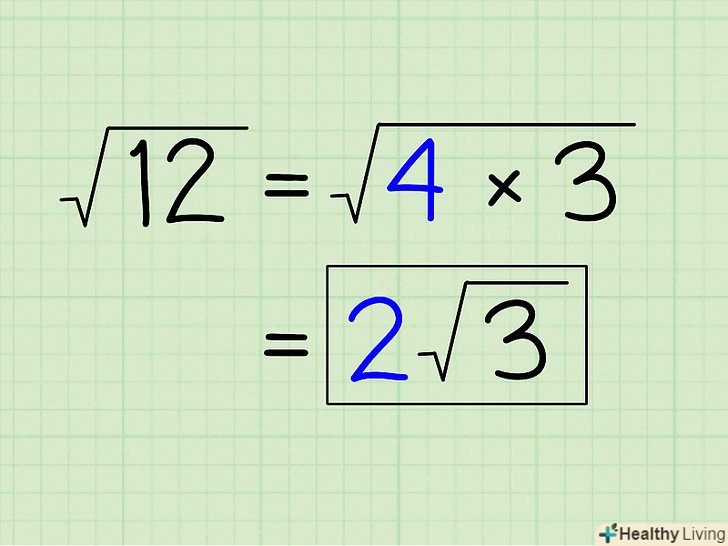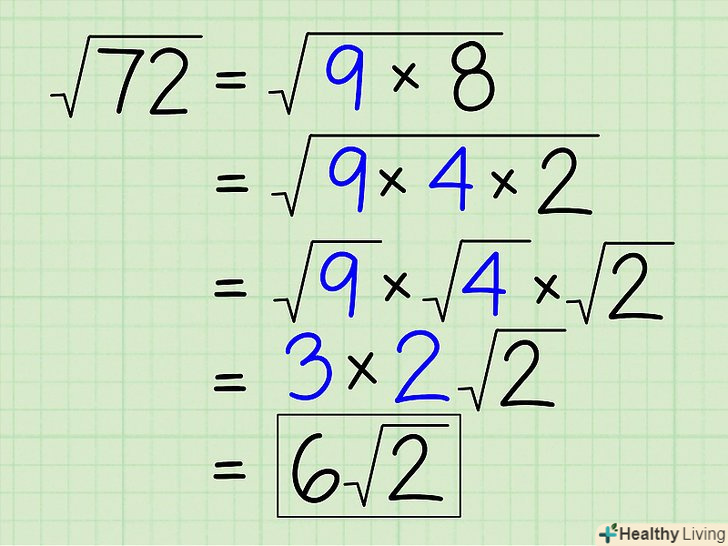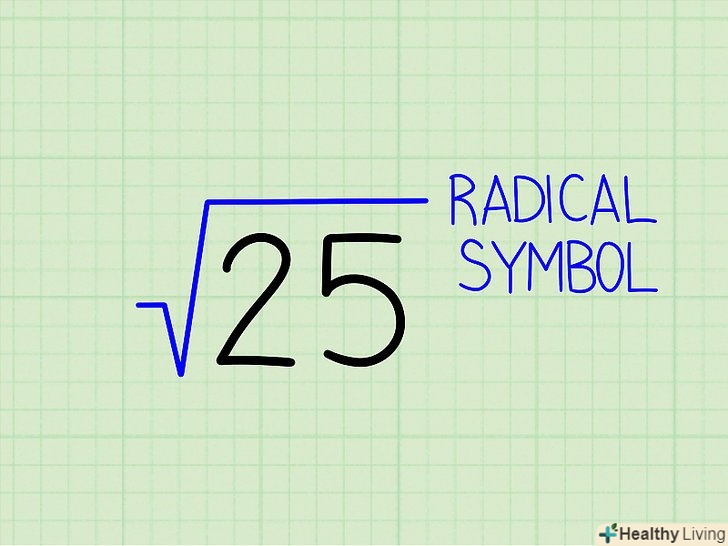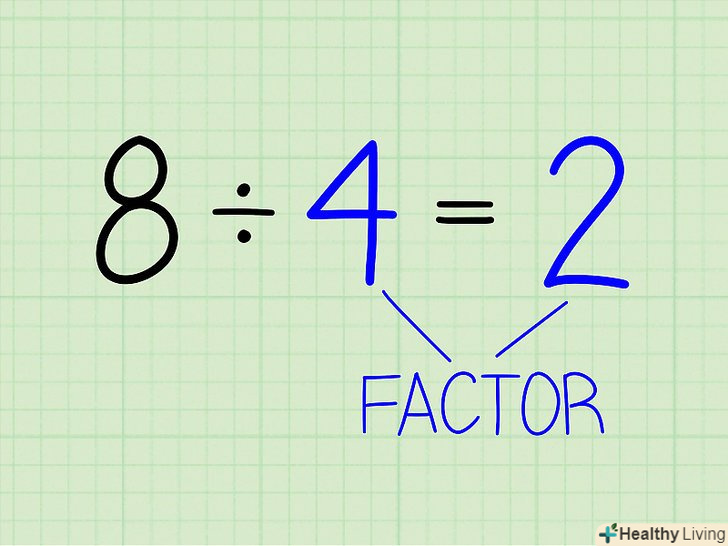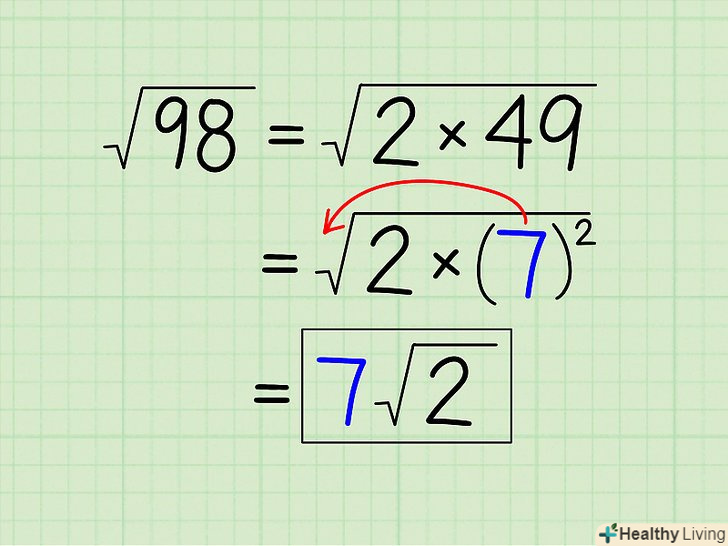Спростити квадратний корінь зовсім не так складно, як може здатися. Потрібно просто розкласти число на множники і витягти з-під знака кореня повні квадрати. Запам'ятавши кілька найпоширеніших квадратів і навчившись розкладати число на множники, ви зможете запросто спрощувати квадратні корені.
Кроки
Метод1З 3:
Розкладання на множники
Метод1З 3:
 Мета спрощення квадратного кореня-це переписати його в такій формі, яку простіше використовувати в обчисленнях.розкладання числа на множники - це знаходження двох або декількох чисел, які при перемноженні дадуть вихідне число, наприклад, 3 х 3 = 9. Знайшовши множники, ви зможете спростити квадратний корінь або взагалі позбутися від нього. Наприклад, √9 = √(3x3) = 3.[1]
Мета спрощення квадратного кореня-це переписати його в такій формі, яку простіше використовувати в обчисленнях.розкладання числа на множники - це знаходження двох або декількох чисел, які при перемноженні дадуть вихідне число, наприклад, 3 х 3 = 9. Знайшовши множники, ви зможете спростити квадратний корінь або взагалі позбутися від нього. Наприклад, √9 = √(3x3) = 3.[1] Якщо підкорене число парне, розділіть його на 2. якщо підкорене число непарне, спробуйте розділити його на 3 (якщо число на 3 не ділиться, діліть його на 5, 7 і так далі за списком простих чисел). Діліть підкорене число виключно на прості числа, так як будь-яке число можна розкласти на прості множники. Наприклад, вам не потрібно ділити підкорене число на 4, так як 4 ділиться на 2, а ви вже розділили підкорене число на 2.[2]
Якщо підкорене число парне, розділіть його на 2. якщо підкорене число непарне, спробуйте розділити його на 3 (якщо число на 3 не ділиться, діліть його на 5, 7 і так далі за списком простих чисел). Діліть підкорене число виключно на прості числа, так як будь-яке число можна розкласти на прості множники. Наприклад, вам не потрібно ділити підкорене число на 4, так як 4 ділиться на 2, а ви вже розділили підкорене число на 2.[2]- 2
- 3
- 5
- 7
- 11
- 13
- 17
 Перепишіть задачу як корінь з добутку двох чисел.наприклад, спростимо √98: 98 ÷ 2 = 49, тому 98 = 2 x 49. Перепишіть завдання так: √98 = √(2 x 49).[3]
Перепишіть задачу як корінь з добутку двох чисел.наприклад, спростимо √98: 98 ÷ 2 = 49, тому 98 = 2 x 49. Перепишіть завдання так: √98 = √(2 x 49).[3] Продовжуйте розкладання чисел до тих пір, поки під коренем не залишиться добуток двох однакових чисел та інших чисел.це має сенс, якщо задуматися про сенс квадратного кореня: √(2 х 2) дорівнює числу, яке, будучи помноженим саме на себе, дорівнюватиме 2 х 2. Очевидно, що це число 2! Повторіть описані вище дії для нашого прикладу: √(2 х 49).
Продовжуйте розкладання чисел до тих пір, поки під коренем не залишиться добуток двох однакових чисел та інших чисел.це має сенс, якщо задуматися про сенс квадратного кореня: √(2 х 2) дорівнює числу, яке, будучи помноженим саме на себе, дорівнюватиме 2 х 2. Очевидно, що це число 2! Повторіть описані вище дії для нашого прикладу: √(2 х 49).- 2 вже максимально спрощено, так як це просте число (Дивіться список простих чисел вище). Тому розкладіть на множники число 49.
- 49 на 2, 3, 5 не ділиться. Тому переходите до наступного простого числа-7.
- 49 ÷ 7 = 7, тому 49 = 7 x 7.
- Перепишіть завдання так: √(2 x 49) = √(2 x 7 x 7).
 Спростіть квадратний корінь.Так як під коренем знаходиться добуток 2 і двох однакових чисел (7), ви можете винести таке число за знак кореня. У нашому прикладі: √(2 x 7 x 7) = √(2)√(7 x 7) = √(2) x 7 = 7√(2).[4]
Спростіть квадратний корінь.Так як під коренем знаходиться добуток 2 і двох однакових чисел (7), ви можете винести таке число за знак кореня. У нашому прикладі: √(2 x 7 x 7) = √(2)√(7 x 7) = √(2) x 7 = 7√(2).[4]- Як тільки під коренем ви отримали два однакових числа, ви можете зупинитися з розкладанням чисел на множники (якщо їх все ще можна розкласти). Наприклад, √(16) = √(4 х 4) = 4. Якщо ви продовжите розкладання чисел на множники, Ви отримаєте ту ж відповідь, але зробите більше обчислень: √(16) = √(4 х 4) = √(2 х 2 х 2 х 2) = √(2 х 2) √(2 х 2) = 2 х 2 = 4.
 Деякі корені можна спрощувати багаторазово. в цьому випадку числа, що виносяться з-під знака кореня, і числа, що стоять перед коренем, перемножуються. Наприклад:
Деякі корені можна спрощувати багаторазово. в цьому випадку числа, що виносяться з-під знака кореня, і числа, що стоять перед коренем, перемножуються. Наприклад:- √180 = √(2 x 90)
- √180 = √(2 x 2 x 45)
- √180 = 2√45, але 45 можна розкласти на множники і ще раз спростити корінь.
- √180 = 2√(3 x 15)
- √180 = 2√(3 x 3 x 5)
- √180 = (2)(3√5)
- √180 = 6√5
 Якщо ви не можете отримати два однакових числа під знаком кореня, то такий корінь спростити не можна.якщо ви розклали підкорене вираз на твір простих множників і серед них немає двох однакових чисел, то такий корінь спростити не можна. Наприклад, спробуємо спростити √70:[5]
Якщо ви не можете отримати два однакових числа під знаком кореня, то такий корінь спростити не можна.якщо ви розклали підкорене вираз на твір простих множників і серед них немає двох однакових чисел, то такий корінь спростити не можна. Наприклад, спробуємо спростити √70:[5]- 70 = 35 x 2, тому √70 = √(35 x 2)
- 35 = 7 x 5, тому √(35 x 2) = √(7 x 5 x 2)
- Всі три множники є простими, тому їх більше не можна розкласти на множники. Всі три множника різні, тому ви не зможете винести ціле число з-під знака кореня. Отже, √70 спростити не можна.
Метод2 З 3:
Повний квадрат
Метод2 З 3:
 Запам'ятайте кілька квадратів простих чисел. Квадрат числа виходить при його зведенні в другу ступінь, тобто множенні на саме себе. Наприклад, 25-повний квадрат, тому що 5 x 5 (52) = 25. Запам'ятавши хоча б десяток повних квадратів, ви зможете швидко спрощувати коріння. Ось перші десять повних квадратів:
Запам'ятайте кілька квадратів простих чисел. Квадрат числа виходить при його зведенні в другу ступінь, тобто множенні на саме себе. Наприклад, 25-повний квадрат, тому що 5 x 5 (52) = 25. Запам'ятавши хоча б десяток повних квадратів, ви зможете швидко спрощувати коріння. Ось перші десять повних квадратів:- 12 = 1
- 22 = 4
- 32 = 9
- 42 = 16
- 52 = 25
- 62 = 36
- 72 = 49
- 82 = 64
- 92 = 81
- 102 = 100
 Якщо під знаком квадратного кореня ви бачите повний квадрат, то позбудьтеся від знака кореня (√) і запишіть квадратний корінь цього повного квадрата.наприклад, якщо під знаком квадратного кореня знаходиться число 25, то такий корінь дорівнює 5, так як 25 є повним квадратом.
Якщо під знаком квадратного кореня ви бачите повний квадрат, то позбудьтеся від знака кореня (√) і запишіть квадратний корінь цього повного квадрата.наприклад, якщо під знаком квадратного кореня знаходиться число 25, то такий корінь дорівнює 5, так як 25 є повним квадратом.- √1 = 1
- √4 = 2
- √9 = 3
- √16 = 4
- √25 = 5
- √36 = 6
- √49 = 7
- √64 = 8
- √81 = 9
- √100 = 10
 Розкладіть число під знаком кореня на добуток повного квадрата та іншого числа.якщо ви помітили, що підкорене вираз можна розкласти на твір повного квадрата і якогось числа, то ви заощадите час і зусилля. Ось кілька прикладів: [6]
Розкладіть число під знаком кореня на добуток повного квадрата та іншого числа.якщо ви помітили, що підкорене вираз можна розкласти на твір повного квадрата і якогось числа, то ви заощадите час і зусилля. Ось кілька прикладів: [6]- √50 = √(25 х 2) = 5√2. Якщо підкорене число закінчується на 25, 50 або 75, ви завжди можете розкласти його на твір 25 і якогось числа.
- √1700 = √(100 х 17) = 10√17. Якщо підкорене число закінчується на 00, ви завжди можете розкласти його на добуток 100 і якогось числа.
- √72 = √(9 х 8) = 3√8. Якщо сума цифр підкореного числа дорівнює 9, ви завжди можете розкласти його на добуток 9 і якогось числа.
- √12 = √(4 х 3) = 2√3. Завжди перевіряйте, чи діляться підкорені числа на 4.
 Розкладіть підкорене число на добуток декількох повних квадратів.в цьому випадку винесіть їх з-під знака кореня і перемножте. Наприклад:
Розкладіть підкорене число на добуток декількох повних квадратів.в цьому випадку винесіть їх з-під знака кореня і перемножте. Наприклад:- √72 = √(9 x 8)
- √72 = √(9 x 4 x 2)
- √72 = √(9) x √(4) x √(2)
- √72 = 3 x 2 x √2
- √72 = 6√2
Метод3 З 3:
Термінологія
Метод3 З 3:
 √ - це знак квадратного кореня.наприклад, в √25, « √ » — це знак квадратного кореня.[7]
√ - це знак квадратного кореня.наприклад, в √25, « √ » — це знак квадратного кореня.[7] Під знаком кореня записується підкорене вираз. наприклад, " 25 " - це підкорене вираз (число) в √25.[8]
Під знаком кореня записується підкорене вираз. наприклад, " 25 " - це підкорене вираз (число) в √25.[8] Коефіцієнт-це число, що стоїть перед знаком кореня (зліва від нього).це число, на яке множиться квадратний корінь; воно записується зліва від знака √. Наприклад «» 7 " — це коефіцієнт в 7√2.
Коефіцієнт-це число, що стоїть перед знаком кореня (зліва від нього).це число, на яке множиться квадратний корінь; воно записується зліва від знака √. Наприклад «» 7 " — це коефіцієнт в 7√2. Множник-ціле число, одержуване при діленні іншого числа. 2-множник 8, так як 8 ÷ 4 = 2, а 3 не є множником 8, так як 8 на 3 не ділиться (націлено). 5-множник 25, так як 5 x 5 = 25.
Множник-ціле число, одержуване при діленні іншого числа. 2-множник 8, так як 8 ÷ 4 = 2, а 3 не є множником 8, так як 8 на 3 не ділиться (націлено). 5-множник 25, так як 5 x 5 = 25. Зрозумійте сенс спрощення квадратного кореня.спрощення квадратного кореня-це знаходження серед множників підкореного виразу повних квадратів і їх витяг з-під кореня. Якщо число є повним квадратом, то знак кореня зникне, як тільки ви запишете його корінь. Наприклад, √98 може бути спрощений до 7√2.
Зрозумійте сенс спрощення квадратного кореня.спрощення квадратного кореня-це знаходження серед множників підкореного виразу повних квадратів і їх витяг з-під кореня. Якщо число є повним квадратом, то знак кореня зникне, як тільки ви запишете його корінь. Наприклад, √98 може бути спрощений до 7√2.
Поради
- Для знаходження повного квадрата (як одного з множників підкореного виразу) просто перегляньте список повних квадратів, починаючи з повного квадрата, найближчого до підкореного числа (і далі в порядку зменшення). Шукаючи повний квадрат в числі 27, почніть з повного квадрата 25, потім 16, і зупиніться на 9.
Попередження
- Ні за яких обставин у вас не повинна з'явитися десятковий дріб!
- Калькулятори можуть бути корисні для обчислень з великими підкореними числами, але краще практикуватися в спрощенні коренів вручну.
Джерела
- ↑ Https://www.khanacademy.org/math/algebra/rational-exponents-and-radicals/alg1-simplify-square-roots/v/simplifying-square-roots-1
- ↑ Https://www.khanacademy.org/math/algebra/rational-exponents-and-radicals/alg1-simplify-square-roots/v/simplifying-square-roots-1
- ↑ Https://www.khanacademy.org/math/algebra/rational-exponents-and-radicals/alg1-simplify-square-roots/v/simplifying-square-roots-1
- ↑ Https://www.khanacademy.org/math/algebra/rational-exponents-and-radicals/alg1-simplify-square-roots/v/simplifying-square-roots-1
- ↑ Https://www.khanacademy.org/math/algebra/rational-exponents-and-radicals/alg1-simplify-square-roots/v/simplifying-square-roots-1
- ↑ Https://mathbitsnotebook.com/Algebra1/Radicals/RADSimplifyingRadicals.html
- ↑ Http://www.mathwords.com/r/radical.htm
- ↑ Http://www.mathwords.com/r/radicand.htm