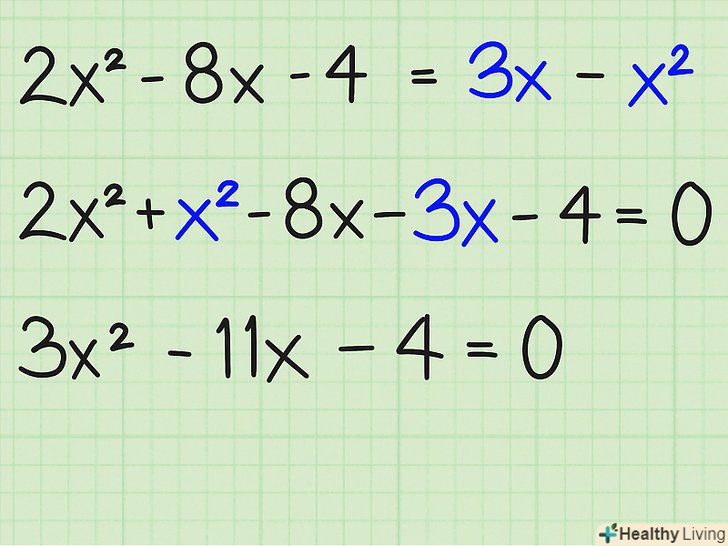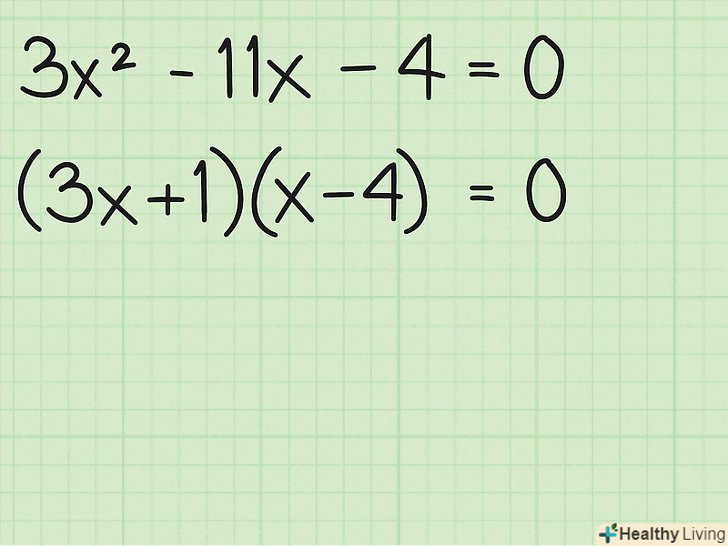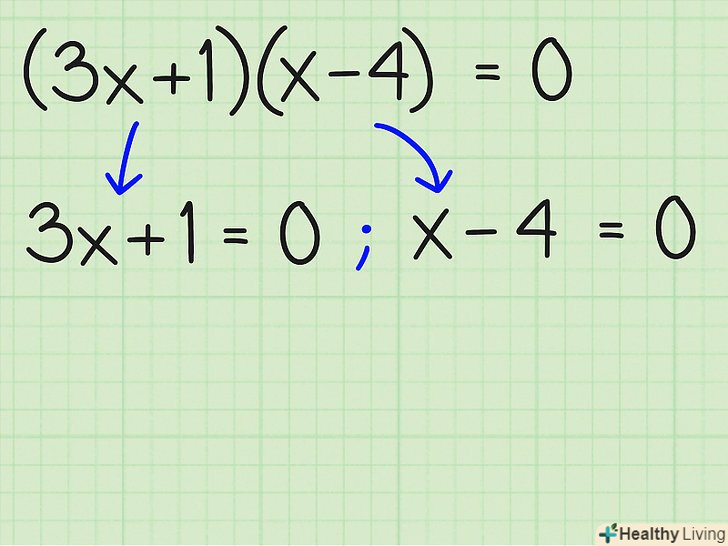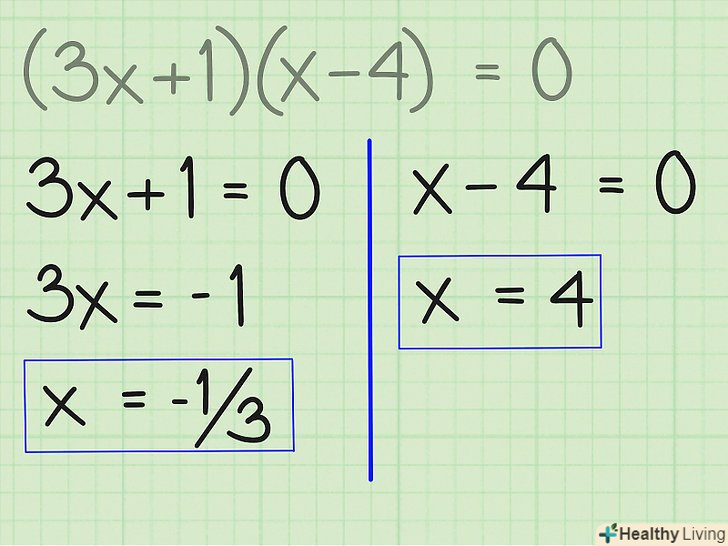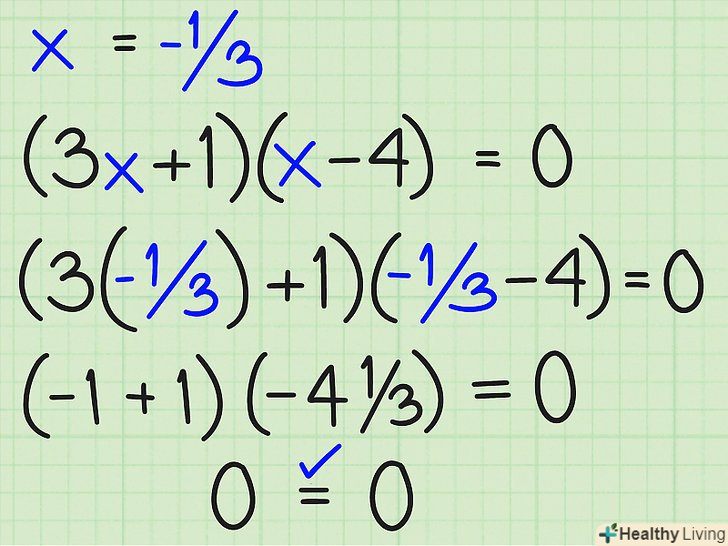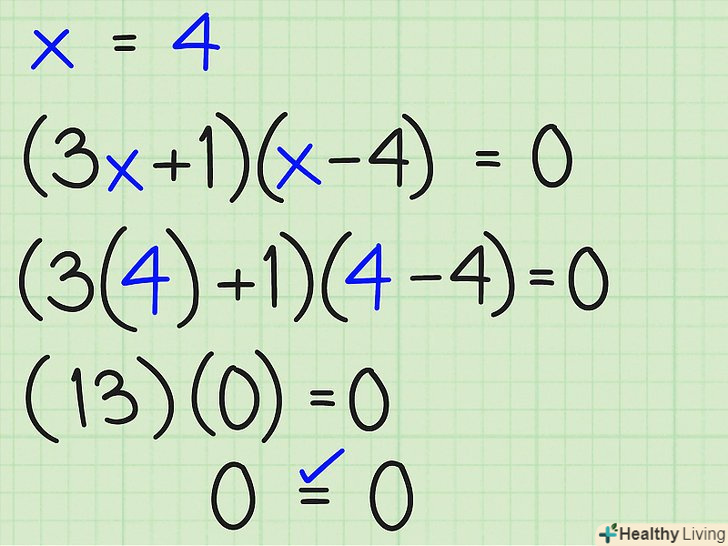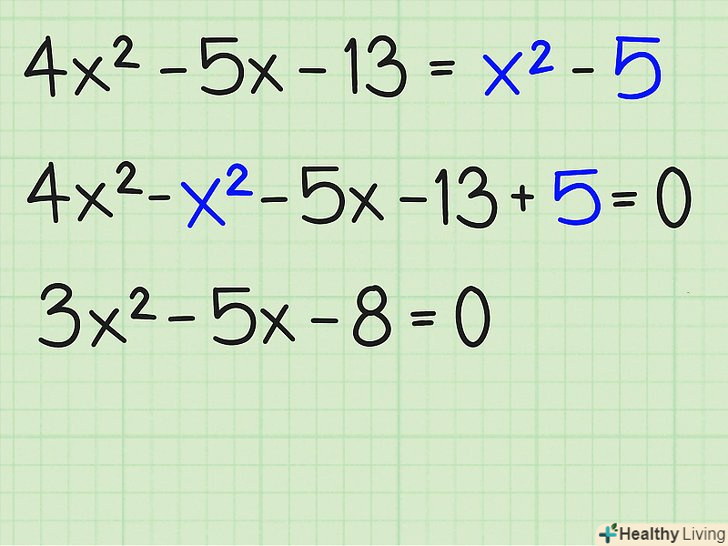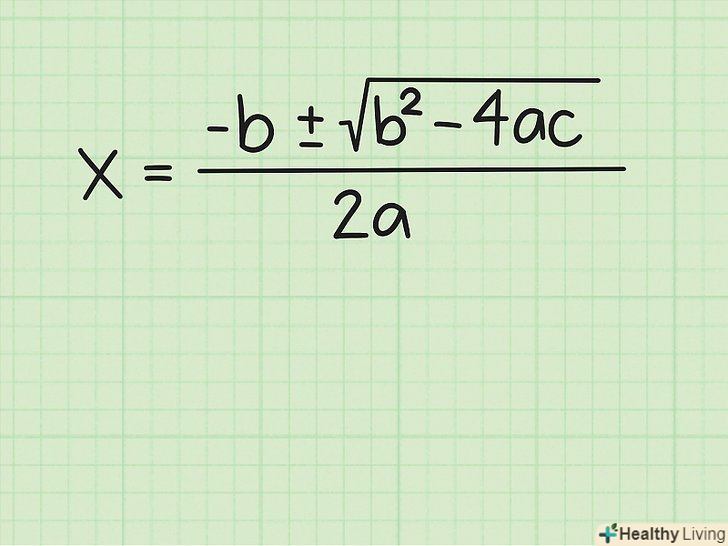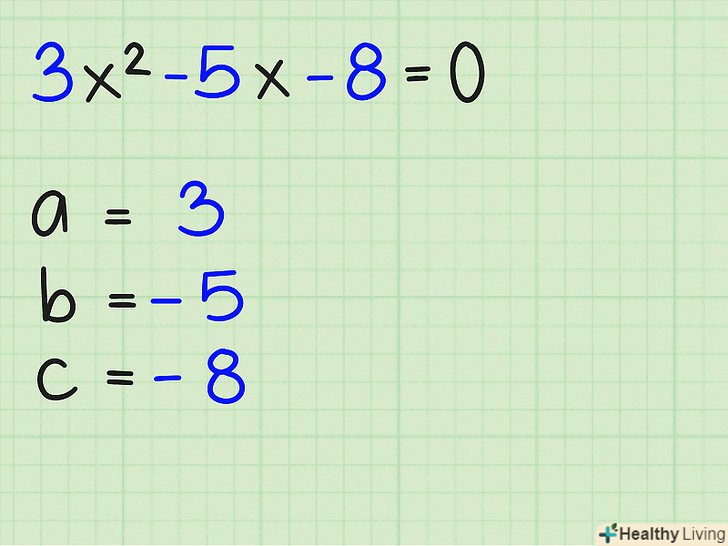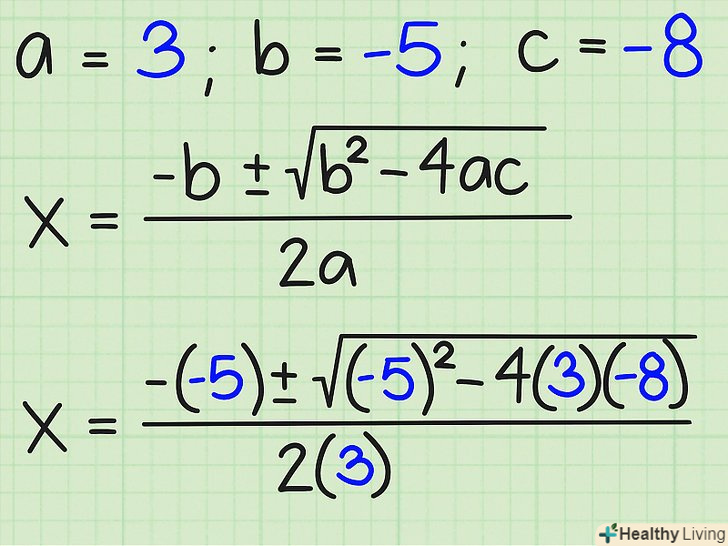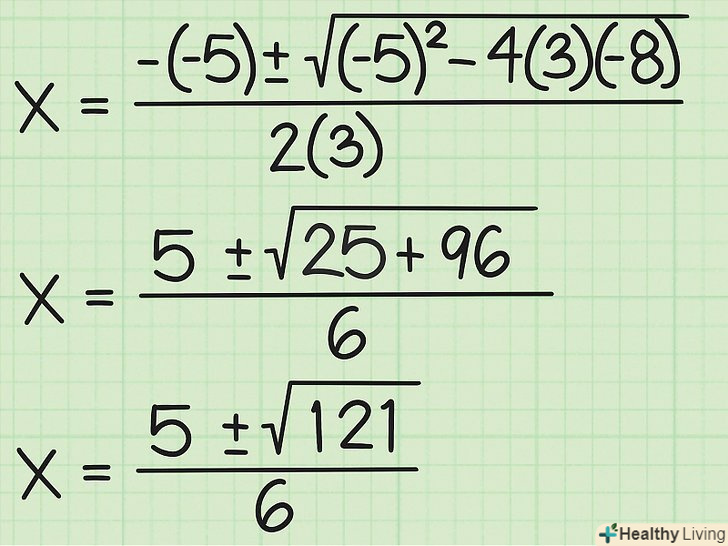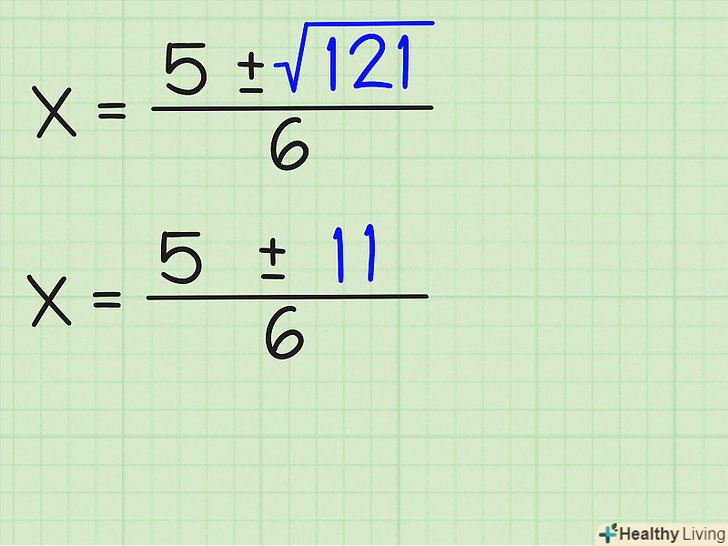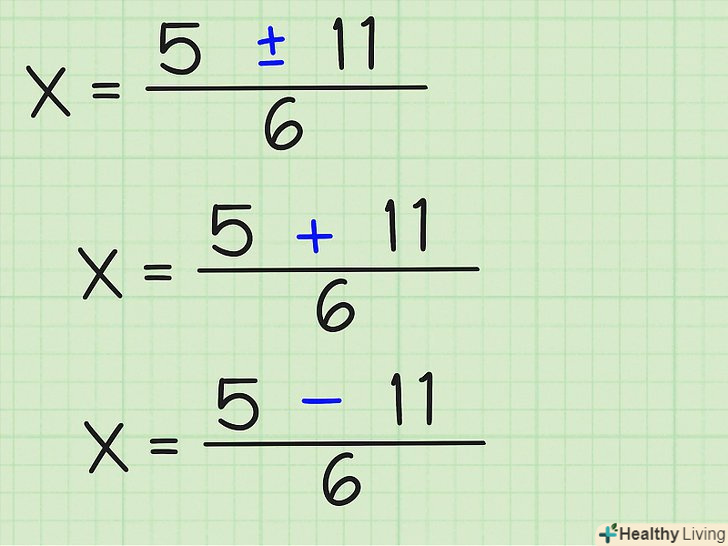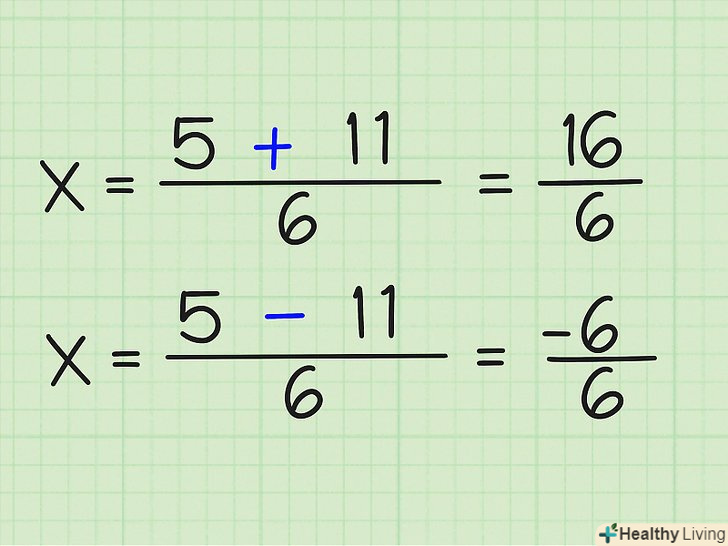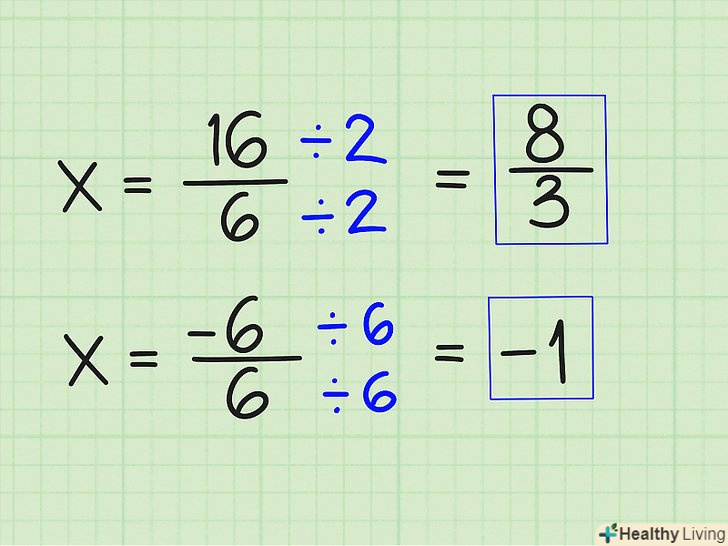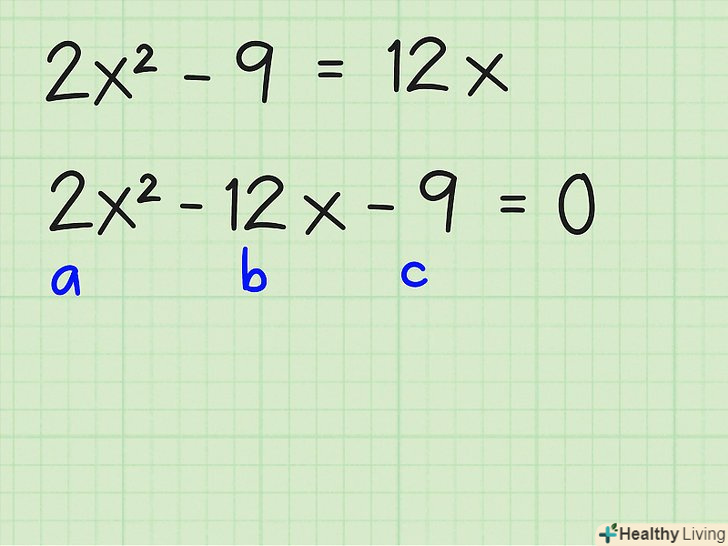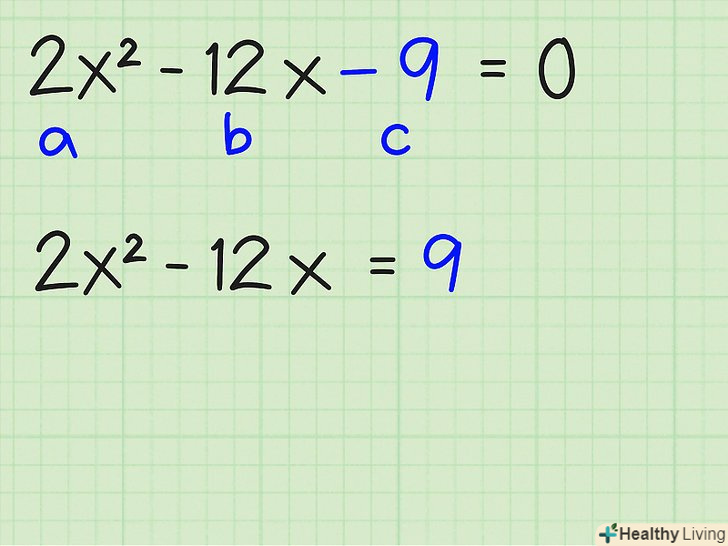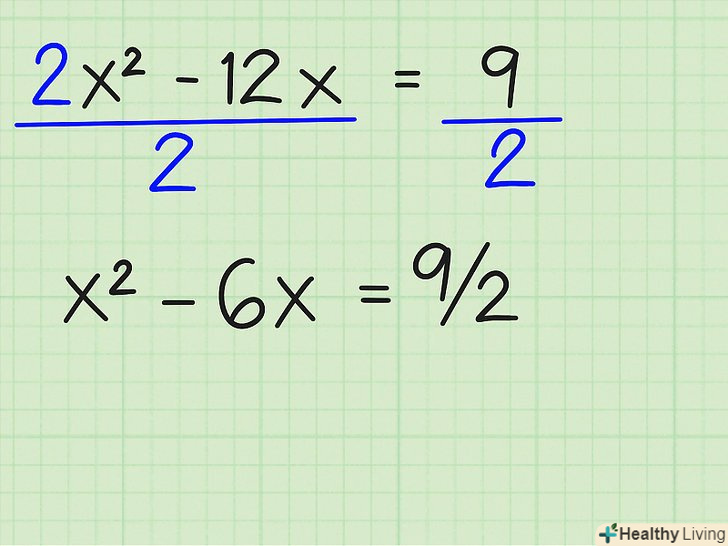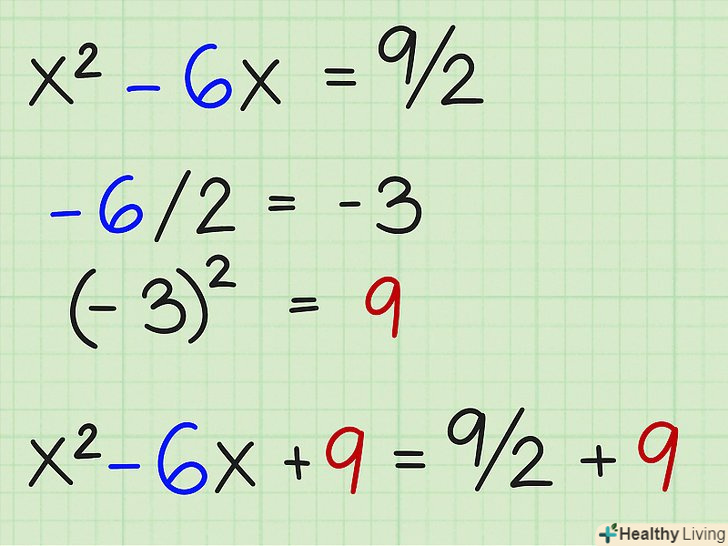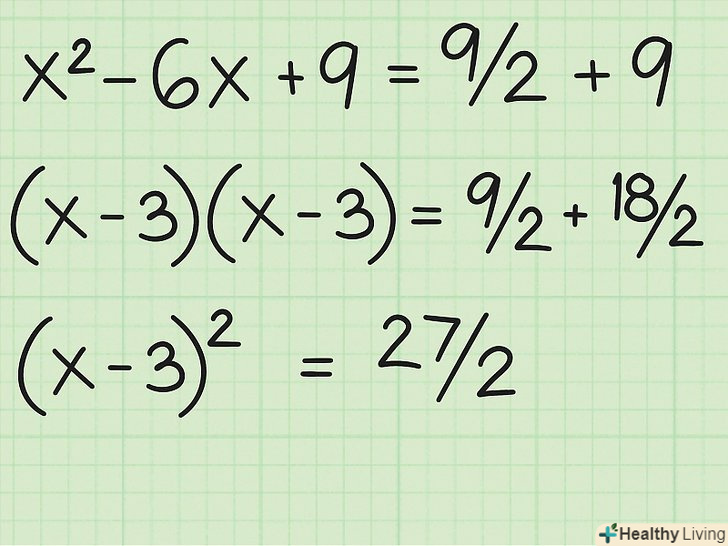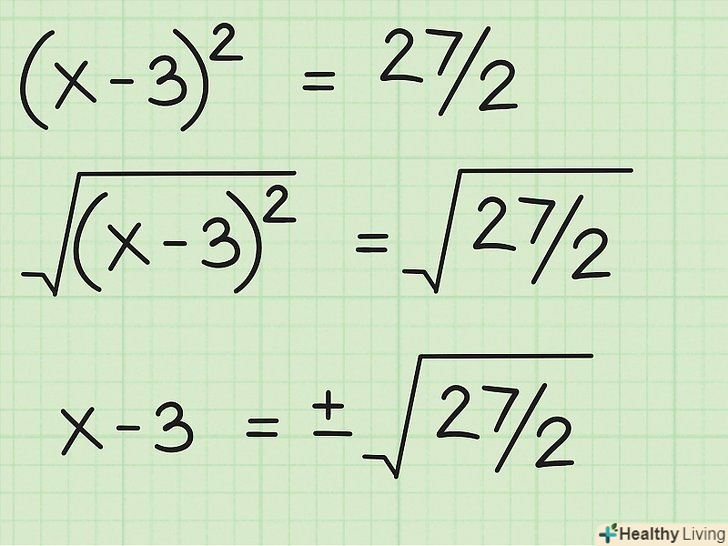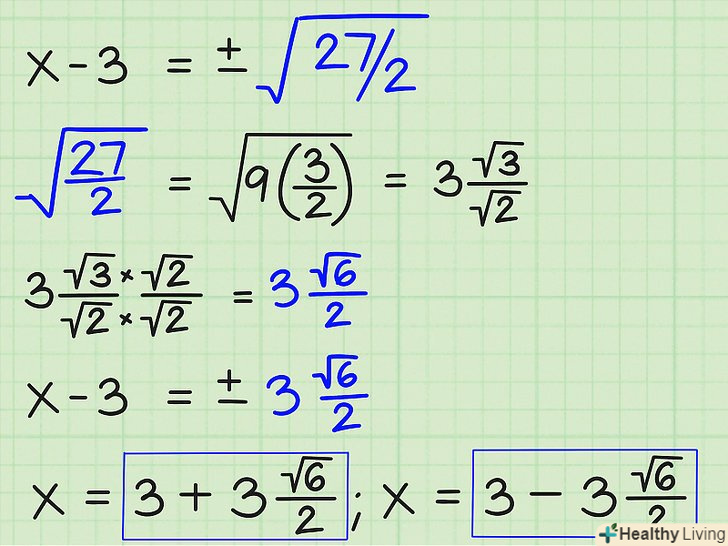1. Головна
    2. Математика
    3. Як вирішувати квадратні рівняння-

Як вирішувати квадратні рівняння-

Квадратним рівнянням називається таке рівняння, в якому найбільше значення ступеня змінної дорівнює 2. Існують три основні способи вирішення квадратних рівнянь: якщо можливо, розкласти квадратне рівняння на множники, використовувати формулу коренів квадратного рівняння або доповнити до повного квадрата. Хочете дізнатися, як же все це робиться? Читайте далі.

Метод1З 3:
Розкладання рівняння на множники

  1. Складіть всі схожі елементи і перенесіть в одну частину рівняння. це і буде першим кроком, значення при цьому має залишатися позитивним. Складіть або відніміть всі значення , і постійних, перенісши все в одну частину і залишивши 0 в інший. Ось як це робиться: [1]
  2. Розкладіть вираз на множники. для цього потрібно використовувати значення (3), постійні значення (-4), вони повинні перемножуватися і утворювати -11. Ось як це зробити:
    • має тільки два можливих множника: і , так що їх можна записати в дужках: .
    • Далі, підставляючи множники 4, знайдемо комбінацію, при множенні дає-11x. можна використовувати комбінацію 4 і 1, або 2 і 2, так як і те, і інше дає 4. Пам'ятайте, що значення повинні бути негативні, адже у нас -4.
    • Методом проб і помилок ви отримаєте комбінацію . При множенні отримуємо . Сполучити і , отримуємо середній член , який ми і шукали. Квадратне рівняння розкладено на множники.
    • Для прикладу спробуємо невідповідну комбінацію: ( = . Об'єднавши, отримаємо . Хоча множники -2 і 2 при множенні дають -4, середній член не підходить, адже ми хотіли отримати , а не .
  3. Прирівняйте кожен вираз у дужках до нуля (як окремі рівняння). так ми знайдемо два значення , при яких все рівняння дорівнює нулю, = 0. Тепер залишається прирівняти до нуля кожне з виразів в дужках. Чому? Справа в тому, що добуток дорівнює нулю тоді, коли хоча б один з множників дорівнює нулю. Так як дорівнює нулю, то або (3x + 1), або (x - 4) дорівнює нулю. Записавши і .
  4. Вирішіть кожне рівняння окремо. у квадратному рівнянні x має два значення. Вирішіть рівняння і запишіть значення x:
    • Вирішіть рівняння 3x + 1 = 0
      • 3x = -1 ..... шляхом віднімання
      • 3x/3 = -1/3 ..... шляхом ділення
      • X = -1/3 ..... після спрощення
    • Вирішіть рівняння x-4 = 0
      • X = 4 ..... шляхом віднімання
    • X = (-1/3, 4)..... можливі значення, тобто x = -1 / 3 або x = 4.
  5. Перевірте x = -1/3, підставивши це значення в (3x + 1)(x - 4) = 0:
    • (3[-1/3] + 1)([-1/3] – 4) ?=? 0 ..... шляхом підстановки
    • (-1 + 1)(-4 1/3) ?=? 0 ..... після спрощення
    • (0)(-4 1/3) = 0 ..... після множення
    • 0 = 0, отже, x = -1/3 – правильна відповідь.
  6. Перевірте x = 4, підставивши це значення в (3x + 1)(x - 4) = 0:
    • (3[4] + 1)([4] – 4) ?=? 0 ..... шляхом підстановки
    • (13)(4 – 4) ?=? 0 ..... після спрощення
    • (13)(0) = 0 ..... після множення
    • 0 = 0, отже, x = 4 – правильна відповідь.
    • Таким чином, обидва рішення є вірними.

Метод2З 3:
Використання формули коренів квадратного рівняння

  1. Об'єднайте всі члени і запишіть з одного боку рівняння. збережіть значення позитивним. Запишіть члени в порядку зменшення ступенів, таким чином член пишеться першим, далі і потім постійна:
    • 4x 2 - 5x - 13 = x 2 -5
    • 4x 2 - x 2 - 5x - 13 +5 = 0
    • 3x 2 - 5x - 8 = 0
  2. Запишіть формулу коренів квадратного рівняння. Формула має наступний вигляд: [2]
  3. Визначте значення a, b і c в квадратному рівнянні. змінна a - коефіцієнт члена x 2 , b - члена x, c - постійна. Для рівняння 3x 2 - 5x - 8 = 0, a = 3, b = -5, і c = -8. Запишіть це.
  4. Підставте значення a, b і c в рівняння. знаючи значення трьох змінних, Ви можете підставити їх в рівняння наступним чином:
    • {-b +/-√ (b 2 - 4ac)}/2
    • {-(-5) +/-√ ((-5) 2 - 4(3)(-8))}/2(3) =
    • {-(-5) +/-√ ((-5) 2 - (-96))}/2(3)
  5. Підрахуйте. підставивши значення, спростіть плюси і мінуси, перемножте або зведіть в квадрат залишилися члени:
    • {-(-5) +/-√ ((-5) 2 - (-96))}/2(3) =
    • {5 +/-√(25 + 96)}/6
    • {5 +/-√(121)}/6
  6. Спростіть квадратний корінь. якщо число під знаком квадратного кореня – квадрат, Ви отримаєте ціле число. Якщо ні, спростіть його до найбільш простого значення кореня. Якщо число негативне, і ви впевнені, що воно повинно бути негативним , то коріння будуть складні. У цьому прикладі √(121) = 11. Можете записати, що x = (5 +/- 11)/6.
  7. Знайдіть позитивні та негативні рішення. якщо ви видалили знак квадратного кореня, то можете продовжувати до тих пір, поки не знайдете позитивні і негативні значення x. маючи (5 +/- 11)/6, можна записати:
    • (5 + 11)/6
    • (5 - 11)/6
  8. Знайдете позитивні і негативні значення. просто порахуйте:
    • (5 + 11)/6 = 16/6
    • (5-11)/6 = -6/6
  9. Спростіть. для цього просто розділіть обидва на найбільший спільний дільник. Першу дріб ділите на 2, другу на 6, x.
    • 16/6 = 8/3
    • -6/6 = -1
    • X = (-1, 8/3)

Метод3З 3:
Доповнення до повного квадрата

  1. Перенесіть всі члени на одну сторону рівняння. a або x 2 повинен бути позитивним. Це робиться так: [3]
    • 2x 2 - 9 = 12x =
    • 2x 2 - 12x - 9 = 0
      • У цьому рівнянні a : 2, b : -12, c : -9.
  2. Перенесіть член c (постійну) на іншу сторону. постійна-це член рівняння, що містить тільки Числове значення, без змінних. Перенесіть її в праву частину:
    • 2x 2 - 12x - 9 = 0
    • 2x 2 - 12x = 9
  3. Розділіть обидві частини на коефіцієнт a або x 2 . якщо x 2 не має коефіцієнта, то він дорівнює одиниці і цей крок можна пропустити. У нашому прикладі всі члени ділимо на 2:
    • 2x 2 /2 - 12x/2 = 9/2 =
    • X 2 - 6x = 9/2
  4. Розділіть b на 2, зведіть в квадрат і додайте до обох сторін. у нашому прикладі b дорівнює -6:
    • -6/2 = -3 =
    • (-3) 2 = 9 =
    • X 2 - 6x + 9 = 9/2 + 9
  5. Спростіть обидві сторони. зведіть в квадрат члени зліва і вийде (x-3) (x-3), або (x-3) 2 . Складіть члени праворуч і вийде 9/2 + 9, або 9/2 + 18/2, що дорівнює 27/2.
  6. Вийміть квадратний корінь з обох частин. квадратний корінь з (x-3) 2 дорівнює просто (x-3). Квадратний корінь з 27/2 можна записати як ±√(27/2). Таким чином, x-3 = ±√(27/2).
  7. Спростіть підкорене виразІ знайдіть x. щоб спростити ±√(27/2), знайдіть повний квадрат у числах 27 і 2 або їх множниках. У 27 є повний квадрат 9, адже 9 x 3 = 27. Щоб вивести 9 з під знака кореня, витягніть з нього корінь і винесіть 3 з-під знака кореня. Залиште 3 в чисельники дробу під знаком кореня, так як цей множник витягти не можна, а також залиште 2 знизу. Далі перенесіть постійну 3 з лівої частини рівняння в праву і запишіть два рішення для x:
    • X = 3 +(√6)/2
    • X = 3 - (√6)/2)

Поради

  • Якщо число під знаком кореня не повний квадрат, то останні кілька кроків виконуються трохи інакше. Ось приклад:
  • Як бачите, знак кореня не зник. Таким образом в чисельники об'єднати не можна. Тоді немає сенсу розбивати плюс-або-мінус. Замість цього ми ділимо будь-які загальні множники-алеТільки якщо множник загальний для постійної І коефіцієнта кореня.



Джерела

  1. ↑ Http://www.mathsisfun.com/algebra/factoring-quadratics.html
  2. ↑ Http://www.purplemath.com/modules/quadform.htm
  3. ↑ Http://www.mathsisfun.com/algebra/completing-square.html

Ще почитати: