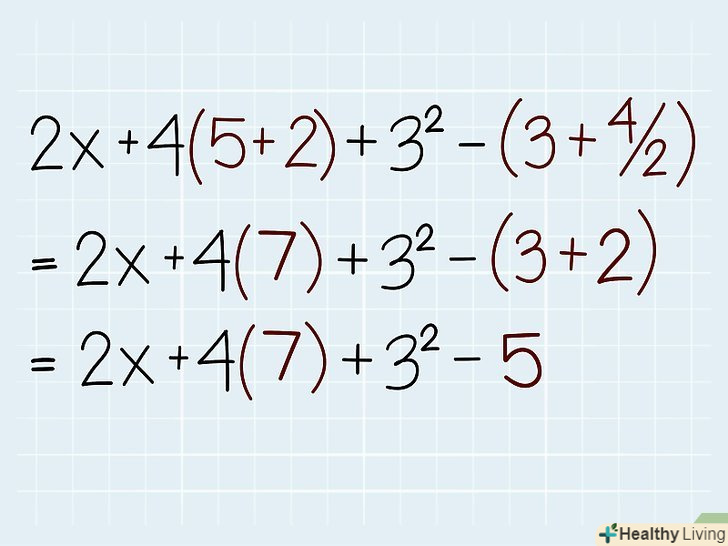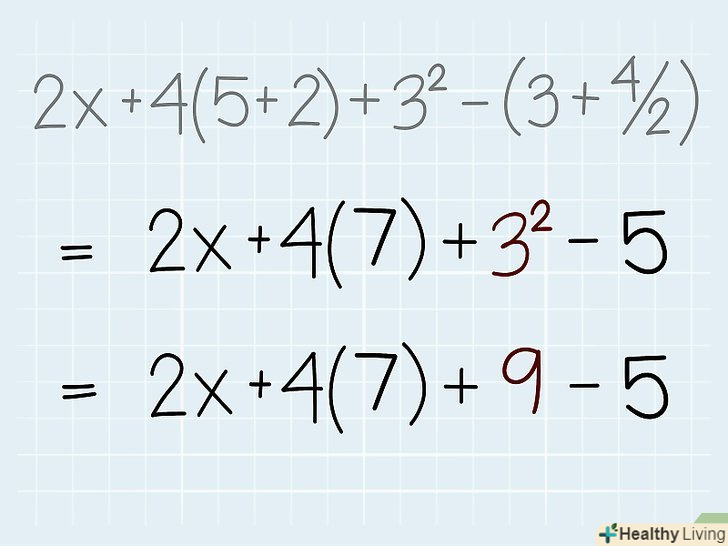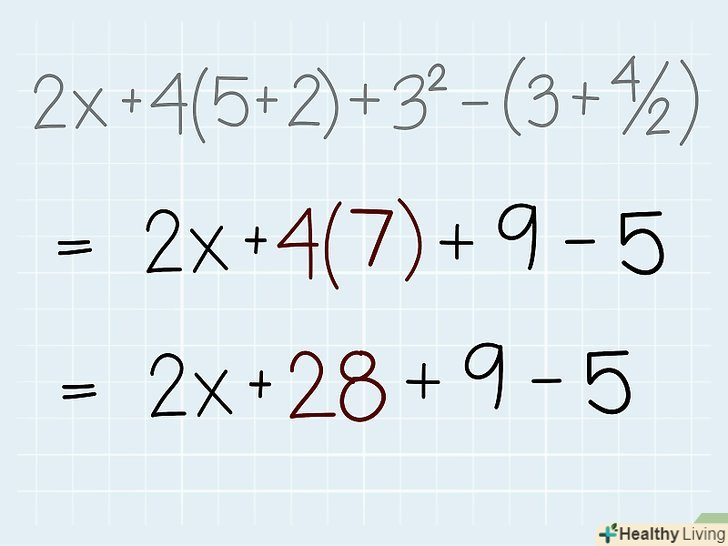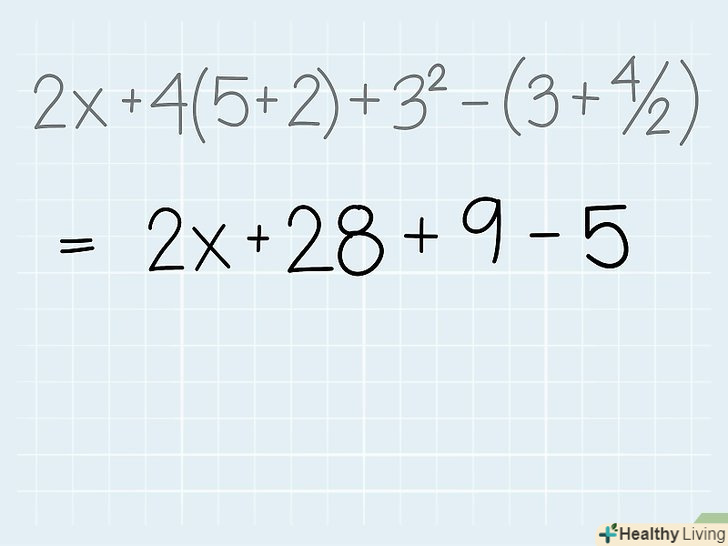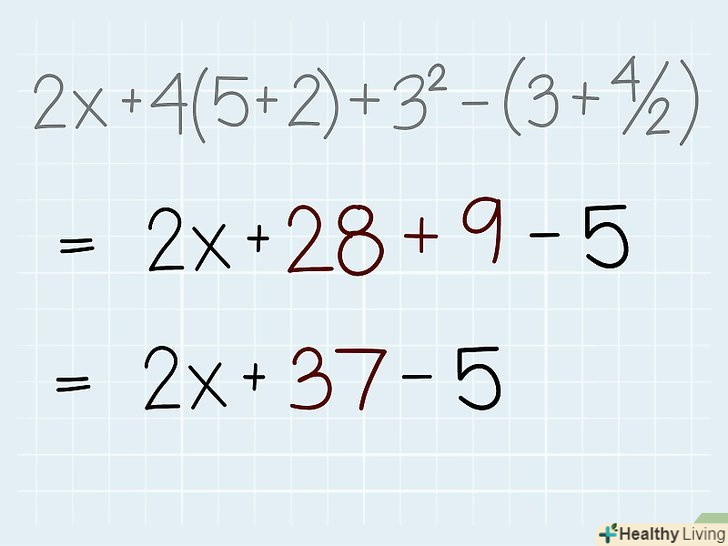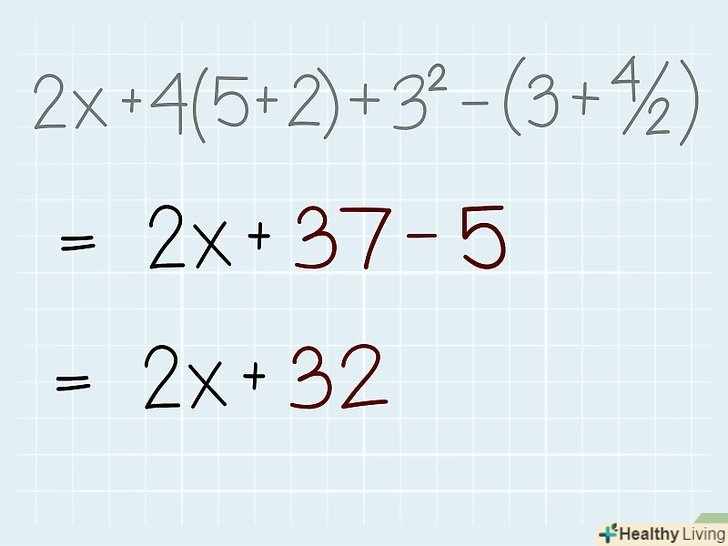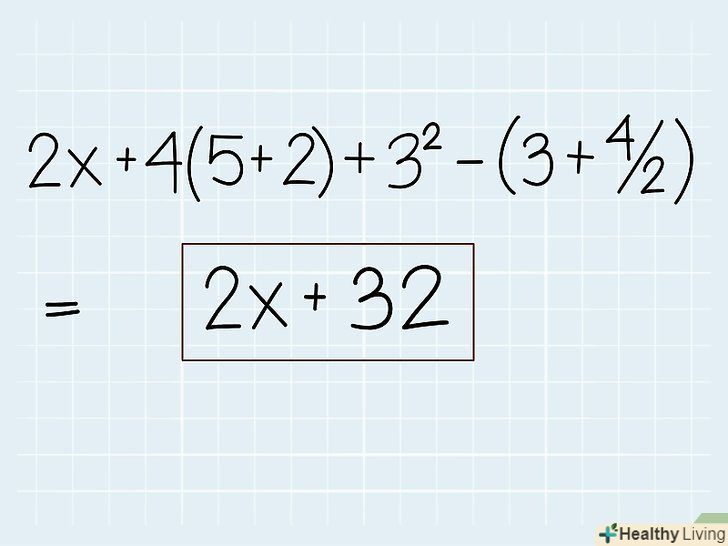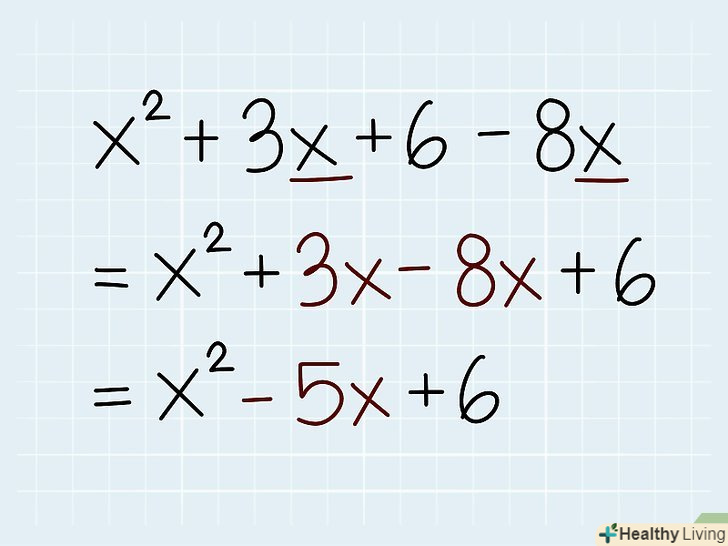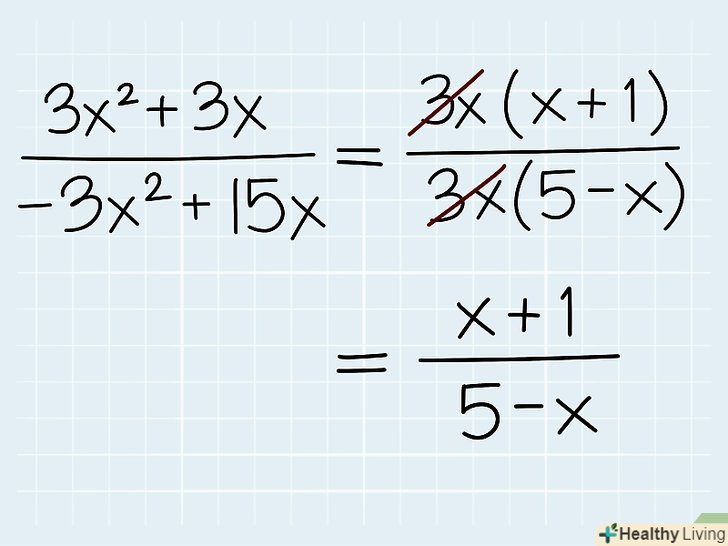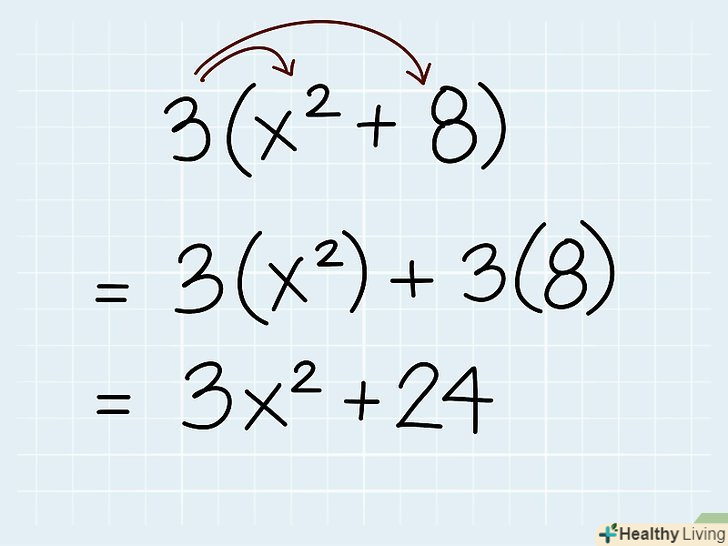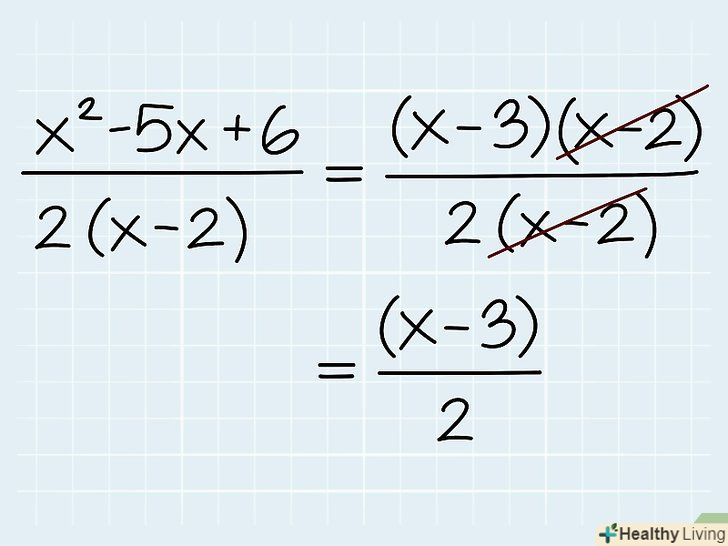1. Головна
    2. Математика
    3. Як спростити математичний вираз: 13 кроків

Як спростити математичний вираз: 13 кроків

Найчастіше в задачах потрібно привести спрощену відповідь. Хоча і спрощені, і не прощені відповіді є вірними, викладач може знизити вашу оцінку, якщо ви не спростите відповідь. Більш того, з спрощеним математичним виразом набагато легше працювати. Тому дуже важливо навчитися спрощувати вирази.

Метод1 З 2:
Правильний порядок виконання математичних операцій

  1. Запам'ятайте правильний порядок виконання математичних операцій.при спрощенні математичного виразу необхідно дотримуватися певного порядку дій, так як деякі математичні операції мають пріоритет над іншими і повинні бути зроблені в першу чергу (насправді недотримання правильного порядку виконання операцій приведе вас до неправильного результату). Запам'ятайте наступний порядок виконання математичних операцій: вираз в дужках, зведення в ступінь, множення, ділення, додавання, віднімання.
    • Зверніть увагу, що знання правильного порядку виконання операцій дозволить вам спростити більшість найпростіших виразів, але для спрощення многочлена (вирази зі змінною) необхідно знати спеціальні прийоми (дивіться наступний розділ).
  2. Почніть з вирішення виразу в дужках. в математиці дужки вказують на те, що укладене в них вираз має бути виконано в першу чергу. Тому при спрощенні будь-якого математичного виразу починайте з рішення виразу, укладеного в дужки (при цьому неважливо, які операції потрібно виконати всередині дужок). Але пам'ятайте, що працюючи з виразом, укладеним в дужки, слід дотримуватися порядку проведення операцій, тобто члени в дужках спочатку перемножуються, діляться, складаються, віднімаються і так далі.
    • Наприклад, спростимо вираз2x + 4(5 + 2) + 32 - (3 + 4/2). Тут почнемо з виразів в дужках: 5 + 2 = 7 і 3 + 4/2 = 3 + 2 =5.
      • Вираз у другій парі дужок спрощується до 5, тому що спочатку потрібно розділити 4/2 (відповідно до правильного порядку виконання операцій). Якщо не дотримуватися цього порядку, то ви отримаєте неправильну відповідь: 3 + 4 = 7 і 7 ÷ 2 = 7/2.
    • Якщо в дужках є ще одна пара дужок, почніть спрощення з рішення виразу у внутрішніх дужках, а потім переходите до рішення виразу в зовнішніх дужках.
  3. Зведіть в ступінь.вирішивши вирази в дужках, перейдіть до зведення в ступінь (пам'ятайте, що у ступеня є показник ступеня і підстава ступеня). Зведіть відповідний вираз (або число) в ступінь і підставте результат в дане вам вираз.
    • У нашому прикладі єдиним виразом (числом) у ступені є 32: 32 = 9. В даному вам виразі замість 32 підставте 9 і ви отримаєте: 2x + 4(7) + 9 - 5.
  4. Помножте.Пам'ятайте, що операція множення може позначатися наступними символами:» х«, » ∙ «або»*". Але якщо між числом і змінною (наприклад, 2х) або між числом і числом в дужках(наприклад, 4 (7)) немає ніяких символів, то це також є операцією множення.
    • У нашому прикладі присутні дві операції множення: 2x(два помножити на змінну «х») і 4 (7) (чотири помножити на сім). Ми не знаємо значення х, тому вираз 2х залишимо як є. 4 (7) = 4 х 7 = 28. Тепер ви можете переписати дане вам вираз так: 2x + 28 + 9 - 5.
  5. Розділіть.Пам'ятайте, що операція ділення може позначатися наступними символами:»/«, » ÷ « або » – " (останній символ ви можете зустріти в дробах). Наприклад 3/4-це три, поділене на чотири.
    • У нашому прикладі операції ділення більше немає, так як Ви вже розділили 4 на 2 (4/2) при вирішенні виразу в дужках. Тому Ви можете перейти до наступного кроку. Пам'ятайте, що в більшості виразів Немає відразу всіх математичних операцій (тільки деякі з них).
  6. Складіть. при додаванні членів виразу ви можете почати з самого крайнього (зліва) члена, або можете спочатку скласти ті члени виразу, які легко складаються. Наприклад, у виразі 49 + 29 + 51 +71 спочатку легше скласти 49 + 51 = 100, потім 29 + 71 = 100 і, нарешті, 100 + 100 = 200. Набагато складніше складати так: 49 + 29 = 78; 78 + 51 = 129; 129 + 71 = 200.
    • У нашому прикладі 2x + 28 + 9 + 5 присутні дві операції складання. Почнемо з самого крайнього (зліва) члена: 2x + 28; ви не можете скласти 2х і 28, тому що не знаєте значення змінної «х». Тому складіть 28 + 9 = 37. Тепер вираз можна переписати так: 2х + 37 - 5.
  7. Відніміть.це остання операція в правильному порядку виконання математичних операцій. На цьому етапі ви також можете додавати негативні числа або ж робити це на етапі складання членів – це ніяк не відіб'ється на кінцевому результаті.
    • У нашому прикладі 2х + 37 - 5 присутній тільки одна операція віднімання: 37 - 5 = 32.
  8. На цьому етапі, виконавши всі математичні операції, ви повинні отримати спрощений вираз.але якщо дане вам вираз містить одну або кілька змінних, то пам'ятайте, що член зі змінною залишиться таким, як є. Рішення (а не спрощення) виразу зі змінною має на увазі знаходження значення цієї змінної. Іноді вирази зі змінною можна спростити, використовуючи спеціальні методи (дивіться наступний розділ).
    • У нашому прикладі остаточну відповідь: 2х + 32. Ви не зможете скласти два члени, поки не дізнаєтеся значення змінної "х". Дізнавшись значення змінної, ви з легкістю спростите цей двучлен.

Метод2 З 2:
Спрощення складних виразів

  1. Додавання подібних членів.Пам'ятайте, що віднімати і складати можна виключно подібні члени, тобто члени з однаковою змінною і однаковим показником ступеня. Наприклад, можна скласти 7x і 5x, але не можна складати 7x і 5x2 (так як тут показники ступеня різні).
    • Це правило поширюється і на Члени з декількома змінними. Наприклад, можна скласти 2xy2 і-3XY2, але не можна складати 2XY2 і-3x2y або 2XY2 і-3y2.
    • Розглянемо приклад: x2 + 3x + 6 - 8x. тут подібними членами є 3X і 8x, тому їх можна скласти. Спрощений вираз виглядає так: x2 - 5x + 6.
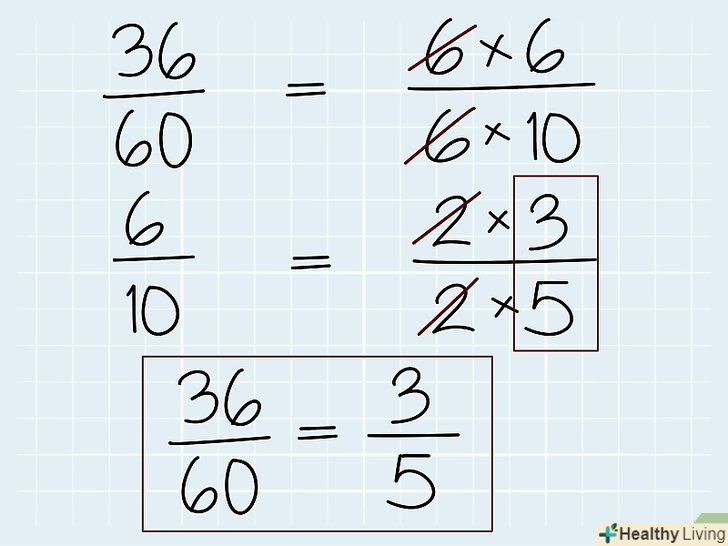
  2. Спростіть числовий дріб.у такому дробі і в чисельнику, і в знаменнику знаходяться числа (без змінної). Числова дріб спрощується декількома способами. По-перше, просто розділіть знаменник на чисельник. По-друге, розкладіть чисельник і знаменник на множники і скоротіть однакові множники (так як при діленні числа на саме себе ви отримаєте 1). Іншими словами, якщо і у чисельника, і у знаменника є один і той же множник, його можна відкинути і отримати спрощену дріб.
    • Наприклад, розглянемо дріб 36/60. За допомогою калькулятора розділіть 36 на 60 і отримаєте 0,6. Але ви можете спростити цей дріб і по-іншому, розклавши чисельник і знаменник на множники: 36/60 = (6х6)/(6х10) = (6/6)*(6/10). Так як 6/6 = 1, то спрощена дріб: 1 х 6/10 = 6/10. Але цей дріб також можна спростити: 6/10 = (2х3)/(2*5) = (2/2)*(3/5) = 3/5.
  3. Якщо дріб містить змінну, можна скоротити однакові множники зі змінною.розкладіть і чисельник, і знаменник на множники і скоротіть однакові множники, навіть якщо вони містять змінну (пам'ятайте, що тут однакові множники можуть містити або не містити змінну).
    • Розглянемо приклад: (3x2 + 3x)/(-3x2 + 15x). Цей вираз можна переписати (розкласти на множники) у вигляді: (x + 1) (3x)/(3x) (5 - x). Так як член 3x знаходиться і в чисельнику, і в знаменнику, його можна скоротити, і ви отримаєте спрощений вираз: (х + 1)/(5 - х). Розглянемо інший приклад: (2x2 + 4x + 6)/2 = (2 (x2 + 2x + 3))/2 = x2 + 2x + 3.
    • Зверніть увагу, що ви не можете скорочувати будь – які члени-скорочуються тільки однакові множники, які присутні як в чисельнику, так і в знаменнику. Наприклад, у виразі(х (х + 2))/х змінна (множник) «х» знаходиться і в чисельнику, і в знаменнику, тому «х» можна скоротити і отримати спрощений вираз: (х + 2)/1 = х + 2. Проте, у виразі (х + 2)/х змінну «х» скорочувати не можна (так як в чисельнику «х» не є множником).
  4. Розкрийте дужки.для цього помножте член, що стоїть за дужкою, на кожен член в дужках. Іноді це допомагає спростити складний вираз. Це стосується як членів, які є простими числами, так і членів, які містять змінну.
    • Наприклад, 3(x2 + 8) = 3x2 + 24, а 3x (x2 + 8) = 3x3 + 24x.
    • Зверніть увагу, що в дробових виразах дужки розкривати не потрібно, якщо і в чисельнику, і в знаменнику присутній однаковий множник. Наприклад, у виразі (3 (x2 + 8)) / 3x дужки розкривати не потрібно, так як тут можна скоротити множник 3 і отримати спрощений вираз (x2 + 8)/x. з цим виразом легше працювати; якби ви розкрили дужки, то отримали б наступне складне вираз: (3x3 + 24x)/3x.
  5. Розкладіть на множники многочлени.за допомогою цього методу можна спростити деякі вирази і многочлени. Розкладання на множники - це операція, протилежна розкриттю дужок, тобто вираз записується у вигляді добутку двох виразів, кожне з яких укладено в дужки. У деяких випадках розкладання на множники дозволяє скоротити однаковий вираз. В особливих випадках (як правило, з квадратними рівняннями) розкладання на множники дозволить вам вирішити рівняння.
    • Розглянемо вираз x2 - 5x + 6. Воно розкладається на множники: (x - 3)(x - 2). Таким чином, якщо, наприклад, дано вираз (x2 - 5x + 6)/(2(x - 2)), то ви можете переписати його у вигляді (x - 3)(x - 2)/(2(x - 2)), скоротити вираз (х - 2) і отримати спрощений вираз (х - 3)/2.
    • Розкладання многочленів на множники застосовується для розв'язання (знаходження коренів) рівнянь (рівняння – це многочлен, прирівняний до 0). Наприклад, розглянемо рівняння x2 - 5x + 6 = 0. Розклавши його на множники, Ви отримаєте (х - 3)(х - 2) = 0. Так як будь - який вираз, помножене на 0, дорівнює 0, то ми можемо записати так: х - 3 = 0 і х-2 = 0. Таким чином, х = 3 і х = 2, тобто Ви знайшли два кореня даного Вам рівняння.

Ще почитати: