Квадратна піраміда-об'ємна фігура з основою у вигляді квадрата і трикутними бічними гранями. Вершина квадратної піраміди проектується в центр підстави. Якщо "а « - сторона квадратного підстави,» h" - висота піраміди (перпендикуляр, опущений з вершини піраміди до центру її підстави), тоді обсяг квадратної піраміди можна обчислити за формулою: a2 x (1/3)h. ця формула вірна для квадратної піраміди будь-яких розмірів (від сувенірних пірамід до єгипетських пірамід).
Кроки
Метод1 З 2:
Обчислення обсягу по площі і висоті
Метод1 З 2:
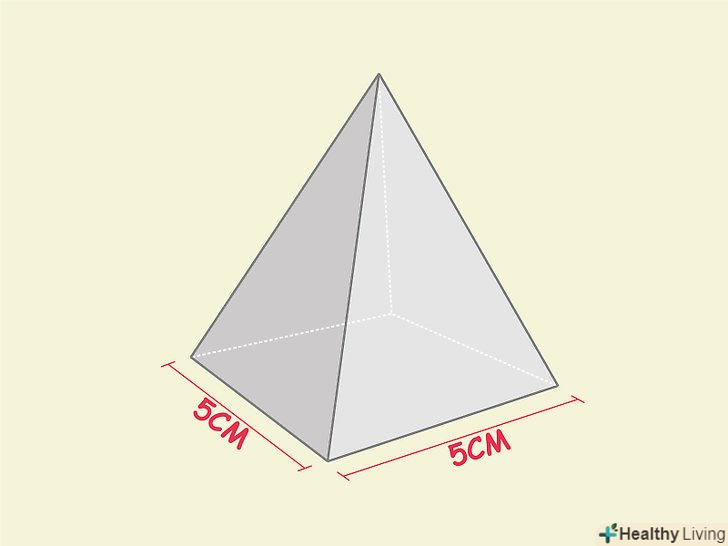
Знайдіть сторону підстави.Так як в підставі квадратної піраміди лежить квадрат, то всі сторони підстави рівні. Тому необхідно знайти довжину будь-якої сторони підстави.- Наприклад, дана піраміда, сторона підстави якої дорівнює 5 см.
- Якщо сторони підстави не рівні один одному, то вам дана прямокутна, а не квадратна піраміда. Тим не менш, формула для обчислення обсягу прямокутної піраміди схожа на формулу для обчислення обсягу квадратної піраміди. Якщо " l " і " w " - дві суміжні (нерівні) сторони прямокутника в основі піраміди, то обсяг піраміди обчислюється за формулою: (l x w) x (1/3)h
-
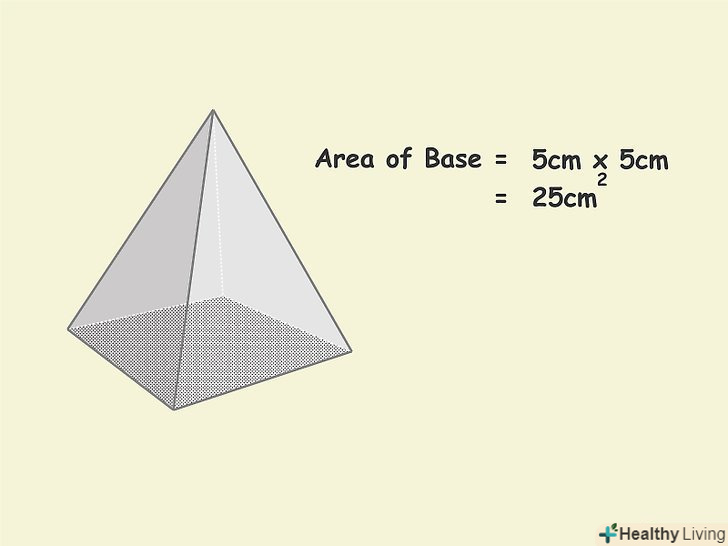
Обчисліть площу квадратного підстави, помноживши його сторону саму на себе (або, іншими словами, звівши сторону в квадрат).
- У нашому прикладі: 5 х 5 = 52 = 25 см2.
- Не забудьте, що площа вимірюється в квадратних одиницях-квадратних сантиметрах, квадратних метрах, квадратних кілометрах і так далі.
-
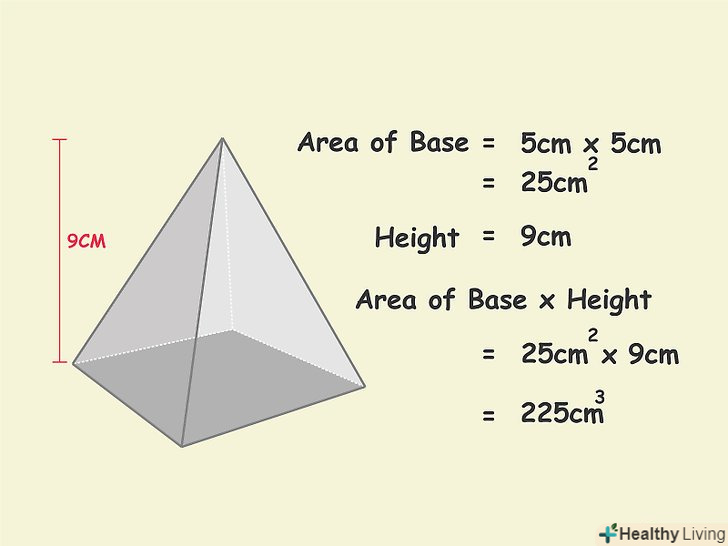
Помножте площу основи на висоту піраміди.висота - перпендикуляр, опущений з вершини піраміди на її підставу. Перемноживши ці величини, ви отримаєте обсяг куба з тим же підставою і висотою, як у піраміди.
- У нашому прикладі висота дорівнює 9 см: 25 см2 x 9 см = 225 см3
- Не забувайте, що обсяг вимірюється в кубічних одиницях, в даному випадку в кубічних сантиметрах.
-
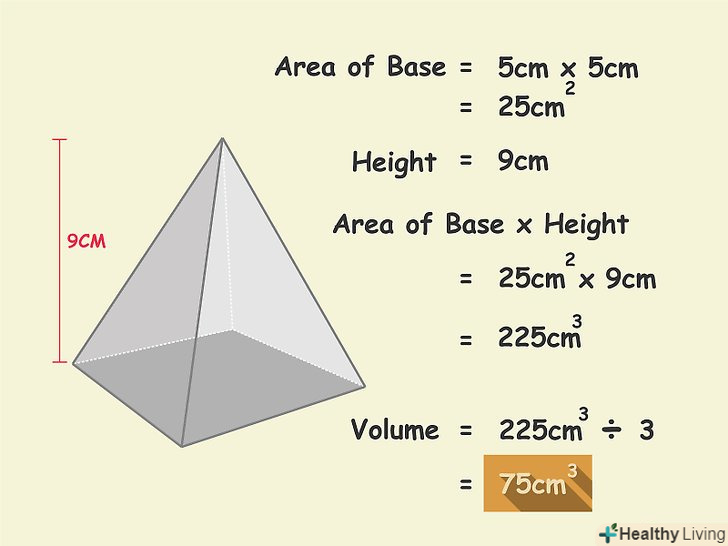
Розділіть отриманий результат на 3 і ви знайдете обсяг квадратної піраміди.
- У нашому прикладі: 225 см3 / 3 = 75 см3.
- Обсяг вимірюється в кубічних одиницях.
Метод2 З 2:
Обчислення обсягу по апофемі
Метод2 З 2:
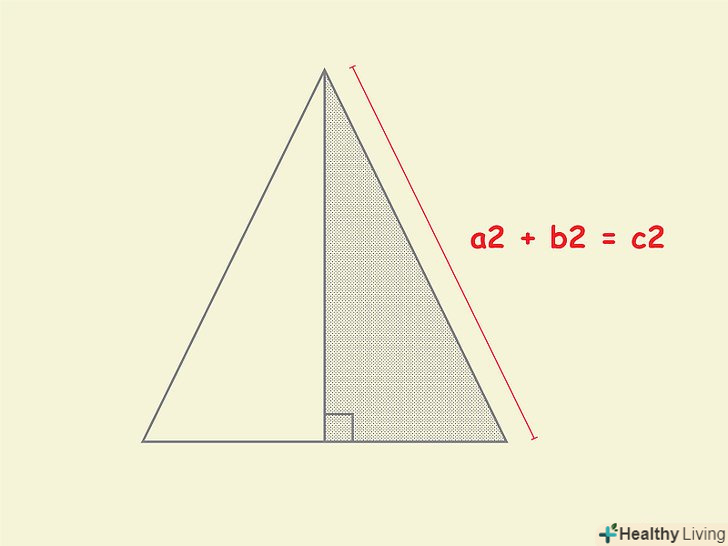
- Якщо вам дано або площу, або висоту піраміди та її апофему, ви можете знайти об'єм піраміди, використовуючи теорему Піфагора.Апофема-це висота похилої трикутної грані піраміди, проведена з вершини трикутника до його основи. Для обчислення апофеми використовуйте сторону підстави піраміди і її висоту.
- Апофема ділить сторону підстави навпіл і перетинає її під прямим кутом.
- Апофема ділить сторону підстави навпіл і перетинає її під прямим кутом.
-
Розгляньте прямокутний трикутник, утворений апофемою, висотою і відрізком, що з'єднує центр підстави і середину його боку.у такому трикутнику апофема є гіпотенузою, яку можна знайти за теоремою Піфагора. Відрізок, що з'єднує центр підстави і середину його боку, дорівнює половині сторони підстави (цей відрізок є одним з катетів; другим катетом є висота піраміди).
- Нагадаємо, що теорема Піфагора записується так: a2 + b2 = c2, де «a» і «b» - катети, «c» - гіпотенуза прямокутного трикутника.
- Наприклад, дана піраміда, у якій сторона підстави дорівнює 4 см, а апофема - 6 см.щоб знайти висоту піраміди, підставте ці значення в теорему Піфагора.
- a2 + b2 = c2
- a2 + (4/2)2 = 62
- a2 = 32
- a = √32 = 5,66 см Ви знайшли другий катет прямокутного трикутника, який є висотою піраміди (аналогічно, якщо була б дана апофема і висота піраміди, ви б могли знайти половину сторони основи піраміди).
-
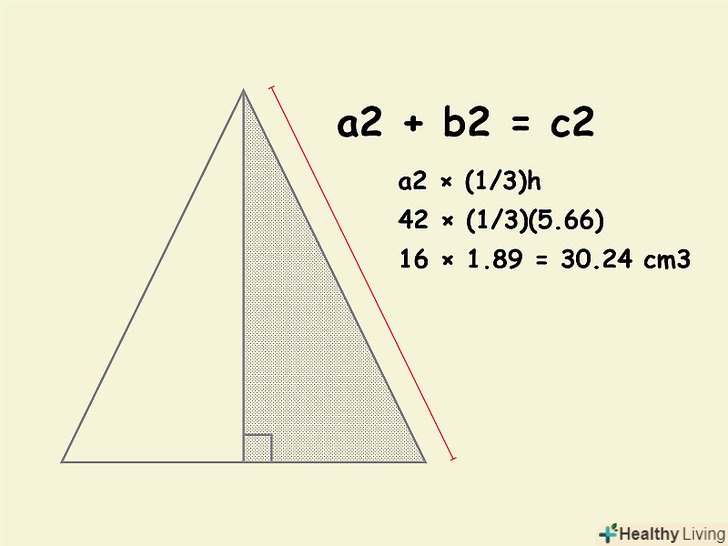
Використовуйте знайдене значення, щоб знайти об'єм піраміди за формулою: a2 x (1/3)h.
- У нашому прикладі ви вирахували, що висота піраміди дорівнює 5,66 см. підставте необхідні значення в формулу для обчислення обсягу піраміди:
- a2 × (1/3)h
- 42 × (1/3)(5,66)
- 16 × 1,89 =30,24 см3.
- У нашому прикладі ви вирахували, що висота піраміди дорівнює 5,66 см. підставте необхідні значення в формулу для обчислення обсягу піраміди:
-
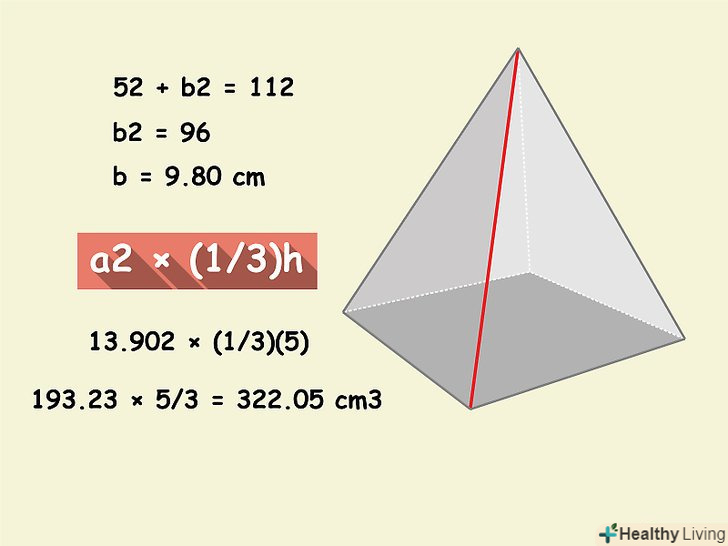
Якщо вам не дана апофема, використовуйте ребро піраміди. Ребро-це відрізок, що з'єднує вершину піраміди з вершиною квадрата в основі піраміди. В цьому випадку ви отримаєте прямокутний трикутник, катетами якого є висота піраміди і половина діагоналі квадрата в підставі піраміди, а гіпотенузою – ребро піраміди. Так як діагональ квадрата дорівнює √2 х сторону квадрата, то ви можете знайти сторону квадрата (підстави), розділивши діагональ на √2. Потім ви зможете знайти обсяг піраміди по вищеописаної формулою.
- Наприклад, дана квадратна піраміда з висотою 5 см і ребром 11 см. обчисліть половину діагоналі наступним чином:
- 52 + b2 = 112
- b2 = 96
- b = 9,80 см.
- Ви знайшли половину діагоналі, тому діагональ дорівнює: 9,80 см х 2 = 19,60 см.
- Сторона квадрата (підстави) дорівнює √2 х діагональ, тому 19,60 / √2 = 13,90 см. тепер знайдіть обсяг піраміди за формулою:A2 x (1/3)h
- 13,902 × (1/3)(5)
- 193,23 × 5/3 =322,05 см3
- Наприклад, дана квадратна піраміда з висотою 5 см і ребром 11 см. обчисліть половину діагоналі наступним чином:
Поради
- У квадратній піраміді її висота, апофема і сторона підстави пов'язані теоремою Піфагора: (сторона ÷ 2)2 + (висота)2 = (апофема)2
- У будь-якій правильній піраміді апофема, сторона основи і ребро пов'язані теоремою Піфагора: (сторона ÷ 2)2 + (апофема)2 = (ребро)2
