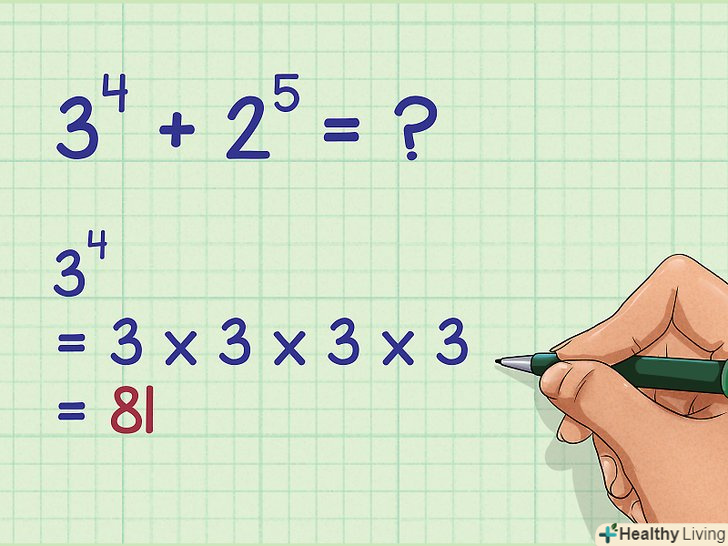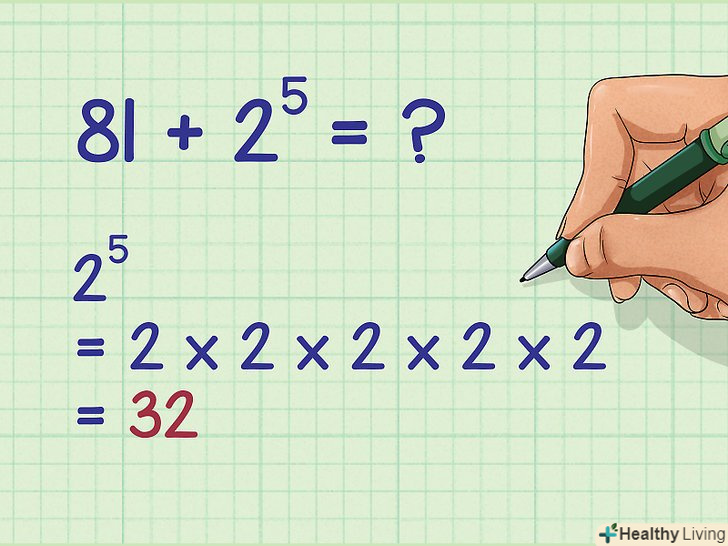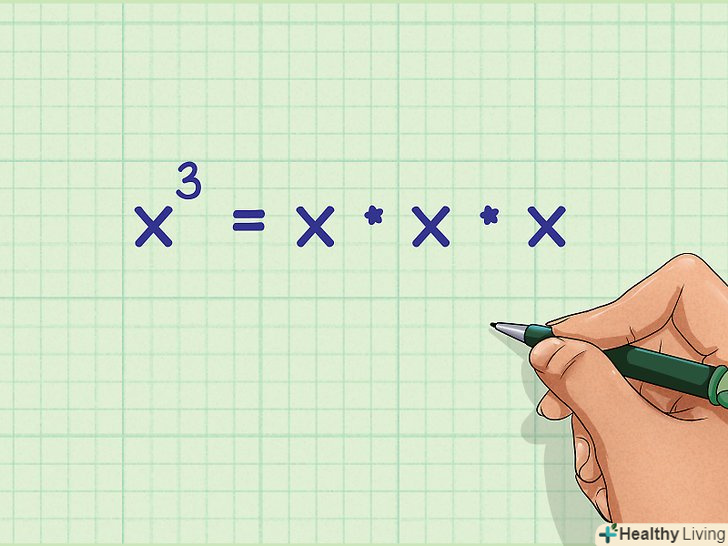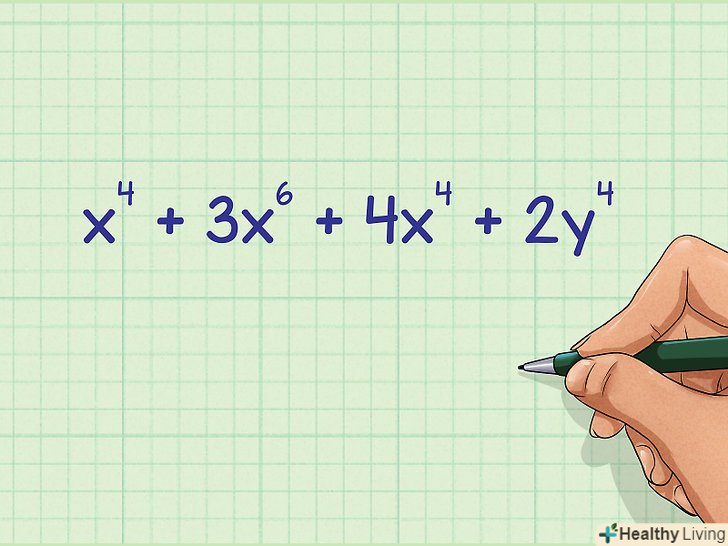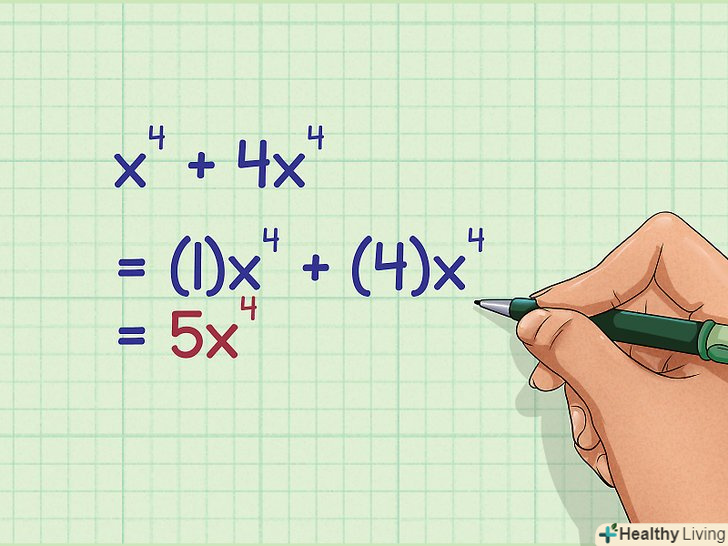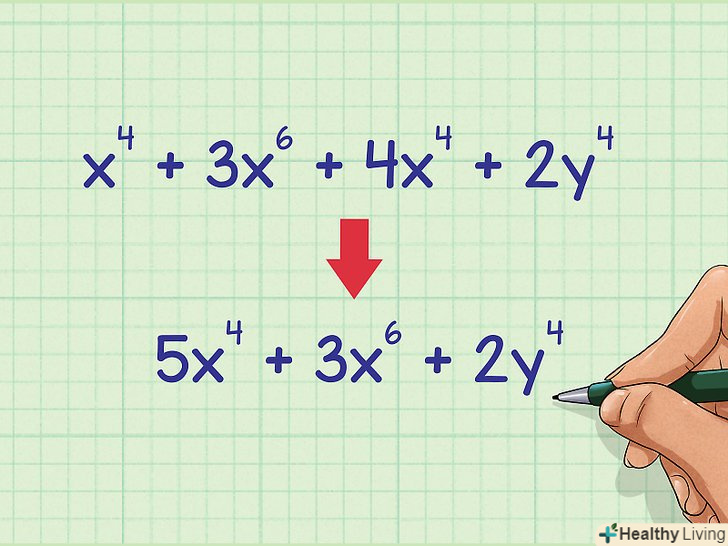Ступінь, а точніше показник ступеня, говорить нам про те, скільки разів слід помножити дане число (підстава ступеня) на саме себе.[1] щоб знайти суму ступенів, слід вміти визначити, вручну або на калькуляторі, значення кожного доданку. При додаванні змінних зі ступенями необхідно знати правила підсумовування схожих членів.
Кроки
Метод1З 3:
Додавання чисел зі ступенями вручну
Метод1З 3:
 Обчисліть перший степеневий вираз.воно складається з підстави (велике число внизу) і показника (менше за розміром число справа вгорі) ступеня. Показник ступеня визначає, скільки разів слід помножити підставу саме на себе (наприклад,
Обчисліть перший степеневий вираз.воно складається з підстави (велике число внизу) і показника (менше за розміром число справа вгорі) ступеня. Показник ступеня визначає, скільки разів слід помножити підставу саме на себе (наприклад,).[2]
- Наприклад, якщо дано вираз
, спочатку слід обчислити
:
- Наприклад, якщо дано вираз
 Обчисліть другий степеневий вираз.для цього помножте підставу ступеня на саме себе стільки разів, скільки вказано в показнику ступеня.
Обчисліть другий степеневий вираз.для цього помножте підставу ступеня на саме себе стільки разів, скільки вказано в показнику ступеня.- Після попередньої дії наш приклад має вигляд
, тому необхідно обчислити
:
- Після попередньої дії наш приклад має вигляд
 Складіть отримані значення.таким чином ви знайдете суму двох статечних виразів.
Складіть отримані значення.таким чином ви знайдете суму двох статечних виразів.- У нашому прикладі:
- У нашому прикладі:
Метод2 З 3:
Додавання чисел зі ступенями на калькуляторі
Метод2 З 3:
 Знайдіть на калькуляторі клавішу ступеня. як правило, на ній написано
Знайдіть на калькуляторі клавішу ступеня. як правило, на ній написано,
або
з порожнім квадратом, який позначає показник ступеня. Даний метод не годиться, якщо у вашому калькуляторі немає опції зведення в ступінь.
 Введіть перший статечний вираз.для цього введіть спочатку підставу ступеня (більше число), а потім показник ступеня.
Введіть перший статечний вираз.для цього введіть спочатку підставу ступеня (більше число), а потім показник ступеня.- Наприклад, якщо дано вираз
, для введення першого доданку слід натиснути наступні клавіші:
- Наприклад, якщо дано вираз
 Натисніть клавішу додавання.в результаті у вас вийде значення першого доданку. Після цього не потрібно натискати знак рівності (клавішу
Натисніть клавішу додавання.в результаті у вас вийде значення першого доданку. Після цього не потрібно натискати знак рівності (клавішу).
- У нашому прикладі після введення виразу
слід натиснути клавішу
, і у вас вийде
.
- У нашому прикладі після введення виразу
 Введіть другий статечний вираз.для цього введіть спочатку підставу ступеня (більше число), а потім показник ступеня.
Введіть другий статечний вираз.для цього введіть спочатку підставу ступеня (більше число), а потім показник ступеня.- Наприклад, якщо дано вираз
, для введення другого доданку слід натиснути такі клавіші:
- Наприклад, якщо дано вираз
 Натисніть знак рівності (клавішу
Натисніть знак рівності (клавішу).в результаті у вас вийде сума двох статечних виразів.
- У нашому прикладі, після того як ви натиснете на необхідні клавіші, ви знайдете, що сума
дорівнює
.
- У нашому прикладі, після того як ви натиснете на необхідні клавіші, ви знайдете, що сума
Метод3 З 3:
Додавання змінних зі ступенями
Метод3 З 3:
 Знайдіть доданки з однаковими підставами і показниками ступеня. підстава має вигляд більшого числа (або змінної) внизу, а показник ступеня стоїть справа вгорі.
Знайдіть доданки з однаковими підставами і показниками ступеня. підстава має вигляд більшого числа (або змінної) внизу, а показник ступеня стоїть справа вгорі. Складіть доданки з однаковими підставами і показниками ступеня.[5] при роботі зі змінними можна складати лише ті члени, у яких однакові підстави і показники ступеня. Тобто однаковими повинні бути обидві ці частини.
Складіть доданки з однаковими підставами і показниками ступеня.[5] при роботі зі змінними можна складати лише ті члени, у яких однакові підстави і показники ступеня. Тобто однаковими повинні бути обидві ці частини.- Наприклад, якщо дано вираз
, то неважко помітити, що доданки
і
мають однакові підстави (
) і показники ступеня (
). Таким чином, ці два члени можна скласти. У доданку
інший показник ступеня, а член
має інша підстава, тому їх не можна складати.
- Наприклад, якщо дано вираз
 Складіть коефіцієнти при схожих членах.Пам'ятайте про те, що при відсутності коефіцієнта він дорівнює
Складіть коефіцієнти при схожих членах.Пам'ятайте про те, що при відсутності коефіцієнта він дорівнює. Не складайте показники ступеня. Показник ступеня повинен залишитися колишнім.
- Наприклад, якщо дано вираз
, слід скласти коефіцієнти перед
, а підставу і показник ступеня залишити тими ж:
- Наприклад, якщо дано вираз
 Запишіть остаточний спрощений вираз.Пам'ятайте про те, що складати слід лише коефіцієнти при членах з однаковою підставою і показником ступеня, причому підстава і показник залишаться колишніми.
Запишіть остаточний спрощений вираз.Пам'ятайте про те, що складати слід лише коефіцієнти при членах з однаковою підставою і показником ступеня, причому підстава і показник залишаться колишніми.- У нашому прикладі вираз
спрощується до
.
- У нашому прикладі вираз
Що вам знадобиться
- олівець
- аркуш паперу
- Калькулятор
Схожі статті
- Як спрощувати алгебраїчні вирази
- Як вирішувати завдання зі ступенями
- Як знайти квадратний корінь числа вручну
- Як використовувати логарифмічні таблиці
- Як обчислити кубічний корінь вручну
- Як зводити в квадрат дробу
- Як спростити квадратний корінь
- Як витягти квадратний корінь без калькулятора
- Як знайти значення числа 10, зведеного в будь-яку цілу ступінь