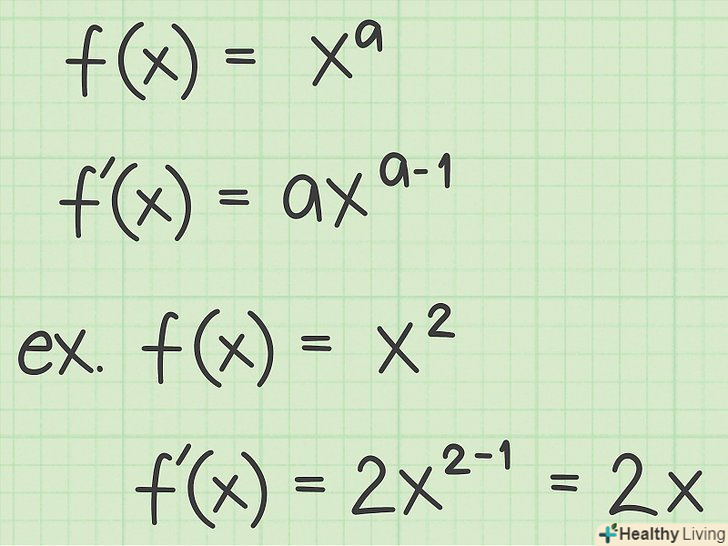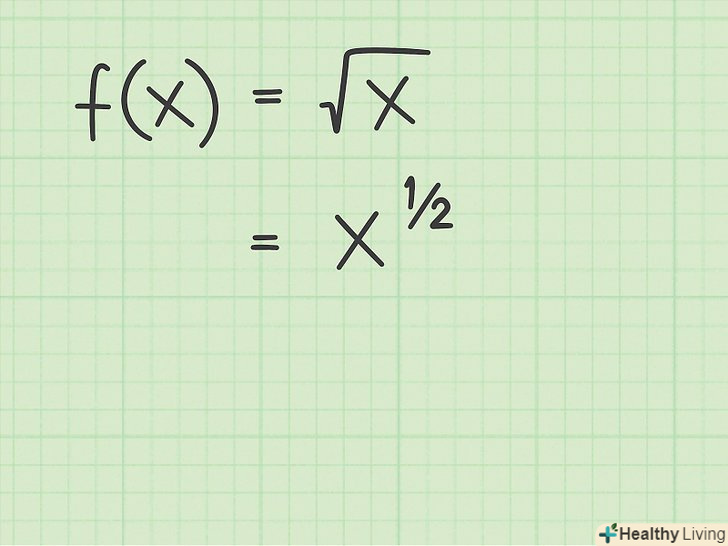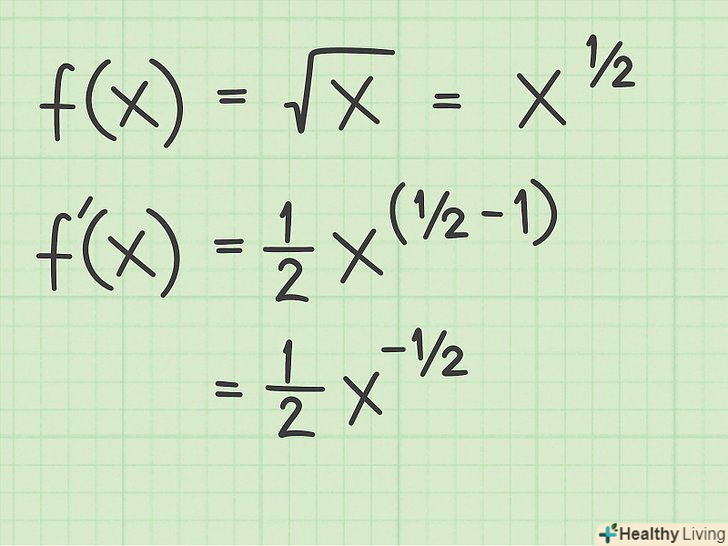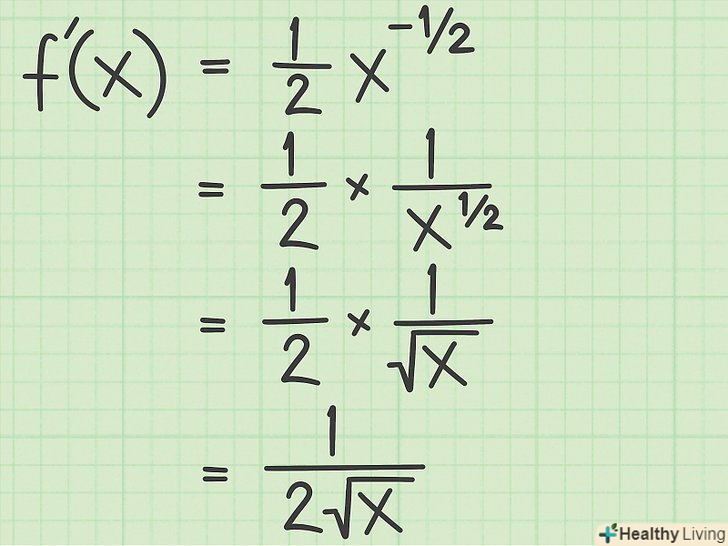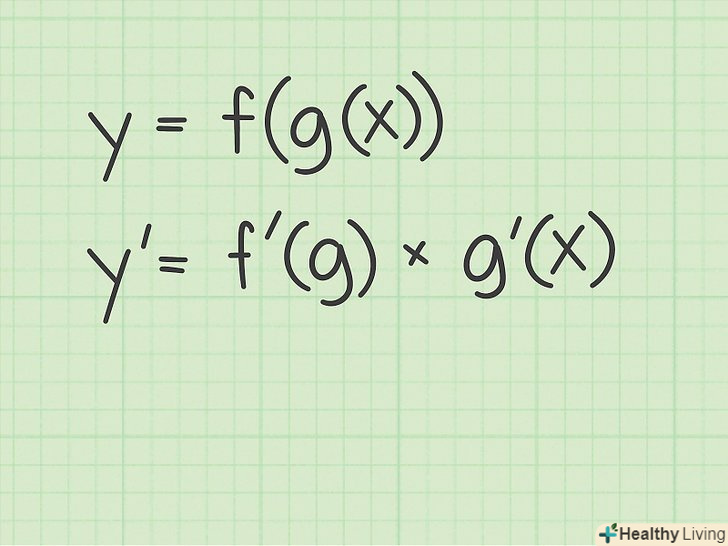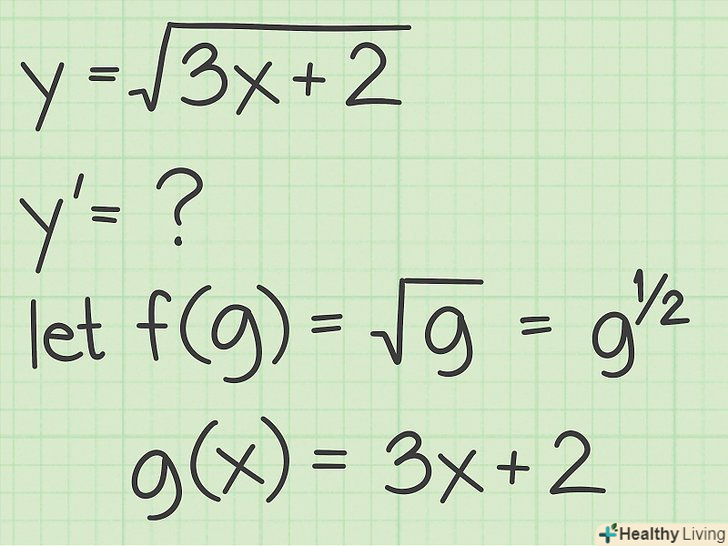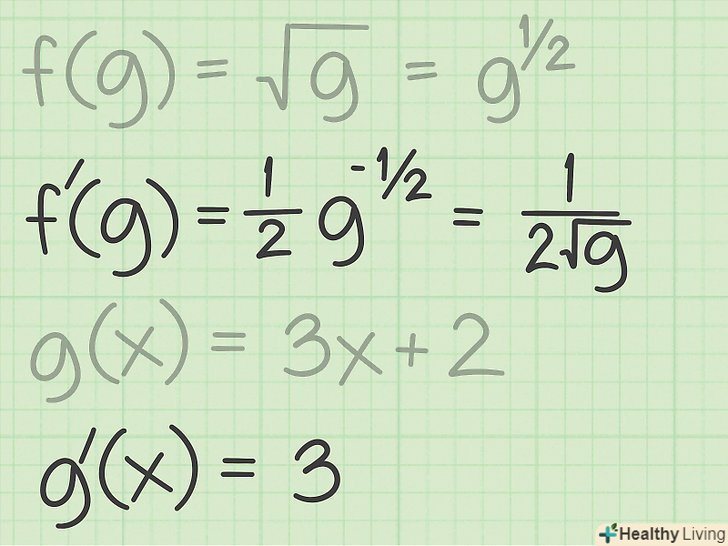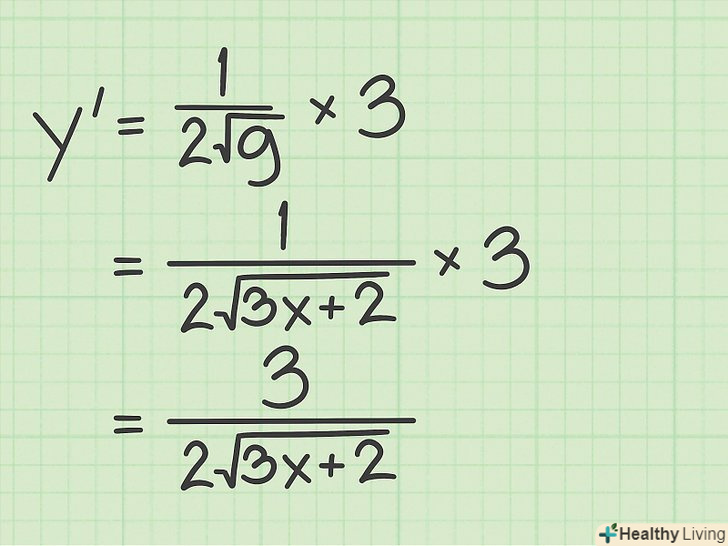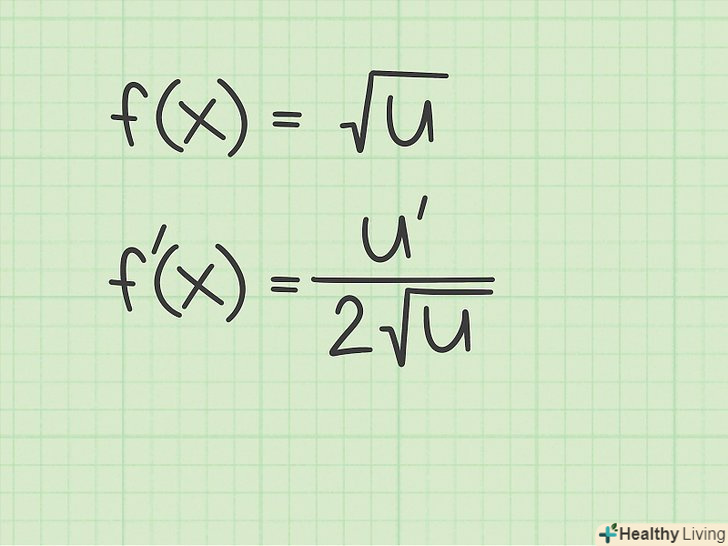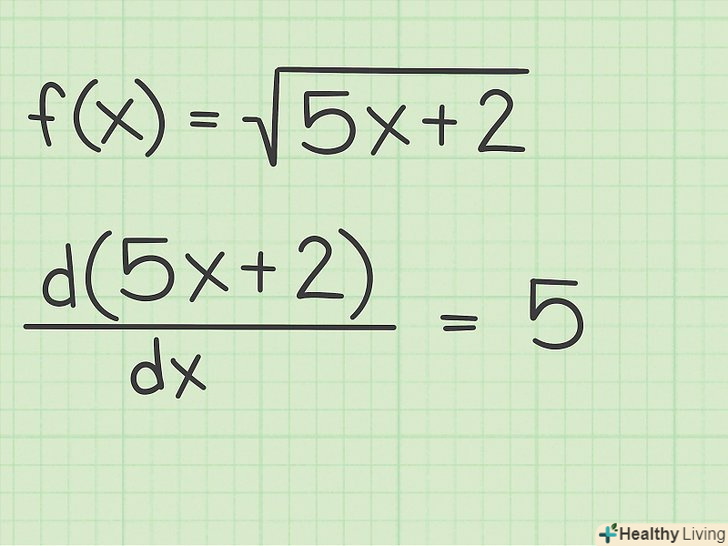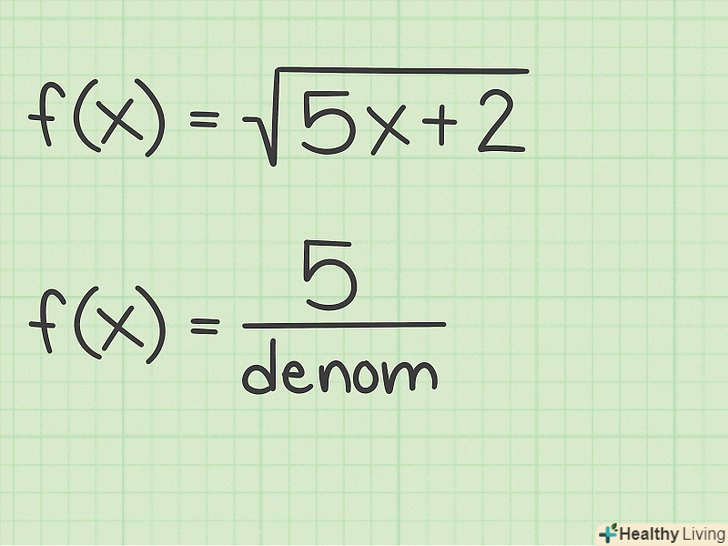На курсах диференціального числення ви напевно вчили правила диференціювання основних функцій, в тому числі правило диференціювання статечної функції. Однак якщо функція містить квадратний або інший корінь, наприклад, може здатися, що дане правило не підходить. Проте досить переписати її в статечному вигляді, щоб отримати очевидну відповідь. Якщо функція містить кілька коренів, таку підстановку можна робити скільки завгодно раз і використовувати правило диференціювання складної функції.
Кроки
Метод1З 3:
За допомогою правила диференціювання статечної функції
Метод1З 3:
 Згадайте правило диференціювання статечної функції.зазвичай це правило вчать на самому початку курсу диференціального числення. Воно свідчить, що похідна змінної
Згадайте правило диференціювання статечної функції.зазвичай це правило вчать на самому початку курсу диференціального числення. Воно свідчить, що похідна змінної, зведена у ступінь
, дорівнює:[1]
- Як приклад розглянемо наступні функції і знайдемо їх похідні:
- Якщо
, то
;
- Якщо
, то
;
- Якщо
, то
;
- Якщо
, то
.
- Якщо
 Запишіть квадратний корінь у вигляді статечної функції.щоб знайти похідну квадратного кореня, згадайте, що його можна переписати у вигляді статечної функції. При цьому стоїть під коренем величина записується у вигляді підстави, яке зводиться в ступінь 1/2. Розглянемо наступні приклади:[2]
Запишіть квадратний корінь у вигляді статечної функції.щоб знайти похідну квадратного кореня, згадайте, що його можна переписати у вигляді статечної функції. При цьому стоїть під коренем величина записується у вигляді підстави, яке зводиться в ступінь 1/2. Розглянемо наступні приклади:[2];
;
.
 Застосуйте правило диференціювання статечної функції. якщо під коренем стоїть змінна x,
Застосуйте правило диференціювання статечної функції. якщо під коренем стоїть змінна x,, похідна береться наступним чином:[3]
(записуємо первісну функцію);
(переписуємо корінь у вигляді статечної функції);
(знаходимо похідну за допомогою правила диференціювання степеневих функцій);
(спрощуємо ступеневу функцію).
 Спростіть результат.на цьому етапі необхідно згадати, що при негативному ступені слід знайти число, зворотне даному числу в тій же позитивній мірі. Ступінь
Спростіть результат.на цьому етапі необхідно згадати, що при негативному ступені слід знайти число, зворотне даному числу в тій же позитивній мірі. Ступіньозначає, що квадратний корінь слід поставити в знаменнику дробу.[4]
- Продовжимо наведений вище приклад для квадратного кореня x і спростимо похідну:
;
;
.
- Продовжимо наведений вище приклад для квадратного кореня x і спростимо похідну:
Метод2 З 3:
За допомогою правила диференціювання складної функції
Метод2 З 3:
 Згадайте правило диференціювання складних функцій.це правило застосовується в тих випадках, коли необхідно продифференцировать функцію, аргументом якої виступає інша функція. Згідно з цим правилом, комбінація двох функцій,
Згадайте правило диференціювання складних функцій.це правило застосовується в тих випадках, коли необхідно продифференцировать функцію, аргументом якої виступає інша функція. Згідно з цим правилом, комбінація двох функцій,і
, диференціюється наступним чином:[5]
- Якщо
, тоді
.
- Якщо
 Визначте функції.при використанні правила диференціювання складних функцій насамперед слід виявити комбінацію функцій. У випадку квадратного кореня в ролі зовнішньої функції
Визначте функції.при використанні правила диференціювання складних функцій насамперед слід виявити комбінацію функцій. У випадку квадратного кореня в ролі зовнішньої функціївиступає взяття кореня, а внутрішньою функцією
є те, що стоїть під знаком кореня.[6]
- Припустимо, необхідно знайти похідну функції
. Визначимо складові її функції наступним чином:
;
.
- Припустимо, необхідно знайти похідну функції
 Знайдіть похідні обох функцій. щоб застосувати правило диференціювання складних функцій до квадратного кореня, спочатку слід знайти похідну квадратного кореня:[7]
Знайдіть похідні обох функцій. щоб застосувати правило диференціювання складних функцій до квадратного кореня, спочатку слід знайти похідну квадратного кореня:[7];
;
.
- Після цього знаходимо похідну другої функції:
;
.
 Комбінуємо знайдені похідні згідно з правилом диференціювання складних функцій. згадуємо це правило (
Комбінуємо знайдені похідні згідно з правилом диференціювання складних функцій. згадуємо це правило () і в результаті отримуємо:[8]
;
;
.
Метод3 З 3:
За допомогою спрощеного правила диференціювання кореня
Метод3 З 3:
 Запам'ятайте просте правило диференціювання будь-яких квадратних коренів.якщо необхідно знайти похідну квадратного кореня, під яким стоїть змінна або функція, використовуйте наступне правило. Результат завжди буде являти собою похідну підкореного виразу, поділену на подвоєний початковий квадратний корінь. Це можна записати наступним чином:[9]
Запам'ятайте просте правило диференціювання будь-яких квадратних коренів.якщо необхідно знайти похідну квадратного кореня, під яким стоїть змінна або функція, використовуйте наступне правило. Результат завжди буде являти собою похідну підкореного виразу, поділену на подвоєний початковий квадратний корінь. Це можна записати наступним чином:[9]- Якщо
, тоді
.
- Якщо
 Знайдіть похідну підкореного виразу.як випливає з назви, підкорене вираз стоїть під знаком квадратного кореня. Щоб застосувати дане правило, знайдемо похідну цього виразу. Розглянемо наступні приклади:[10]
Знайдіть похідну підкореного виразу.як випливає з назви, підкорене вираз стоїть під знаком квадратного кореня. Щоб застосувати дане правило, знайдемо похідну цього виразу. Розглянемо наступні приклади:[10]- У функції
подкоренным виразом є
, а його похідна
;
- У функції
підкореним виразом є
, а його похідна
;
- У функції
підкореним виразом є
, а його похідна
.
- У функції
 Запишіть похідну підкореного виразу в чисельнику дробу.похідна кореня являє собою дріб, в чисельнику якої стоїть похідна підкореного виразу. Для наведених вище функцій отримуємо наступні вирази:[11]
Запишіть похідну підкореного виразу в чисельнику дробу.похідна кореня являє собою дріб, в чисельнику якої стоїть похідна підкореного виразу. Для наведених вище функцій отримуємо наступні вирази:[11]- Якщо
, тоді
- Якщо