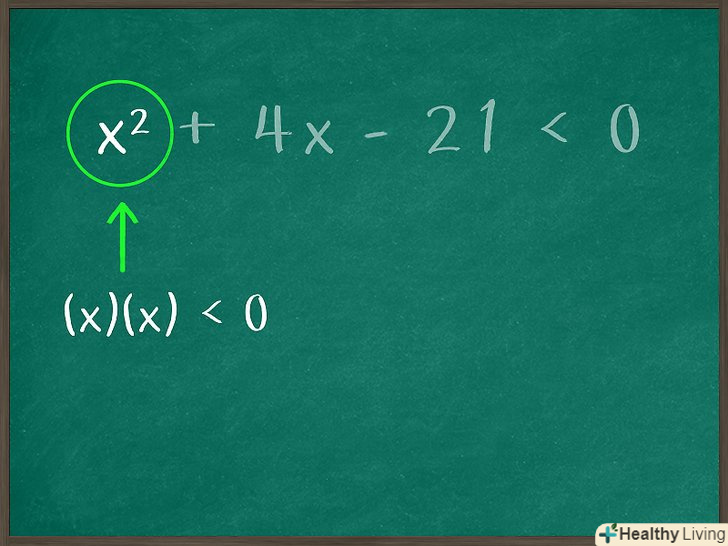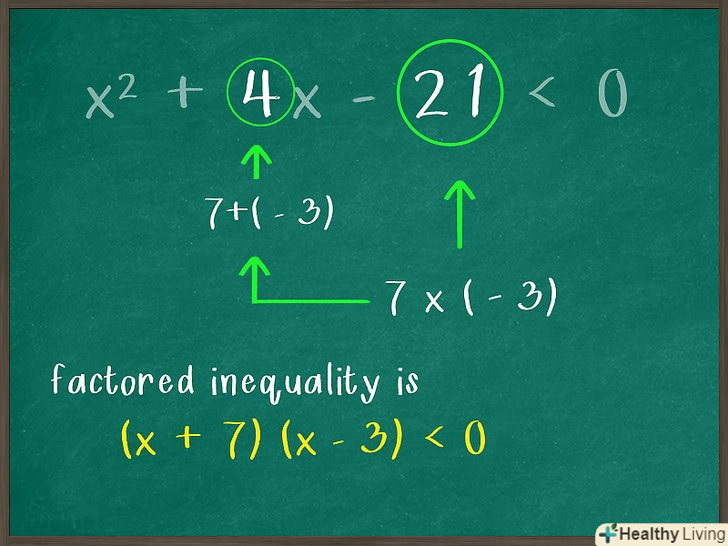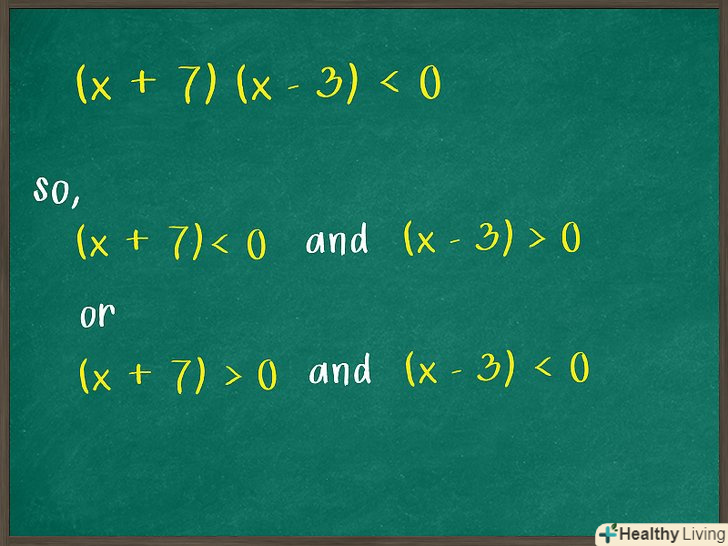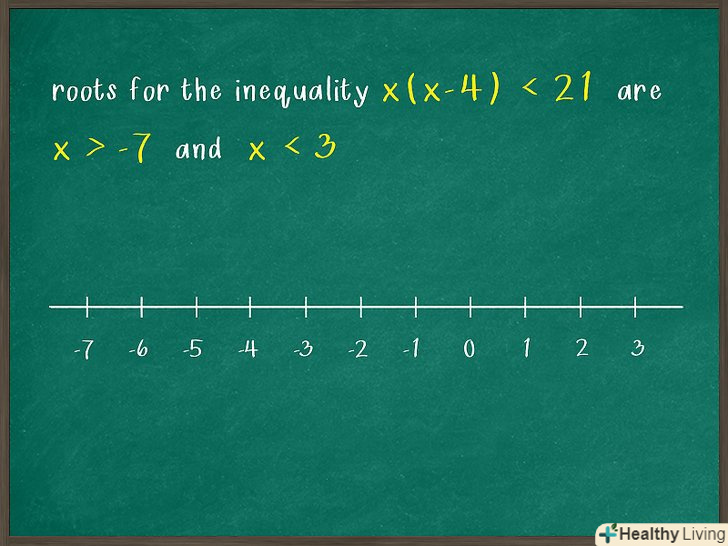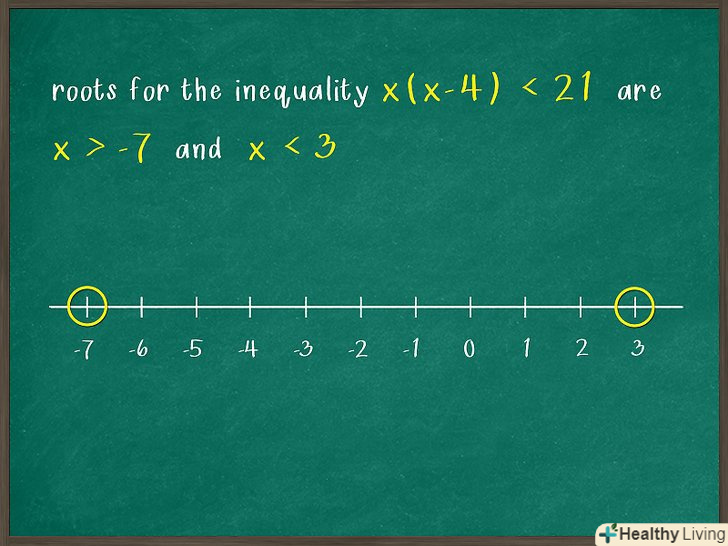Як вирішувати квадратні нерівності (з ілюстраціями)

Квадратна нерівність – це нерівність, в якій змінна зводиться в квадрат ( $x^{2}$ ) і має два кореня. Графік такої нерівності являє собою параболу і перетинає вісь Х в двох точках. Рішення нерівності передбачає знаходження таких значень $x$ , при яких нерівність вірно. Коріння нерівності можна записати в алгебраїчній формі, а також відобразити їх на числовій прямій або координатній площині.

Частина1З 4:

Розкладання нерівності на множники

Запишіть нерівність у стандартній формі.стандартна форма квадратної нерівності являє собою наступний тричлен: $ax^{2}+bx+c&#lt;0$ , де $a$ , $b$ , $c$ – коефіцієнти, і $a\neq 0$ .^{[1]X
Джерело інформації}
- Наприклад, нерівність $x(x+4)&#lt;21$ записано в нестандартній формі. Для початку за допомогою властивості дистрибутивності розкрийте дужки, тобто перемножте $x$ і $x+4$ . Потім відніміть 21 з обох сторін нерівності:
  $x(x+4)&#lt;21$
  $x^{2}+4x&#lt;21$
  $x^{2}+4x-21&#lt;21-21$
  $x^{2}+4x-21&#lt;0$
Знайдіть два одночлена, при перемноженні яких вийде перший член нерівності. щоб вирішити нерівність, потрібно розкласти його на два біноми (двучлена), при перемноженні яких вийде вихідне нерівність, записане в стандартній формі. Біном - це вираз з двома одночленами.^{[2]X
Джерело інформації} Пам'ятайте, що біноми перемножуються за певним правилом. Для початку знайдіть два одночлена, кожен з яких є першим одночленом відповідного бінома.
- Наприклад, $x\times x=x^{2}$ , тому операцію множення двох біномів можна записати так: $(x)(x)&#lt;0$ .
Знайдіть два числа, при перемноженні яких вийде третій член нерівності, записаного в стандартній формі.при цьому сума таких чисел повинна дорівнювати коефіцієнту при другому члені нерівності. Швидше за все, тут числа потрібно шукати методом проб і помилок, щоб вони задовольняли відразу двом описаним умовам. Зверніть увагу на знак («плюс» або «мінус»), який стоїть перед третім членом нерівності.

Наприклад:

$x^{2}+4x-21&#lt;0$

Третій член нерівності дорівнює -21, тому його можна розкласти на множники 7 і -3. Тепер перевірте, чи дорівнює сума цих чисел коефіцієнту ( $4$ ) при другому члені нерівності.

Оскільки $7+(-3)=4$ , ці множники відповідають обом критеріям. Таким чином, вихідне нерівність розкладається на наступні биномы: $(x+7)(x-3)&#lt;0$ .

Частина2З 4:

Знаходження коренів нерівності

Визначте, чи мають обидва біноми однакові знаки. якщо твір біномів більше нуля, то обидва бінома будуть або негативними (менше 0), або позитивними (більше 0), тому що мінус на мінус дає плюс, і плюс на плюс теж дає плюс.^{[3]X
Джерело інформації}
- Якщо нерівність більша або дорівнює нулю ( $\geq$ ) або менше або дорівнює нулю ( $\leq$ ), один або обидва бінома можуть бути рівними нулю.
- Наприклад, у випадку нерівності $(x+7)(x-3)&#lt;0$ твір біномів менше 0, тому біноми не мають однакових знаків.
Визначте, чи мають обидва біноми різні (протилежні) знаки. якщо твір біномів менше нуля, то один Біном буде негативним (менше 0), а другий буде позитивним (більше 0), тому що мінус на плюс дає мінус.
- Якщо нерівність більша або дорівнює нулю ( $\geq$ ) або менше або дорівнює нулю ( $\leq$ ), один або обидва бінома можуть бути рівними нулю.
- Наприклад, у випадку нерівності $(x+7)(x-3)&#lt;0$ твір біномів менше 0, тому біноми мають різні знаки.
Запишіть варіанти з двох нерівностей, щоб знайти коріння вихідної нерівності.для цього кожен Біном перетворите в нерівність, враховуючи той факт, що обидва біноми мають однакові або різні знаки.^{[4]X
Джерело інформації}
- Наприклад, ви визначили, що біноми нерівності $(x+7)(x-3)&#lt;0$ мають різні знаки, тому запишіть два варіанти з двох нерівностей наступним чином:
  $x+7&#lt;0$ І $x-3&#gt;0$ (тобто перший біном буде негативним, а другий – позитивний.)
  або
  $x+7&#gt;0$ І $x-3&#lt;0$ (тобто перший біном буде позитивним, а другий – негативним.)
Вирішіть дві нерівності першого варіанту. для цього ізолюйте змінну $x$ в кожному нерівність. Пам'ятайте, що якщо помножити або розділити обидві сторони нерівності на негативне число, знак нерівності змінюється на протилежний.^{[5]X
Джерело інформації}
- Наприклад, два нерівності першого варіанту: $x+7&#lt;0$ І $x-3&#gt;0$
  - Спочатку вирішіть нерівність $x+7&#lt;0$ (тобто знайдіть $x$ ):
    $x+7-7&#lt;0-7$
    $x&#lt;-7$
  - Потім вирішіть нерівність $x-3&#gt;0$ (тобто знайдіть $x$ ):
    $x-3+3&#gt;0+3$
    $x&#lt;3$
- Таким чином, перша пара коренів вихідної нерівності: $x&#lt;-7$ і $x&#gt;3$
Перевірте дійсність першої пари коренів. для цього знайдіть значення $x$ , що задовольняють обом знайдених коренів. Якщо такі значення існують, коріння дійсні; в іншому випадку корінням можна знехтувати.^{[6]X
Джерело інформації}
- Наприклад, перша пара коренів нерівності: $x&#lt;-7$ і $x&#gt;3$ . Потрібно знайти значення $x$ , що задовольняють обом коріння. Запитайте себе, чи є число, менше -7 і більше 3? Такого числа немає, тому першою парою коренів можна знехтувати.
Вирішіть дві нерівності другого варіанту. для цього ізолюйте змінну $x$ в кожному нерівність. Пам'ятайте, що якщо помножити або розділити обидві сторони нерівності на негативне число, знак нерівності змінюється на протилежний.^{[7]X
Джерело інформації}
- Наприклад, два нерівності другого варіанту: $x+7&#gt;0$ І $x-3&#lt;0$
  - Спочатку вирішіть нерівність $x+7&#gt;0$ (тобто знайдіть $x$ ):
    $x+7-7&#gt;0-7$
    $x&#gt;-7$
  - Потім вирішіть нерівність $x-3&#lt;0$ (тобто знайдіть $x$ ):
    $x-3+3&#lt;0+3$
    $x&#lt;3$
- Таким чином, друга пара коренів вихідної нерівності: $x&#gt;-7$ і $x&#lt;3$
Перевірте дійсність другої пари коренів. для цього знайдіть значення $x$ , що задовольняють обом знайдених коренів. Якщо такі значення існують, коріння дійсні; в іншому випадку корінням можна знехтувати.^{[8]X
Джерело інформації}
- Наприклад, друга пара коренів нерівності: $x&#gt;-7$ і $x&#lt;3$ . Потрібно знайти значення $x$ , що задовольняють обом коріння. Запитайте себе, чи є число (а), більше -7 і менше 3? Таких чисел кілька (наприклад, 0), тому знайдені корені дійсні і є вирішенням вихідної нерівності.

Частина3З 4:

Відображення коренів нерівності на числовій прямій

Намалюйте числову пряму.зробіть це так, як потрібно (в завданні або викладачем). Якщо конкретних вимог немає, під числової прямої напишіть числа, відповідні знайденим раніше коріння (значенням $x$ ). Також можна написати кілька чисел, які більше або менше знайдених значень; так вам буде простіше працювати з числовою прямою.
- Наприклад, корінням нерівності $x(x+4)&#lt;21$ є $x&#gt;-7$ і $x&#lt;3$ . Під числової прямої напишіть числа -7 і 3.
На числовій прямій намалюйте гуртки, що позначають знайдені значення