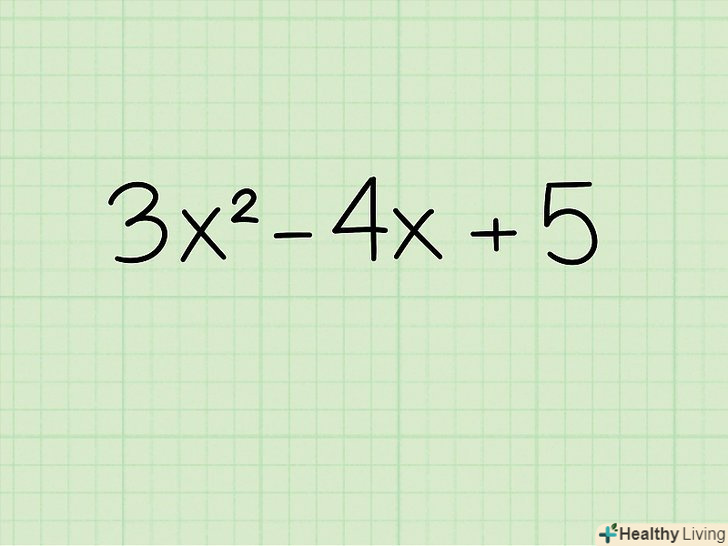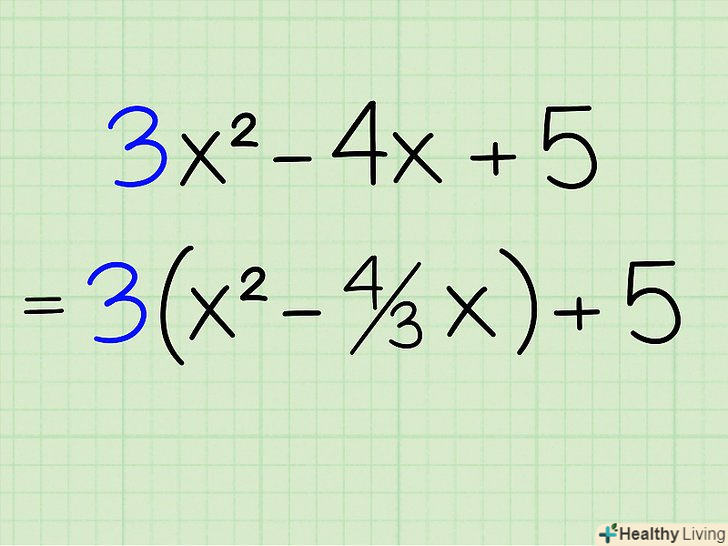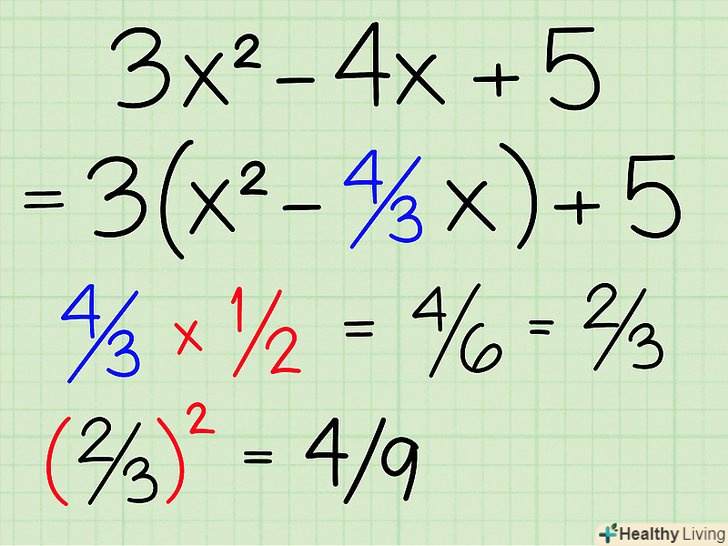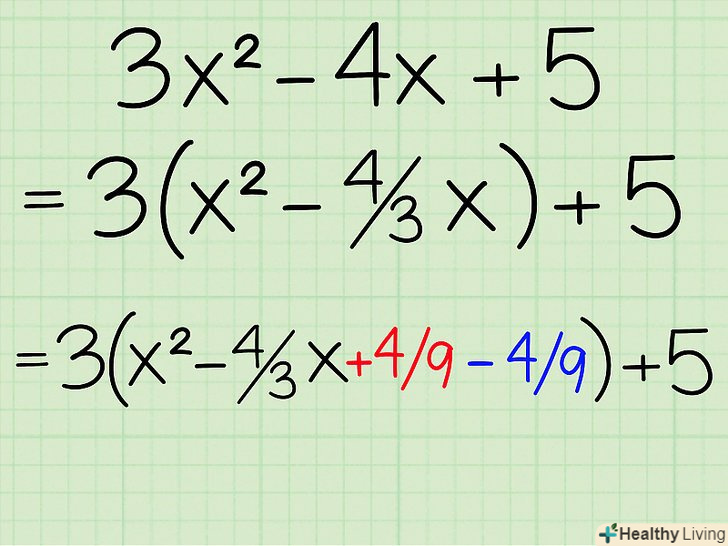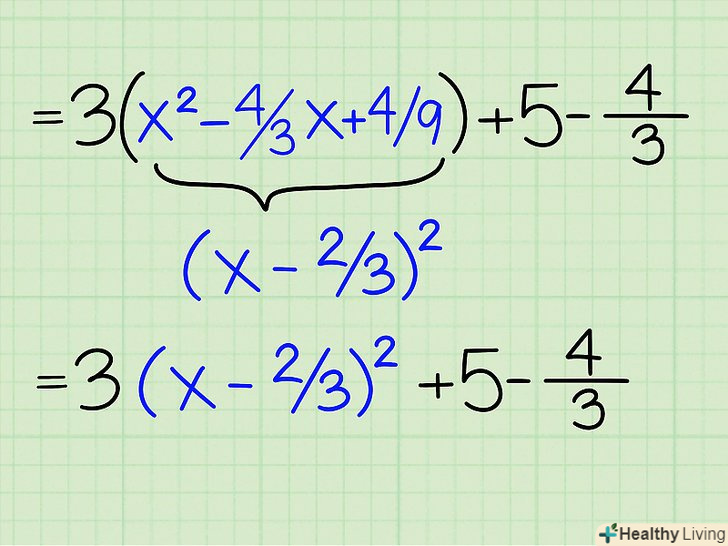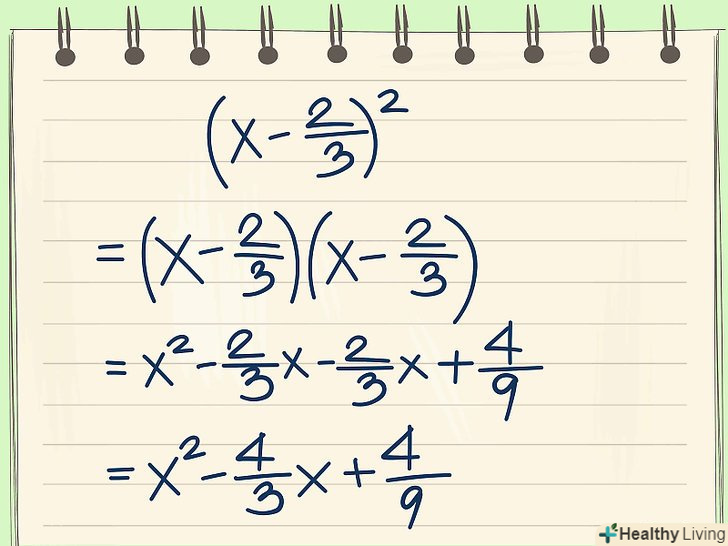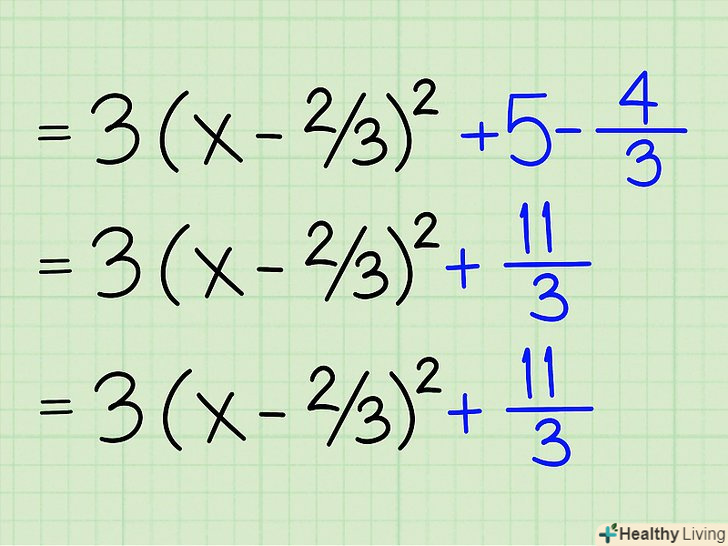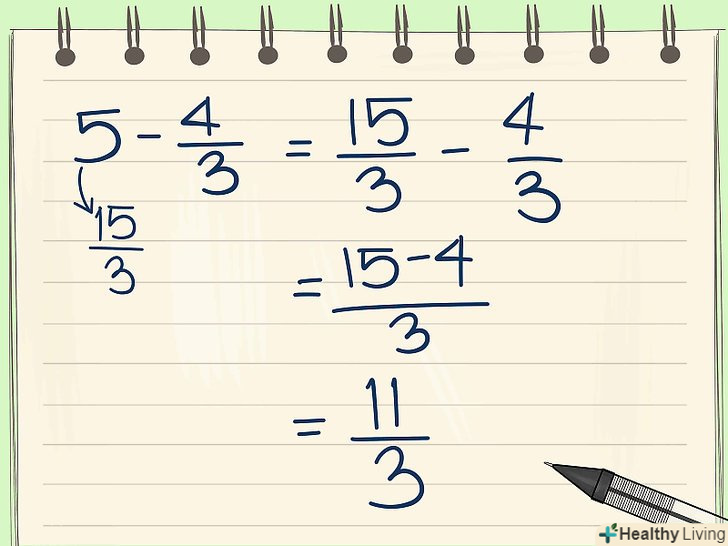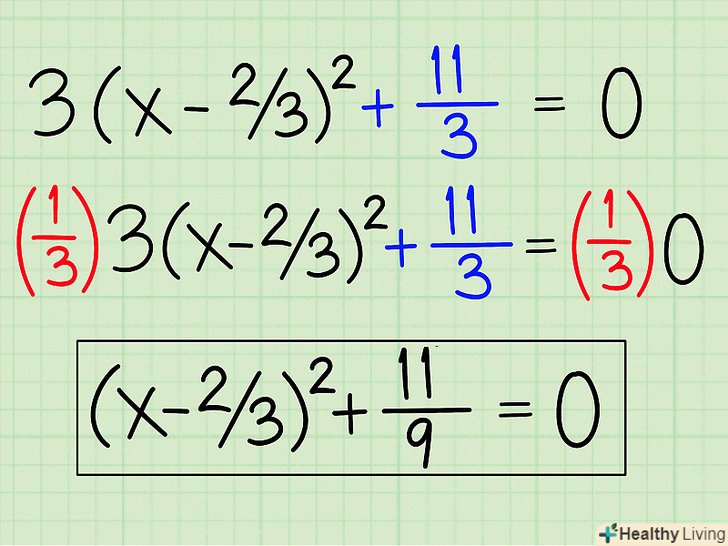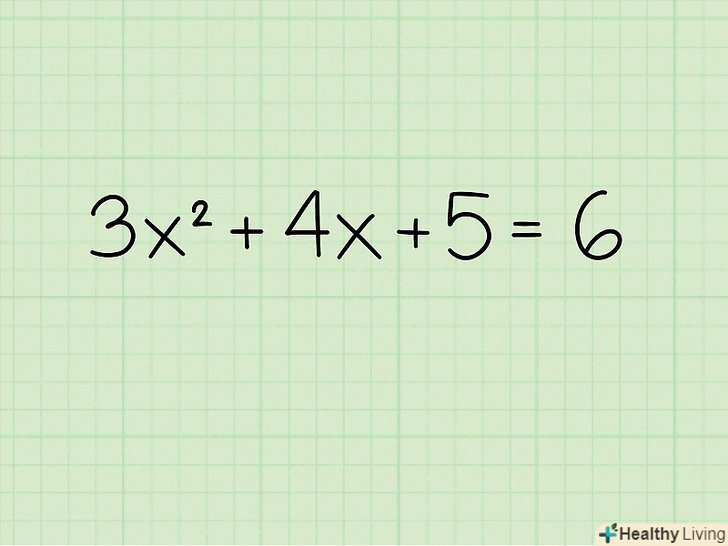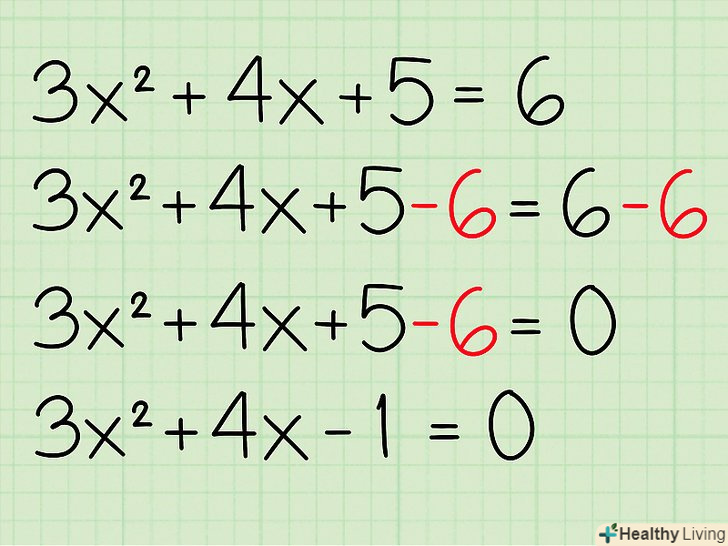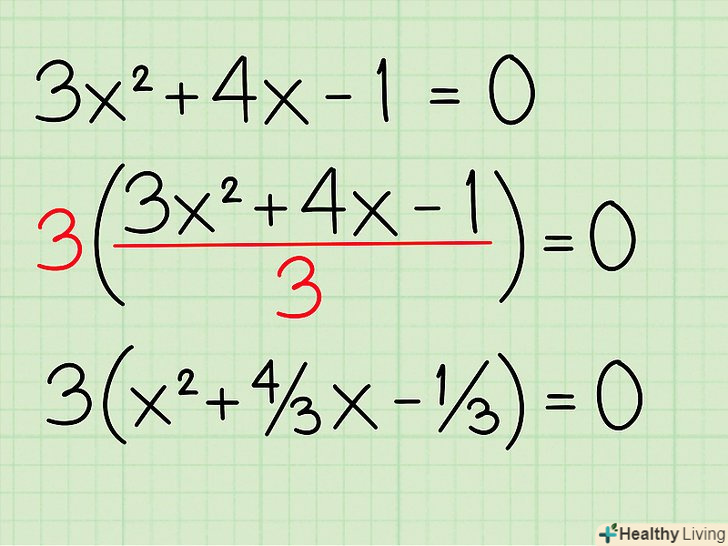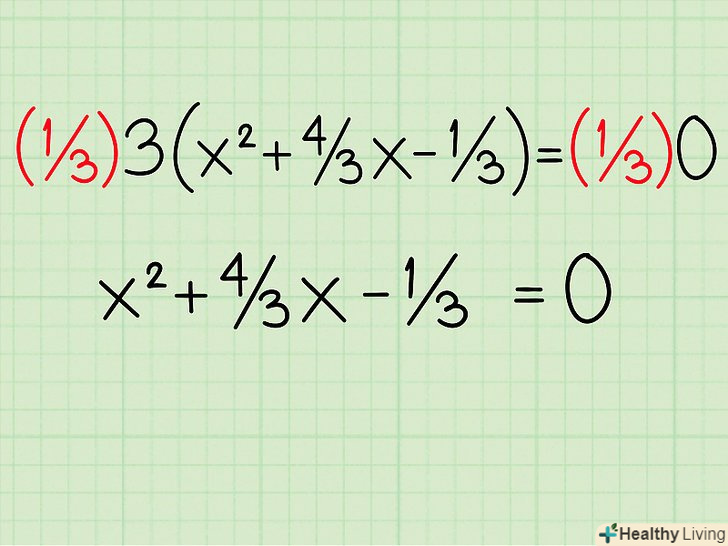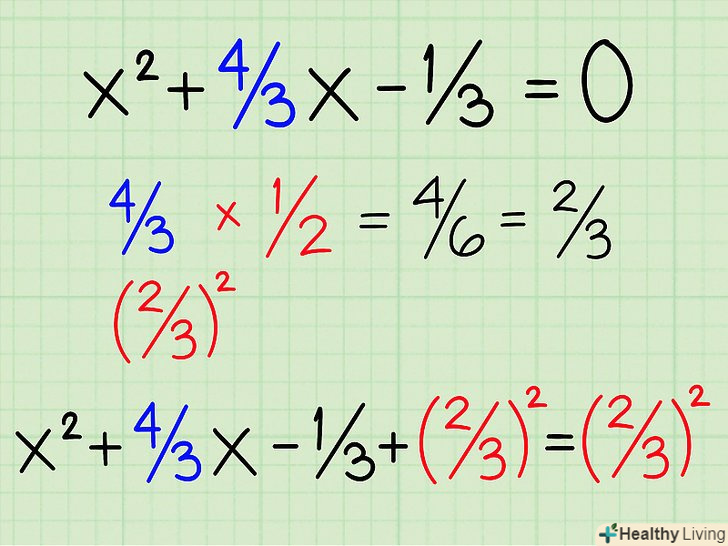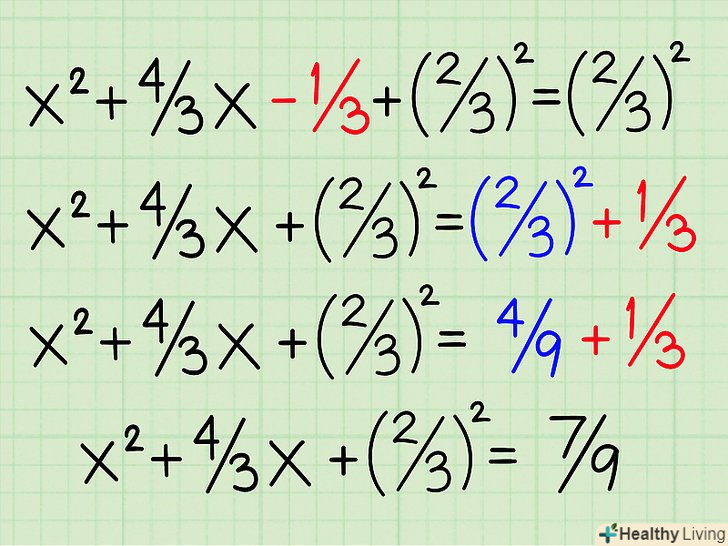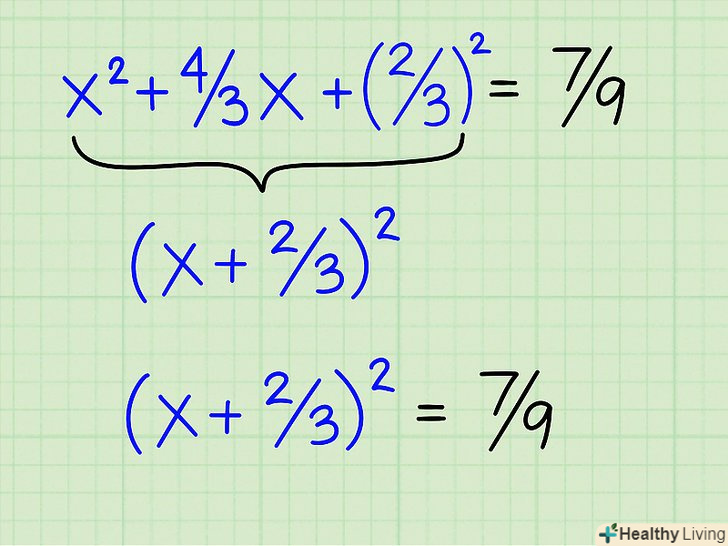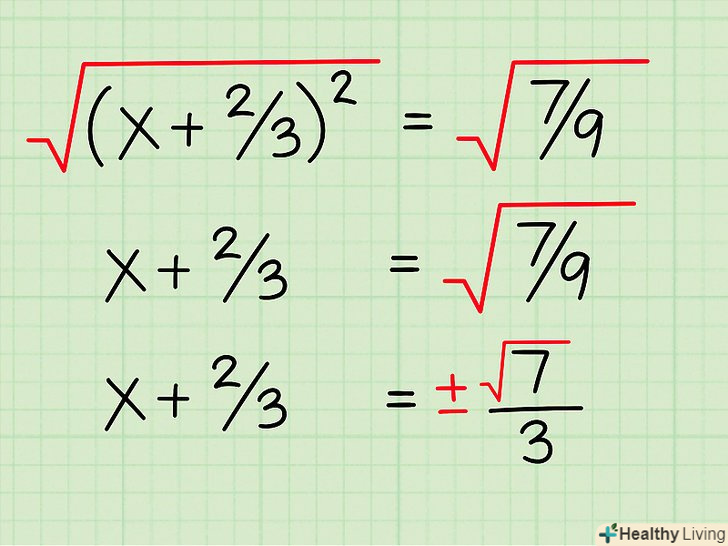Доповнення до повного квадрата-корисний метод, який дозволяє записати квадратне рівняння у формі, легкій для представлення і вирішення. Ви можете доповнити до повного квадрата складне квадратне рівняння і навіть вирішити його. Якщо ви хочете навчитися робити це, виконайте наступні дії.
Кроки
Метод1 З 2:
Перетворення стандартного рівняння до вершинної форми
Метод1 З 2:
 Запишіть рівняння.наприклад, 3x2 - 4x + 5.
Запишіть рівняння.наприклад, 3x2 - 4x + 5. Винесіть за дужки коефіцієнт при перших двох членах. щоб винести за дужки 3 з перших двох членів, розділіть кожен з них на 3. 3x2 ділити на 3 = x2 і 4x ділити на 3 = 4/3x. отже, нове рівняння записується як: 3(x2 - 4 / 3x) + 5. Вільний член 5 залишається за дужками, так як його ми не ділимо на 3.
Винесіть за дужки коефіцієнт при перших двох членах. щоб винести за дужки 3 з перших двох членів, розділіть кожен з них на 3. 3x2 ділити на 3 = x2 і 4x ділити на 3 = 4/3x. отже, нове рівняння записується як: 3(x2 - 4 / 3x) + 5. Вільний член 5 залишається за дужками, так як його ми не ділимо на 3. Ділимо на 2 другий член і зводимо його в квадрат. другим членом, званим b, є 4/3 . Ділимо його на 2: 4/3 ÷ 2 , або 4/3 х 1/2, дорівнює 2/3 . Тепер зводимо це значення в квадрат шляхом зведення в квадрат чисельника і знаменника дробу. (2/3)2 = 4/9.
Ділимо на 2 другий член і зводимо його в квадрат. другим членом, званим b, є 4/3 . Ділимо його на 2: 4/3 ÷ 2 , або 4/3 х 1/2, дорівнює 2/3 . Тепер зводимо це значення в квадрат шляхом зведення в квадрат чисельника і знаменника дробу. (2/3)2 = 4/9. Додайте і відніміть отриману величину до / з рівняння. нам потрібен цей" зайвий " член, щоб доповнити рівняння до повного квадрата. Запам'ятайте, що ви одночасно додаєте і віднімаєте Новий член, тому вихідне рівняння не змінюється. Нове рівняння має виглядати наступним чином: 3 (x2 - 4/3 x + 4/9 - 4/9) + 5.
Додайте і відніміть отриману величину до / з рівняння. нам потрібен цей" зайвий " член, щоб доповнити рівняння до повного квадрата. Запам'ятайте, що ви одночасно додаєте і віднімаєте Новий член, тому вихідне рівняння не змінюється. Нове рівняння має виглядати наступним чином: 3 (x2 - 4/3 x + 4/9 - 4/9) + 5. Винесіть за дужку Новий член зі знаком мінус.оскільки перед дужкою стоїть множник 3, ви не можете просто винести -4 / 9. Спочатку помножте його на 3: -4/9 х 3 = -12/9, або -4/3. Якщо ви працюєте з рівнянням, де коефіцієнт при x2 відсутній (тобто дорівнює 1), то можете пропустити цей крок.
Винесіть за дужку Новий член зі знаком мінус.оскільки перед дужкою стоїть множник 3, ви не можете просто винести -4 / 9. Спочатку помножте його на 3: -4/9 х 3 = -12/9, або -4/3. Якщо ви працюєте з рівнянням, де коефіцієнт при x2 відсутній (тобто дорівнює 1), то можете пропустити цей крок. Перетворіть доданки в дужках в повний квадрат. у дужках залишився вираз: 3(x2 -4 / 3x +4/9). Ви знайшли 4/9, яке доповнює два перших доданків до повного квадрата: 3 (x - 2/3)2. Ви можете перевірити рішення, звівши вираз в дужках в квадрат:
Перетворіть доданки в дужках в повний квадрат. у дужках залишився вираз: 3(x2 -4 / 3x +4/9). Ви знайшли 4/9, яке доповнює два перших доданків до повного квадрата: 3 (x - 2/3)2. Ви можете перевірити рішення, звівши вираз в дужках в квадрат:- 3(x - 2/3)2 =

- 3(x - 2/3)(x -2/3) =
- 3[(x2 -2/3x -2/3x + 4/9)]
- 3(x2 - 4/3x + 4/9)
- 3(x - 2/3)2 =
 Складіть вільні члени. у нас залишилося два вільних члена: 3(x - 2/3)2 - 4/3 + 5. Складіть їх разом: -4/3 + 5 = 11/3. Це можна зробити, привівши їх до спільного знаменника.
Складіть вільні члени. у нас залишилося два вільних члена: 3(x - 2/3)2 - 4/3 + 5. Складіть їх разом: -4/3 + 5 = 11/3. Це можна зробити, привівши їх до спільного знаменника.- -4/3 + 15/3 = 11/3.

- -4/3 + 15/3 = 11/3.
 Запишіть рівняння у вершинній формі. остаточний вигляд рівняння: 3(x - 2/3)2 + 11/3, що відповідає вершинній форміA( x - h)2 + k , де k – вільний член.
Запишіть рівняння у вершинній формі. остаточний вигляд рівняння: 3(x - 2/3)2 + 11/3, що відповідає вершинній форміA( x - h)2 + k , де k – вільний член.
Метод2 З 2:
Рішення квадратного рівняння
Метод2 З 2:
 Запишіть рівняння. наприклад:3x2 + 4x + 5 = 6
Запишіть рівняння. наприклад:3x2 + 4x + 5 = 6 Перенесіть всі члени рівняння на одну сторону і прирівняйте його до 0. у нашому прикладі складіть вільні члени (члени рівняння без змінної): 5+(-6)=-1. Тепер рівняння записується як: 3x2 + 4x - 1 = 0.
Перенесіть всі члени рівняння на одну сторону і прирівняйте його до 0. у нашому прикладі складіть вільні члени (члени рівняння без змінної): 5+(-6)=-1. Тепер рівняння записується як: 3x2 + 4x - 1 = 0. Винесіть за дужку коефіцієнт при змінній вищого порядку. у нашому випадку 3 є коефіцієнтом x2. Тепер рівняння записується у вигляді: 3 (x2 + 4/3x - 1/3) = 0.
Винесіть за дужку коефіцієнт при змінній вищого порядку. у нашому випадку 3 є коефіцієнтом x2. Тепер рівняння записується у вигляді: 3 (x2 + 4/3x - 1/3) = 0. Позбудьтеся від множника перед дужкою. просто перенесіть його в праву частину рівняння (розділіть 0 на 3 = 0). Тепер наше рівняння: x2 + 4/3x - 1/3 = 0
Позбудьтеся від множника перед дужкою. просто перенесіть його в праву частину рівняння (розділіть 0 на 3 = 0). Тепер наше рівняння: x2 + 4/3x - 1/3 = 0 Ділимо на 2 другий член і зводимо його в квадрат. другим членом, званим b, є 4/3 . Ділимо його на 2: 4/3 ÷ 2 , або 4/3 х 1/2=4/6=2/3. Квадрат 2/3 = 4/9. Так як ви додаєте новий член, потрібно додати його до обох сторін рівняння, щоб воно не змінилося:x2 + 4/3 x + 2/32 - 1/3 = 2/32
Ділимо на 2 другий член і зводимо його в квадрат. другим членом, званим b, є 4/3 . Ділимо його на 2: 4/3 ÷ 2 , або 4/3 х 1/2=4/6=2/3. Квадрат 2/3 = 4/9. Так як ви додаєте новий член, потрібно додати його до обох сторін рівняння, щоб воно не змінилося:x2 + 4/3 x + 2/32 - 1/3 = 2/32 Перемістіть вільний член (з вихідного рівняння) з лівого боку рівняння в праву.складіть два вільних члена на правій стороні рівняння, привівши їх до спільного знаменника: 1/3+4/9=3/9+4/9=7/9. Тепер наше рівняння: x2 + 4/3 x + 2/32 = 4/9 + 1/3 і потім: x2 + 4/3 x + 2/32 = 7/9.
Перемістіть вільний член (з вихідного рівняння) з лівого боку рівняння в праву.складіть два вільних члена на правій стороні рівняння, привівши їх до спільного знаменника: 1/3+4/9=3/9+4/9=7/9. Тепер наше рівняння: x2 + 4/3 x + 2/32 = 4/9 + 1/3 і потім: x2 + 4/3 x + 2/32 = 7/9. Запишіть ліву частину рівняння у вигляді квадрата:(x + 2/3)2 . Тепер рівняння запишеться у вигляді: (x + 2/3)2 = 7/9.
Запишіть ліву частину рівняння у вигляді квадрата:(x + 2/3)2 . Тепер рівняння запишеться у вигляді: (x + 2/3)2 = 7/9. Візьміть квадратний корінь з обох сторін рівняння. квадратний корінь з (x + 2/3)2 = x + 2/3. На правій стороні отримаємо +/-( √ 7)/3. Квадратний корінь з знаменника 9 = 3, а квадратний корінь з 7= √7. Не забудьте написати +/ -, тому що квадратний корінь може бути позитивним або негативним.
Візьміть квадратний корінь з обох сторін рівняння. квадратний корінь з (x + 2/3)2 = x + 2/3. На правій стороні отримаємо +/-( √ 7)/3. Квадратний корінь з знаменника 9 = 3, а квадратний корінь з 7= √7. Не забудьте написати +/ -, тому що квадратний корінь може бути позитивним або негативним. Виділіть змінну. для виділення змінної х перенесіть вільний член 2/3 в праву частину рівняння. Тепер у вас є два можливих значення х: +/-( √ 7)/3 - 2/3. Це ваші дві відповіді. Ви можете залишити все як є або знайти фактичний квадратний корінь з 7, якщо потрібно дати відповідь без кореня.
Виділіть змінну. для виділення змінної х перенесіть вільний член 2/3 в праву частину рівняння. Тепер у вас є два можливих значення х: +/-( √ 7)/3 - 2/3. Це ваші дві відповіді. Ви можете залишити все як є або знайти фактичний квадратний корінь з 7, якщо потрібно дати відповідь без кореня.
Поради
- Не забудьте записати + / - перед коренем; в іншому випадку ви отримаєте тільки одну відповідь.
- Навіть після ви знаєте формулу рішення квадратного рівняння, періодично практикуйтеся в доповненні до повного квадрата. Таким чином, ви не забудете, як це зробити, коли Вам це знадобиться.