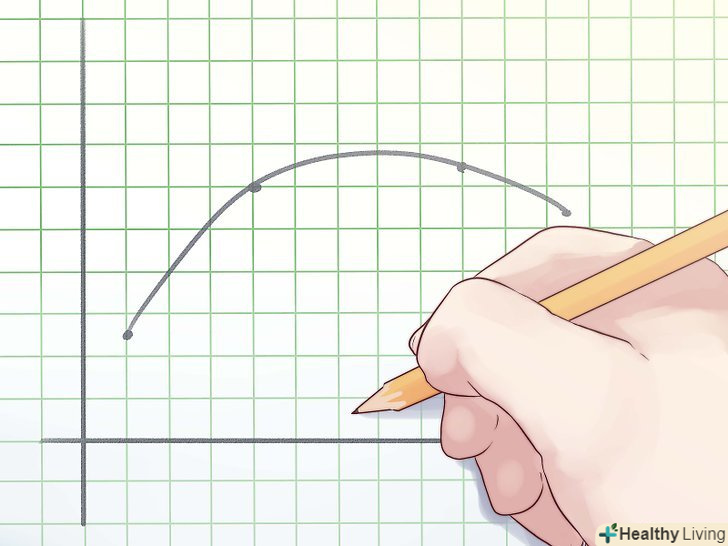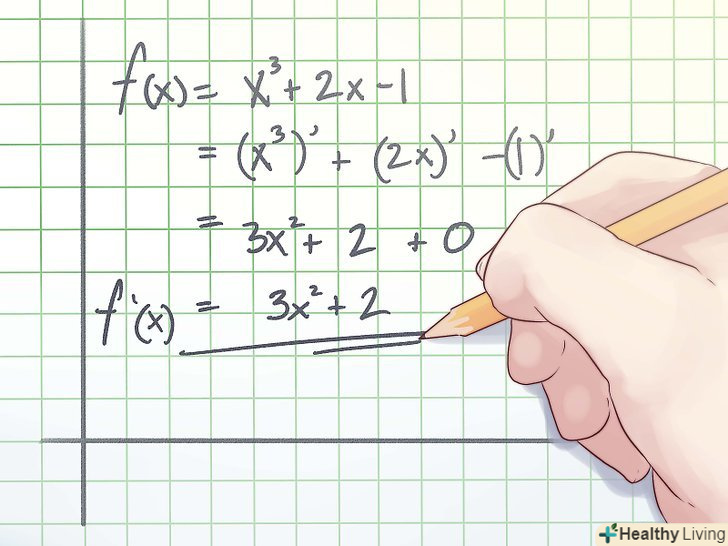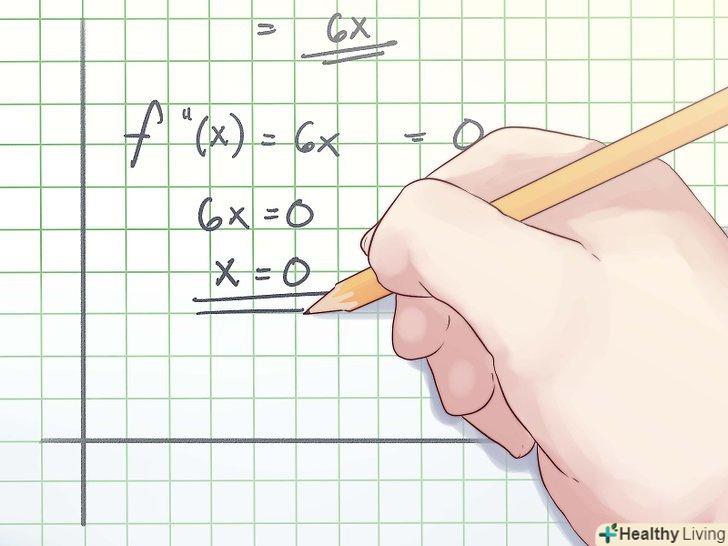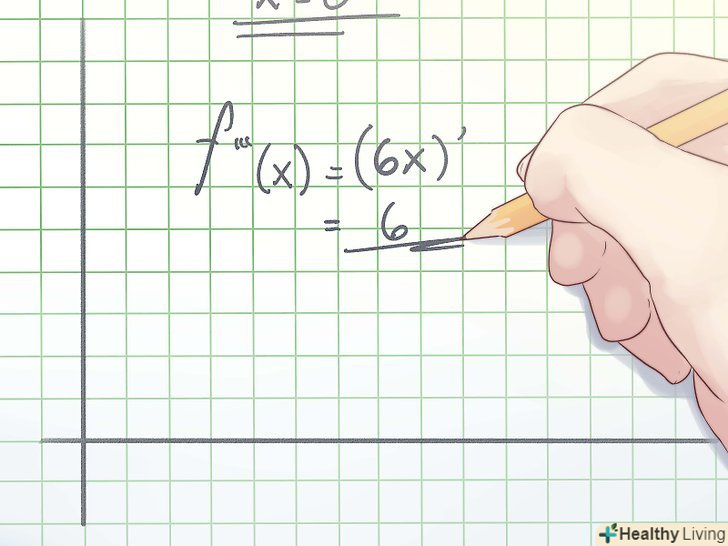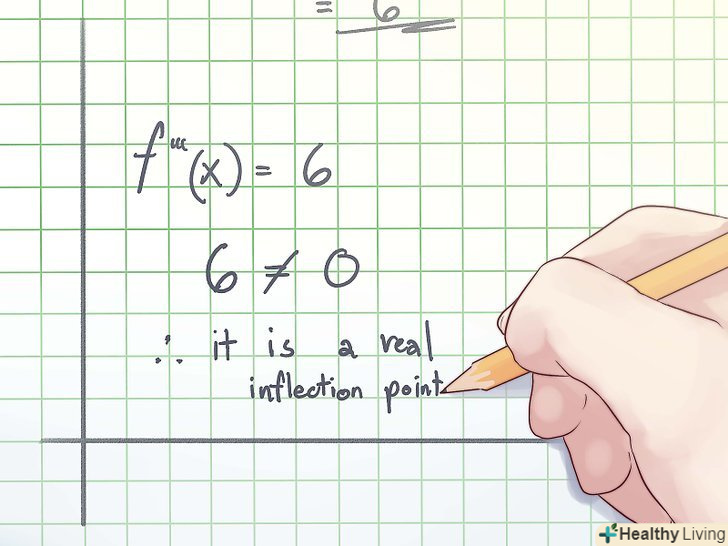В диференціальному обчисленні точка перегину - ця точка кривої, в якій її кривизна змінює знак (з плюса на мінус або з мінуса на плюс). Це поняття використовується в машинобудуванні, економіці та статистиці для визначення істотних змін в даних.
Кроки
Метод1З 3:
Частина 1: визначення точки перегину
Метод1З 3:
Визначення увігнутої функції. Середина будь хорди (відрізок, що з'єднує дві точки) графіка увігнутої функції лежить або під графіком, або на ньому.-
Визначення опуклої функції. Середина будь хорди (відрізок, що з'єднує дві точки) графіка опуклою функції лежить або над графіком, або на ньому.
-
Визначення коренів функції. корінь функції-це таке значення змінної "х", при якому у = 0.
- При побудові графіка функції коріння-це точки, в яких графік перетинає вісь х.
Метод2 З 3:
Обчислення похідних функції
Метод2 З 3:
-
Знайдіть першу похідну функції.подивіться правила диференціювання в підручнику; ви повинні навчитися брати перші похідні, і тільки потім переходити до більш складних обчислень. Перші похідні позначаються як f '(х). Для виразів виду ax^p + bx^(p−1) + cx + d перша похідна має вигляд: apx^(p−1) + b(p − 1)x^(p−2) + C.
- Наприклад, знайдіть точки перегину функції f (х) = х^3 +2х -1. Перша похідна цієї функції має вигляд:
f '(x) = (x^3 + 2x − 1)' = (x^3)' + (2x)' − (1)' = 3x^2 + 2 + 0 = 3x2 + 2
- Наприклад, знайдіть точки перегину функції f (х) = х^3 +2х -1. Перша похідна цієї функції має вигляд:
-
Знайдіть другу похідну функції.друга похідна-це похідна від першої похідної вихідної функції. Друга похідна позначається як f "(x).
- У наведеному вище прикладі друга похідна має вигляд:
f "(x) = (3x2 + 2) ' = 2 x 3 x x + 0 = 6x
- У наведеному вище прикладі друга похідна має вигляд:
-
Прирівняйте другу похідну до нуля і вирішіть отримане рівняння.отриманий результат буде передбачуваною точкою перегину.
- У наведеному вище прикладі ваш розрахунок виглядає наступним чином:
f "(x) = 0
6x = 0
x=0
- У наведеному вище прикладі ваш розрахунок виглядає наступним чином:
-
Знайдіть третю похідну функції. щоб переконатися, що отриманий результат насправді є точкою перегину, знайдіть третю похідну, яка є похідною від другої похідної вихідної функції. Третя похідна позначається як f " '(x).
- У наведеному вище прикладі третя похідна має вигляд:
f "'(x) = (6x)' = 6
- У наведеному вище прикладі третя похідна має вигляд:
Метод3 З 3:
Частина 3: Пошук точки перегину
Метод3 З 3:
-
Перевірте третю похідну.стандартне правило оцінки передбачуваної точки перегину: якщо третя похідна не дорівнює нулю(тобто f "'(x) ≈ 0), то передбачувана точка перегину є справжньою точкою перегину. Перевірте третю похідну; якщо вона не дорівнює нулю, то Ви знайшли СПРАВЖНЮ точку перегину.
- У наведеному вище прикладі третя похідна дорівнює 6, а не 0. Тому Ви знайшли СПРАВЖНЮ точку перегину.
-
Знайдіть координати точки перегину.координати точки перегину позначаються як (x, f (x)), де х - значення незалежної змінної «х» в точці перегину, f(х) - значення залежної змінної «у» в точці перегину.
- У наведеному вище прикладі при прирівнюванні другої похідної до нуля Ви знайшли, що х = 0. Таким чином, щоб визначити координати точки перегину, знайдіть f(0). Ваш розрахунок виглядає наступним чином:
f(0) = 0^3 +2×0-1 = -1.
- У наведеному вище прикладі при прирівнюванні другої похідної до нуля Ви знайшли, що х = 0. Таким чином, щоб визначити координати точки перегину, знайдіть f(0). Ваш розрахунок виглядає наступним чином:
-
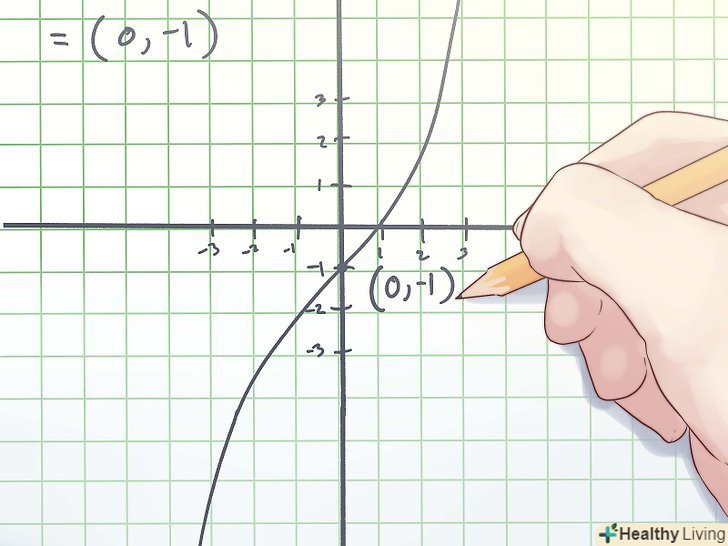
Запишіть координати точки перегину.координати точки перегину-це знайдені значення " х " і f(x).
- У наведеному вище прикладі точка перегину-це точка з координатами (0, -1).
Поради
- Перша похідна від вільного члена (простого числа) завжди дорівнює нулю.
