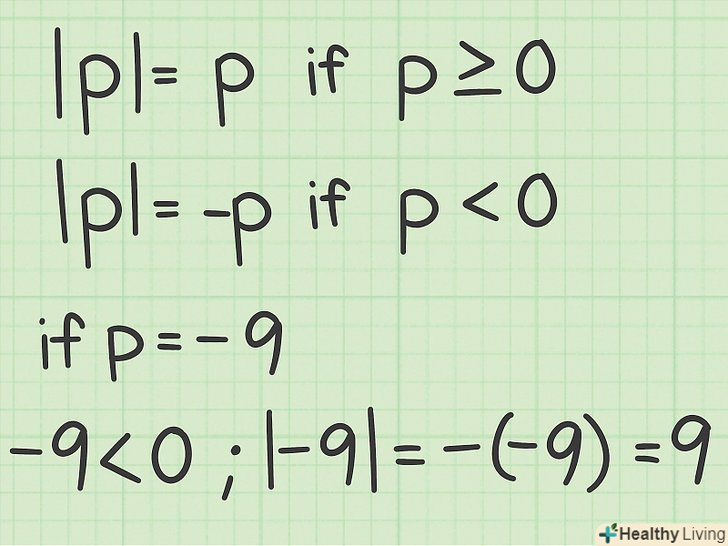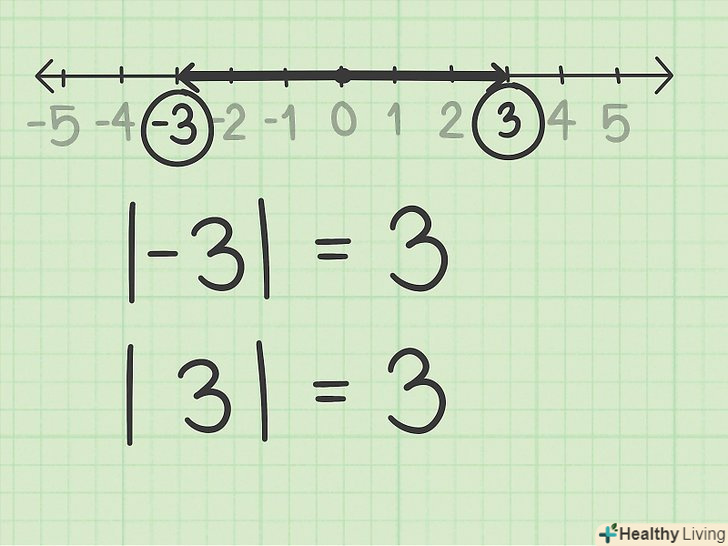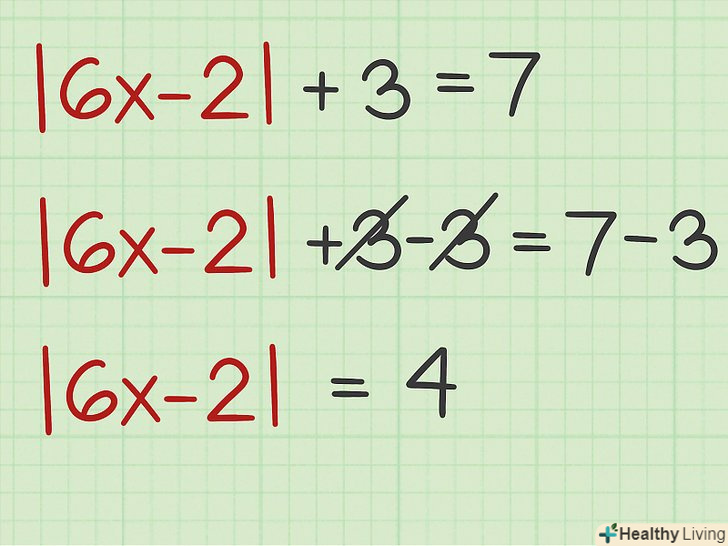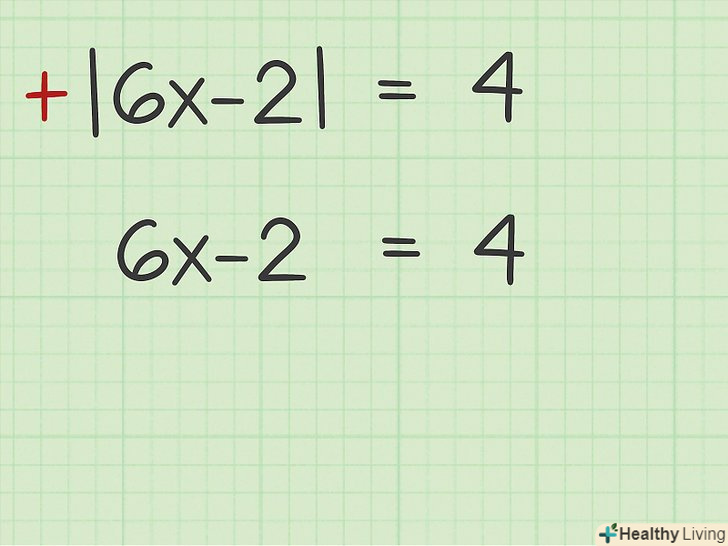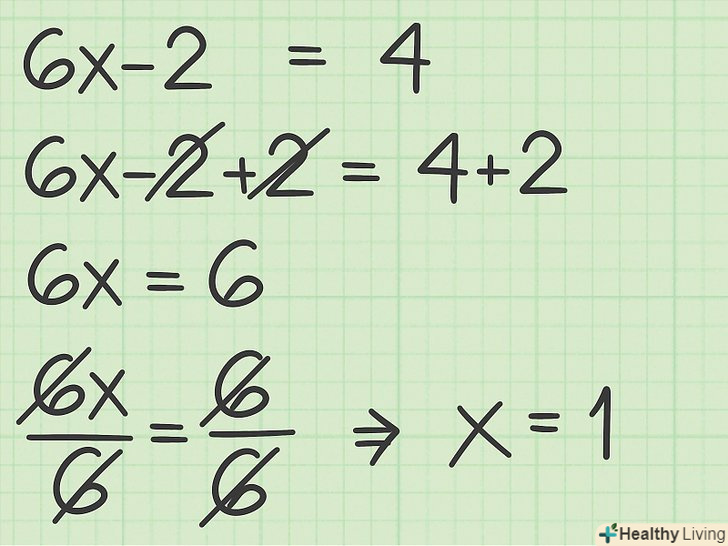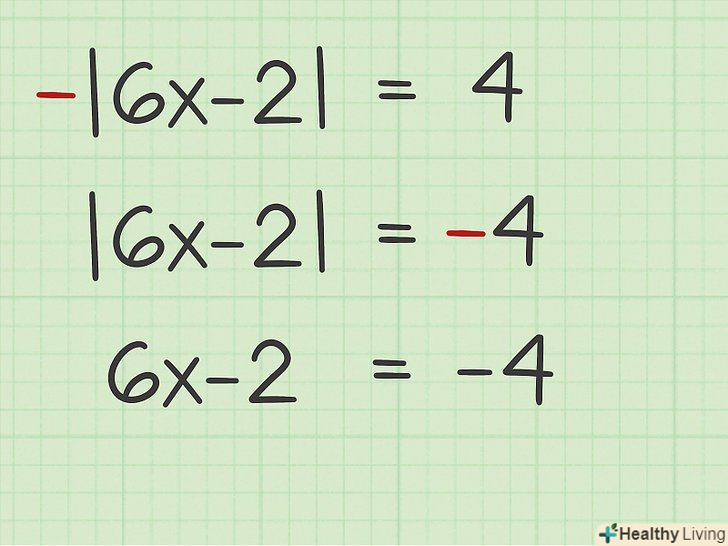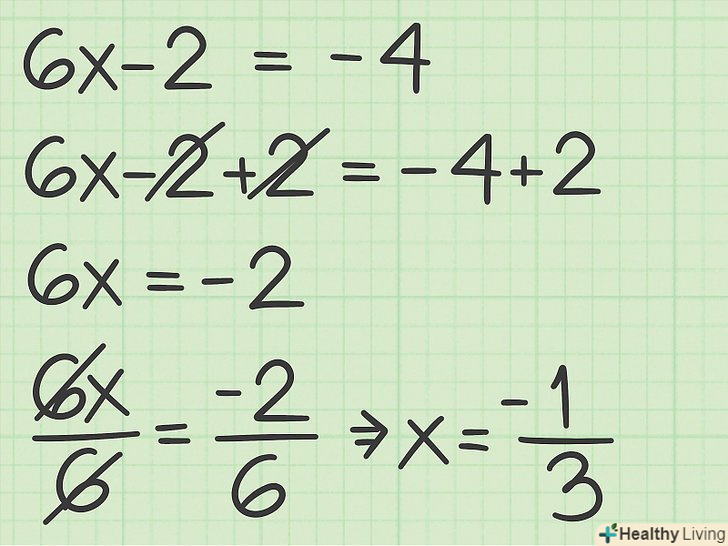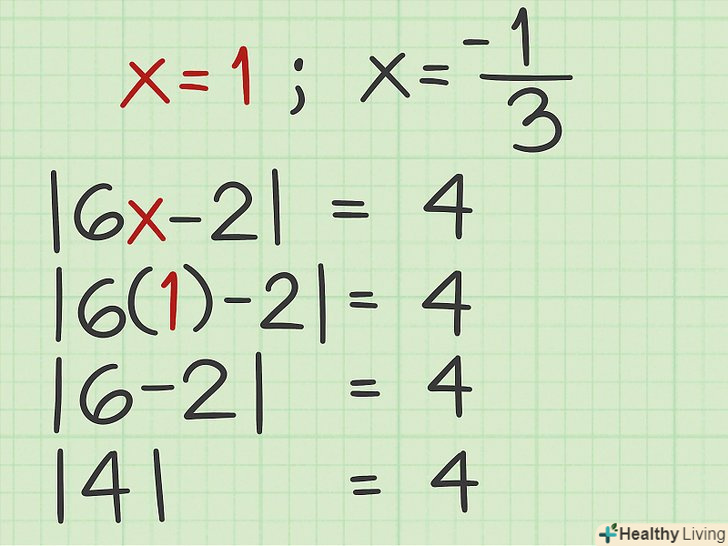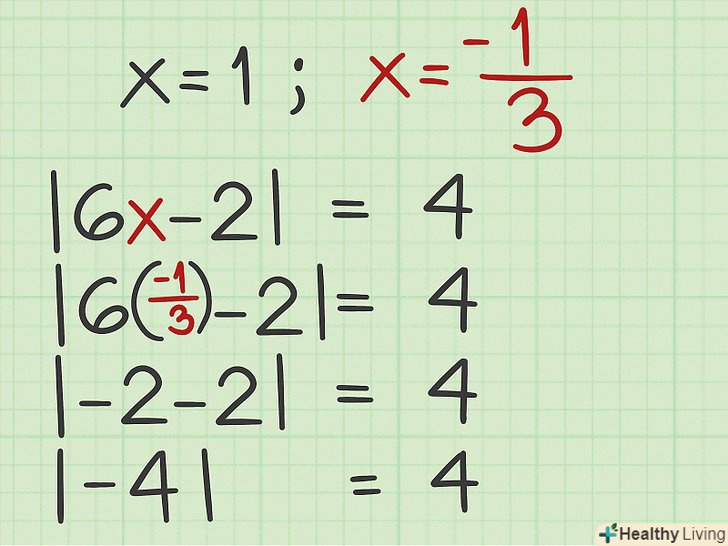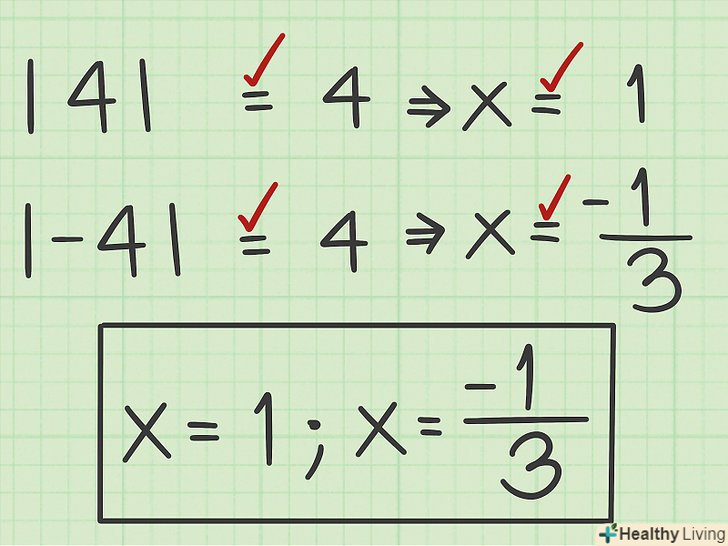Рівнянням з модулем (абсолютною величиною) є будь-яке рівняння, в якому змінна або вираз укладено в модульні дужки. Абсолютна величина змінної позначається як
, а значення модуля завжди позитивно (за винятком нуля, який не є ні позитивним, ні негативним числом). Рівняння з абсолютною величиною вирішується як будь-яке інше математичне рівняння, але рівняння з модулем може мати два кінцевих результату, тому що потрібно вирішити позитивне і негативне рівняння.
Кроки
Частина1З 3:
Запис рівняння
Частина1З 3:
 Зрозумійте математичне визначення модуля. він визначається так:
Зрозумійте математичне визначення модуля. він визначається так:. Це означає, що якщо число
позитивно, модуль дорівнює
. Якщо число
негативно, модуль дорівнює
. Так як мінус на мінус дає плюс, модуль
позитивний.[1]
- Наприклад, |9| = 9; |-9| = -(- 9) = 9.
 Усвідомте поняття абсолютної величини з геометричної точки зору.Модуль числа дорівнює відстані між початком координат і цим числом.[2] Модуль позначається модульними лапками, в які полягає число, змінна або вираз (
Усвідомте поняття абсолютної величини з геометричної точки зору.Модуль числа дорівнює відстані між початком координат і цим числом.[2] Модуль позначається модульними лапками, в які полягає число, змінна або вираз (). Модуль числа завжди позитивний.[3]
- Наприклад,
і
. Обидва числа -3 і 3 знаходяться на відстані трьох одиниць від 0.
- Наприклад,
 У рівнянні ізолюйте модуль. абсолютна величина повинна знаходитися на одній стороні рівняння. Будь-які числа або члени поза модульних дужок потрібно перенести на іншу сторону рівняння.[4] зверніть увагу, що модуль не може дорівнювати негативному числу, тому, якщо після ізолювання модуля він дорівнює негативному числу, таке рівняння не має рішення.[5]
У рівнянні ізолюйте модуль. абсолютна величина повинна знаходитися на одній стороні рівняння. Будь-які числа або члени поза модульних дужок потрібно перенести на іншу сторону рівняння.[4] зверніть увагу, що модуль не може дорівнювати негативному числу, тому, якщо після ізолювання модуля він дорівнює негативному числу, таке рівняння не має рішення.[5]- Наприклад, дано рівняння
; щоб ізолювати модуль, з обох сторін рівняння відніміть 3:
- Наприклад, дано рівняння
Частина2З 3:
Рішення рівняння
Частина2З 3:
 Запишіть рівняння для позитивного значення.рівняння з модулем мають два рішення. Щоб записати позитивне рівняння, позбудьтеся від модульних дужок, а потім вирішіть отримане рівняння (як завжди).[6]
Запишіть рівняння для позитивного значення.рівняння з модулем мають два рішення. Щоб записати позитивне рівняння, позбудьтеся від модульних дужок, а потім вирішіть отримане рівняння (як завжди).[6]- Наприклад, позитивним рівнянням дляSpan class= "mwe-math-mathml-inline mwe-math-mathml-a11y "style=" display: none; "data-original-text=||6x-2/=4"
є
.
- Наприклад, позитивним рівнянням дляSpan class= "mwe-math-mathml-inline mwe-math-mathml-a11y "style=" display: none; "data-original-text=||6x-2/=4"
 Вирішіть позитивне рівняння.для цього обчисліть значення змінної за допомогою математичних операцій. Так можна знайти перше можливе рішення рівняння.
Вирішіть позитивне рівняння.для цього обчисліть значення змінної за допомогою математичних операцій. Так можна знайти перше можливе рішення рівняння.- Наприклад:
- Наприклад:
 Запишіть рівняння для від'ємного значення. щоб записати негативне рівняння, позбудьтеся від модульних дужок, а на іншій стороні рівняння перед числом або виразом поставте знак «мінус».[7]
Запишіть рівняння для від'ємного значення. щоб записати негативне рівняння, позбудьтеся від модульних дужок, а на іншій стороні рівняння перед числом або виразом поставте знак «мінус».[7]- Наприклад, негативним рівнянням для
є
.
- Наприклад, негативним рівнянням для
 Вирішіть негативне рівняння.для цього обчисліть значення змінної за допомогою математичних операцій. Так можна знайти друге можливе рішення рівняння.
Вирішіть негативне рівняння.для цього обчисліть значення змінної за допомогою математичних операцій. Так можна знайти друге можливе рішення рівняння.- Наприклад:
- Наприклад:
Частина3З 3:
Перевірка рішення
Частина3З 3:
 Перевірте результат рішення позитивного рівняння. для цього отримане значення підставте у вихідне рівняння[8], тобто підставте значення
Перевірте результат рішення позитивного рівняння. для цього отримане значення підставте у вихідне рівняння[8], тобто підставте значення, знайдене в результаті рішення позитивного рівняння, у вихідне рівняння з модулем. Якщо дотримується рівність, рішення вірно.
- Наприклад, якщо в результаті рішення позитивного рівняння Ви знайшли, що
, підставте
в вихідне рівняння:
- Наприклад, якщо в результаті рішення позитивного рівняння Ви знайшли, що
 Перевірте результат рішення від'ємного рівняння.якщо одне з рішень правильне, це ще не означає, що і друге рішення буде вірним. Тому підставте значення
Перевірте результат рішення від'ємного рівняння.якщо одне з рішень правильне, це ще не означає, що і друге рішення буде вірним. Тому підставте значення, знайдене в результаті рішення негативного рівняння, у вихідне рівняння з модулем.
- Наприклад, якщо в результаті рішення негативного рівняння Ви знайшли, що
, підставте
в вихідне рівняння:
- Наприклад, якщо в результаті рішення негативного рівняння Ви знайшли, що
 Зверніть увагу на дійсні рішення.рішення рівняння є дійсним (вірним), якщо при підстановці у вихідне рівняння дотримується рівність.Майте на увазі, що рівняння може мати два, одне або жодного дійсного рішення.
Зверніть увагу на дійсні рішення.рішення рівняння є дійсним (вірним), якщо при підстановці у вихідне рівняння дотримується рівність.Майте на увазі, що рівняння може мати два, одне або жодного дійсного рішення.- У нашому прикладі
і
, тобто дотримуються рівності і обидва рішення є дійсними. Таким чином, рівняння
має два можливих рішення:
,
.
- У нашому прикладі
Поради
- Пам'ятайте, що модульні дужки відрізняються від інших типів дужок за виглядом і функціональністю.
Джерела
- ↑ Http://tutorial.math.lamar.edu/Classes/Alg/SolveAbsValueEqns.aspx
- ↑ Https://www.mathsisfun.com/numbers/absolute-value.html
- ↑ Http://www.varsitytutors.com/high_school_math-help/solving-absolute-value-equations
- ↑ Http://www.purplemath.com/modules/solveabs.htm
- ↑ Http://www.varsitytutors.com/high_school_math-help/solving-absolute-value-equations
- ↑ Http://www.purplemath.com/modules/solveabs.htm
- ↑ Https://www.khanacademy.org/math/algebra/absolute-value-equations-functions/absolute-value-equations/v/absolute-value-equations
- ↑ Http://www.varsitytutors.com/high_school_math-help/solving-absolute-value-equations