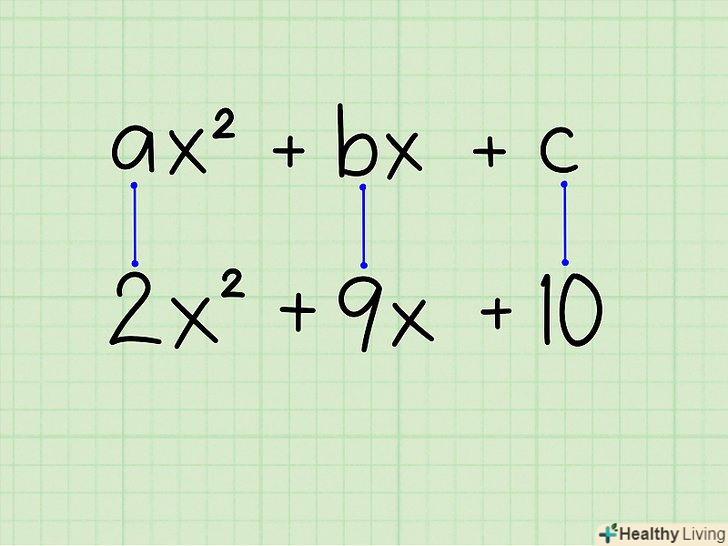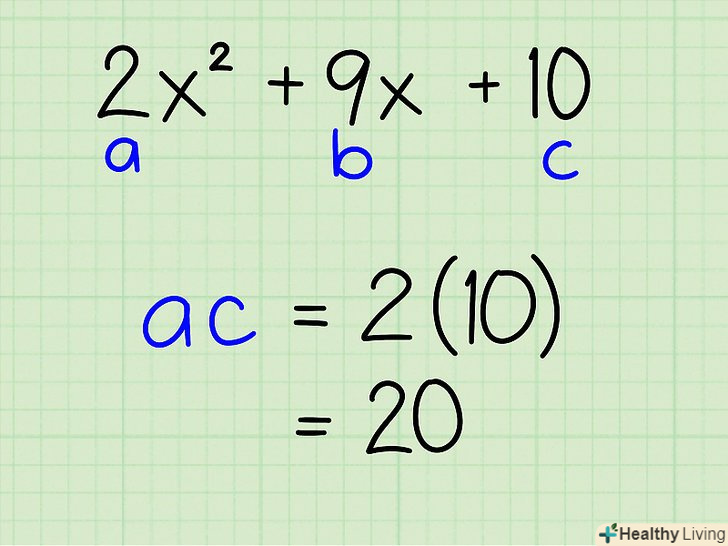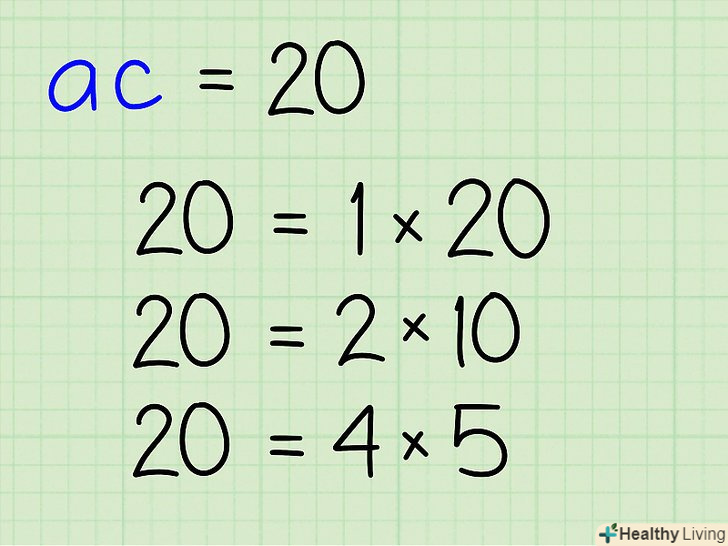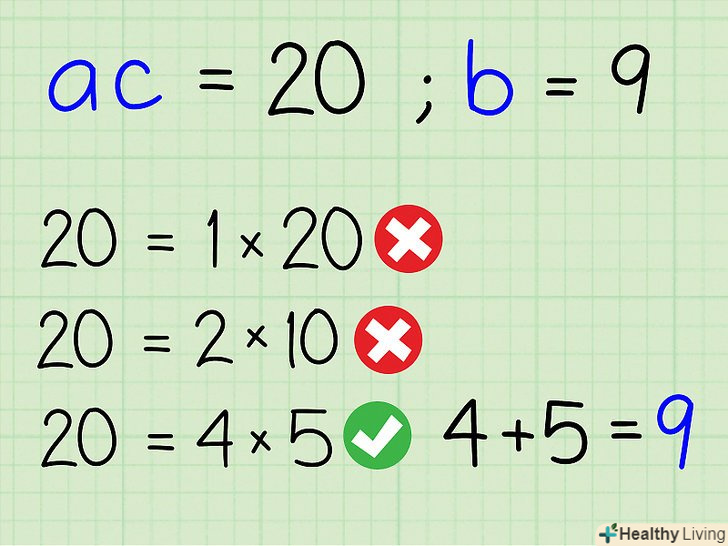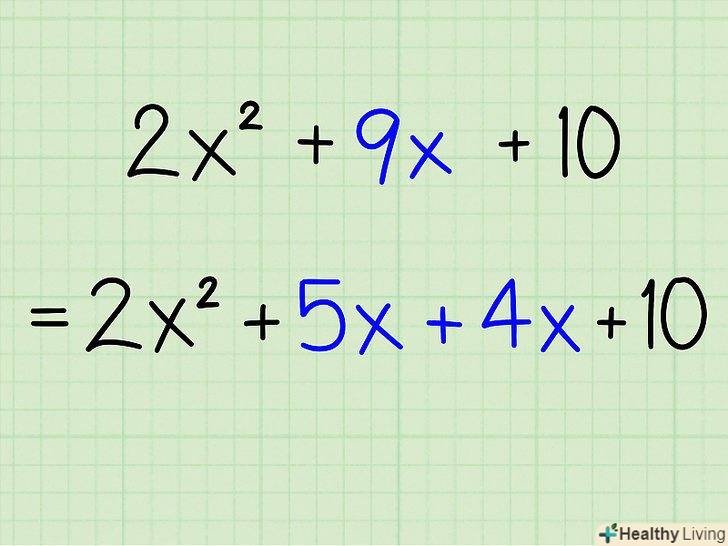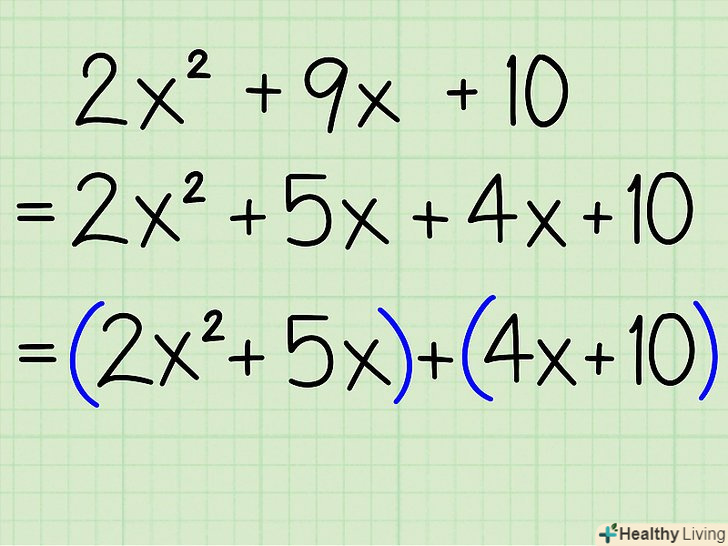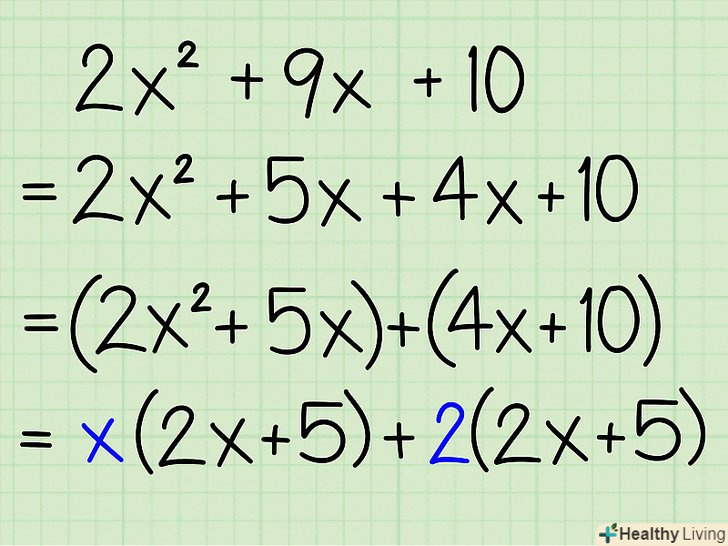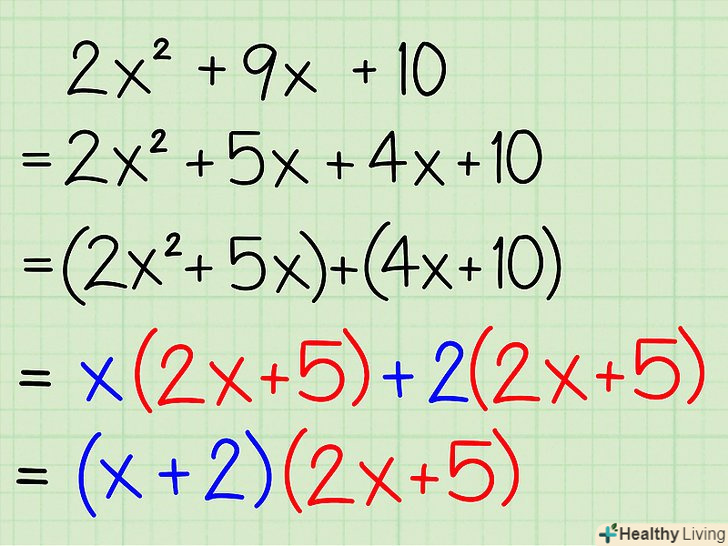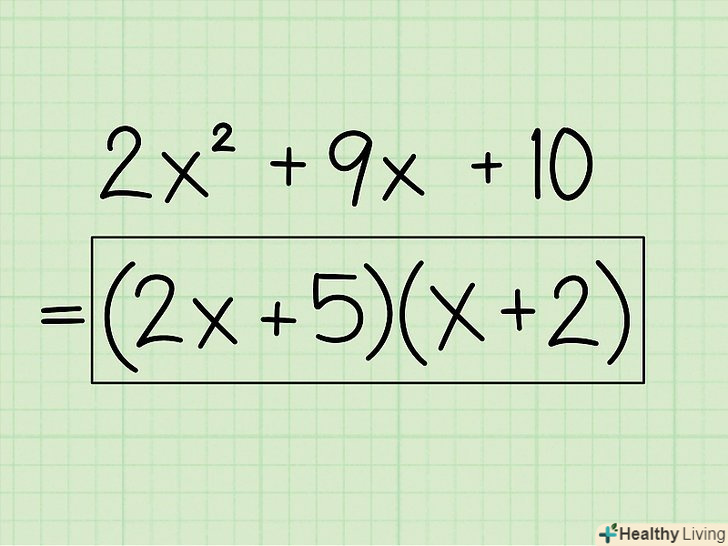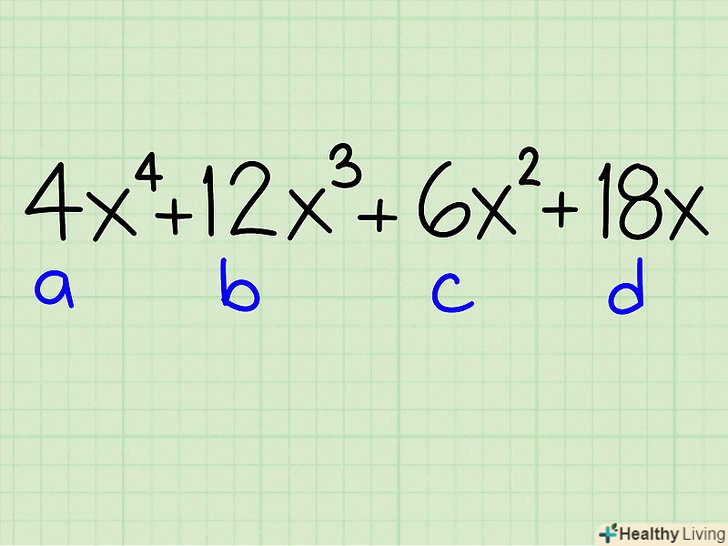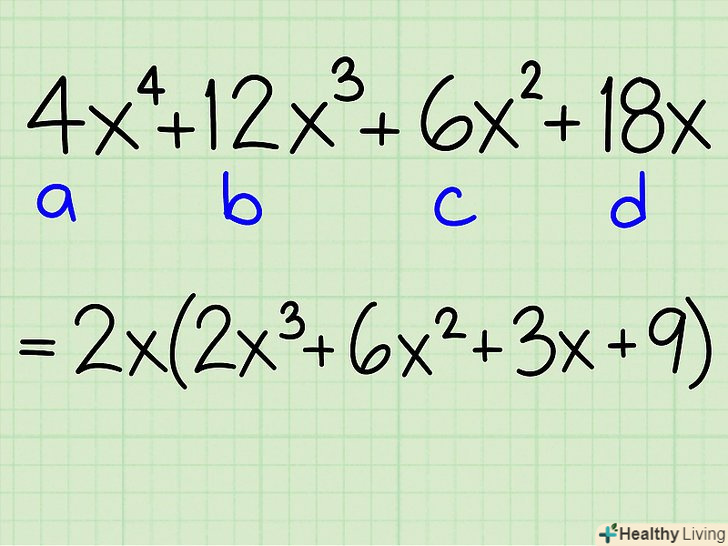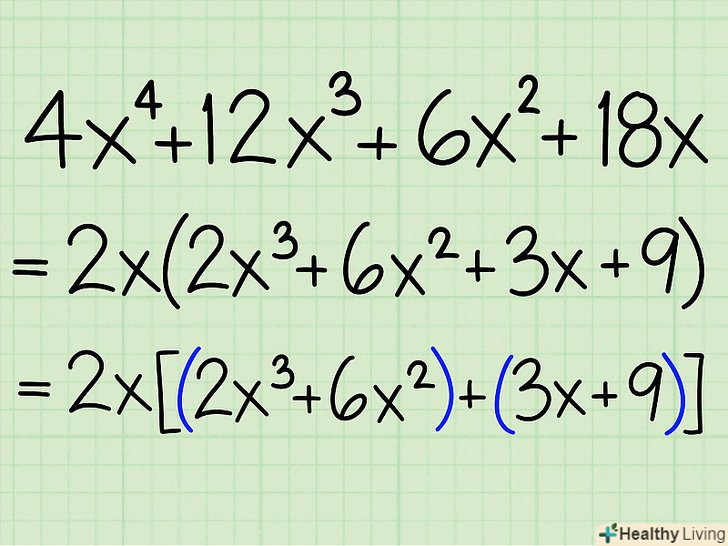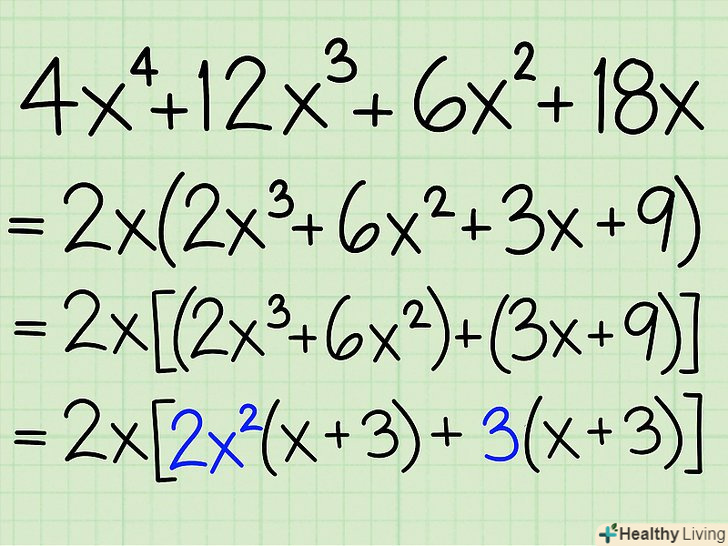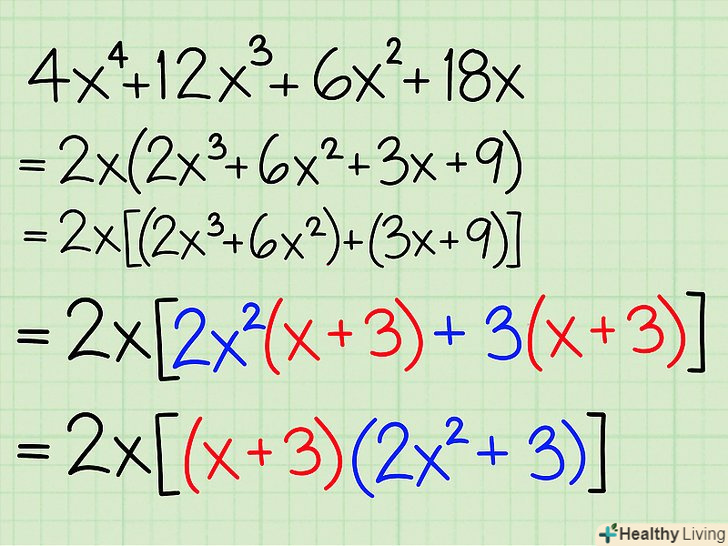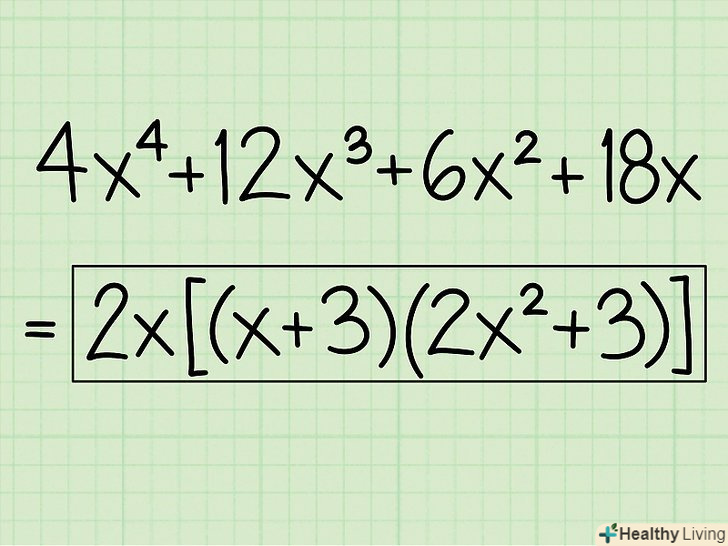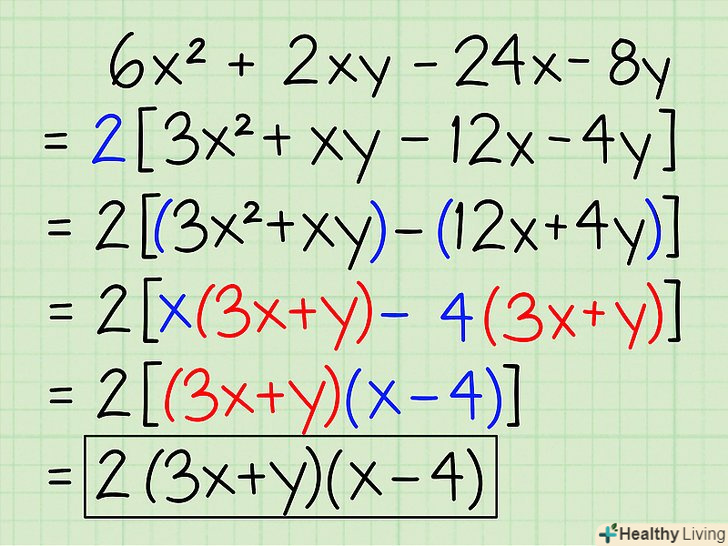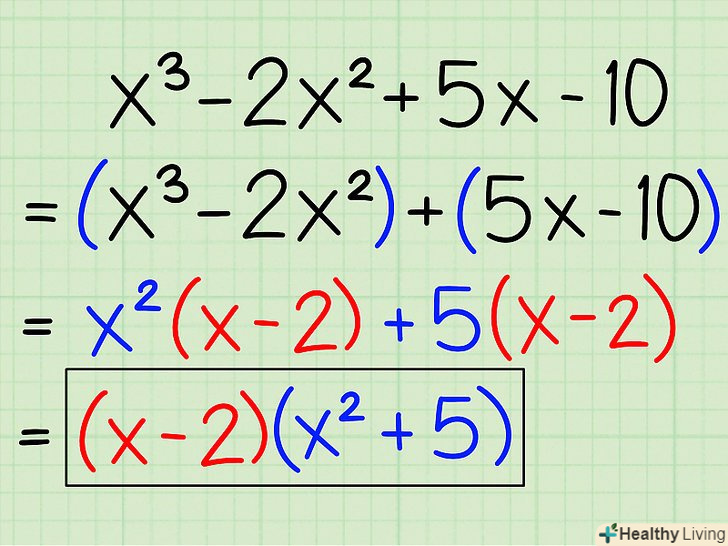1. Головна
    2. Математика
    3. Як розкладати на множники способом угруповання

Як розкладати на множники способом угруповання

Ця стаття розповість вам, як розкладати рівняння на множники способом угруповання. Описані способи застосовні для розкладання квадратних рівнянь і рівнянь з чотирма членами.

Метод1 З 2:
Квадратне рівняння[1][2]

  1. Квадратне рівняння має вигляд: ax2 + bx + c
    • Цей метод, як правило, застосовується у випадках, коли а &#gt; 1, але може застосовуватися і при А = 1.
    • Приклад: 2x2 + 9x + 10
  2. Перемножте коефіцієнти А і С.
    • Приклад: 2x2 + 9x + 10
      • A = 2; c = 10
      • A * c = 2 * 10 = 20
  3. Для отриманого значення знайдіть всі можливі пари множників.
    • Приклад: множники числа 20: 1, 2, 4, 5, 10, 20.
      • Пари множників: (1, 20), (2, 10), (4, 5).
  4. Знайдіть пару множників, сума яких дорівнює коефіцієнту b.
    • Якщо результат добутку а на С негативний, то знайдіть пару множників, різниця яких дорівнює коефіцієнту b.
    • Приклад: 2x2 + 9x + 10
      • B = 9
      • 1 + 20 = 21 – не підходить.
      • 2 + 10 = 12 – не підходить.
      • 4 + 5 = 9 – підходить.
  5. Розбийте член рівняння з коефіцієнтом b відповідно до знайдених парами множників.не забудьте записати правильні знаки (плюс або мінус).
    • Зверніть увагу, що порядок отриманих двох членів значення не має – це не позначиться на кінцевому результаті.
    • Приклад: 2x2 + 9x + 10 = 2x 2 + 5x + 4x + 10
  6. Згрупуйте члени рівняння: розгляньте перші два члени (як пару) і другі два члени (теж як пару).
    • Приклад: 2x2 + 5x + 4x + 10 = (2x 2 + 5x) +(4x + 10)
  7. У кожній парі членів рівняння винесіть за дужку загальний множник.
    • Приклад: х(2x + 5) + 2(2x + 5)
  8. У двох дужках виходить один і той же вираз.запишіть його як є, а у другі дужки запишіть множники, що стоять за дужками.
    • Приклад: (2x + 5) (х + 2)
  9. Запишіть відповідь.
    • Приклад: 2x2 + 9x + 10 = (2x + 5)(x + 2)
      • Остаточна відповідь: (2x + 5) (х + 2)

Додаткові приклади

  1. Розкладіть на множники 4x2 - 3x - 10
    • A * c = 4 * -10 = -40
    • Пари множників числа 40: (1, 40), (2, 20), (4, 10), (5, 8).
    • Відповідна пара: (5, 8); 5 - 8 = -3
    • 4x2 - 8x + 5x - 10
    • (4x2 - 8x) + (5x - 10)
    • 4x(x - 2) + 5(x - 2)
    • (x - 2)(4x + 5)
  2. Розкладіть на множники: 8x2 + 2x-3
    • A * c = 8 * -3 = -24
    • Пари множників числа 24: (1, 24), (2, 12), (4, 6)
    • Відповідна пара: (4, 6); 6 - 4 = 2
    • 8x2 + 6x - 4x - 3
    • (8x2 + 6x) - (4x + 3)
    • 2x(4x + 3) - 1(4x + 3)
    • (4x + 3)(2x - 1)

Метод2 З 2:
Рівняння з чотирма членами[3][4]

  1. Для застосування цього методу рівняння повинно включати чотири члени.
    • Наприклад, рівняння може мати такий вигляд: ax3 + bx2 + cx + d
    • Або такий вид:
      • Axy + by + cx + d
      • Ax2 + bx + cxy + dy
      • Ax4 + bx3 + cx2 + dx
      • Або аналогічний.
    • Приклад: 4x4 + 12x 3 + 6x2 + 18x
  2. Винесіть за дужки найбільший спільний дільник (НСД). НСД - це найбільше число (вираз), на яке діляться всі члени даного рівняння.
    • Якщо НСД = 1, за дужки нічого не виносьте.
    • При винесенні множника за дужки пишіть його в процесі ваших обчислень – він включається в остаточну відповідь.
    • Приклад: 4x4 + 12x 3 + 6x2 + 18x
      • НОД членів цього рівняння дорівнює 2x. винесіть його за дужки:
      • 2x(2x3 + 6x2 + 3x + 9)
  3. Згрупуйте члени рівняння: розгляньте перші два члени (як пару) і другі два члени (теж як пару).
    • Якщо перший член другої пари негативний, то перед дужками другої пари необхідно поставити знак мінус. В цьому випадку змініть знак (в дужках) у другого члена пари на протилежний.
    • Приклад: 2x(2x3 + 6x 2 + 3x + 9) = 2x[(2x3 + 6x 2) +(3x + 9)]
  4. Винесіть за дужки НСД (у кожної пари).
    • У цей момент ви, можливо, зіткнеться з проблемою вибору правильних знаків для другої пари. Подивіться на знаки перед другим і четвертим членами.
      • Якщо обидва знаки однакові (або плюси, або мінуси), то за дужку винесіть позитивне число.
      • Якщо обидва знаки різні (один мінус, а інший плюс), то за дужку винесіть негативне число.
    • Приклад: 2x[(2x3 + 6x 2) +(3x + 9)] = 2x[2x2(x + 3) + 3 (x + 3)]
  5. У двох дужках виходить один і той же вираз.запишіть його як є, а у другі дужки запишіть множники, що стоять за дужками.
    • Якщо вирази в дужках не однакові, Перевірте ваші обчислення або спробуйте згрупувати члени вихідного рівняння по-іншому.
    • Вирази в дужках повинні збігатися. В іншому випадку спосіб угруповання застосовувати не можна.
    • Приклад: 2x[2x2 (x + 3) + 3(x + 3)] = 2x[(x + 3) (2x2 + 3)]
  6. Запишіть відповідь.
    • Приклад: 4x4 + 12x3 + 6x 2 + 18x = 2x(x + 3)(2x2 + 3)
      • Відповідь: 2x(x + 3)(2x2 + 3)

Додаткові приклади

  1. Розкладіть на множники 6x2 + 2XY-24x-8y
    • 2[3x2 + xy - 12x - 4y]
    • 2[(3x2 + xy) - (12x + 4y)]
    • 2[x(3x + y) - 4(3x + y)]
    • 2[(3x + y)(x - 4)]
    • 2(3x + y)(x – 4)
  2. Розкладіть на множники x3 - 2x2 + 5X - 10
    • (x3 - 2x2) + (5x - 10)
    • X2(x - 2) + 5(x - 2)
    • (x - 2)(x2 + 5)

Джерела

  1. ↑ Http://www.mathwarehouse.com/algebra/polynomial/how-to-factor-by-grouping.php
  2. ↑ Http://www.regentsprep.org/Regents/math/algtrig/ATV1/revFactorGrouping.htm
  3. ↑ Http://www.wtamu.edu/academic/anns/mps/math/mathlab/int_algebra/int_alg_tut27_gcf.htm
  4. ↑ Http://www.mesacc.edu/~scotz47781/mat120/notes/factoring/grouping/grouping.html

Ще почитати: