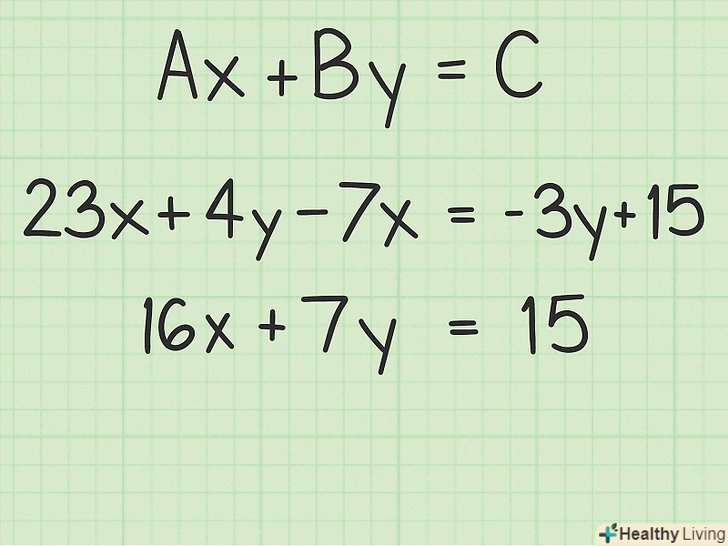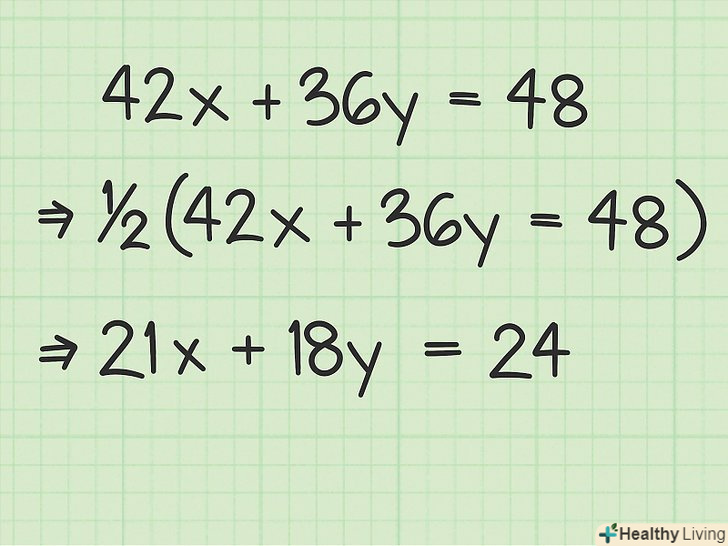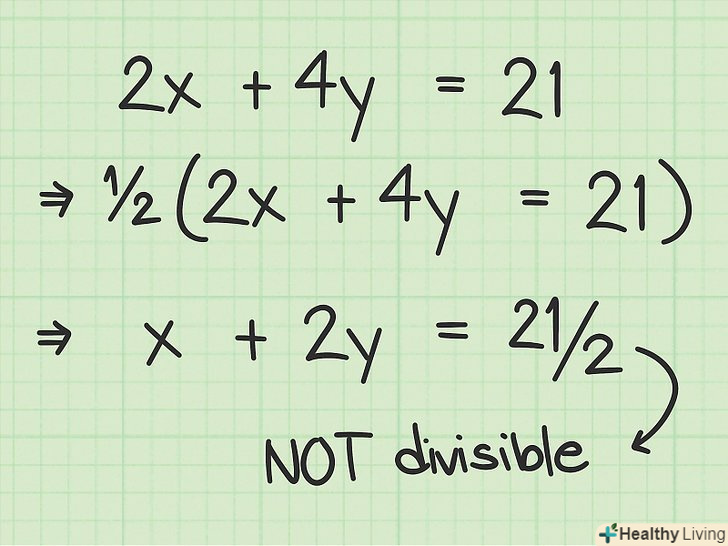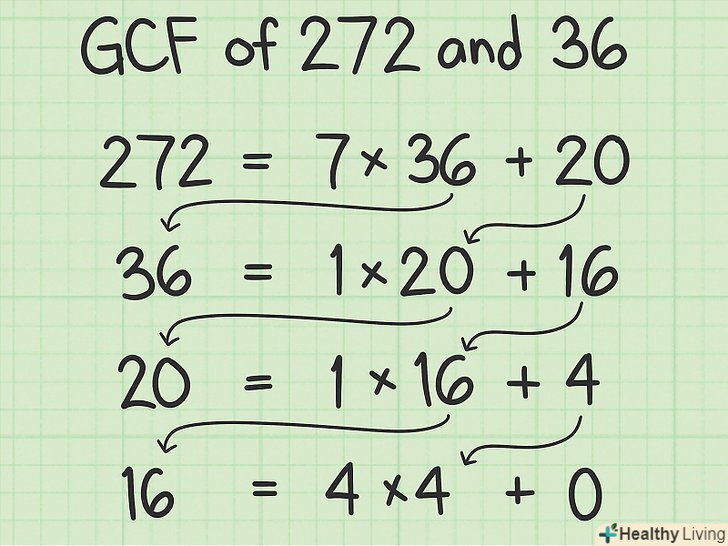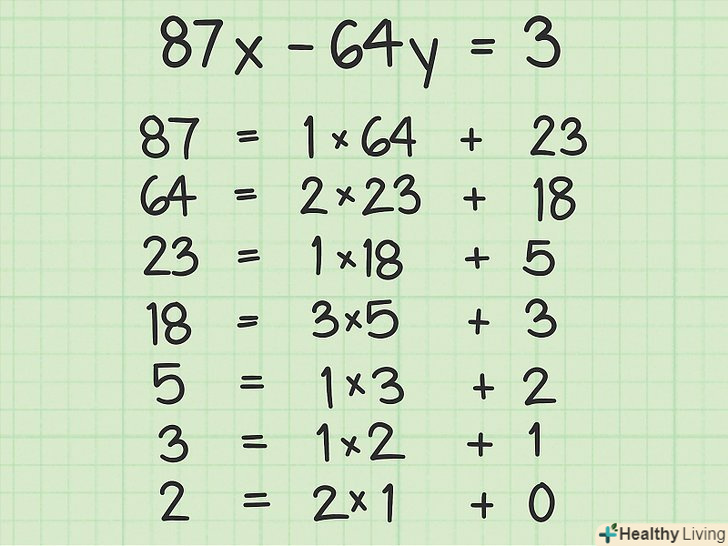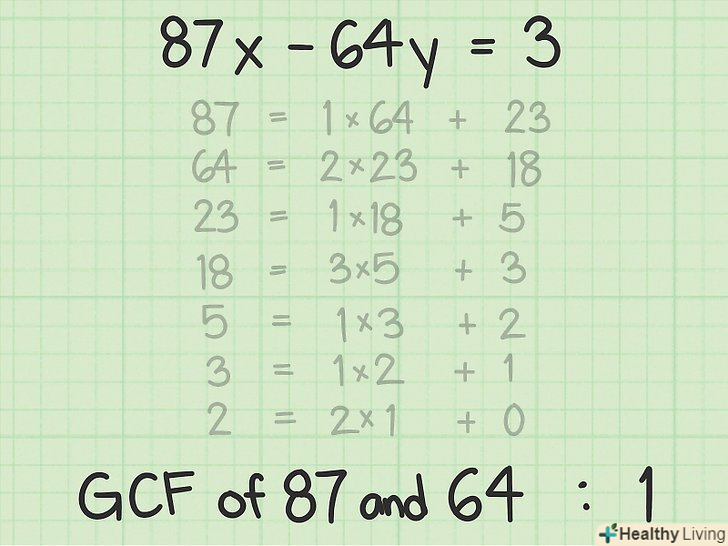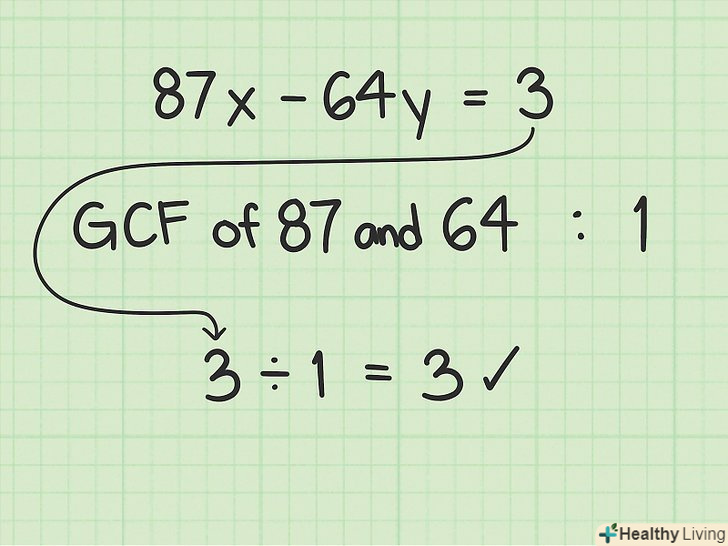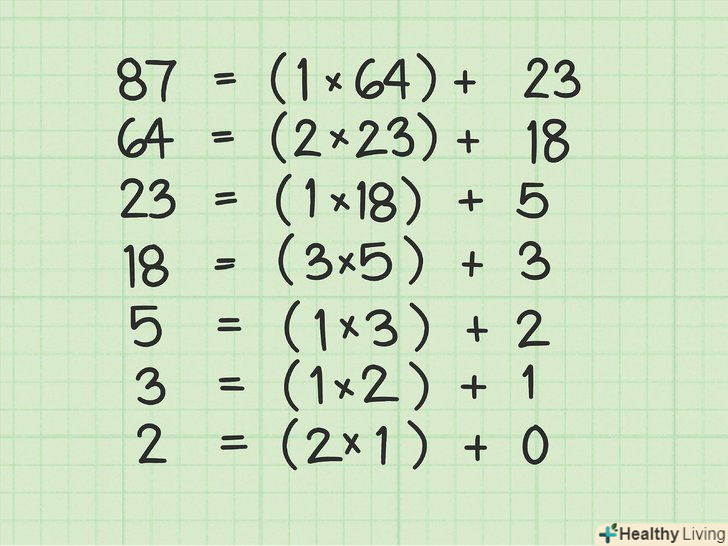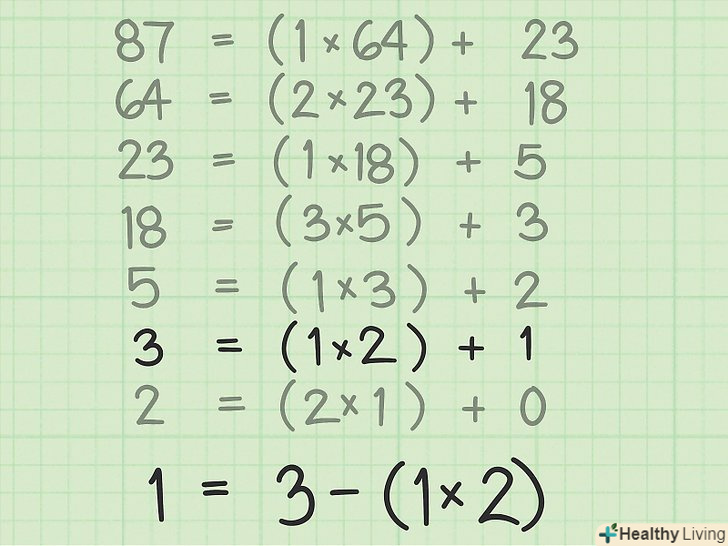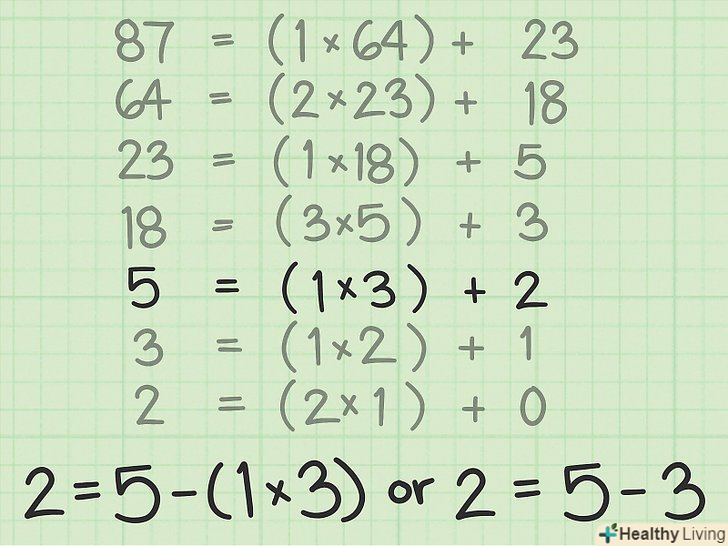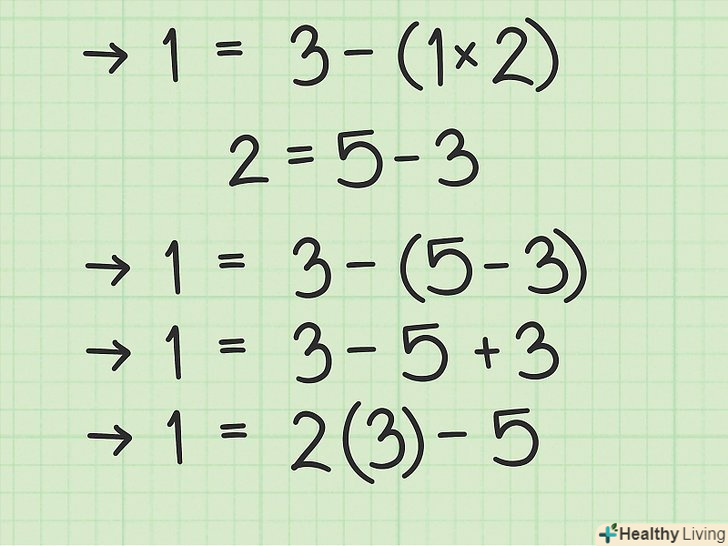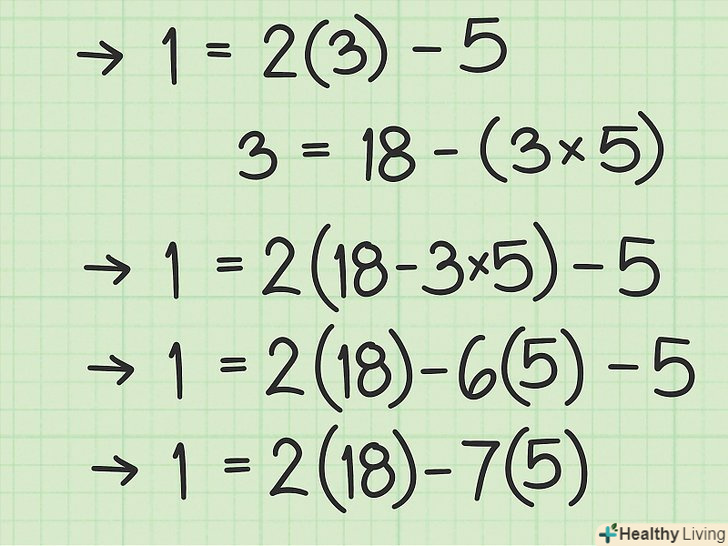1. Головна
    2. Математика
    3. Як розв'язати лінійне діофантове рівняння

Як розв'язати лінійне діофантове рівняння

Щоб вирішити лінійне діофантове рівняння, потрібно знайти значення змінних " x "і» y", які є цілими числами. Цілочисельне рішення складніше звичайного і вимагає певного набору дій. Спочатку необхідно обчислити найбільший спільний дільник (НСД) коефіцієнтів, а потім знайти рішення. Якщо ви знайшли одне цілочисельне рішення лінійного рівняння, можна застосувати простий шаблон, щоб знайти нескінченну безліч інших рішень.

Частина1З 4:
Як записати рівняння

  1. Запишіть рівняння в стандартній формі.лінійне рівняння-це рівняння, в якому показники ступеня змінних не перевищують 1. Щоб вирішити таке лінійне рівняння, спочатку запишіть його в стандартній формі. Стандартна форма лінійного рівняння виглядає так: Ax+By=C{\displaystyle Ax+By=C}, де A,B{\displaystyle A,B} і — цілі числа.
    • Якщо рівняння дано в іншій формі, приведіть його до стандартної форми за допомогою основних алгебраїчних дій. Наприклад, дано рівняння23x+4y−7x=−3y+15{\displaystyle 23x+4y-7x=-3y+15}. Наведіть подібні члени і запишіть рівняння так: 16x+7y=15{\displaystyle 16x+7y=15}.
  2. Спростіть рівняння (якщо можна). Коли ви запишете рівняння в стандартній формі, подивіться на коефіцієнти і C{\displaystyle C}. Якщо у цих коефіцієнтів є НСД, розділіть на нього всі три коефіцієнта. Рішення такого спрощеного рівняння також буде рішенням вихідного рівняння.
    • Наприклад, якщо всі три коефіцієнти парні, розділіть їх як мінімум на 2. Наприклад:
      • (всі члени діляться на 2)
      • (тепер всі члени діляться на 3)
      • (це більше рівняння можна спростити)
  3. Перевірте, чи можна вирішити рівняння.у деяких випадках можна відразу заявити, що рівняння не має рішень. Якщо коефіцієнт "С «не ділиться на НСД коефіцієнтів» а «і» В", у рівняння немає рішень.
    • Наприклад, якщо обидва коефіцієнтиA{\displaystyle A} і парні, то і коефіцієнт має бути парним. Але якщо непарний, то рішення немає.
      • У рівняння2x+4y=21{\displaystyle 2x+4y=21} немає цілочисельних рішень.
      • У рівняння5x+10y=17{\displaystyle 5x+10y=17} немає цілочисельних рішень, так як ліва частина рівняння ділиться на 5, а права — Ні.

Частина2З 4:
Як записати алгоритм Евкліда

  1. Зрозумійте алгоритм Евкліда. це ряд повторних поділок, в якому попередній залишок використовується як наступний дільник. Останній дільник, який ділить числа, є найбільшим спільним дільником (НСД) двох чисел.[1]
    • Наприклад, знайдемо НСД чисел 272 і 36 за допомогою алгоритму Евкліда:
      • — розділіть більше число (272) на менше (36) і зверніть увагу на залишок (20);
      • — розділіть попередній дільник (36) на попередній залишок (20). Зверніть увагу на новий залишок (16);
      • — розділіть попередній дільник (20) на попередній залишок (16). Зверніть увагу на новий залишок (4);
      • — розділіть попередній дільник (16) на попередній залишок (4). Так як залишок дорівнює 0, можна сказати, що 4 є НОДом вихідних двох чисел 272 і 36.
  2. Застосуйте алгоритм Евкліда до коефіцієнтів «A» і «B». коли ви запишете лінійне рівняння в стандартній формі, визначте коефіцієнти "A» і "B", а потім застосуєте до них алгоритм Евкліда, щоб знайти НСД. Наприклад, дано лінійне рівняння 87x−64y=3{\displaystyle 87x-64y=3}.[2]
    • Ось алгоритм Евкліда для коефіцієнтів а=87 і в=64:
  3. Знайдіть найбільший спільний дільник (НСД).оскільки останнім дільником було число 1, НСД 87 і 64 дорівнює 1. Таким чином, 87 і 64 є простими числами по відношенню один до одного.[3]
  4. Проаналізуйте отриманий результат. коли ви знайдете нод коефіцієнтів A{\displaystyle A} і , порівняйте його з коефіцієнтом вихідного рівняння. Якщо C{\displaystyle C} ділиться на НОД і , рівняння має цілочисельне рішення; в іншому випадку у рівняння немає рішень.[4]
    • Наприклад, рівняння87x−64y=3{\displaystyle 87x-64y=3} можна вирішити, тому що 3 ділиться на 1 (НОД=1).
    • Наприклад, припустимо, що НСД=5. 3 не ділиться на 5, тому таке рівняння не має цілочисельних розв'язків.
    • Як показано нижче, якщо рівняння має одне цілочисельне рішення, воно також має нескінченну безліч інших цілочисельних рішень.

Частина3З 4:
Як знайти рішення за допомогою алгоритму Евкліда

  1. Пронумеруйте кроки обчислення НСД.щоб знайти рішення лінійного рівняння, потрібно використовувати алгоритм Евкліда в якості основи процесу підстановки і спрощення.[5]
    • Почніть з нумерації кроків обчислення НСД. Процес обчислення виглядає так:
      • Крок 4:18=(3∗5)+3{\displaystyle {\text{Крок 4}}:18=(3*5)+3}
  2. Зверніть увагу на останній крок, де є залишок.перепишіть рівняння цього кроку так, щоб ізолювати залишок.[6]
    • У нашому прикладі останній крок із залишком-це Крок 6. Залишок дорівнює 1. Перепишіть рівняння кроку 6 наступним чином:
  3. Ізолюйте залишок попереднього кроку. Цей процес являє собою покрокове переміщення вгору». Кожного разу ви будете ізолювати залишок у рівнянні попереднього кроку.[7]
    • Ізолюйте залишок рівняння кроку 5:
      • або
  4. Зробіть заміну і спростіть.зверніть увагу, що рівняння кроку 6 містить число 2, а в рівнянні кроку 5 число 2 ізольоване. Тому замість «2» в рівнянні кроку 6 підставте вираз кроку 5:[8]
    • (рівняння кроку 6)
    • (замість 2 підставили вираз)
    • (розкрили дужки)
    • (спростили)
  5. Повторіть процес підстановки та спрощення.повторіть описаний процес, переміщаючись по алгоритму Евкліда в зворотному порядку. Кожен раз ви будете переписувати рівняння попереднього кроку і підставляти його в останнє отримане рівняння.[9]
    • Останнім розглянутим кроком був Крок 5. Тому перейдіть до кроку 4 і ізолюйте залишок у рівнянні цього кроку:
    • Підставте цей вираз замість " 3 " в останнє рівняння:
  6. Продовжуйте процес підстановки та спрощення.цей процес буде повторюватися до тих пір, поки ви не досягнете початкового кроку алгоритму Евкліда. Мета процесу-записати рівняння з коефіцієнтами 87 і 64 вихідного рівняння, яке потрібно вирішити. У нашому прикладі:[10]
    • (підставили вираз з кроку 3)
    • (підставили вираз з кроку 2)
    • (підставили вираз з кроку 1)

Ще почитати: