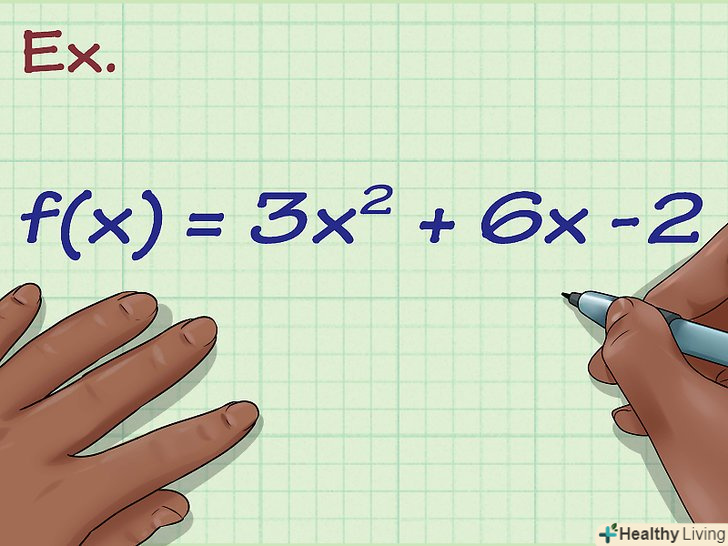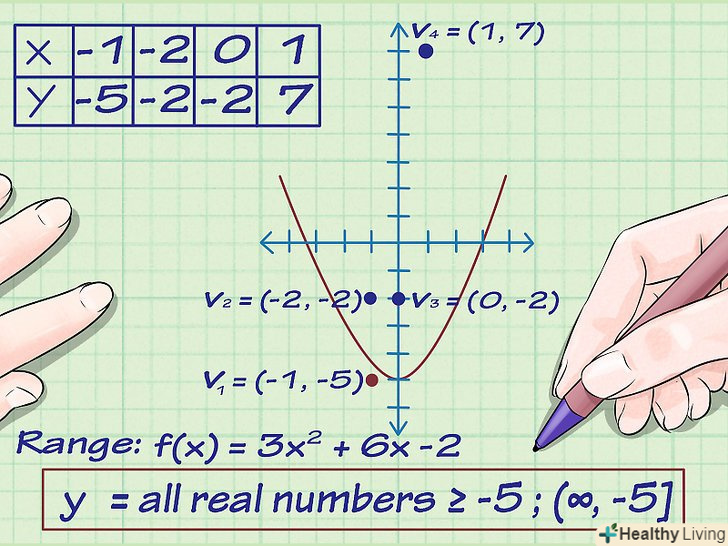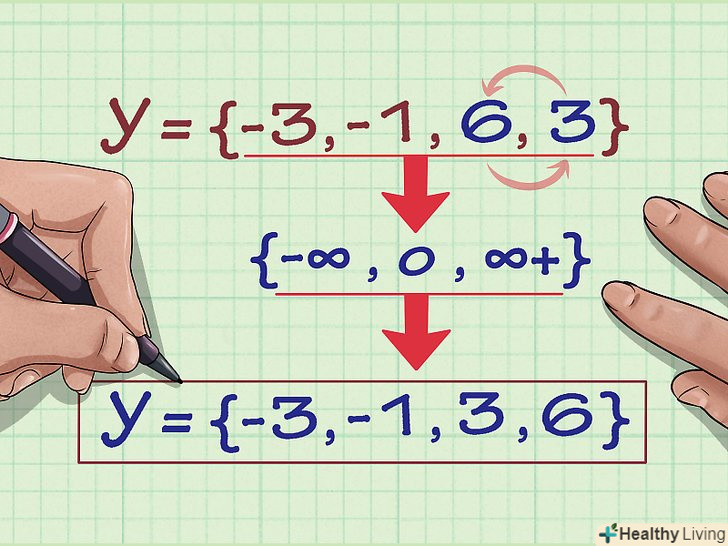Безліч значень (область значень) функції - всі значення, які приймає функція в її області визначення. Іншими словами, це ті значення у, які ви отримуєте при підстановці всіх можливих значень Х.всі можливі значення х і називаються областю визначення функції. Виконайте наступні дії для знаходження безлічі значень функції.
Кроки
Метод1З 4:
Пошук множини значень функції за формулою
Метод1З 4:
 Запишіть функцію. наприклад: f(x) = 3x2 + 6x -2. Підставивши x в рівняння, ми зможемо знайти значення y. ця квадратична функція, і її графік-парабола.
Запишіть функцію. наприклад: f(x) = 3x2 + 6x -2. Підставивши x в рівняння, ми зможемо знайти значення y. ця квадратична функція, і її графік-парабола. Знайдіть вершину параболи. якщо вам дано лінійну функцію або будь-яку іншу зі змінною непарною мірою, наприклад, f(x) = 6X3 + 2x + 7, пропустіть цей крок. Але якщо вам дана квадратична функція або будь-яка інша зі змінною х в парній мірі, потрібно знайти вершину графіка цієї функції. Для цього використовуйте формулу х= - b/2a. У функції 3x2 + 6x -2 a = 3, b = 6, c = -2. Обчислюємо: х = -6/(2*3)= -1.
Знайдіть вершину параболи. якщо вам дано лінійну функцію або будь-яку іншу зі змінною непарною мірою, наприклад, f(x) = 6X3 + 2x + 7, пропустіть цей крок. Але якщо вам дана квадратична функція або будь-яка інша зі змінною х в парній мірі, потрібно знайти вершину графіка цієї функції. Для цього використовуйте формулу х= - b/2a. У функції 3x2 + 6x -2 a = 3, b = 6, c = -2. Обчислюємо: х = -6/(2*3)= -1.- Тепер підставте х= -1 в функцію, щоб знайти у. f(-1) = 3*(-1)2 + 6*(-1) -2 = 3 - 6 -2 = -5.
- Координати вершини параболи (-1,-5). Нанесіть її на координатну площину. Точка лежить в третьому квадранті координатної площини.
 Знайдіть ще кілька точок на графіку. для цього підставте в функцію кілька інших значень х.Так як член x2 позитивний, то парабола буде спрямована вгору. Для підстраховки підставимо в функцію кілька значень x, щоб дізнатися, які значення y вони дають.
Знайдіть ще кілька точок на графіку. для цього підставте в функцію кілька інших значень х.Так як член x2 позитивний, то парабола буде спрямована вгору. Для підстраховки підставимо в функцію кілька значень x, щоб дізнатися, які значення y вони дають.- F(-2) = 3(-2)2 + 6(-2) -2 = -2. перша точка на параболі (-2, -2)
- F(0) = 3(0)2 + 6(0) -2 = -2. Друга точка на параболі (0,-2)
- F(1) = 3(1)2 + 6(1) -2 = 7. Третя точка на параболі (1, 7).
 Знайдіть безліч значень функції на графіку. знайдіть найменше значення у на графіку. Ця вершина параболи, де у=-5. Так як парабола лежить вище вершини, то безліч значень функції y ≥ -5.
Знайдіть безліч значень функції на графіку. знайдіть найменше значення у на графіку. Ця вершина параболи, де у=-5. Так як парабола лежить вище вершини, то безліч значень функції y ≥ -5.
Метод2З 4:
Пошук безлічі значень функції на графіку
Метод2З 4:
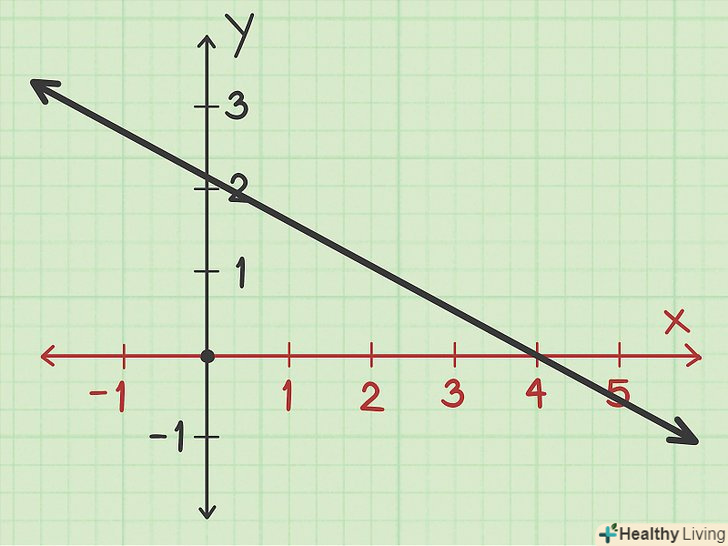
 Знайдіть мінімум функції. обчисліть найменше значення у. припустимо, мінімум функції у=-3. Це значення може ставати все менше і менше, аж до нескінченності, так що мінімум функції не має заданої мінімальної точки.
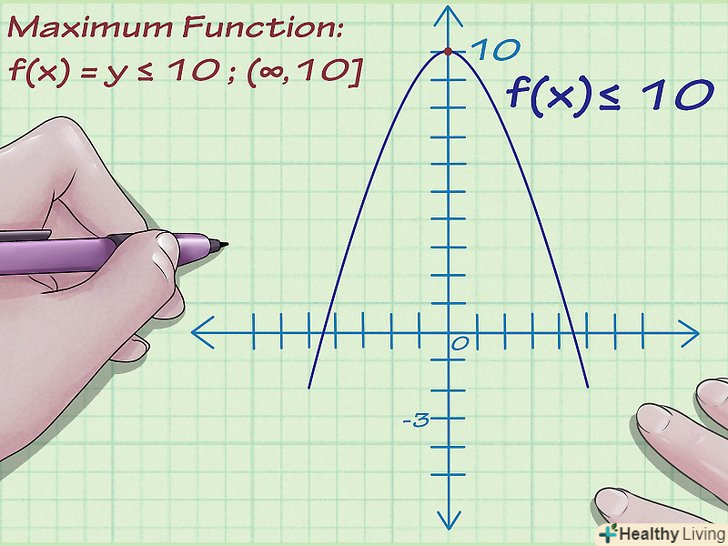
Знайдіть мінімум функції. обчисліть найменше значення у. припустимо, мінімум функції у=-3. Це значення може ставати все менше і менше, аж до нескінченності, так що мінімум функції не має заданої мінімальної точки. Знайдіть максимум функції.припустимо, максимум функції у= 10. Як і у випадку з мінімумом, максимум функції не має заданої максимальної точки.
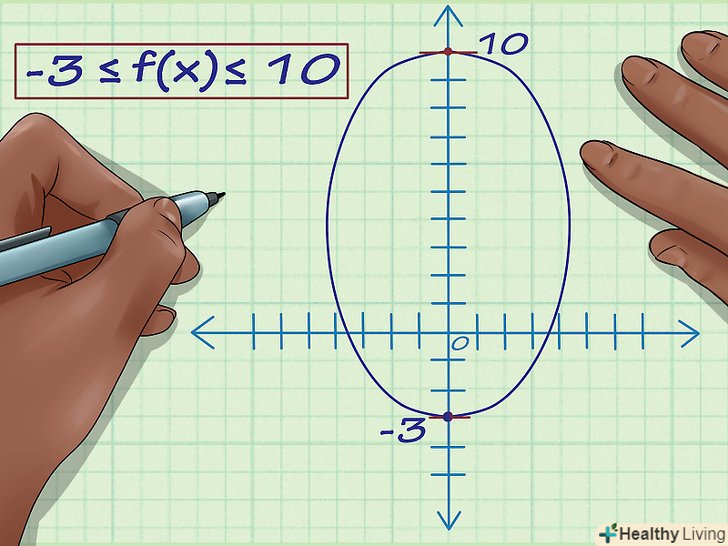
Знайдіть максимум функції.припустимо, максимум функції у= 10. Як і у випадку з мінімумом, максимум функції не має заданої максимальної точки. Запишіть безліч значень.таким чином, безліч значень функції лежить в діапазоні від -3 до +10. Запишіть безліч значень функції як: -3 ≤ f (x) ≤ 10
Запишіть безліч значень.таким чином, безліч значень функції лежить в діапазоні від -3 до +10. Запишіть безліч значень функції як: -3 ≤ f (x) ≤ 10- Але, припустимо, мінімум функції у=-3, а її максимум — нескінченність (графік функції йде нескінченно вгору). Тоді безліч значень функції: f (x) ≥ -3.
- З іншого боку, якщо максимум функції у=10, а мінімум-нескінченність(графік функції йде нескінченно вниз), то безліч значень функції: f (x) ≤ 10.
Метод3З 4:
Пошук області значень множини координат
Метод3З 4:
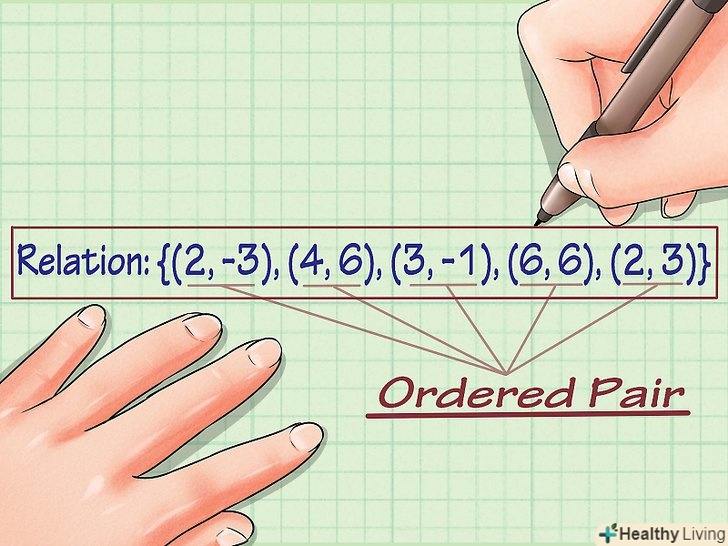
 Запишіть безліч координат.з безлічі координат можна визначити його область значення і область визначення. Припустимо, дано безліч координат: {(2, -3), (4, 6), (3, -1), (6, 6), (2, 3)}.[1]
Запишіть безліч координат.з безлічі координат можна визначити його область значення і область визначення. Припустимо, дано безліч координат: {(2, -3), (4, 6), (3, -1), (6, 6), (2, 3)}.[1] Перерахуйте значення у. щоб знайти область значень множини, просто запишіть всі значення у: {-3, 6, -1, 6, 3}.[2]
Перерахуйте значення у. щоб знайти область значень множини, просто запишіть всі значення у: {-3, 6, -1, 6, 3}.[2] Видаліть всі повторювані значення у. у нашому прикладі видаліть "6": {-3, -1, 6, 3}.[3]
Видаліть всі повторювані значення у. у нашому прикладі видаліть "6": {-3, -1, 6, 3}.[3] Запишіть область значень у порядку зростання.областю значень множини координат {(2, -3), (4, 6), (3, -1), (6, 6), (2, 3)} буде {-3, -1, 3, 6}.[4]
Запишіть область значень у порядку зростання.областю значень множини координат {(2, -3), (4, 6), (3, -1), (6, 6), (2, 3)} буде {-3, -1, 3, 6}.[4] Переконайтеся, що багато координат дано для функції. щоб це було так, кожному одному значенню х має відповідати одне значення у. Наприклад, безліч координат {(2, 3) (2, 4) (6, 9)} дано не для функції, тому що одному значенню х=2 відповідають два різних значення у: у=3 і у=4.[5]
Переконайтеся, що багато координат дано для функції. щоб це було так, кожному одному значенню х має відповідати одне значення у. Наприклад, безліч координат {(2, 3) (2, 4) (6, 9)} дано не для функції, тому що одному значенню х=2 відповідають два різних значення у: у=3 і у=4.[5]
Метод4З 4:
Пошук області значень у задачах
Метод4З 4:
 Прочитайте завдання."Ольга продає квитки в театр по 500 рублів за квиток. Загальна виручена сума за продані Квитки є функцією від кількості проданих квитків. Яка область значень цієї функції?»
Прочитайте завдання."Ольга продає квитки в театр по 500 рублів за квиток. Загальна виручена сума за продані Квитки є функцією від кількості проданих квитків. Яка область значень цієї функції?» Запишіть завдання як функцію. в цьому випадку М — загальна виручена сума за продані квитки, а t — кількість проданих квитків. Так як один квиток коштує 500 рублів, треба помножити кількість проданих квитків на 500, щоб знайти виручену суму. Таким чином, функція може бути записана у вигляді M(t) = 500T.
Запишіть завдання як функцію. в цьому випадку М — загальна виручена сума за продані квитки, а t — кількість проданих квитків. Так як один квиток коштує 500 рублів, треба помножити кількість проданих квитків на 500, щоб знайти виручену суму. Таким чином, функція може бути записана у вигляді M(t) = 500T.- Наприклад, якщо вона продасть 2 квитка, потрібно помножити 2 на 500 — в результаті отримаємо 1000 рублів, виручених за продані Квитки.
 Знайдіть область визначення.для знаходження області значень ви повинні спочатку знайти область визначення. Це всі можливі значення t. у нашому прикладі Ольга може продати 0 або більше квитків, - вона не може продати негативне число квитків. Оскільки ми не знаємо Кількість місць в театрі, можна припустити, що теоретично вона може продати нескінченне число квитків. І вона може продавати тільки цілі квитки (вона не може продати, наприклад, 1/2 квитка). Таким чином, область визначення функції t = будь-яке невід'ємне ціле число.
Знайдіть область визначення.для знаходження області значень ви повинні спочатку знайти область визначення. Це всі можливі значення t. у нашому прикладі Ольга може продати 0 або більше квитків, - вона не може продати негативне число квитків. Оскільки ми не знаємо Кількість місць в театрі, можна припустити, що теоретично вона може продати нескінченне число квитків. І вона може продавати тільки цілі квитки (вона не може продати, наприклад, 1/2 квитка). Таким чином, область визначення функції t = будь-яке невід'ємне ціле число. Знайдіть область значень.це можлива кількість грошей, які Ольга виручить від продажу квитків. Якщо ви знаєте, що область визначення функції - будь-яке невід'ємне ціле число, а функція має вигляд: М(t) = 5T, то ви можете знайти виручену суму, підставивши в функцію будь невід'ємне ціле число (замість t). Наприклад, якщо вона продасть 5 квитків, то М(5) = 5*500 = 2500 рублів. Якщо вона продасть 100 квитків, то М(100) = 500 х 100 = 50000 рублів. Таким чином, область значень функції - будь-які невід'ємні цілі числа, кратні п'ятистам.
Знайдіть область значень.це можлива кількість грошей, які Ольга виручить від продажу квитків. Якщо ви знаєте, що область визначення функції - будь-яке невід'ємне ціле число, а функція має вигляд: М(t) = 5T, то ви можете знайти виручену суму, підставивши в функцію будь невід'ємне ціле число (замість t). Наприклад, якщо вона продасть 5 квитків, то М(5) = 5*500 = 2500 рублів. Якщо вона продасть 100 квитків, то М(100) = 500 х 100 = 50000 рублів. Таким чином, область значень функції - будь-які невід'ємні цілі числа, кратні п'ятистам.- Це означає, що будь-яке невід'ємне ціле число, яке ділиться на 500, є значенням у (виручена сума) нашої функції.
Поради
- У більш складних випадках краще спочатку креслити графік, використовуючи область визначення, і тільки потім знаходити область значень.
- Подивіться, чи можете ви знайтизворотну функцію. Область визначення зворотної функції дорівнює області значень вихідної функції.
- Перевірте, чи функція повторюється. Будь-яка функція, яка повторюється вздовж осі x, матиме ту ж область значень для всієї функції. Наприклад, область значень для f(x) = sin (x) становитиме від -1 до 1.