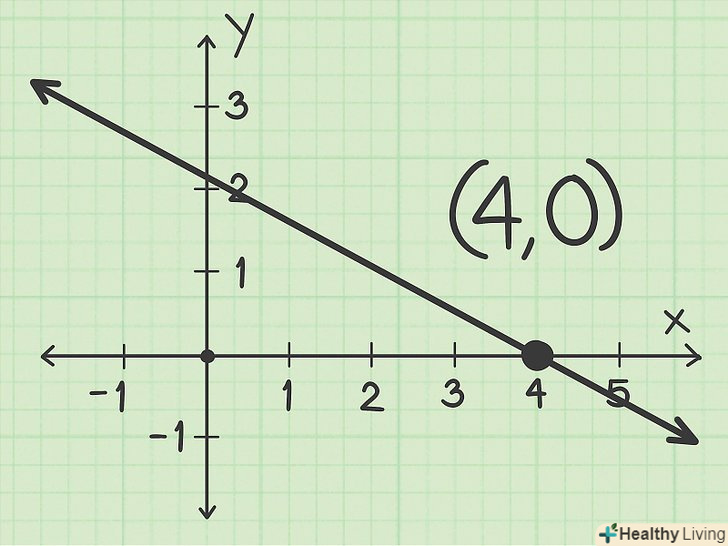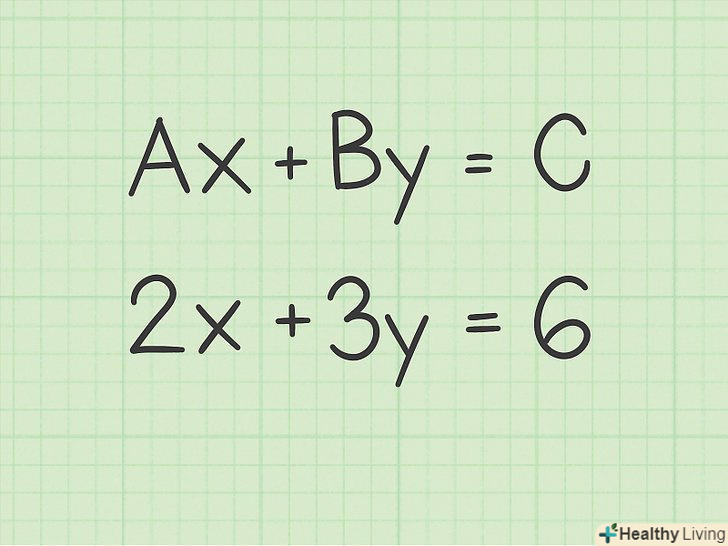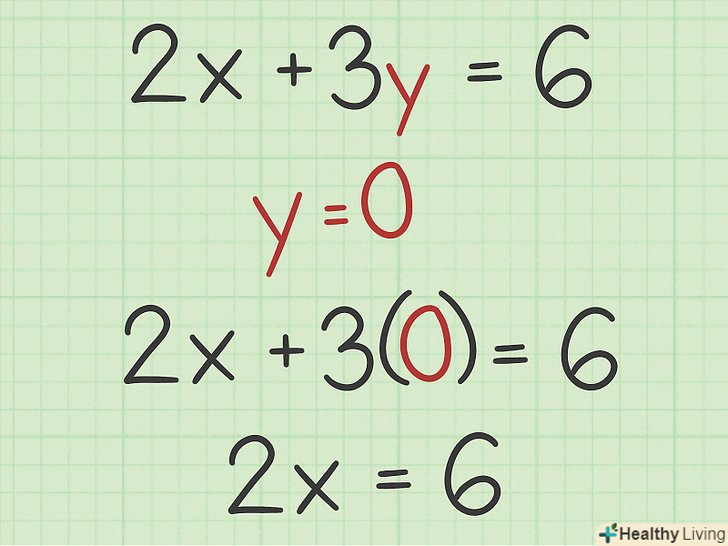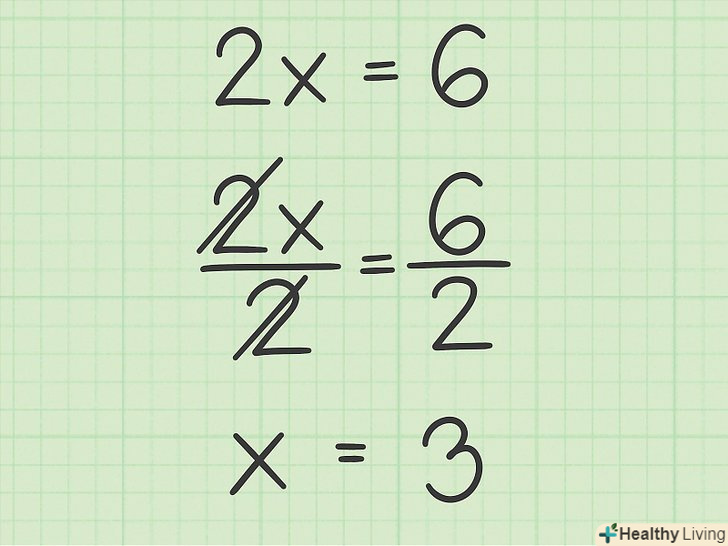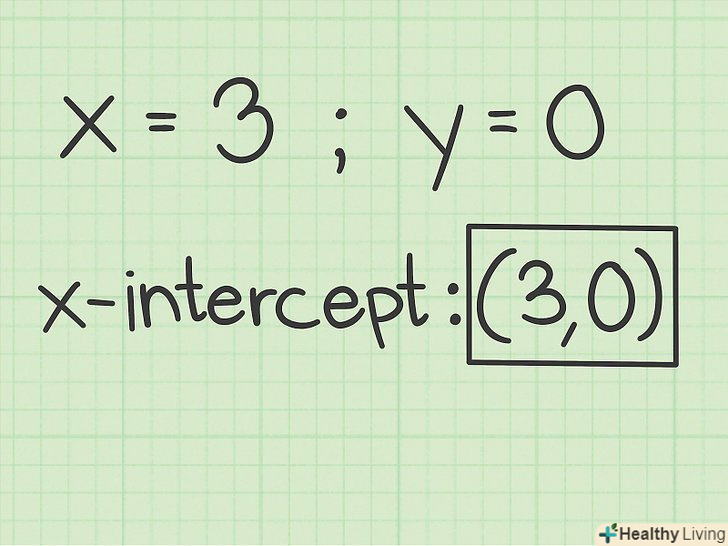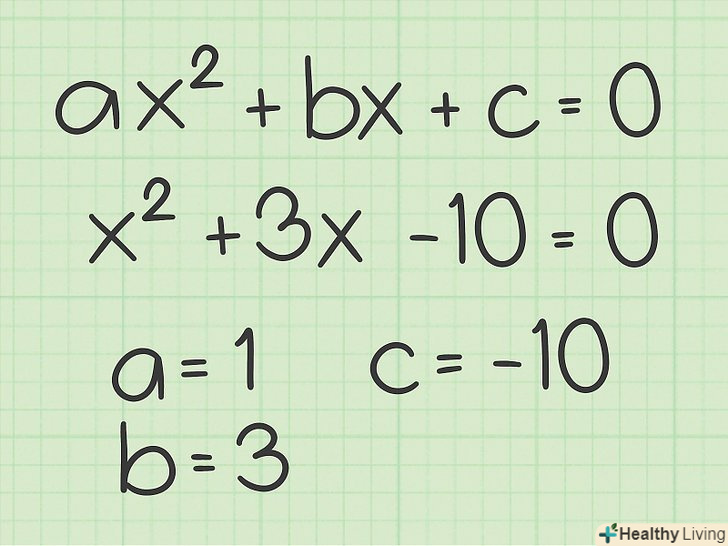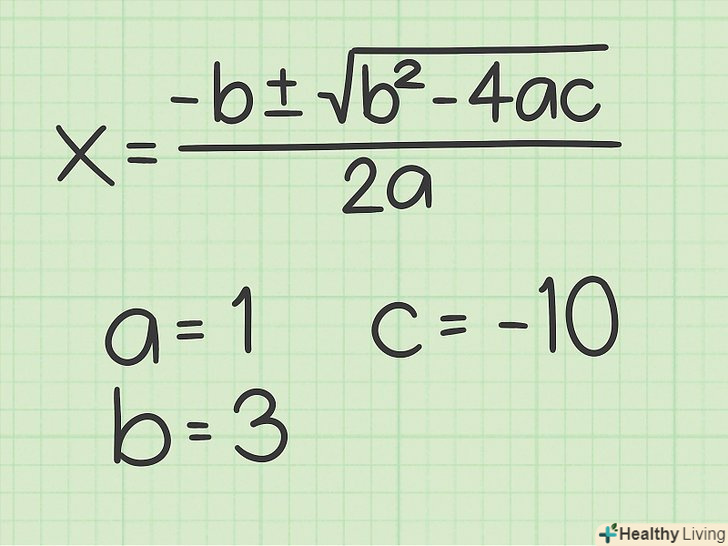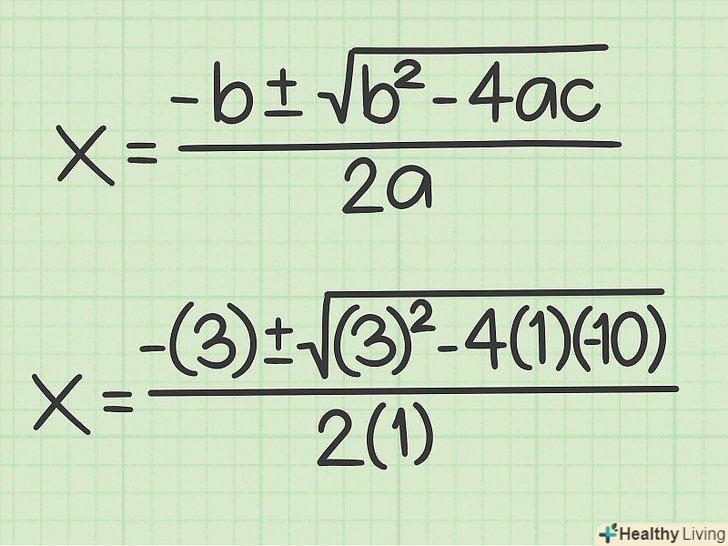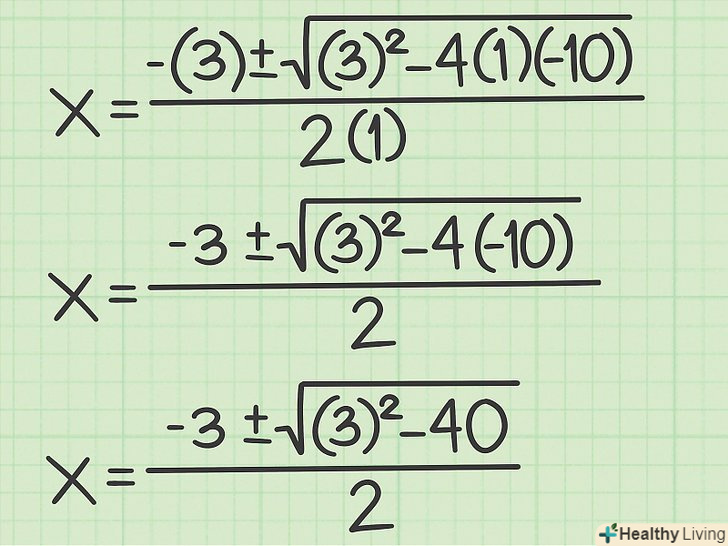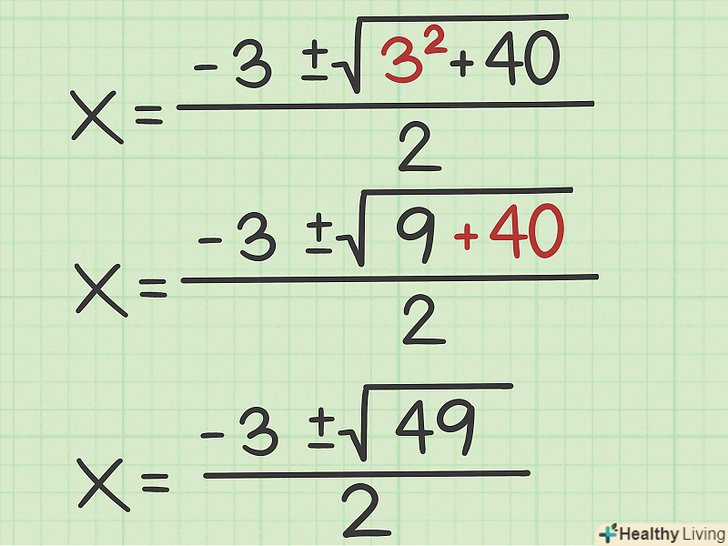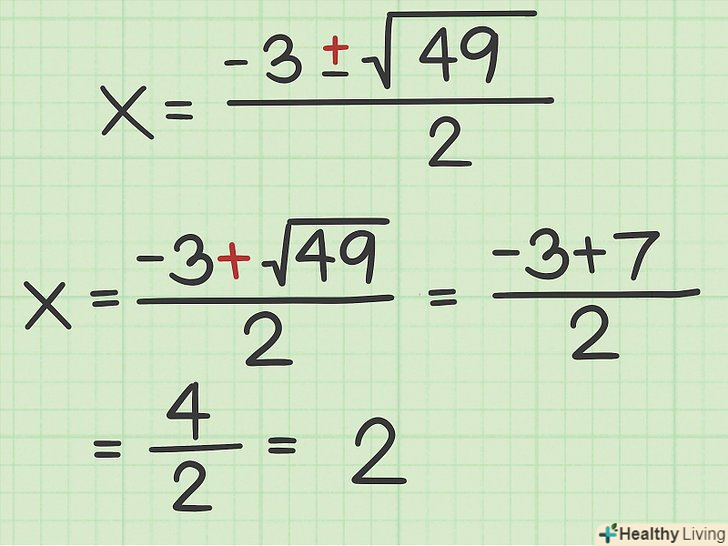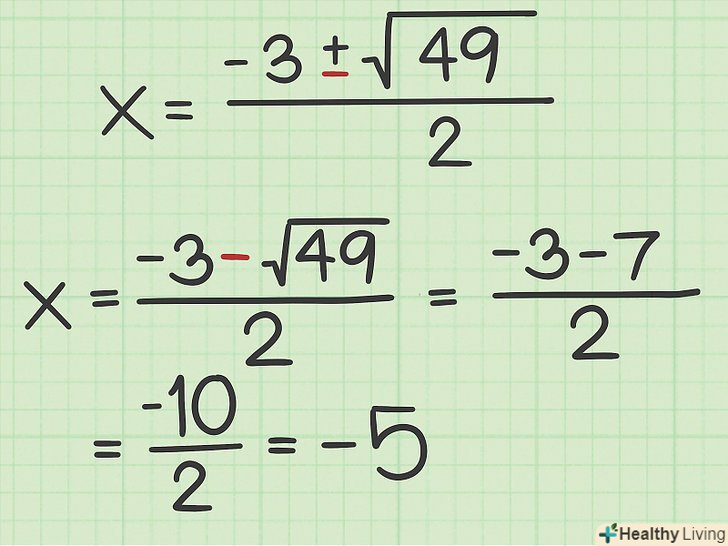В алгебрі прямокутну систему координат на площині утворюють дві взаємно перпендикулярні осі-вісь Х (горизонтальна вісь) і вісь Y (вертикальна вісь). Точки перетину-це точки, в яких графіки функцій перетинають осі координат. Точка перетину з віссю Y і точка перетину з віссю X лежать на відповідних осях. У простих завданнях точку перетину з віссю Х легко знайти за графіком функції. Також цю точку перетину можна обчислити за допомогою рівняння функції.
Кроки
Метод1З 3:
Використання графіка функції
Метод1З 3:
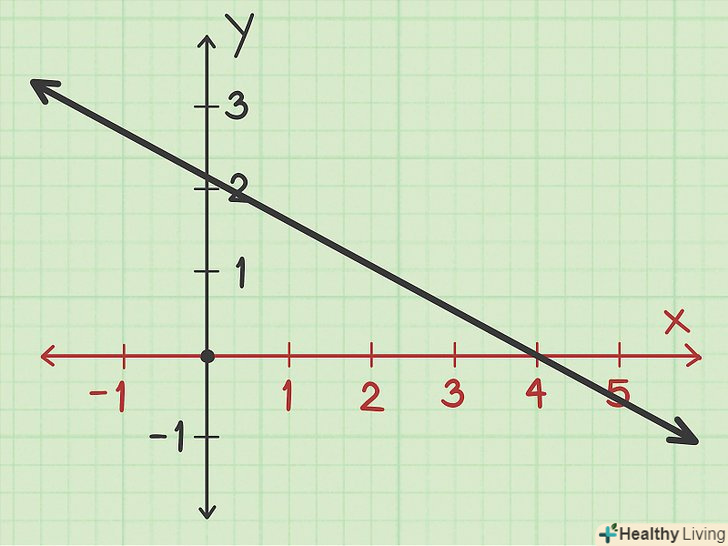
 Знайдіть вісь Х. прямокутна система координат утворюється двома осями – віссю Х (горизонтальна вісь, яка спрямована зліва направо) і віссю Y (вертикальна вісь, яка спрямована знизу вгору).[1] щоб знайти точку перетину з віссю Х, подивіться на цю вісь.
Знайдіть вісь Х. прямокутна система координат утворюється двома осями – віссю Х (горизонтальна вісь, яка спрямована зліва направо) і віссю Y (вертикальна вісь, яка спрямована знизу вгору).[1] щоб знайти точку перетину з віссю Х, подивіться на цю вісь. Знайдіть точку, в якій графік перетинає вісь Х. це точка перетину графіка з віссю х.[2] якщо потрібно знайти точку перетину з віссю Х за графіком, можливо, координатою
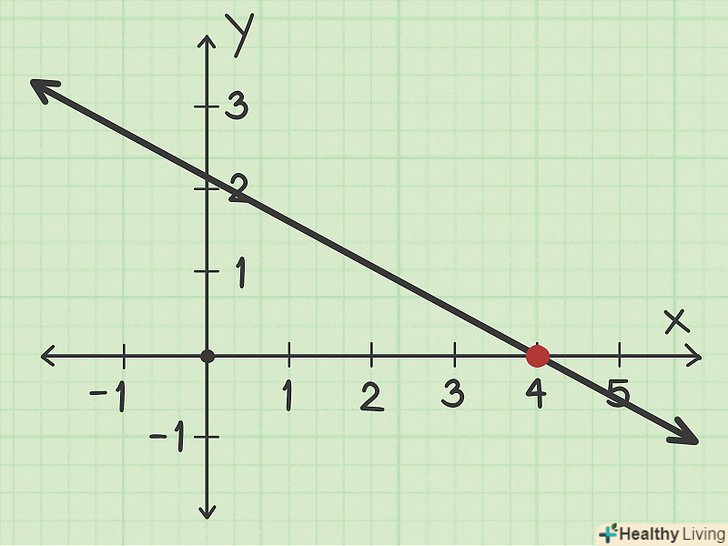
Знайдіть точку, в якій графік перетинає вісь Х. це точка перетину графіка з віссю х.[2] якщо потрібно знайти точку перетину з віссю Х за графіком, можливо, координатоюцієї точки буде ціле число, наприклад, 4. Однак у більшості випадків за графіком вдасться визначити лише приблизну координату
, наприклад, між 4 і 5.
 Запишіть координати точки перетину з віссю х. координати точки записуються у вигляді пари координат< span class= "mwe-math-mathml-inline mwe-math-mathml-a11y "style=" display: none;" data-original-text="(x,y)">
Запишіть координати точки перетину з віссю х. координати точки записуються у вигляді пари координат< span class= "mwe-math-mathml-inline mwe-math-mathml-a11y "style=" display: none;" data-original-text="(x,y)">.[3] перша координата – це координата
точки перетину з віссю Х; друга координата (координата
) завжди дорівнює 0, так як точка перетину з віссю Х лежить на цій осі.[4]
- Наприклад, якщо координата
точки перетину дорівнює 4, то парою координат точки перетину з віссю Х є координати
.
- Наприклад, якщо координата
Метод2 З 3:
Використання лінійного рівняння
Метод2 З 3:
 Визначте, чи записано рівняння у вигляді лінійного діофантового рівняння. таке рівняння має вигляд
Визначте, чи записано рівняння у вигляді лінійного діофантового рівняння. таке рівняння має вигляд,[5], де
,
,
– цілі числа,
і
– координати точки, яка лежить на прямій (графік лінійного рівняння).
- Наприклад, дано рівняння
.
- Наприклад, дано рівняння
 Замість
Замістьпідставте 0. Точка перетину з віссю Х є точкою, в якій пряма перетинає цю вісь.[6] Координата
точки перетину прямої з віссю Х завжди дорівнює 0.[7] таким чином, щоб знайти точку перетину з віссю Х, потрібно замість
підставити 0 і знайти значення
.
- У нашому прикладі, якщо замість
підставити 0, рівняння запишеться наступним чином:
; це рівняння спрощується до
.
- У нашому прикладі, якщо замість
 Знайдіть значення
Знайдіть значення. для цього потрібно ізолювати змінну
, розділивши обидві частини рівняння на коефіцієнт при цієї змінної. Ви знайдете Значення
за
, тобто координату
точки перетину з віссю Х.
- Наприклад:
- Наприклад:
 Запишіть координати точки перетину з віссю Х. Координати точки записуються у вигляді пари координат
Запишіть координати точки перетину з віссю Х. Координати точки записуються у вигляді пари координат. Перша координата – це координата
, значення якої ви тільки що знайшли, а друга координата (координата
) завжди дорівнює 0, так як точка перетину з віссю Х лежить на цій осі.[8]
- Наприклад, графік лінійного рівняння
перетинає вісь Ох у точці з координатами
.
- Наприклад, графік лінійного рівняння
Метод3 З 3:
Використання формули для вирішення квадратного рівняння
Метод3 З 3:
 Визначте, чи записано рівняння у вигляді квадратного рівняння. квадратне рівняння має вигляд
Визначте, чи записано рівняння у вигляді квадратного рівняння. квадратне рівняння має вигляд.[9] квадратне рівняння має два корені: графік такого рівняння являє собою параболу і перетинає вісь Х в двох точках.[10]
- Наприклад, рівняння
є квадратним рівнянням, тому Графік перетне вісь Х в двох точках.
- Наприклад, рівняння
 Запишіть формулу для вирішення квадратного рівняння. Формула:
Запишіть формулу для вирішення квадратного рівняння. Формула:, де
– коефіцієнт при змінній другого порядку (
),
– коефіцієнт при змінній першого порядку (
),
– вільний член.[11]
 Підставте відповідні значення в формулу для вирішення квадратного рівняння.переконайтеся, що замість кожної змінної підставляєте правильне значення.
Підставте відповідні значення в формулу для вирішення квадратного рівняння.переконайтеся, що замість кожної змінної підставляєте правильне значення.- Наприклад, якщо рівняння має вигляд
, формула запишеться так:
.
- Наприклад, якщо рівняння має вигляд
 Спростіть рівняння.для початку перемножте відповідні значення. Переконайтеся, що врахували всі знаки «плюс» і «мінус».
Спростіть рівняння.для початку перемножте відповідні значення. Переконайтеся, що врахували всі знаки «плюс» і «мінус».- Наприклад:
- Наприклад:
 Зведіть відповідне значення в квадрат. зробіть це зі значенням змінної
Зведіть відповідне значення в квадрат. зробіть це зі значенням змінної. Потім результат додайте до іншого числа, яке знаходиться під знаком кореня.
- Наприклад:
- Наприклад:
 Виконайте додавання. Так як у формулі присутній знак
Виконайте додавання. Так як у формулі присутній знак, доведеться виконати одну операцію додавання і одну операцію віднімання. Виконайте додавання, щоб знайти перше значення
.
- Наприклад:
- Наприклад:
 Виконайте віднімання. так ви знайдете друге значення
Виконайте віднімання. так ви знайдете друге значення. Спочатку витягніть квадратний корінь, потім виконайте віднімання в чисельнику і, нарешті, результат розділіть на 2.
- Наприклад:
- Наприклад:
 Знайдіть пари координат точок перетину параболи з віссю х. Пам'ятайте, що координати точки записуються у вигляді пари координат
Знайдіть пари координат точок перетину параболи з віссю х. Пам'ятайте, що координати точки записуються у вигляді пари координат. Перша координата – це координата
, два значення якої Ви тільки що знайшли (за формулою), а друга координата (координата
) завжди дорівнює 0, так як точка перетину з віссю Х лежить на цій осі.[12]
- Наприклад, графік рівняння
перетинає вісь Х в точках з координатами
і
- Наприклад, графік рівняння