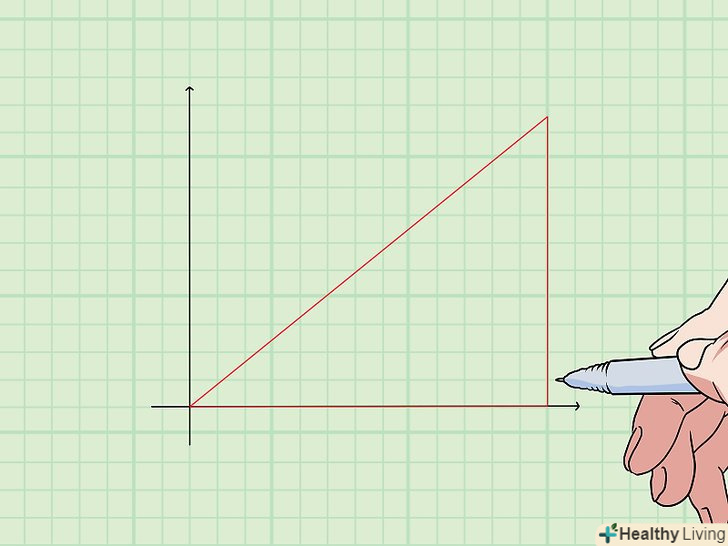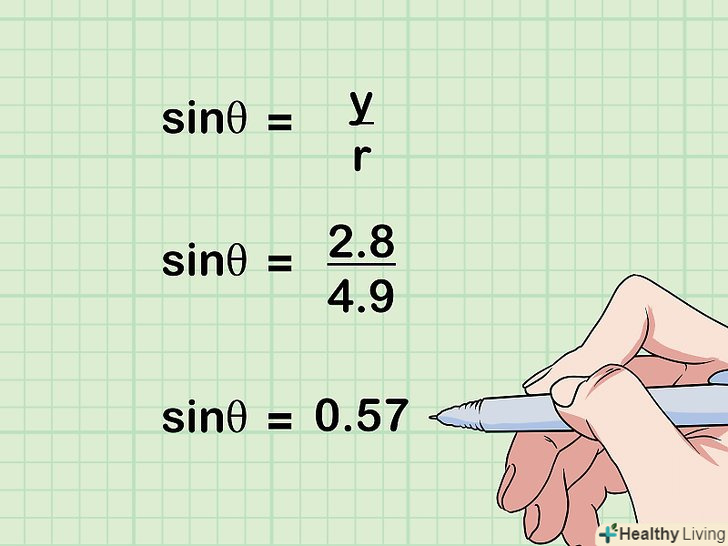1. Головна
    2. Математика
    3. Як запам'ятати таблицю значень тригонометричних функцій

Як запам'ятати таблицю значень тригонометричних функцій

Тригонометрія-це розділ математики, в якому розглядаються сторони і кути трикутників. Найчастіше в тригонометричних задачах потрібно знайти значення тригонометричних функцій, а саме синус, косинус і тангенс кута трикутника. За допомогою спеціальної таблиці або прямокутного трикутника можна швидко обчислити значення тригонометричних функцій найбільш поширених кутів.

Метод1 З 2:
Таблиця

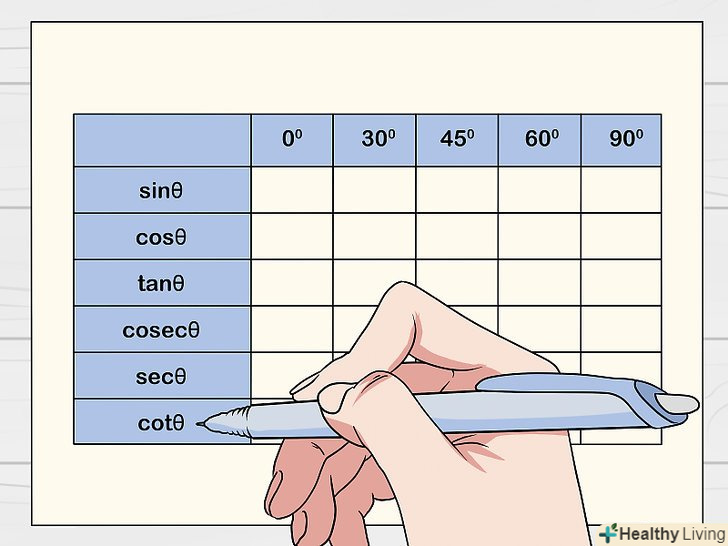
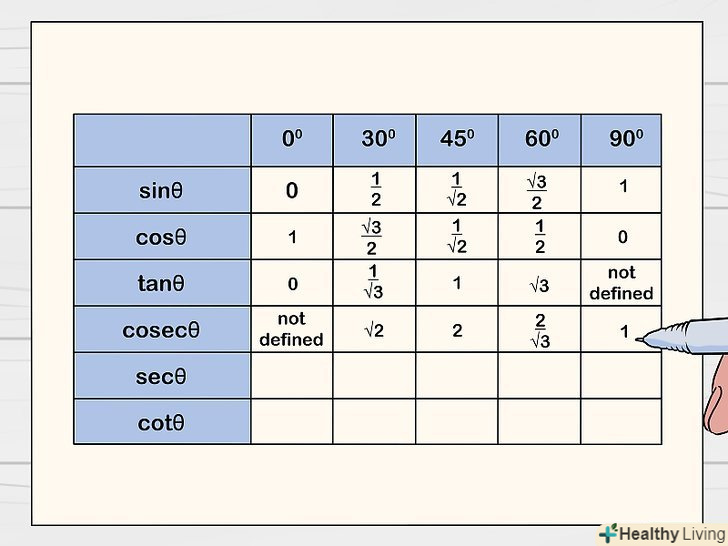
  1. Намалюйте таблицю з 6 рядків і 6 стовпців.у першому стовпці запишіть позначення тригонометричних функцій (sin, cos, tg, cosec, sec і ctg). У першому рядку запишіть величини кутів, які найчастіше зустрічаються в тригонометрії (0°, 30°, 45°, 60°, 90°). Решта комірки таблиці залиште порожніми.[1]
    • Синус (sin), косинус (cos) і тангенс (tg) є найбільш використовуваними тригонометричними функціями, але рекомендуємо також вивчити косеканс (cosec), секанс (sec) і котангенс (ctg), щоб зрозуміти тригонометричну таблицю.
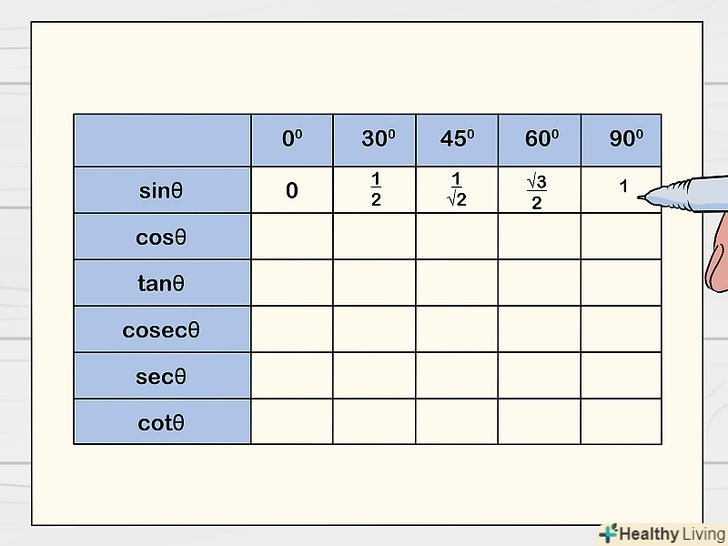
  2. Заповніть порожні клітинки рядка "sin".для цього скористайтеся виразом √x / 2. Замість " x " підставляйте величини кутів, які вказані в першому стовпці таблиці. Використовуйте цей вираз, щоб обчислити значення синуса для кутів 0°, 30°, 45°, 60° і 90°; знайдені значення запишіть в таблицю.[2]
    • Наприклад, щоб заповнити першу комірку (sin 0°) рядка "sin«, у вираз √x/2 замість» x" підставте 0. Ви отримаєте: √0/2 = 0/2 = 0.
    • Якщо в вираз підставляти величини кутів, осередки рядка " sin " заповняться наступним чином:0; √1/2 = 1/2; √2/2 = (√2 х √2)/(2 x √2) = 2/2√2 = 1/√2; √3/2; √4/2 = 2/2 = 1.
    • Коли ви заповните рядок "sin", заповнити залишилися рядки буде простіше.
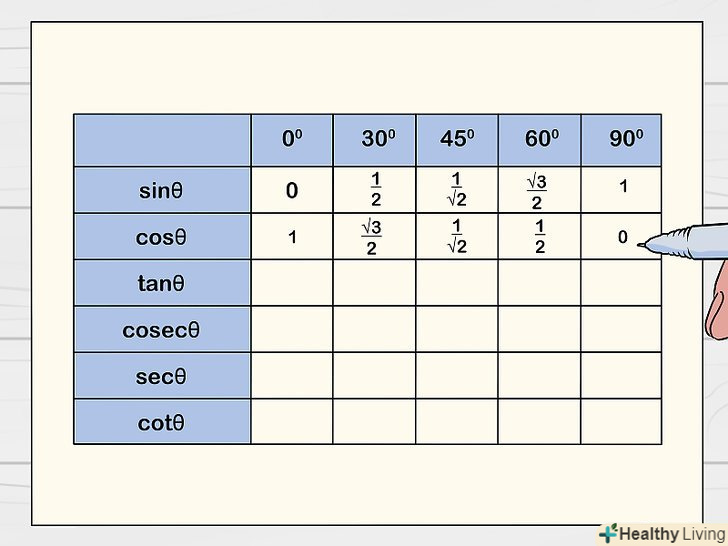
  3. Запишіть значення, які знаходяться в терміні "sin«, в рядку» cos", але в зворотному порядку.це можна зробити, оскільки sin x° = cos (90-x)° для будь-якого значення "x". Таким чином, щоб заповнити рядок "cos«, перенесіть в неї значення з рядка» sin", але в зворотному порядку. Тобто sin 90° = cos 0°, sin 60° = cos 30° і так далі.[3]
    • Наприклад, в останній комірці рядка "sin «знаходиться 1 (sin 90° = 1) — це значення запишіть в першу комірку рядка» cos" (cos 0° = 1).
    • Отже, комірки рядка» cos " заповняться наступним чином:1; √3/2; 1/√2; 1/2; 0.
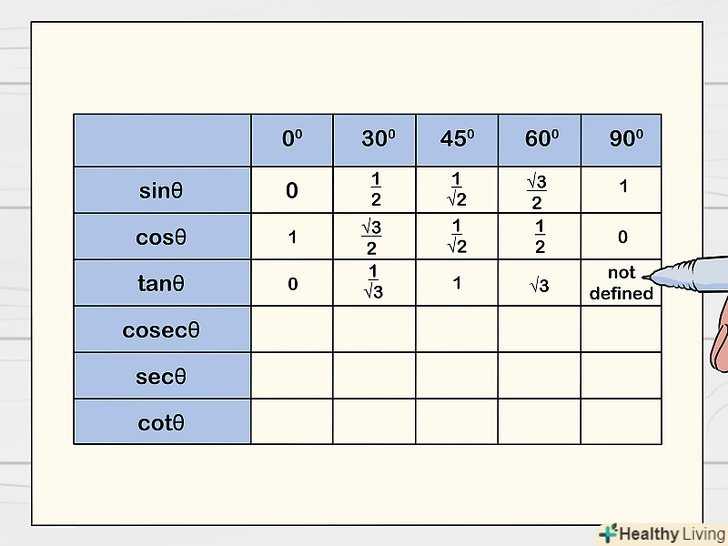
  4. Розділіть значення в рядку "sin «на значення в рядку» cos«, щоб заповнити рядок»tg".це можна зробити, оскільки tg = sin/cos. Таким чином, тангенс кута дорівнює відношенню синуса до косинусу.[4]
    • Наприклад, розглянемо кут 30°: tg 30° = sin 30° / cos 30° = (√1/2)/(√3/2) = 1/√3.
    • Отже, комірки рядка " tg " заповняться наступним чином:0; 1/√3; 1; √3; -. Зверніть увагу, що tg 90° не визначено, тому що sin 90°/cos 90° = 1/0, а на 0 ділити не можна.
  5. Розділіть 1 на значення рядка "sin«, щоб заповнити рядок»cosec".це можна зробити, оскільки cosec = 1 / sin. Наприклад, sin 30° = 1/2, тому cosec 30° = 1/(1/2) = 2.[5]
    • Отже, комірки рядка "cosec" заповняться наступним чином:-; 2; √2; 2/√3; 1.
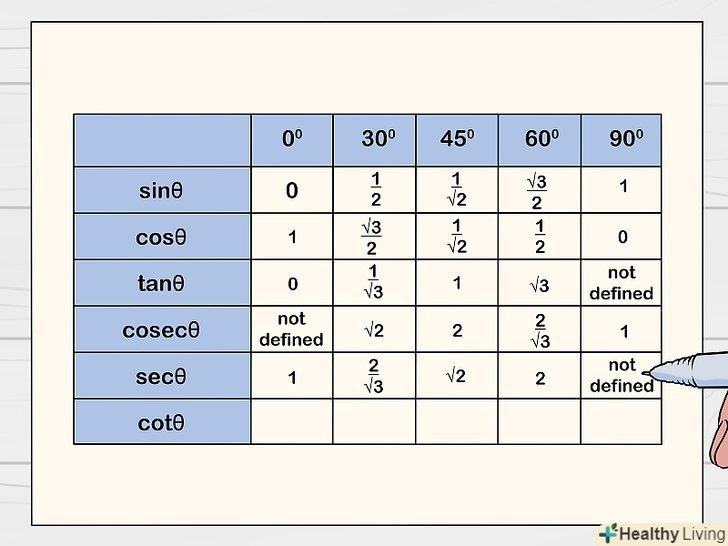
  6. Розділіть 1 на значення рядка "cos«, щоб заповнити рядок»sec".це можна зробити, оскільки sec = 1/cos. Наприклад, cos 60° = 1/2, тому sec 60° = 1/(1/2) = 2.[6]
    • Отже, комірки рядка " sec " заповняться наступним чином:1; 2/√3; √2; 2; -.
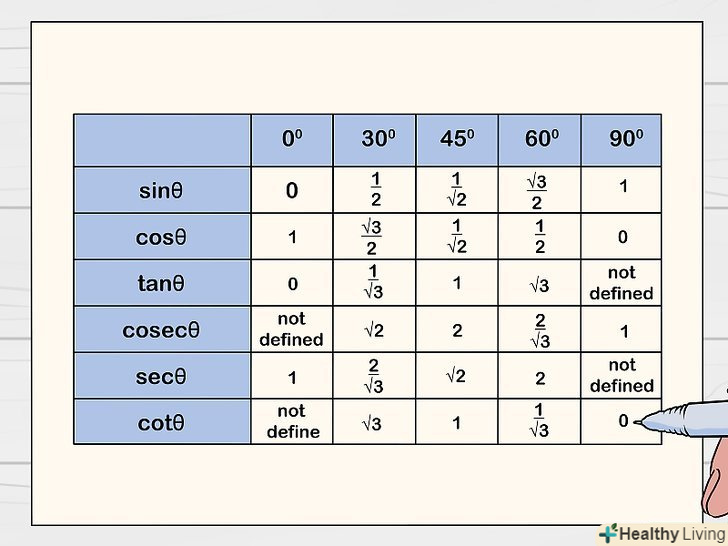
  7. Запишіть значення, які знаходяться в терміні "tg«, в рядку» ctg", але в зворотному порядку.тобто значення tg 90° запишіть в осередку CTG 0°, Значення tg 60° в осередку ctg 30° і так далі. Комірки рядка " ctg " заповняться наступним чином: -; √3; 1; 1/√3; 0.[7]
    • Це можна зробити, оскільки ctg = 1 / tg.
    • Також це вірно, тому що ctg = cos / sin.

Метод2 З 2:
Прямокутний трикутник

  1. Намалюйте прямокутний трикутник з даним (в задачі) кутом.почніть з побудови кута, а саме точки і променів, що виходять з цієї точки під даним кутом. Потім з'єднайте промені відрізком, який буде перпендикулярний одному з променів. Так ви отримаєте прямокутний трикутник, один з кутів якого буде дорівнює даному кутку.[8]
    • Якщо в задачі потрібно обчислити синус, косинус або тангенс кута, швидше за все, сторони прямокутного трикутника будуть дані.
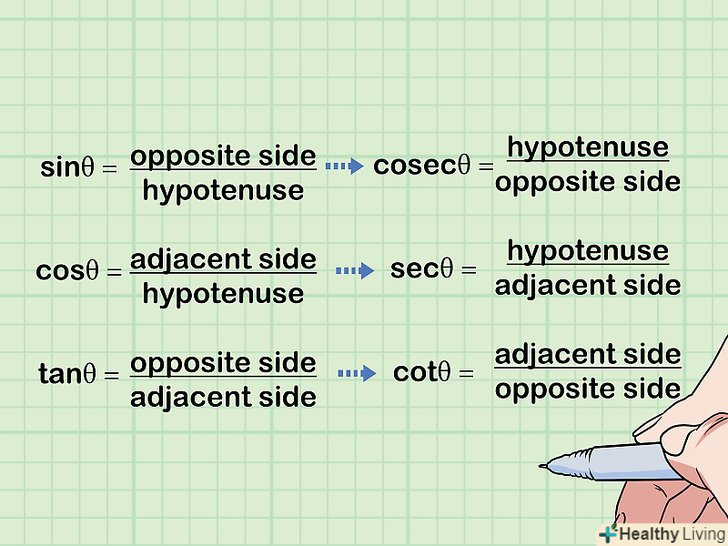
  2. Обчисліть синус, косинус або тангенс по сторонах трикутника.сторони трикутника позначаються наступним чином: протилежний катет (сторона навпроти кута), прилеглий катет (сторона біля кута), гіпотенуза (сторона навпроти прямого кута). Синус, косинус і тангенс можуть бути виражені як різні відносини цих сторін.[9]
    • Синус кута дорівнює відношенню протилежного катета до гіпотенузи.
    • Косинус кута дорівнює відношенню прилеглого катета до гіпотенузи.
    • Тангенс кута дорівнює відношенню протилежного катета до прилеглого.
    • Наприклад, щоб обчислити sin 35°, розділіть довжину протилежного катета на гіпотенузу. Якщо протилежний катет дорівнює 2,8, а гіпотенуза дорівнює 4,9, sin 35° = 2,8/4,9 = 0,57.
  3. Запам'ятайте, які сторони ділити, щоб обчислювати значення тригонометричних функцій. це можна зробити, наприклад, так:» синус навпроти гіпотенуза, косинус біля гіпотенуза, тангенс навпроти біля«, де» навпаки « — це протилежний катет,» біля " — прилеглий катет.[10]
    • Ще раз запам'ятайте: sin = (протилежний катет) / гіпотенуза; cos = (прилеглий катет)/гіпотенуза; tg = (протилежний катет)/(прилеглий катет).
  4. Переверніть відносини, щоб обчислити значення косеканса, секанса і котангенса. якщо ви запам'ятали, які сторони ділити, щоб знайти синус, косинус і тангенс, переверніть відносини сторін, щоб дізнатися, як обчислити косеканс, секанс і котангенс.[11]
    • Cosec = 1 / sin, тому косеканс дорівнює відношенню гіпотенузи до протилежного катету.
    • Sec = 1 / cos, тому секанс дорівнює відношенню гіпотенузи до прилеглого катету.
    • Ctg = 1 / tg, тому котангенс дорівнює відношенню прилеглого катета до протилежного.
    • Наприклад, щоб обчислити cosec 35°, якщо протилежний катет дорівнює 2,8, а гіпотенуза дорівнює 4,9, розділіть 4,9 на 2,8 і отримаєте cosec 35° = 1,75.

Поради

  • Намагайтеся позбавлятися від коренів в знаменниках дробів. Наприклад, tg 30° = 1 / √3. У цьому випадку помножте дріб на √3/√3 (тобто на 1, щоб не змінювати значення вихідної дробу): (1 x √3)/(√3 x √3) = √3/3.

Попередження

  • Ділити на 0 не можна, тому TG 90° або ctg 0° обчислити не вдасться. У таких випадках в осередках таблиці записується символ» -".

Джерела

  1. ↑ Http://www.howtoans.com/2015/03/how-to-remember-trigonometry.html#.W6voJfZRdPY
  2. ↑ Http://www.howtoans.com/2015/03/how-to-remember-trigonometry.html#.W6voJfZRdPY
  3. ↑ Http://www.mathwords.com/t/trig_identities.htm
  4. ↑ Http://www.mathwords.com/t/trig_identities.htm
  5. ↑ Http://www.mathwords.com/t/trig_identities.htm
  6. ↑ Http://www.mathwords.com/t/trig_identities.htm
  7. ↑ Http://www.mathwords.com/t/trig_identities.htm
  8. ↑ Https://www.intmath.com/trigonometric-functions/2-sin-cos-tan-csc-sec-cot.php
  9. ↑ Https://www.intmath.com/trigonometric-functions/2-sin-cos-tan-csc-sec-cot.php
  1. ↑ Https://www.pleacher.com/mp/mfacts/sohcahto.html
  2. ↑ Https://www.intmath.com/trigonometric-functions/2-sin-cos-tan-csc-sec-cot.php

Ще почитати: