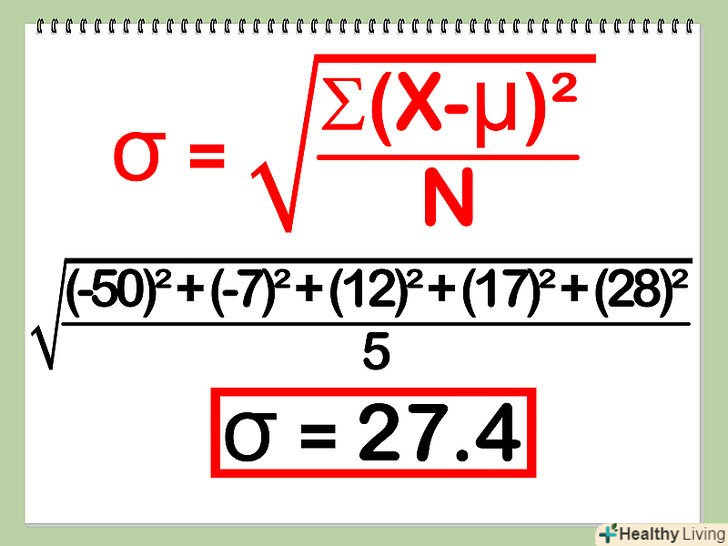Після збору даних їх потрібно проаналізувати. Зазвичай потрібно знайти середнє значення, квадратичне відхилення і похибка. Ми розповімо вам, як це зробити.
Кроки
Метод1З 4:
Дані
Метод1З 4:
 Запишіть числові значення, які ви збираєтеся аналізувати. ми проаналізуємо випадково підібрані числові значення як приклад.
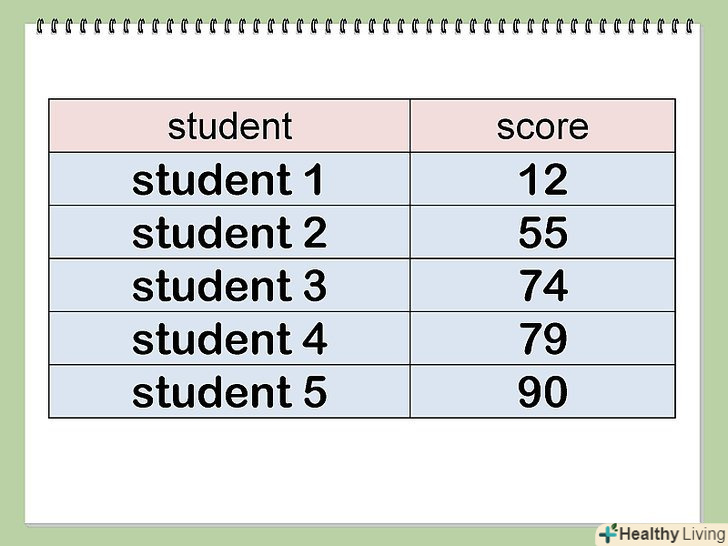
Запишіть числові значення, які ви збираєтеся аналізувати. ми проаналізуємо випадково підібрані числові значення як приклад.- Наприклад, 5 школярам був запропонований письмовий тест. Їх результати (в балах по 100 бальній системі): 12, 55, 74, 79 і 90 балів.
- Наприклад, 5 школярам був запропонований письмовий тест. Їх результати (в балах по 100 бальній системі): 12, 55, 74, 79 і 90 балів.
Метод2З 4:
Середнє значення
Метод2З 4:
 Для того щоб порахувати середнє значення, потрібно скласти всі наявні числові значення і розділити вийшло число на їх кількість.
Для того щоб порахувати середнє значення, потрібно скласти всі наявні числові значення і розділити вийшло число на їх кількість.- Середнє значення (μ) = Σ / N, де Σ сума всіх числових значень, а N кількість значень.
- Тобто, в нашому випадку μ дорівнює (12+55+74+79+90)/5 = 62.
- Середнє значення (μ) = Σ / N, де Σ сума всіх числових значень, а N кількість значень.
Метод3З 4:
Середнє квадратичне відхилення
Метод3З 4:
 Ми будемо вважати середнє відхилення. середнє відхилення = σ = квадратний корінь з [(Σ ((X-μ)^2))/(N)].
Ми будемо вважати середнє відхилення. середнє відхилення = σ = квадратний корінь з [(Σ ((X-μ)^2))/(N)].- Для вищевказаного прикладу це квадратний корінь з [((12-62)^2 + (55-62)^2 + (74-62)^2 + (79-62)^2 + (90-62)^2)/(5)] = 27,4. (Зверніть увагу, що якщо це вибіркове середньоквадратичне відхилення, то ділити потрібно на N-1, де n кількість значень.)
- Для вищевказаного прикладу це квадратний корінь з [((12-62)^2 + (55-62)^2 + (74-62)^2 + (79-62)^2 + (90-62)^2)/(5)] = 27,4. (Зверніть увагу, що якщо це вибіркове середньоквадратичне відхилення, то ділити потрібно на N-1, де n кількість значень.)
Метод4З 4:
Середня похибка середнього значення
Метод4З 4:
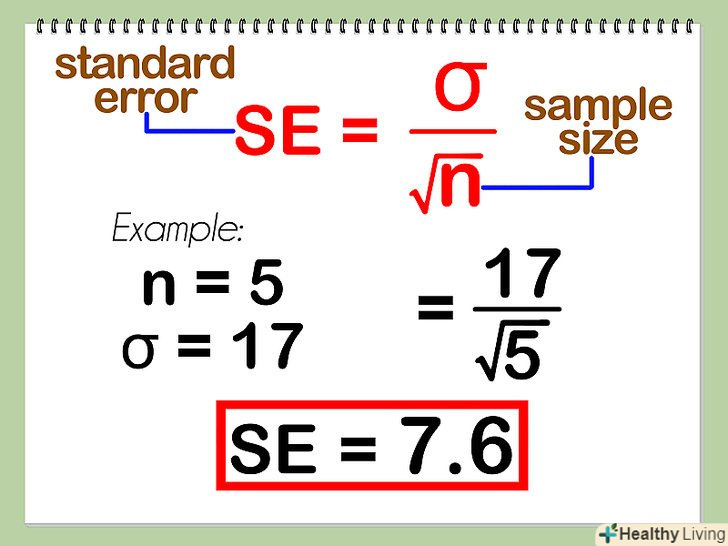
 Вважаємо середню похибку (середнього значення). це оцінка того, наскільки сильно округлюється загальне середнє значення. Чим більше числових значень, тим менше середня похибка, тим точніше середнє значення. Для розрахунку похибки треба розділити середнє відхилення на корінь квадратний від N. стандартна похибка = σ / кв. корінь (n).
Вважаємо середню похибку (середнього значення). це оцінка того, наскільки сильно округлюється загальне середнє значення. Чим більше числових значень, тим менше середня похибка, тим точніше середнє значення. Для розрахунку похибки треба розділити середнє відхилення на корінь квадратний від N. стандартна похибка = σ / кв. корінь (n).- Якщо в нашому прикладі 5 школярів, а всього в класі 50 школярів, і середнє відхилення, пораховане для 50 школярів одно 17 (σ = 21), середня похибка = 17/кв.корінь(5) = 7.6.
- Якщо в нашому прикладі 5 школярів, а всього в класі 50 школярів, і середнє відхилення, пораховане для 50 школярів одно 17 (σ = 21), середня похибка = 17/кв.корінь(5) = 7.6.
Поради
- Розрахунки середнього значення, середнього відхилення і похибки годяться для аналізу рівномірно розподілених даних. Середнє відхилення математичного середнього значення розподілу відноситься приблизно до 68% даних, 2 середніх відхилення – до 95% даних, а 3 – до 99.7% даних. Стандартна похибка ж зменшується при збільшенні кількості значень.
- простий у використанні калькулятор для розрахунку середнього відхилення.
Попередження
- Вважайте двічі. Всі роблять помилки.