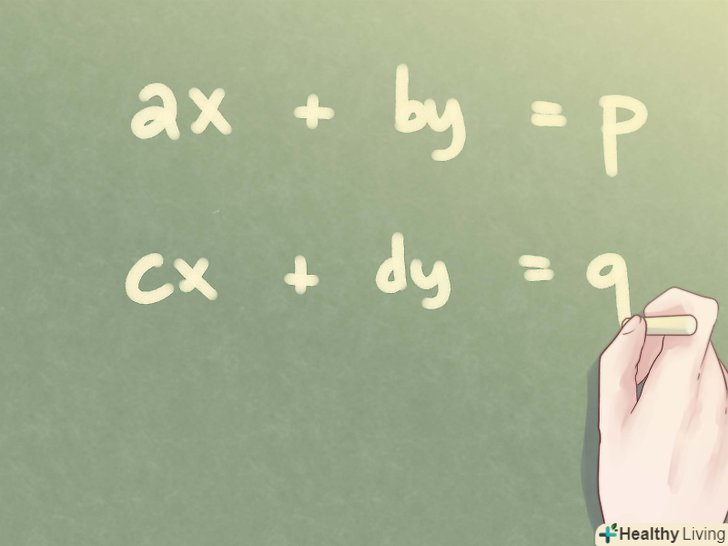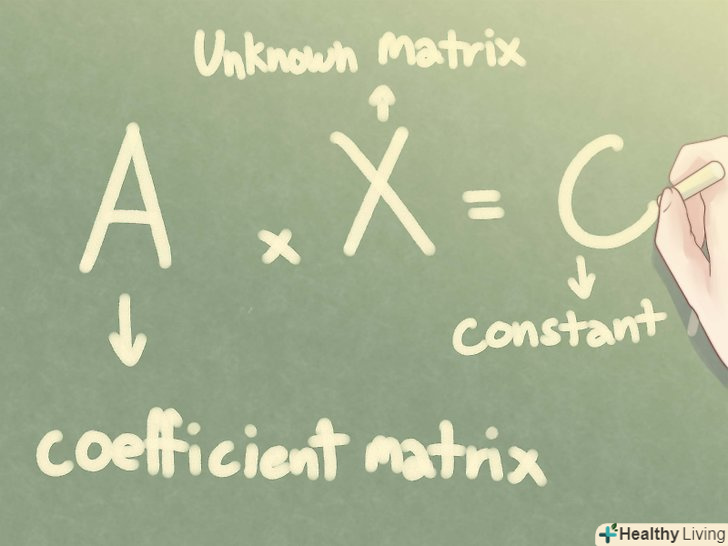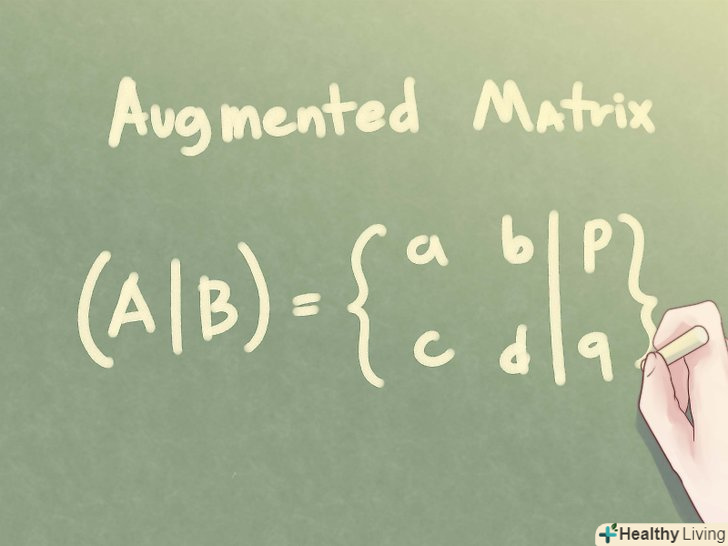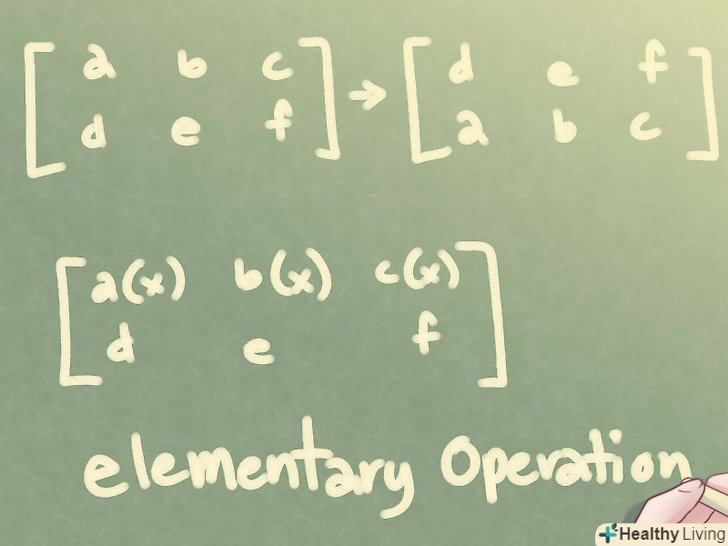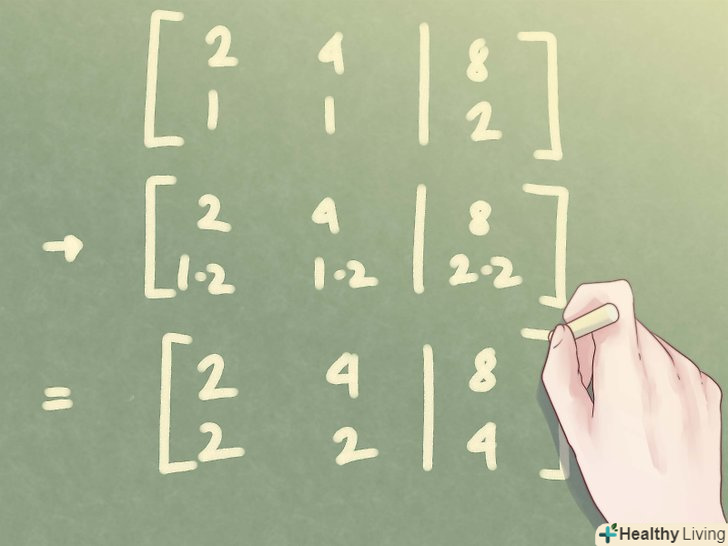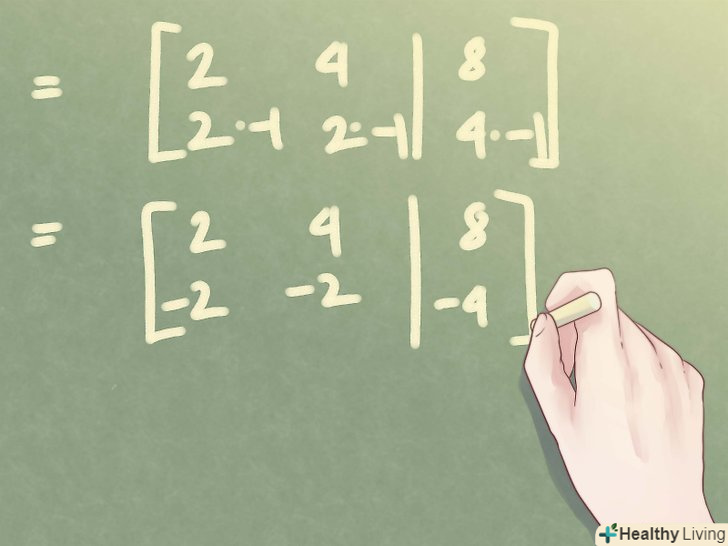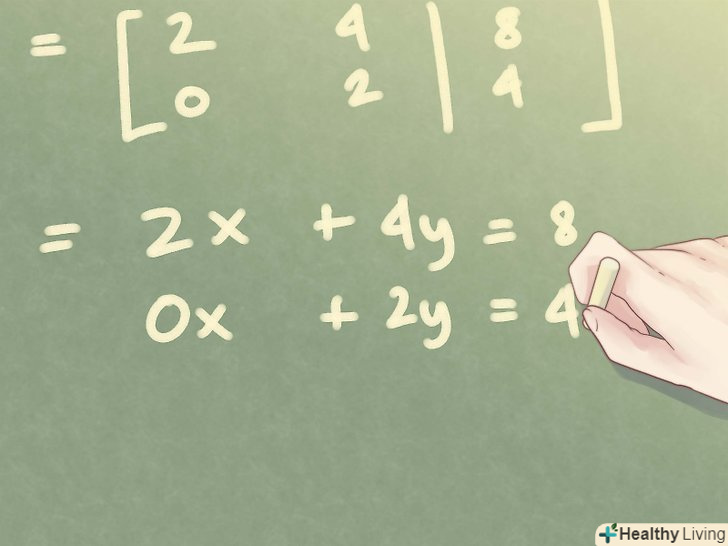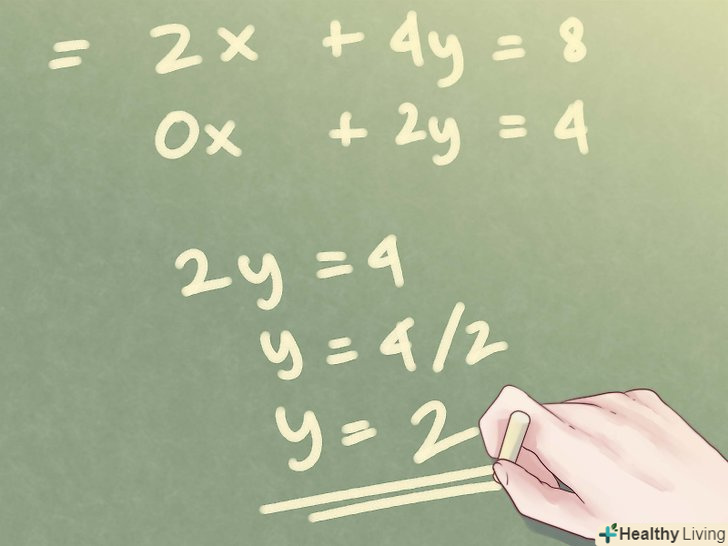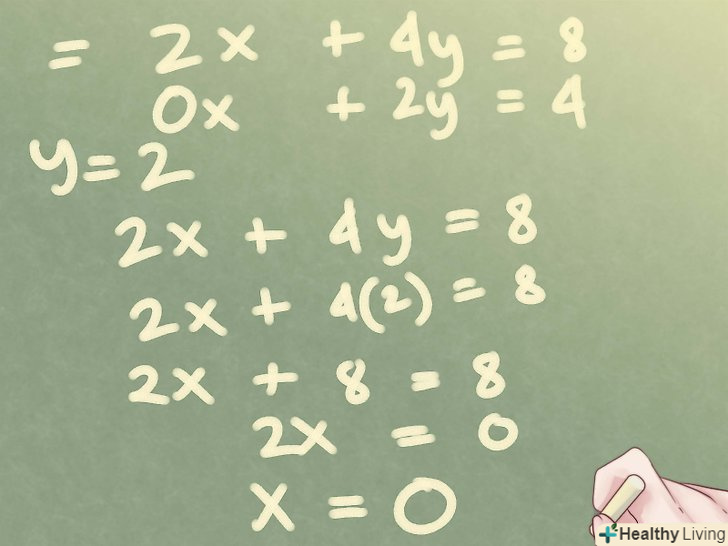Системою рівнянь називається набір з двох або більше рівнянь, які мають загальний набір невідомих і, отже, загальне рішення. Графіком системи лінійних рівнянь є дві прямі, а рішенням системи є точка перетину цих прямих. Для вирішення таких систем лінійних рівнянь корисно і зручно користуватися матрицями.
Кроки
Метод1 З 2:
Частина 1: Основи
Метод1 З 2:
Термінологія.системи лінійних рівнянь складаються з різних компонентів. Змінна позначається буквеним символом (зазвичай x або y) і означає число, яке ви ще не знаєте і яке потрібно знайти. Постійною називається певне число, яке не змінює своє значення. Коефіцієнтом називається число, що стоїть перед змінною, тобто те число, на яке множиться змінна.- Наприклад, для лінійного рівняння 2x + 4y = 8, x і y є змінними, 8 є постійною, а числа 2 і 4 - коефіцієнтами.
-
Форма для системи лінійних рівнянь.Система лінійних алгебраїчних рівнянь (СЛАУ) з двома змінними може бути записана таким чином: ax + by = p, cx + dy = q. будь-які постійні (p, q) можуть бути рівні нулю, але кожне з рівнянь повинно містити хоча б одну змінну (x, y).
-
Матричні вирази.будь-яку СЛАУ можна записати в матричній формі, а потім, використовуючи алгебраїчні властивості матриць, вирішити її. При записі системи рівнянь у формі матриці A являє собою коефіцієнти матриці, C представляє постійні матриці і X позначається невідома матриця.
- Наприклад, представлена вище СЛАУ може бути переписана в наступній матричній формі: A x X = C.
-
Розширена матриця. Розширена матриця виходить шляхом перенесення матриці вільних членів (постійних) в ліву частину. Якщо у вас є дві матриці, A і C, то Розширена матриця буде виглядати наступним чином:
- Наприклад, для наступної системи лінійних рівнянь:
2x + 4y = 8
x + y = 2
Розширена матриця буде мати розмірність 2x3 і виглядати наступним чином:
- Наприклад, для наступної системи лінійних рівнянь:
Метод2 З 2:
Частина 2: Перетворення розширеної матриці для вирішення СЛАУ
Метод2 З 2:
-
Елементарні операції. ви можете робити певні операції над матрицею, отримуючи при цьому матрицю, еквівалентну оригінальній. Такі операції називаються елементарними. Наприклад, щоб вирішити матрицю 2x3 потрібно проводити операції з рядками, щоб привести матрицю до трикутного вигляду. Такими операціями можуть бути:
- Перестановка двох рядків.
- Множення рядка на число, відмінне від нуля.
- Множення рядка і додавання її до іншої.
-
Множення другого рядка на відмінне від нуля число. якщо ви хочете отримати нуль у другому рядку, ви можете помножити рядок так, щоб це стало можливим.
- Наприклад, якщо у вас є матриця такого вигляду:
ви можете зберегти перший рядок і використовувати його для отримання нуля у другому рядку. Для цього необхідно спочатку помножити другий рядок на 2:
- Наприклад, якщо у вас є матриця такого вигляду:
-
Помножте ще раз. щоб отримати нуль для першого рядка, вам може знадобитися помножити ще раз, використовуючи аналогічні маніпуляції.
- У наведеному прикладі необхідно помножити другий рядок на -1:
після множення матриця буде виглядати наступним чином:
- У наведеному прикладі необхідно помножити другий рядок на -1:
- Додайте перший рядок до другої.складіть рядки, щоб отримати нуль на місці елемента першого стовпця і другого рядка.
- У нашому прикладі складіть обидва рядки, щоб вийшло наступне:
-
Запишіть нову систему лінійних рівнянь для трикутної матриці.після того, як ви отримали трикутну матрицю, ви можете знову перейти до СЛАУ. Перший стовпець матриці відповідає невідомій змінній x, а другий відповідає невідомій змінній y. третій стовпець відповідає вільному члену рівняння.
- Для нашого прикладу, нова система лінійних рівнянь набуде вигляду:
-
Вирішіть рівняння для однієї зі змінних.у новій СЛАУ визначте, яку змінну найпростіше знайти і вирішите рівняння.
- У нашому прикладі, зручніше вирішувати з кінця, тобто від останнього рівняння до першого, рухаючись знизу вгору. З другого рівняння ми легко можемо знайти рішення для y, оскільки ми позбулися x, Так, y = 2.
-
Знайдіть другу невідому методом підстановки. після того, як Ви знайшли одну з змінних, ви можете підставити її в друге рівняння, щоб знайти другу змінну.
- У нашому прикладі просто замініть y на 2 у першому рівнянні, щоб знайти невідому x:
Поради
- Елементи матриці зазвичай називають скалярами.
- Щоб вирішити матрицю 2x3, ви повинні виконувати елементарні операції над рядками. Ви не можете виконувати ці операції по стовпцях.
