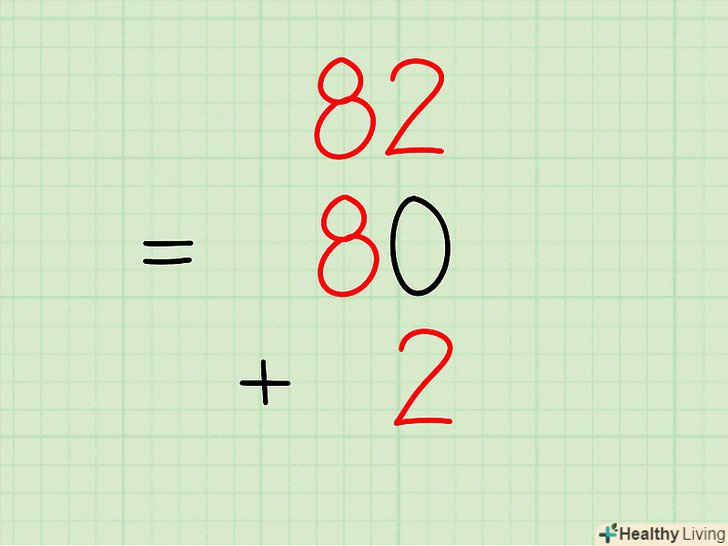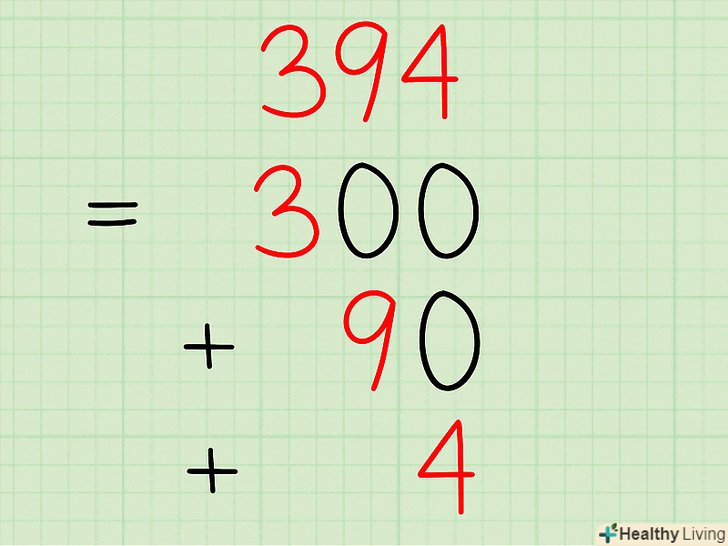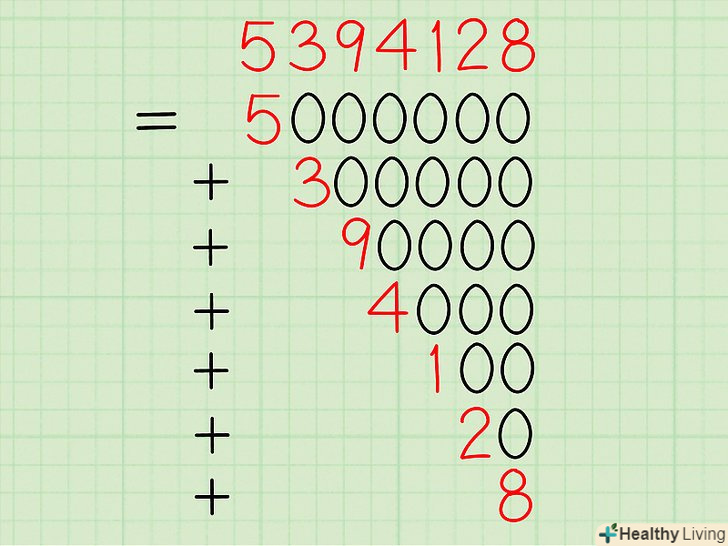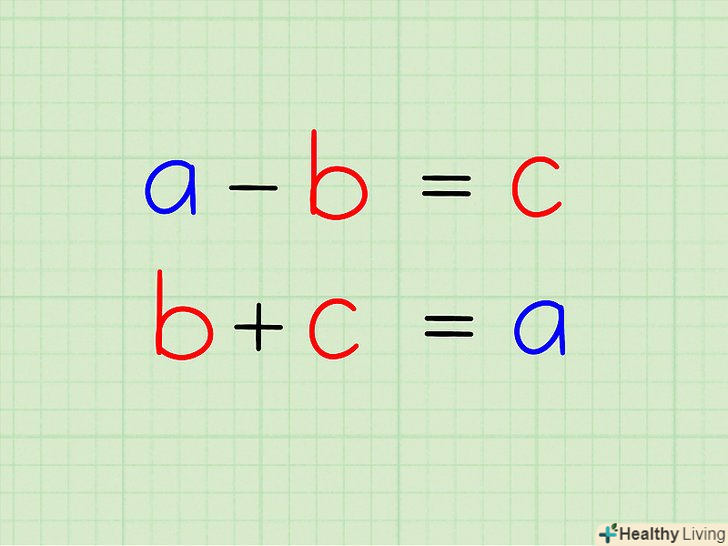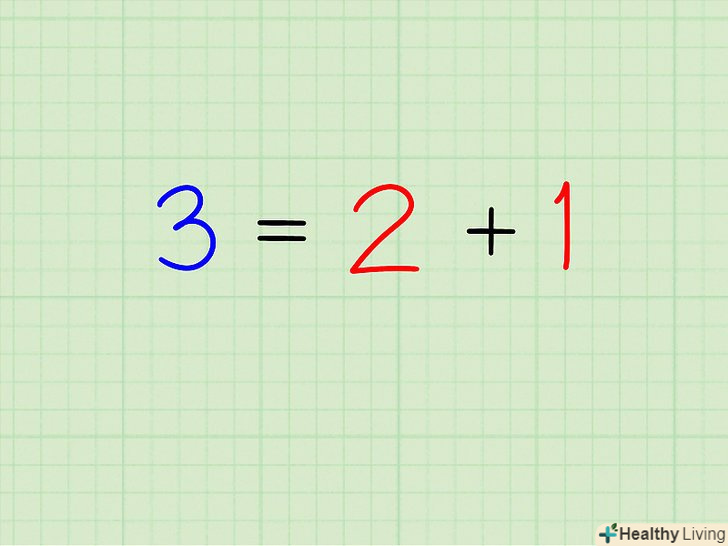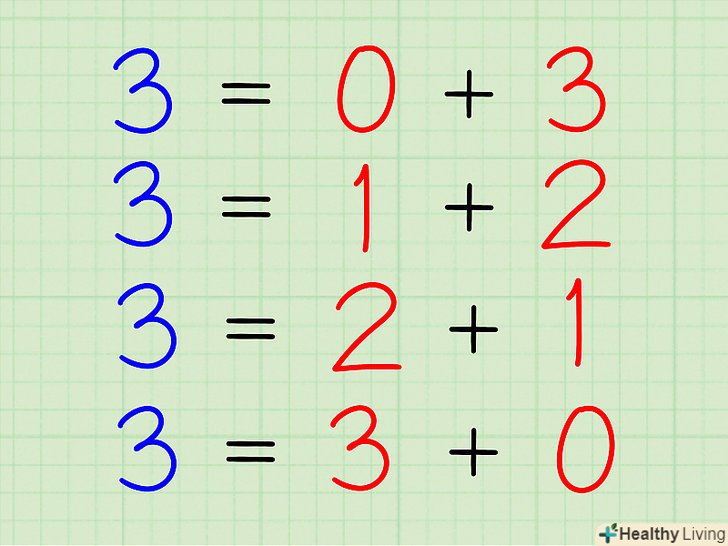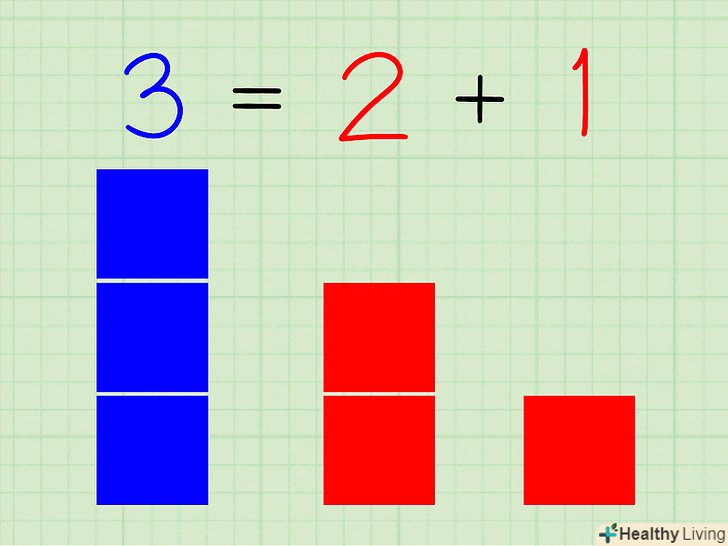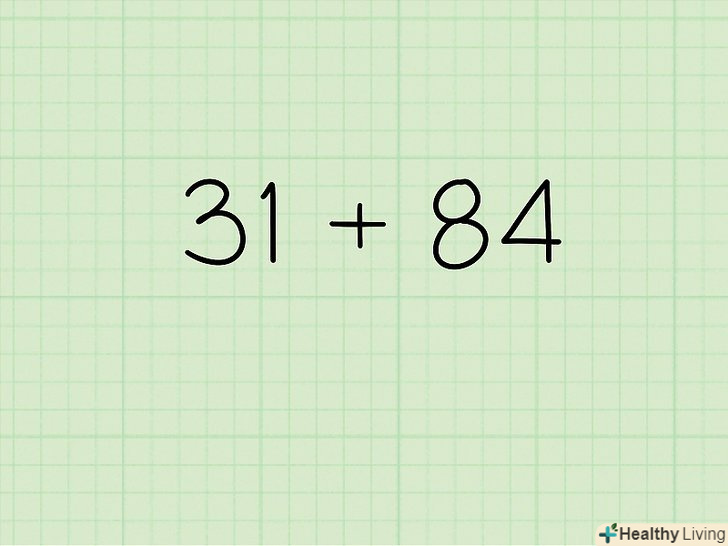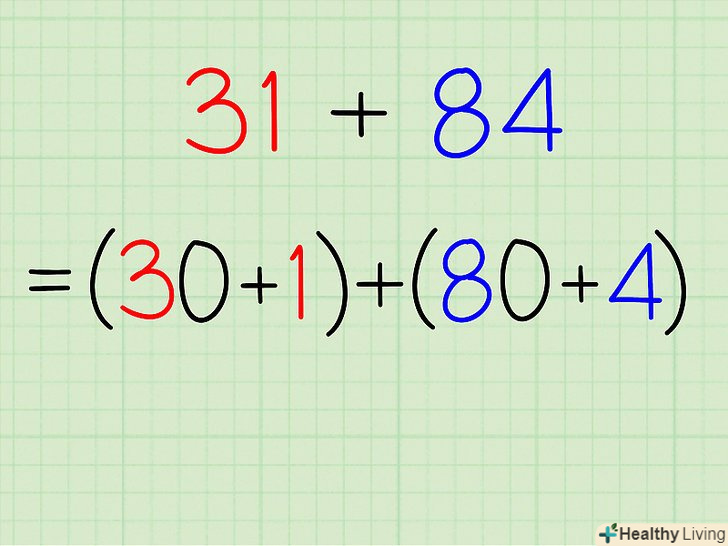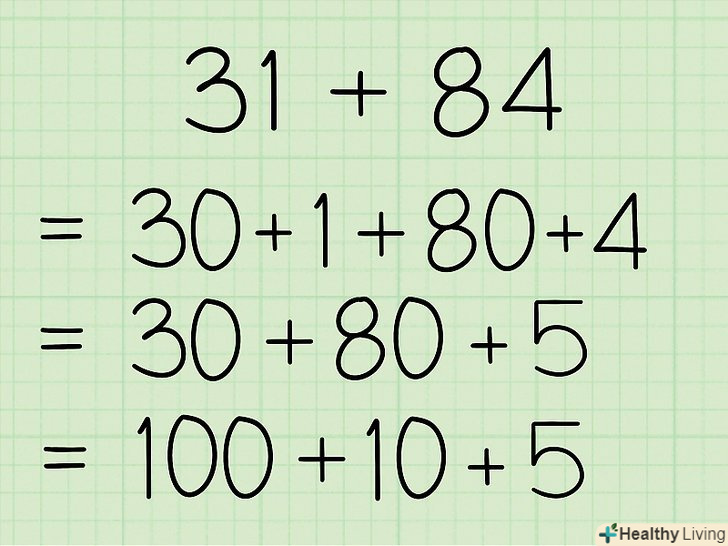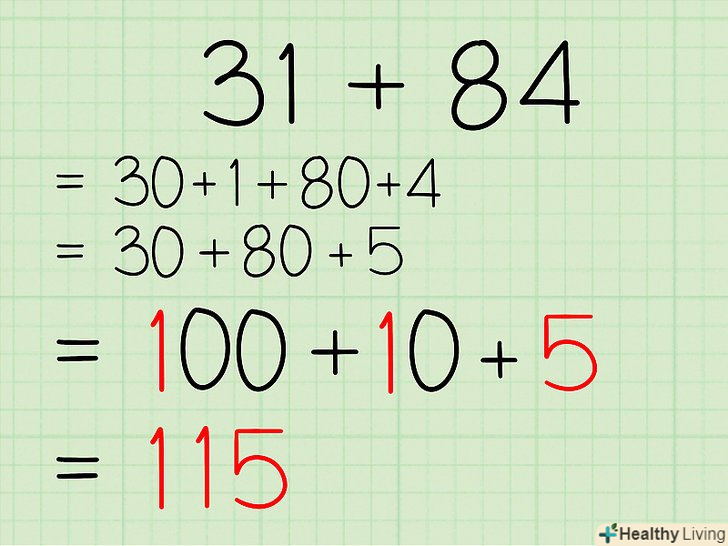1. Головна
    2. Математика
    3. Як розкладати числа-

Як розкладати числа-

Практика розкладання чисел дозволяє студентам зрозуміти закономірності і взаємозв'язку між цифрами в числі і між числами в задачі. Ви можете розкласти число на сотні, десятки і одиниці, або ви можете розкласти число на доданки.

Метод1З 3:
Розкладання на сотні, десятки та одиниці[1]

  1. Зрозумійте різницю між "десятками»і "одиницями". коли ви дивитеся на двозначне число без десяткової коми, позиція цифри зліва називається "десятками«, а цифри» праворуч" – одиницями.
    • Цифра, що стоїть в позиції одиниць, читається так, як є: нуль, один, два, три, чотири, п'ять, шість, сім, вісім, дев'ять.
    • До цифри, що стоїть в позиції десятків, насправді потрібно приписати 0, тобто цифра в позиції десятків означає число, більше числа в позиції одиниць: 10, 20, 30, 40, 50, 60, 70, 80 і 90 (десять, двадцять, тридцять, сорок, п'ятдесят, шістдесят, сімдесят, вісімдесят, дев'яносто).
  2. Розкладіть двозначне число.для цього потрібно знайти кількість десятків і кількість одиниць, а потім написати їх суму.
    • Приклад: розкладіть число 82.
      • Цифра 8 знаходиться в позиції десятків, тому запишіть перший доданок як 80.
      • Цифра 2 знаходиться в позиції одиниць, тому запишіть другий доданок як 2.
      • Напишіть відповідь: 82 = 80 + 2
    • Зверніть увагу, що таке написання числа називається його «розгорнутим видом».
      • У нашому прикладі 80 + 2-це розгорнутий вид числа 82.
  3. У тризначного числа є позиції одиниць, десятків і сотень. позиція сотень знаходиться зліва, позиція десятків посередині, а позиція одиниць справа.
    • Тут позиція одиниць і десятків аналогічна цим позиціям у двозначних числах.
    • До цифри, що стоїть в позиції сотень, насправді потрібно приписати два нуля: 100, 200, 300, 400, 500, 600, 700, 800 і 900 (сто, двісті, триста, чотириста, п'ятсот, шістсот, сімсот вісімсот, дев'ятсот).
  4. Розкладіть тризначне число.для цього потрібно знайти кількість сотень, кількість десятків і кількість одиниць, а потім написати їх суму.
    • Приклад: розкладіть число 394.
      • Цифра 3 знаходиться в позиції сотень, тому запишіть перший доданок як 300.
      • Цифра 9 знаходиться в позиції десятків, тому запишіть другий доданок як 90.
      • Цифра 4 знаходиться в позиції одиниць, тому запишіть третій доданок як 2.
      • Напишіть відповідь: 394 = 300 + 90 + 4
      • У нашому прикладі 300 + 90 + 4 – це розгорнутий вид числа 394.
  5. Застосуйте описаний процес для розкладання нескінченно великих чисел.
    • До цифр в будь-якій позиції потрібно приписати стільки нулів, скільки цифр коштує після даної цифри.
    • Приклад: 5394128 = 5000000 + 300000 + 90000 + 4000 + 100 + 20 + 8
  6. Розкладання десяткових дробів. ви можете розкласти десятковий дріб, але кожна цифра після десяткової коми перетвориться в доданок у вигляді десяткового дробу.
    • Цифра, що йде першою після десяткової коми, знаходиться в позиції десятих.
    • Цифра, що йде другий після десяткової коми, знаходиться в позиції сотих.
    • Цифра, що йде третьою після десяткової коми, знаходиться в позиції тисячних.
  7. Розкладання десяткового дробу необхідно проводити в два етапи: На першому розкладати цілуючи частина дробу, а на другому – дробову частину.
    • Зверніть увагу, що ціла частина дробу (число, що стоїть до десяткової коми) розкладається як ціле число (без десяткової коми).
    • Приклад: розкладіть десятковий дріб 431,58
      • Цифра 4 знаходиться в позиції сотень, тому запишіть перший доданок як 400.
      • Цифра 3 знаходиться в позиції десятків, тому запишіть другий доданок як 30.
      • Цифра 1 знаходиться в позиції одиниць, тому запишіть третій доданок як 1.
      • Цифра 5 знаходиться в позиції десятих, тому запишіть четвертий доданок як 0,5.
      • Цифра 8 знаходиться в позиції сотих, тому запишіть п'ятий доданок як 0,08.
      • Запишіть остаточну відповідь: 431,58 = 400 + 30 + 1 + 0,5 + 0,08

Метод2 З 3:
Розкладання на різні складові[2][3]

  1. У цьому випадку будь-яке число можна розкласти на різні доданки (числа), які при додаванні дають вихідне число.
    • Якщо перший доданок відняти з вихідного числа, ви повинні отримати другий доданок.
    • При додаванні обох доданків ви повинні отримати вихідне число.
  2. Попрактикуйтеся з невеликими числами, наприклад, з однозначним числом.
    • Ви можете застосовувати цей метод поряд з методом, описаним у попередньому розділі, для розкладання великих чисел. Але так як велике число можна розкласти на безліч різних доданків, то застосовувати тільки цей метод для розкладання великих чисел недоцільно.
  3. Знайдіть всі можливі комбінації доданків.для цього першим доданком виберіть найменше число, а потім збільшуйте його і записуйте знайдені комбінації.
    • Приклад: розкладіть число 7 на різні доданки.
      • 7 = 0 + 7
      • 7 = 1 + 6
      • 7 = 2 + 5
      • 7 = 3 + 4
      • 7 = 4 + 3
      • 7 = 5 + 2
      • 7 = 6 + 1
      • 7 = 7 + 0
  4. Якщо хочете, Використовуйте наочні матеріали.це буде корисно тим, хто стикається з цим методом вперше.
    • Наприклад, при розкладанні числа сім візьміть семи горошин.
      • Приберіть одну горошину і порахуйте залишилися горошини. Так ви визначите, що число сім можна розкласти на» один «і»шість".
      • Продовжуйте забирати горошини з початкової купки. Вважайте горошини, які ви забрали, і горошини, що залишилися в купці.
    • Для цього можна використовувати різні предмети: цукерки, аркуші паперу, прищіпки, кнопки.

Метод3 З 3:
Розкладання чисел у задачах[4]

  1. Розгляньте просту задачу на додавання двох чисел. ви можете розкласти числа, щоб спростити завдання і її вирішення.
    • Цей метод годиться для простих завдань на додавання чисел, але стає менш практичним в більш складних задачах.
  2. Розкладіть числа в задачі на десятки і одиниці.більш того, ви можете розкласти десятки і одиниці на доданки, щоб ще більше спростити завдання.
    • Приклад: розкладіть числа і вирішите завдання 31 + 84
      • Ви можете розкласти 31 Так: 30 + 1
      • Ви можете розкласти 84 так: 80 + 4
  3. Перепишіть завдання в простішому вигляді.Скомпонуйте доданки так, щоб скласти числа стало простіше (тобто щоб Ви змогли зробити це в розумі).
    • Приклад: 31 + 84 = 30 + 1 + 80 + 4 = 30 + 80 + 5 = 20 + 80 + 10 + 5 = 100 + 10 + 5
  4. Вирішіть завдання.після того, як ви переписали завдання у вигляді, що спрощує її рішення, просто складіть числа і знайдіть їх суму.
    • Приклад: 100 + 10 + 5 = 115

Джерела

  1. ↑ Http://www.mathsisfun.com/numbers/numbers-compose-decompose.html
  2. ↑ Http://www.simplycenters.com/2012/11/composing-and-decomposing-numbers.html
  3. ↑ Http://www.kindercrazeblog.com/2012/03/getting-interactive-with-common-core.html
  4. ↑ Http://www.kindergartenworks.com/freebie/decomposing-numbers-part-1/

Ще почитати: