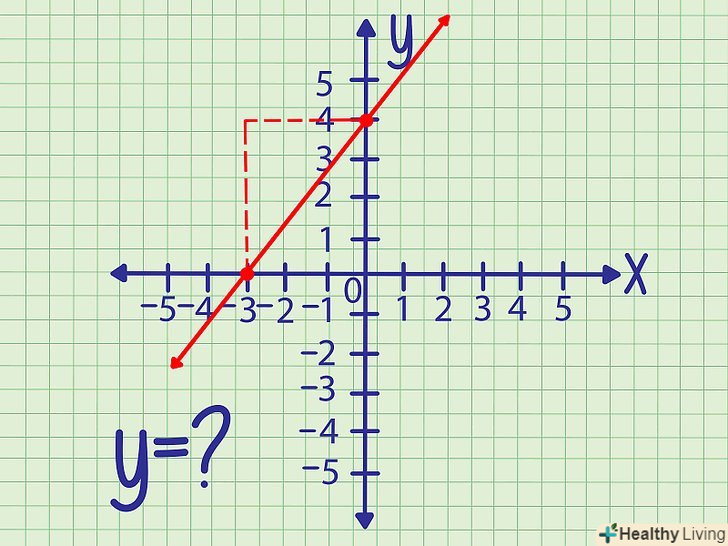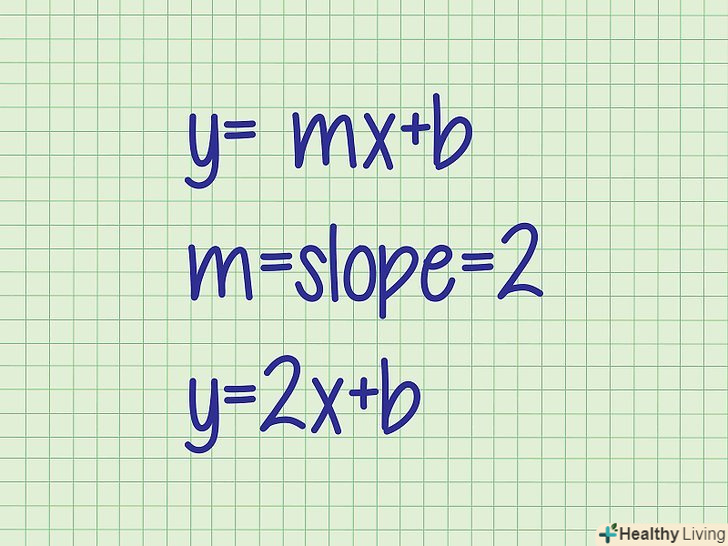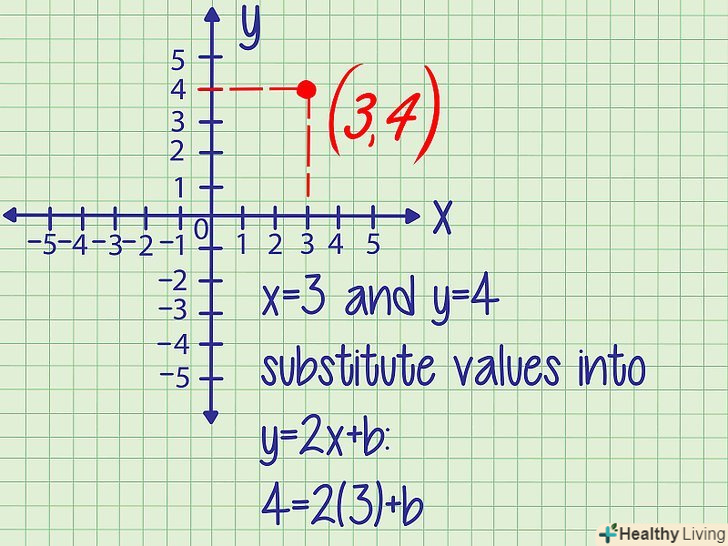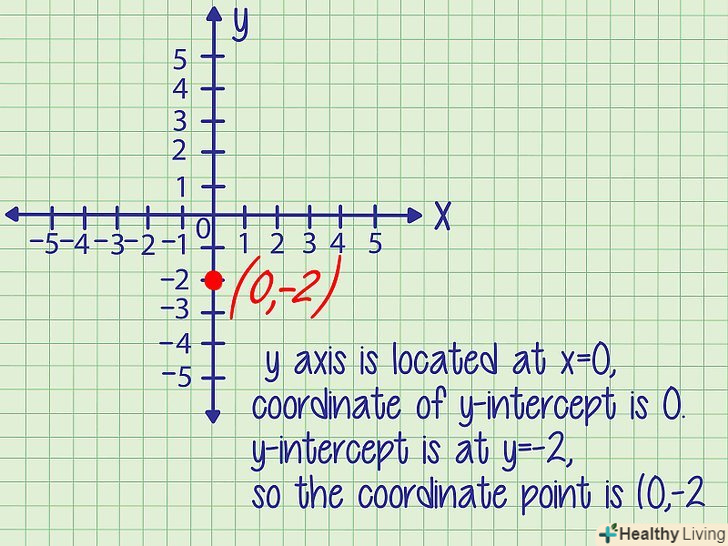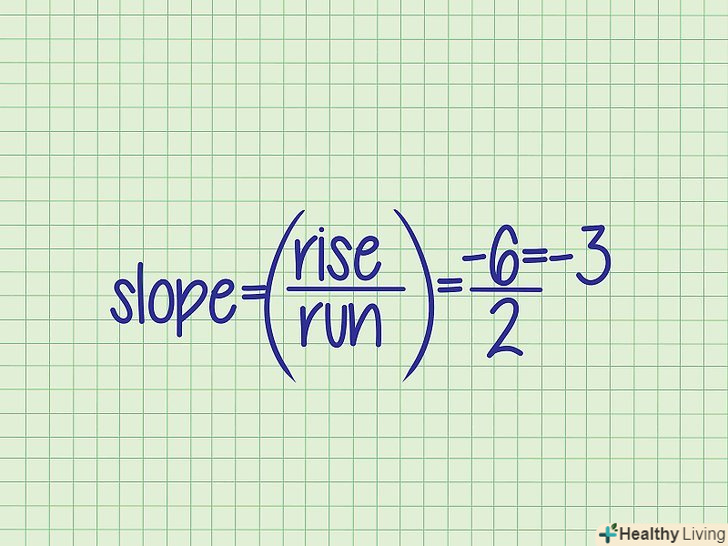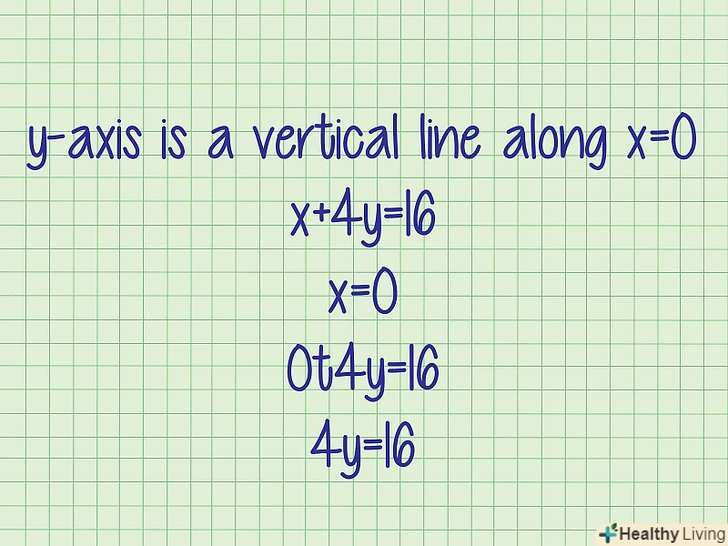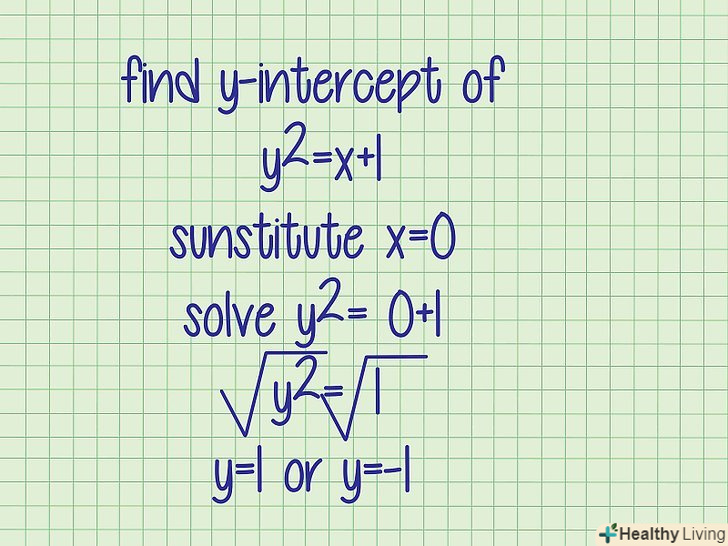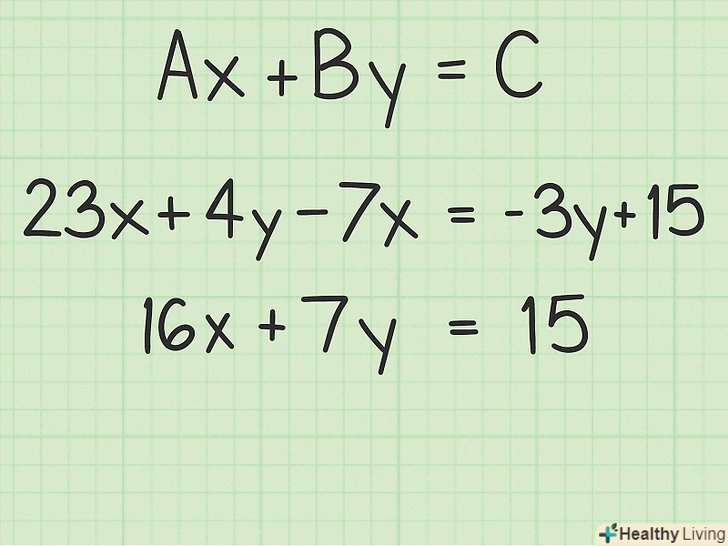Точка перетину з віссю Y-це точка, в якій графік функції перетинає вісь ординат. Знайти таку точку можна декількома способами, в залежності від початкової інформації.
Кроки
Метод1З 3:
По кутовому коефіцієнту і точці
Метод1З 3:
 Запишіть значення кутового коефіцієнта і координати точки. кутовий коефіцієнт характеризує кут нахилу графіка по відношенню до осі X. координати точки, що лежить на графіку, записуються у вигляді (х,у). Якщо вам не дані координати і кутовий коефіцієнт, скористайтеся іншим методом.
Запишіть значення кутового коефіцієнта і координати точки. кутовий коефіцієнт характеризує кут нахилу графіка по відношенню до осі X. координати точки, що лежить на графіку, записуються у вигляді (х,у). Якщо вам не дані координати і кутовий коефіцієнт, скористайтеся іншим методом.- Приклад 1. Дана пряма, на якій лежить точка а (3,4) і кутовий коефіцієнт якої дорівнює 2. Знайдіть точку перетину цієї прямої з віссю Y.
 Запишіть лінійну функцію. Її графік являє собою пряму. Лінійна функція має вигляд у = КХ + b, де k – кутовий коефіцієнт, b – координата «у» точки перетину з віссю Y.
Запишіть лінійну функцію. Її графік являє собою пряму. Лінійна функція має вигляд у = КХ + b, де k – кутовий коефіцієнт, b – координата «у» точки перетину з віссю Y. У функцію підставте значення кутового коефіцієнта.підставте дане значення замістьk.
У функцію підставте значення кутового коефіцієнта.підставте дане значення замістьk.- Приклад 1. y = Kx + b
K = 2
y = 2x + b
- Приклад 1. y = Kx + b
 Замість «х» і» у " підставте дані координати точки.якщо дані координати точки, що лежить на прямій, підставте їх в функцію замість хі у.
Замість «х» і» у " підставте дані координати точки.якщо дані координати точки, що лежить на прямій, підставте їх в функцію замість хі у.- Приклад 1. Точка а (3,4) лежить на прямій. Тобто х = 3, у = 4.
підставте ці значення в Y = 2 X + b
4 = 2 * 3 + b
- Приклад 1. Точка а (3,4) лежить на прямій. Тобто х = 3, у = 4.
 Знайдіть значенняb. нагадаємо, що b - це координата» у " точки перетину з віссю Y. у рівнянні b є єдиною змінною, яку потрібно відокремити і знайти її значення.
Знайдіть значенняb. нагадаємо, що b - це координата» у " точки перетину з віссю Y. у рівнянні b є єдиною змінною, яку потрібно відокремити і знайти її значення.- Приклад 1. 4 = 2*3 + b
4 = 6 + b
4 - 6 = b
-2 = b
Координата «у» точки перетину з віссю Y дорівнює -2 (у = -2).
- Приклад 1. 4 = 2*3 + b
 Відповідь запишіть у вигляді пари координат точки перетину прямої з віссю Y. Точка лежить на перетині прямої і осі Y; координата «х» будь-якої точки, що лежить на осі Y, дорівнює 0, тому координата «х» точки перетину завжди дорівнює 0 (х = 0).
Відповідь запишіть у вигляді пари координат точки перетину прямої з віссю Y. Точка лежить на перетині прямої і осі Y; координата «х» будь-якої точки, що лежить на осі Y, дорівнює 0, тому координата «х» точки перетину завжди дорівнює 0 (х = 0).- Приклад 1. Точка перетину прямої з віссю Y має координати (0,-2).
Метод2 З 3:
За координатами двох точок
Метод2 З 3:
 Запишіть координати двох точок, що лежать на прямій.якщо координати обох точок не дані, скористайтеся іншим методом. Координати кожної точки записуються у вигляді (х,у).
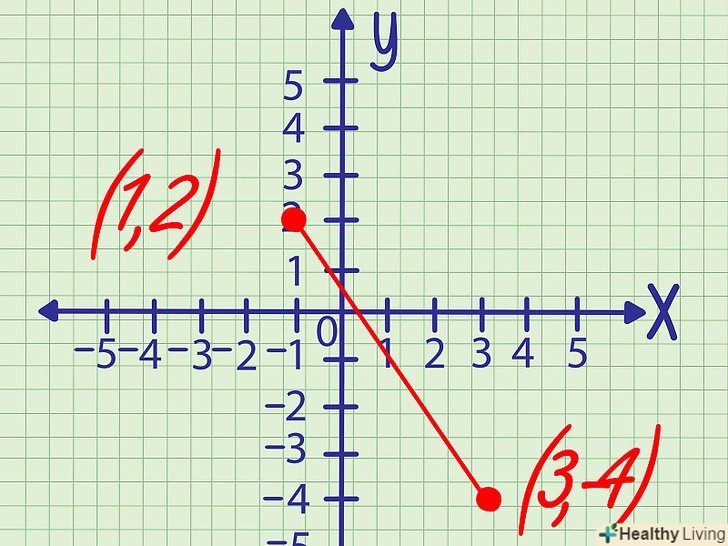
Запишіть координати двох точок, що лежать на прямій.якщо координати обох точок не дані, скористайтеся іншим методом. Координати кожної точки записуються у вигляді (х,у). Приклад 2. пряма проходить через точки А(1,2) і в(3,-4). Знайдіть точку перетину цієї прямої з віссю Y.
Приклад 2. пряма проходить через точки А(1,2) і в(3,-4). Знайдіть точку перетину цієї прямої з віссю Y. Знайдіть вертикальну і горизонтальну відстань між двома точками.кутовий коефіцієнт дорівнює тангенсу кута нахилу прямої, утвореного з віссю Х, і обчислюється як відношення вертикальної відстані між двома точками до горизонтальної відстані між двома точками.
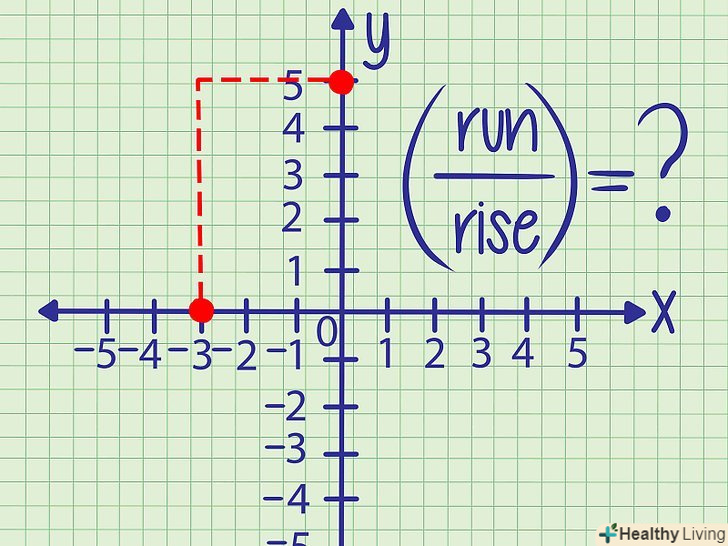
Знайдіть вертикальну і горизонтальну відстань між двома точками.кутовий коефіцієнт дорівнює тангенсу кута нахилу прямої, утвореного з віссю Х, і обчислюється як відношення вертикальної відстані між двома точками до горизонтальної відстані між двома точками.- Вертикальна відстань-це різниця координат» у " двох точок.
- Горизонтальна відстань-це різниця координат» х " двох точок.
- Приклад 2. Координати» у " двох точок: 2 і -4, тому вертикальна відстань: -4 - 2 = -6.
координати» х " двох точок (в тому ж порядку): 1 і 3, тому вертикальне відстань: 3 - 1 = 2.
 Розділіть вертикальну відстань на горизонтальну, щоб знайти кутовий коефіцієнт. знайдені значення підставте в формулу: кутовий коефіцієнт = вертикальна відстань / горизонтальна відстань.
Розділіть вертикальну відстань на горизонтальну, щоб знайти кутовий коефіцієнт. знайдені значення підставте в формулу: кутовий коефіцієнт = вертикальна відстань / горизонтальна відстань.- Приклад 2. k = -6/2 = -3.
 Запишіть лінійну функцію. Її графік являє собою пряму. Лінійна функція має вигляд у = кх + b, де k - кутовий коефіцієнт, b - координата " у " точки перетину з віссю Y. підставте відоме значення кутового коефіцієнта k і координати точки (х,у), щоб знайти b.
Запишіть лінійну функцію. Її графік являє собою пряму. Лінійна функція має вигляд у = кх + b, де k - кутовий коефіцієнт, b - координата " у " точки перетину з віссю Y. підставте відоме значення кутового коефіцієнта k і координати точки (х,у), щоб знайти b. У функцію підставте значення кутового коефіцієнта і координати точки.обчислене значення кутового коефіцієнта підставте замістьk. Координати будь-якої з даних точок підставте замість "х»і "у".
У функцію підставте значення кутового коефіцієнта і координати точки.обчислене значення кутового коефіцієнта підставте замістьk. Координати будь-якої з даних точок підставте замість "х»і "у".- Приклад 2. y= кх + b
k = -3, тому у = - 3x + b
на прямій лежить точка А (1,2), тому 2 = -3 * 1 + b.
- Приклад 2. y= кх + b
 Знайдіть значення b. у рівнянні b є єдиною змінною, яку потрібно відокремити і знайти її значення. Нагадаємо, що координата " х " точки перетину завжди дорівнює 0.
Знайдіть значення b. у рівнянні b є єдиною змінною, яку потрібно відокремити і знайти її значення. Нагадаємо, що координата " х " точки перетину завжди дорівнює 0.- Приклад 2. 2 = -3*1 + b
2 = -3 + b
5 = b
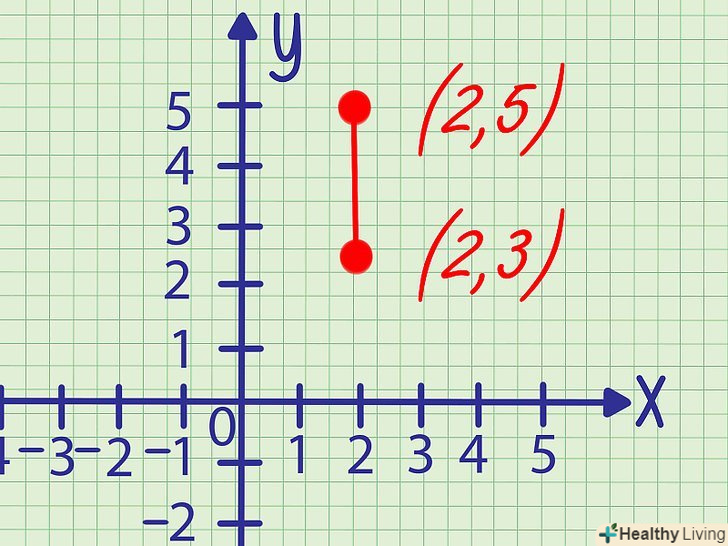
координати точки перетину прямої з віссю Y рівні (0,5).
- Приклад 2. 2 = -3*1 + b
Метод3 З 3:
За допомогою рівняння
Метод3 З 3:
 Запишіть рівняння прямої.якщо дано рівняння, що описує пряму, можна знайти точку її перетину з віссю Y.
Запишіть рівняння прямої.якщо дано рівняння, що описує пряму, можна знайти точку її перетину з віссю Y.- Приклад 3. Знайти точку перетину прямої, яка задана рівнянням х + 4y = 16, з віссю Y.
- Примітка: рівняння, наведене в прикладі 3, описує пряму. В кінці цього розділу наведено приклад квадратного рівняння (в якому змінна зводиться в квадрат).
 Замість» х " підставте 0. нагадаємо, що точка перетину лежить на перетині прямої і осі Y; координата "х «будь-якої точки, що лежить на осі Y, дорівнює 0, тому координата» х" точки перетину завжди дорівнює 0 (х = 0). Підставте х = 0 в рівняння прямої.
Замість» х " підставте 0. нагадаємо, що точка перетину лежить на перетині прямої і осі Y; координата "х «будь-якої точки, що лежить на осі Y, дорівнює 0, тому координата» х" точки перетину завжди дорівнює 0 (х = 0). Підставте х = 0 в рівняння прямої.- Приклад 3. x + 4Y = 16
х = 0
0 + 4y = 16
4y = 16
- Приклад 3. x + 4Y = 16
 Знайдіть "у". Так ви обчислите координату» у " точки перетину з віссю Y.
Знайдіть "у". Так ви обчислите координату» у " точки перетину з віссю Y.- Приклад 3. 4y = 16
у = 4
координати точки перетину прямої з віссю Y рівні (0,4).
- Приклад 3. 4y = 16
 Перевірте відповідь, побудувавши графік (якщо хочете).графік побудуйте якомога більш точно. Точка, в якій пряма перетинає вісь Y, є точкою перетину.
Перевірте відповідь, побудувавши графік (якщо хочете).графік побудуйте якомога більш точно. Точка, в якій пряма перетинає вісь Y, є точкою перетину. Знайдіть точку перетину у випадку квадратного рівняння.змінна (в більшості випадків "х") в квадратному рівнянні зводиться в квадрат. У квадратне рівняння також підставляється х = 0, але майте на увазі, що квадратне рівняння описує параболу, яка може перетинати вісь Y в одній або двох точках або взагалі не перетинати вісь ординат. Це означає, що завдання буде мати 1 або 2 рішення або взагалі не мати рішень.
Знайдіть точку перетину у випадку квадратного рівняння.змінна (в більшості випадків "х") в квадратному рівнянні зводиться в квадрат. У квадратне рівняння також підставляється х = 0, але майте на увазі, що квадратне рівняння описує параболу, яка може перетинати вісь Y в одній або двох точках або взагалі не перетинати вісь ординат. Це означає, що завдання буде мати 1 або 2 рішення або взагалі не мати рішень.- Приклад 4. У рівняння
підставте x = 0 і вирішіть його.
У цьому випадку рівнянняможна вирішити, взявши квадратний корінь з його обох сторін. Пам'ятайте, що при витяганні квадратного кореня потрібно врахувати два значення: негативне і позитивне
y = 1 або y = -1. Таким чином, координати двох точок перетину прямої з віссю Y рівні (0,1) і (0,-1).
- Приклад 4. У рівняння
Поради
- У разі більш складного рівняння постарайтеся відокремити члени зі змінною» у " на одній стороні рівняння.
- У деяких країнах в рівнянні y = kx + b змінні k і b позначаються по-іншому.[1] це не змінює значення лінійної функції.
- Обчислюючи кутовий коефіцієнт, віднімайте координати "х «і координати» у" в будь-якому порядку, але якщо якась точка вважається першою, то і її координати повинні вважатися першими.[2] наприклад, дані координати двох точок: (1,12) і (3, 7). Кутовий коефіцієнт обчислюється двома способами:
- Координати другої точки мінус координати першої точки:
- Координати першої точки мінус координати другої точки:
- Координати другої точки мінус координати першої точки: