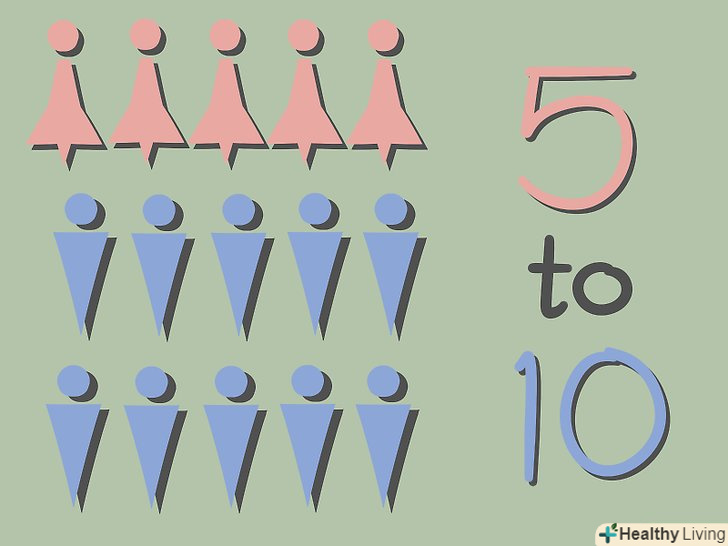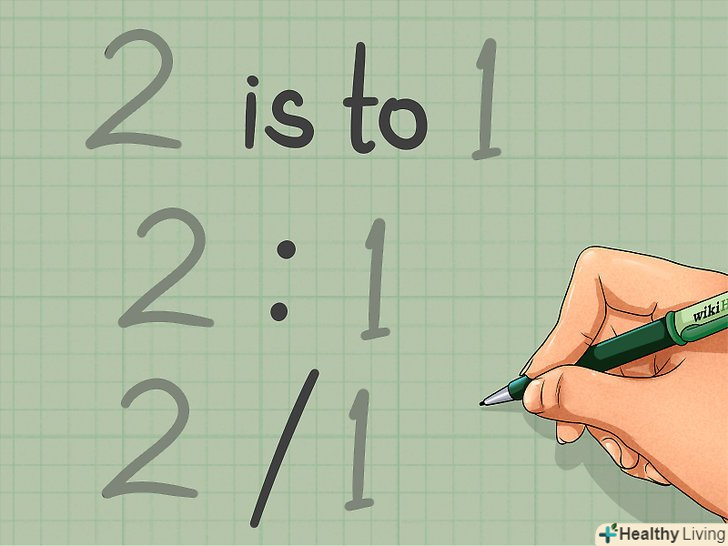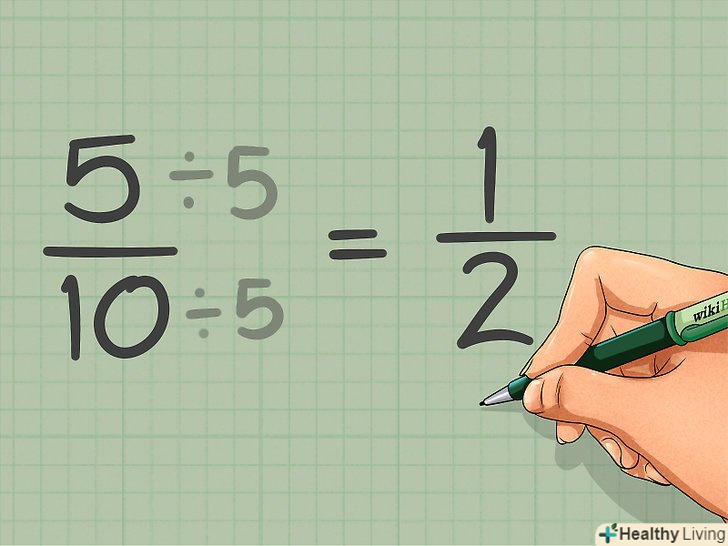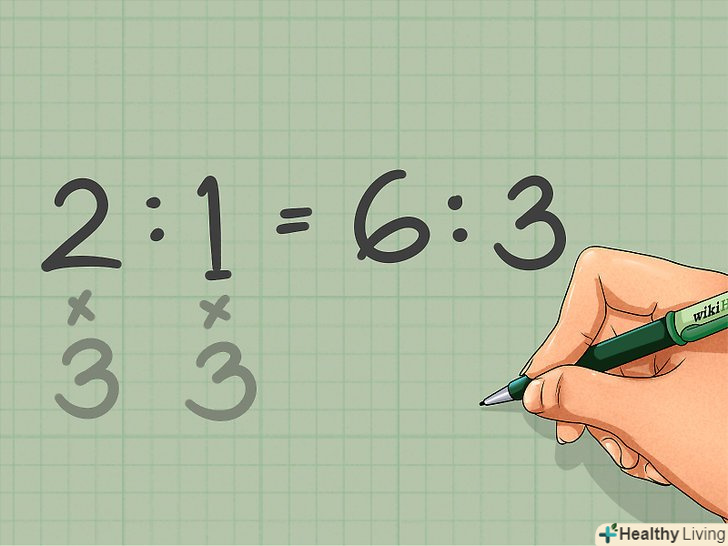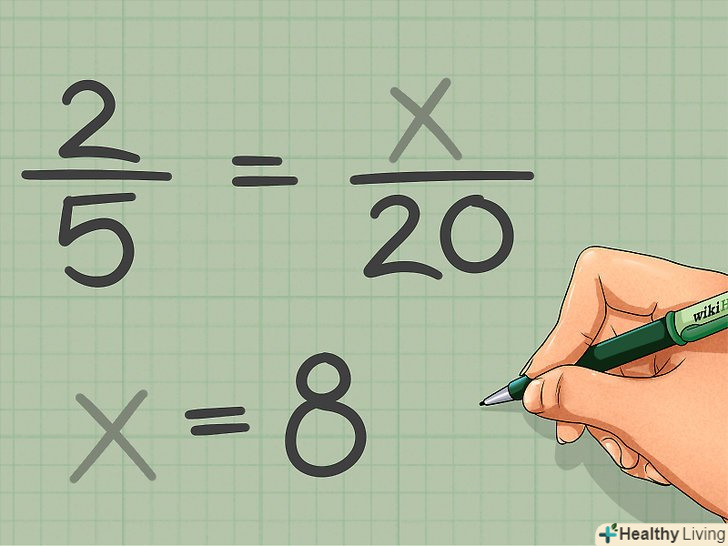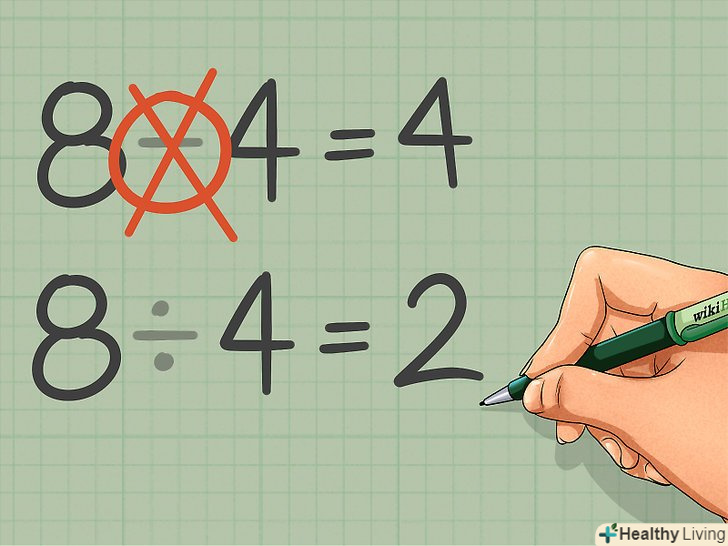1. Головна
    2. Математика
    3. Як обчислювати співвідношення: 9 кроків (з ілюстраціями)

Як обчислювати співвідношення: 9 кроків (з ілюстраціями)

Співвідношення — в математиці) - це взаємозв'язок між двома або більше числами одного роду. Співвідношення порівнюють абсолютні величини або частини цілого. Співвідношення обчислюються і записуються по-різному, але основні принципи однакові для всіх співвідношень.

Частина1З 3:
Визначення співвідношень

  1. Використання співвідношень.співвідношення використовуються як в науці, так і в повсякденному житті для порівняння величин. Найпростіші співвідношення пов'язують тільки два числа, але є співвідношення, що порівнюють три або більше значення. У будь-якій ситуації, в якій присутній більше однієї величини, можна записати співвідношення. Пов'язуючи деякі значення, співвідношення можуть, наприклад, підказати, як збільшити кількість інгредієнтів в рецепті або речовин в хімічній реакції.[1]
  2. Визначення співвідношень. співвідношення-це взаємозв'язок між двома (або більше) значеннями одного роду. Наприклад, якщо для приготування торта необхідні 2 склянки борошна і 1 склянка цукру, то співвідношення борошна до цукру одно 2 до 1.
    • Співвідношення можуть бути використані і в тих випадках, коли дві величини не пов'язані один з одним (як в прикладі з тортом). Наприклад, якщо в класі вчаться 5 дівчаток і 10 хлопчиків, то співвідношення дівчаток до хлопчиків одно 5 до 10. Ці величини (число хлопчиків і число дівчаток) не залежать один від одного, тобто їх значення зміняться, якщо хтось піде з класу або в клас прийде новий учень. Співвідношення просто порівнюють значення величин.
  3. Зверніть увагу на різні способи представлення співвідношень.співвідношення можуть бути представлені словами або за допомогою математичних символів.[2]
    • Дуже часто співвідношення виражені словами (як показано вище). Особливо така форма уявлення співвідношень застосовується в повсякденному житті, далекій від науки.
    • Також співвідношення можна виразити через двокрапку. При порівнянні двох чисел в співвідношенні ви будете використовувати одну двокрапку (наприклад, 7:13); при порівнянні трьох і більше значень ставте двокрапка між кожною парою чисел (наприклад, 10:2:23). У нашому прикладі з класом ви можете висловити співвідношення дівчаток і хлопчиків так: 5 дівчаток: 10 хлопчиків. Або так: 5: 10.
    • Рідше співвідношення виражаються за допомогою похилої риси. У прикладі з класом воно може бути записано так: 5/10. Проте це не дріб і читається таке співвідношення не як дріб; більш того, запам'ятайте, що в співвідношенні цифри не являють собою частину єдиного цілого.

Частина2З 3:
Використання співвідношень

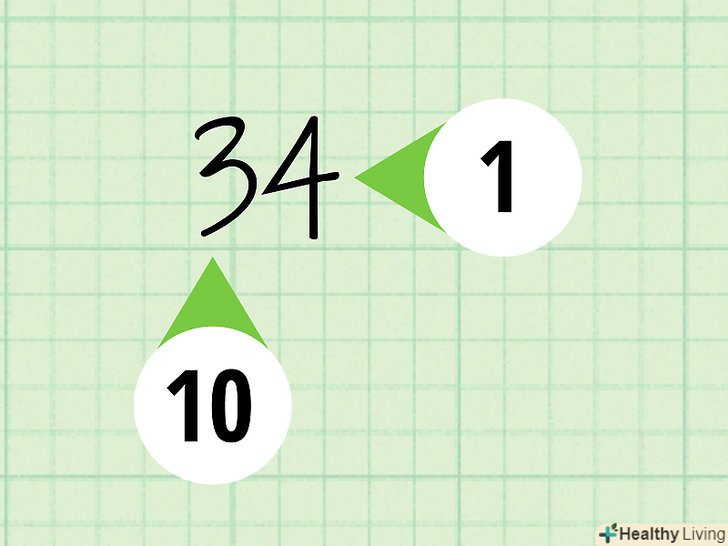
  1. Спростіть співвідношення. співвідношення можна спростити (аналогічно дробів), розділивши кожен член (число) співвідношення на найбільший спільний дільник. Однак при цьому не пропустіть з уваги вихідних значень співвідношення.[3]
    • У нашому прикладі в класі 5 дівчаток і 10 хлопчиків; співвідношення дорівнює 5:10. Найбільший спільний дільник членів співвідношення дорівнює 5 (так як і 5, і 10 діляться на 5). Розділіть кожне число співвідношення на 5 і отримаєте співвідношення 1 дівчинка до 2 хлопчиків (або 1:2). Однак при спрощенні співвідношення пам'ятайте про вихідні значення. У нашому прикладі в класі не 3 учні, а 15. Спрощене співвідношення порівнює кількість хлопчиків і кількість дівчаток. Тобто на кожну дівчинку припадає 2 хлопчика, але в класі не 2 хлопчика і 1 дівчинка.
    • Деякі співвідношення не спрощуються. Наприклад, співвідношення 3:56 не спрощується, так як у цих чисел немає спільних дільників (3 — просте число, а 56 не ділиться на 3).
  2. Використовуйте множення або ділення для збільшення або зменшення співвідношення. поширені завдання, в яких необхідно збільшити або зменшити два значення, пропорційних один одному. Якщо вам дано співвідношення і потрібно знайти відповідне йому більше або менше співвідношення, помножте або розділіть вихідне співвідношення на деяке дане число.[4]
    • Наприклад, пекарю потрібно потроїти кількість інгредієнтів, даних в рецепті. Якщо за рецептом співвідношення борошна до цукру становить 2 до 1 (2:1), то Пекар помножить кожен член співвідношення на 3 і отримає співвідношення 6:3 (6 чашок борошна до 3 чашок цукру).
    • З іншого боку, якщо пекареві необхідно уполовинити кількість інгредієнтів, даних в рецепті, то Пекар розділить кожен член співвідношення на 2 і отримає співвідношення 1:½ (1 чашка борошна до 1/2 чашки цукру).
  3. Пошук невідомого значення, коли дані два еквівалентних співвідношення. це завдання, в якому необхідно знайти невідому змінну в одному співвідношенні за допомогою другого співвідношення, яке еквівалентно першому. Для вирішення таких завдань користуйтеся множенням хрест-навхрест. Запишіть кожне співвідношення у вигляді звичайного дробу, поставте між ними знак рівності і перемножте їх члени хрест-навхрест.[5]
    • Наприклад, дана група учнів, в якій 2 хлопчика і 5 дівчаток. Яке буде число хлопчиків, якщо число дівчаток збільшити до 20 (пропорція зберігається)? По-перше, запишіть два співвідношення - 2 хлопчика:5 дівчаток іХ хлопчиків:20 дівчаток. Тепер запишіть ці співвідношення у вигляді дробів: 2/5 і х/20. Перемножте члени дробів хрест-навхрест і отримаєте 5x = 40; отже, х = 40/5 = 8.

Частина3З 3:
Поширені помилки

  1. Уникайте додавання і віднімання в текстових завданнях на співвідношення.багато текстових завдань виглядають приблизно так: "у рецепті необхідно використовувати 4 бульби картоплі і 5 коренеплодів моркви. Якщо ви хочете додати 8 бульб картоплі, то скільки знадобиться моркви, щоб співвідношення залишилося незмінним?"При вирішенні подібних завдань учні часто припускаються помилки, додаючи однакову кількість інгредієнтів до вихідного числа. Однак, щоб зберегти співвідношення, потрібно використовувати множення. Ось приклади правильного і неправильного рішення:
    • Невірно: «8 - 4 = 4 — так ми додали 4 бульби картоплі. Значить, потрібно взяти 5 коренеплодів моркви і до них додати ще 4... Стоп! Співвідношення так не обчислюють. Варто спробувати знову".
    • Вірно: "8 ÷ 4 = 2 — значить, ми помножили кількість картоплі на 2. Відповідно, 5 коренеплодів моркви теж потрібно помножити на 2. 5 x 2 = 10 — в рецепт потрібно додати 10 коренеплодів моркви».
  2. Перетворіть члени в ті ж одиниці виміру.деякі текстові завдання спеціально ускладнюють, додаючи різні одиниці виміру. Перетворіть їх, перш ніж обчислювати співвідношення. Ось приклад завдання і рішення:
    • У дракона є 500 грам золота і 10 кілограм срібла. Яке співвідношення золота до срібла в Скарбниці дракона?
    • Грами і кілограми — різні одиниці виміру, їх потрібно перетворити. 1 кілограм = 1000 грам, відповідно, 10 кілограм = 10 кілограм x 1000 грам/1 кілограм = 10 x 1000 грам = 10 000 грам.
    • У дракона в Скарбниці 500 грам золота і 10 000 грам срібла.
    • Співвідношення золота до срібла дорівнює: 500 грам золота/10 000 грам срібла = 5/100 = 1/20.
  3. Записуйте одиниці виміру після кожної величини.у текстових завданнях набагато простіше розпізнати помилку, якщо записувати одиниці виміру після кожного значення. Пам'ятайте, що величини з одними і тими ж одиницями виміру в чисельнику і знаменнику скорочуються. Скоротивши вираз, Ви отримаєте правильну відповідь.
    • Приклад: дано 6 коробок, в кожній третій коробці знаходиться 9 кульок. Скільки всього кульок?
    • Невірно: 6 коробок x 3 коробки / 9 кульок = ... Стоп, нічого не можна скоротити. Відповідь буде такою « "коробки x коробки / кульки". Він не має сенсу.
    • Вірно: 6 коробок x 9 кульок / 3 коробки = 6 коробок * 3 кульки/1 коробку = 6 коробок * 3 кульки/1 коробку = 6 * 3 кульки/1 = 18 кульок.

Джерела

  1. ↑ Http://www.virtualnerd.com/common-core/grade-6/6_RP-ratios-proportional-relationships/A
  2. ↑ Http://www.purplemath.com/modules/ratio.htm
  3. ↑ Http://www.helpwithfractions.com/math-homework-helper/least-common-denominator/
  4. ↑ Http://www.mathplanet.com/education/algebra-1/how-to-solve-linear-equations/ratios-and-proportions-and-how-to-solve-them
  5. ↑ Http://www.math.com/school/subject1/lessons/S1U2L2DP.html

Ще почитати: