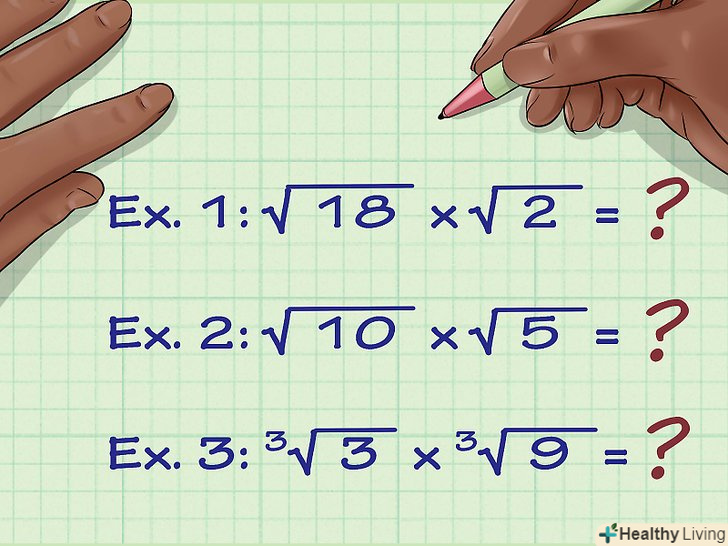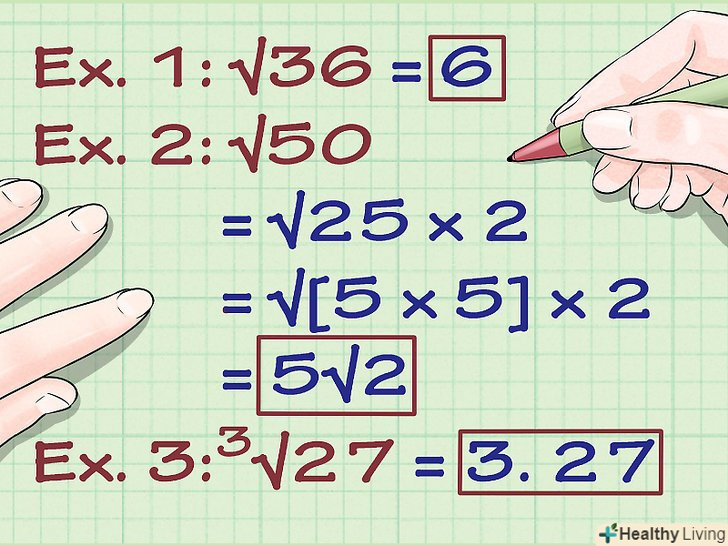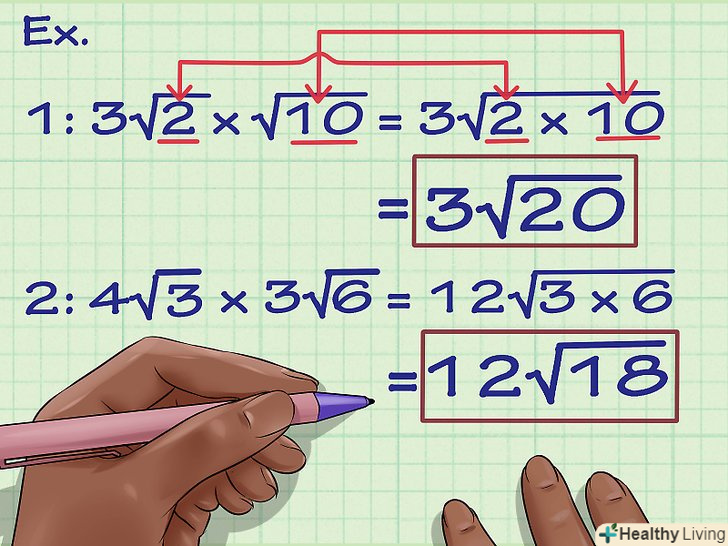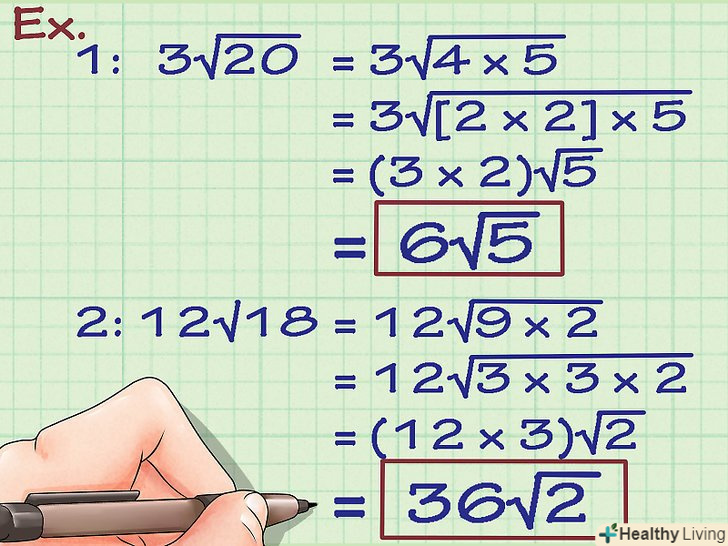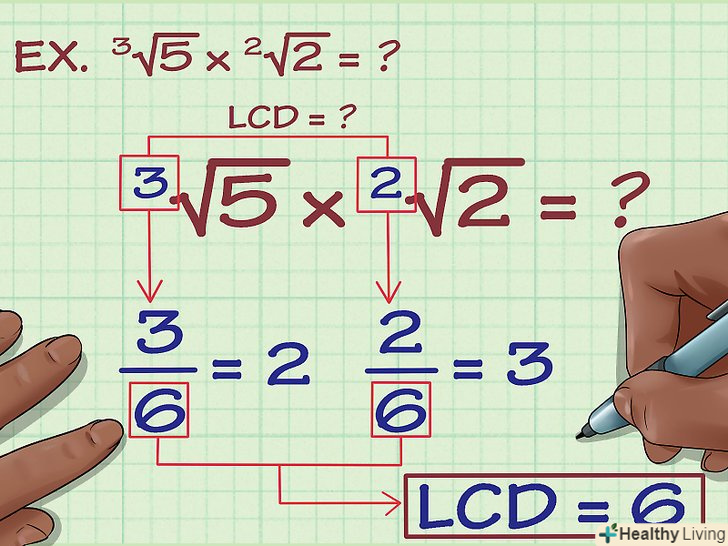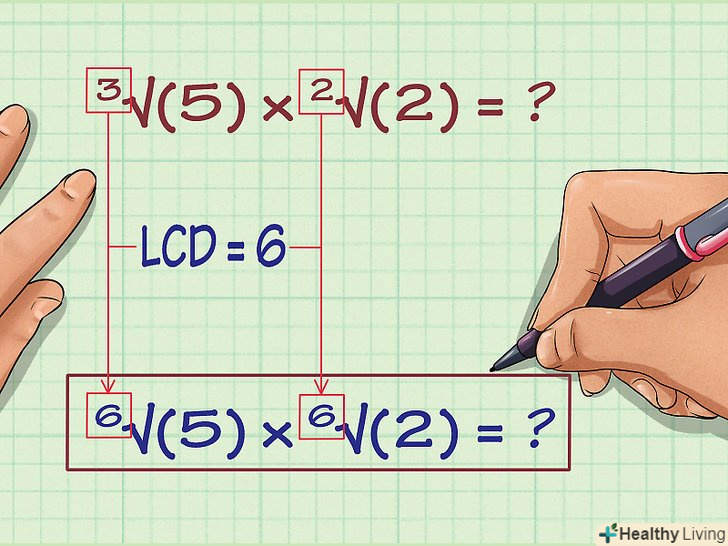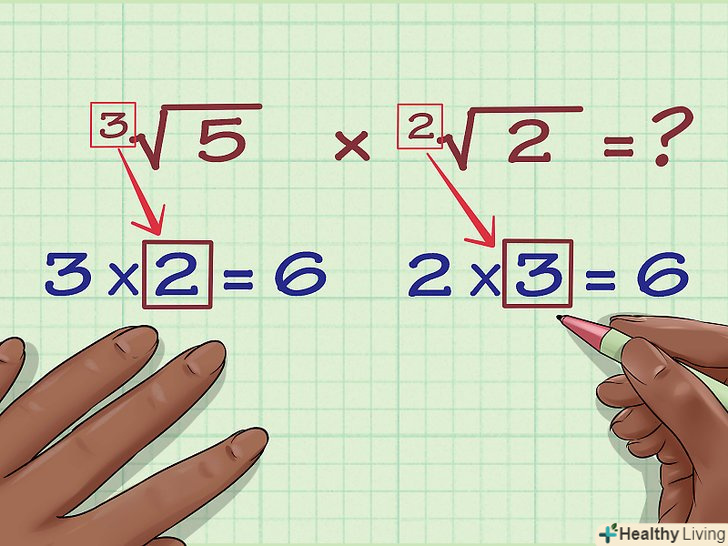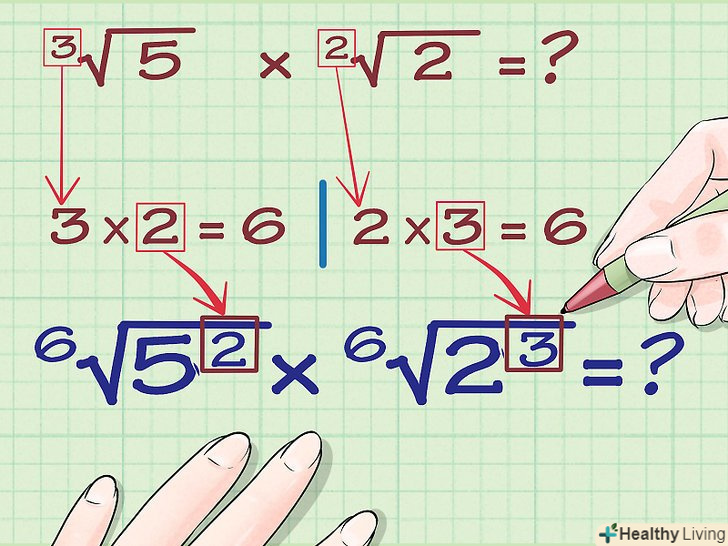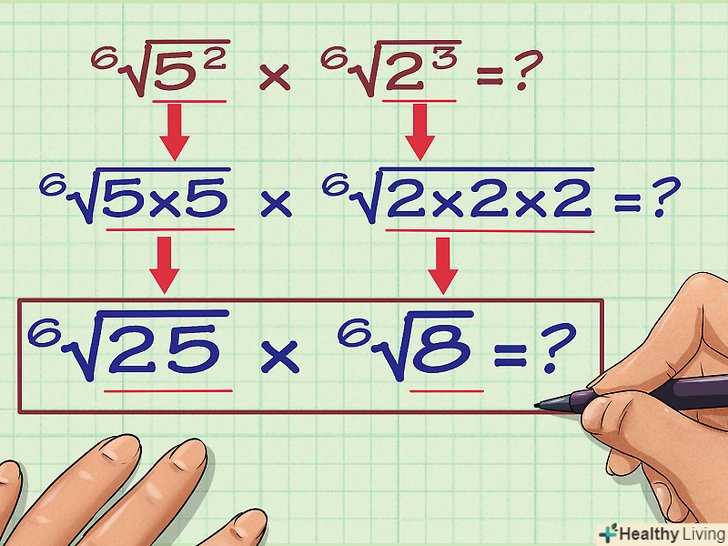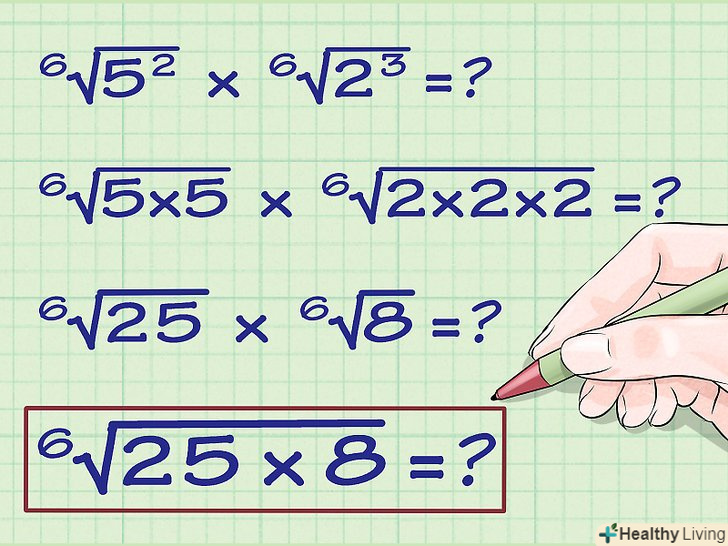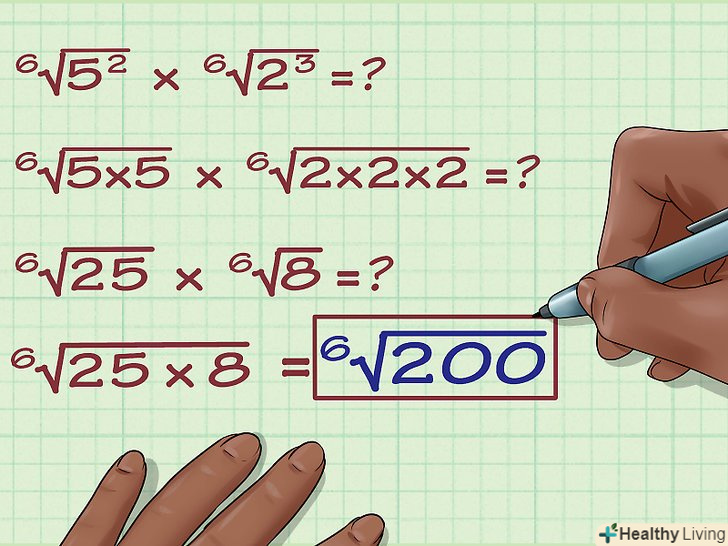1. Головна
    2. Математика
    3. Як множити коріння-

Як множити коріння-

Знак кореня ( √ ) означає Квадратний корінь з деякого числа. Знак кореня зустрічається не тільки в алгебрі, але і в повсякденному житті, наприклад, в деревообробному виробництві, яке включає розрахунок відносних розмірів. Два будь-яких кореня з однаковими показниками (ступеня кореня) можна множити. Якщо біля коріння різні показники, необхідно привести коріння до одного показника. Якщо ви хочете дізнатися, як множити коріння з або без множників, прочитайте цю статтю.

Метод1З 3:
Множення коренів без множників

  1. Переконайтеся, що коріння мають однаковий показник (ступінь).ступінь записується зліва над знаком кореня. Якщо ступеня немає, то корінь вважається квадратним (тобто його ступінь дорівнює 2) і його можна помножити на інші квадратні коріння (про множення коренів з різними показниками читайте далі). Ось кілька прикладів множення коренів з однаковими показниками:
    • Приклад 1: √(18) x √(2) = ?
    • Приклад 2: √(10) x √(5) = ?
    • Приклад 3:3 √(3) x3 √(9) = ?
  2. Перемножте числа під коренем. Ось як це робиться:
    • Приклад 1: √(18) x √(2) = √(36)
    • Приклад 2: √(10) x √(5) = √(50)
    • Приклад 3:3 √(3) x3 √(9) = 3√(27)
  3. Спростіть підкорене вираз. при множенні коренів отримане підкорене вираз можна спростити (не завжди) до добутку деякого числа (або виразу) на повний квадрат або куб. Ось як це робиться:
    • Приклад 1: √(36) = 6. 36 є квадратом числа 6, тому що 6 * 6=36.
    • Приклад 2: √(50) = √(25*2) = √([5*5]*2) = 5√(2). Число 50 можна розкласти на добуток чисел 25 і 2. Корінь з 25 дорівнює 5, тому виносимо 5 за знак кореня і таким чином спрощуємо підкорене вираз.
      • Якщо внести число 5 назад під знак кореня, воно зводиться в квадрат, і ви отримаєте число 25 під знаком кореня.
    • Приклад 3:3 √(27) = 3. Кубічний корінь з числа 27 дорівнює 3, тому що 3*3*3 = 27.

Метод2 З 3:
Множення коренів з множниками

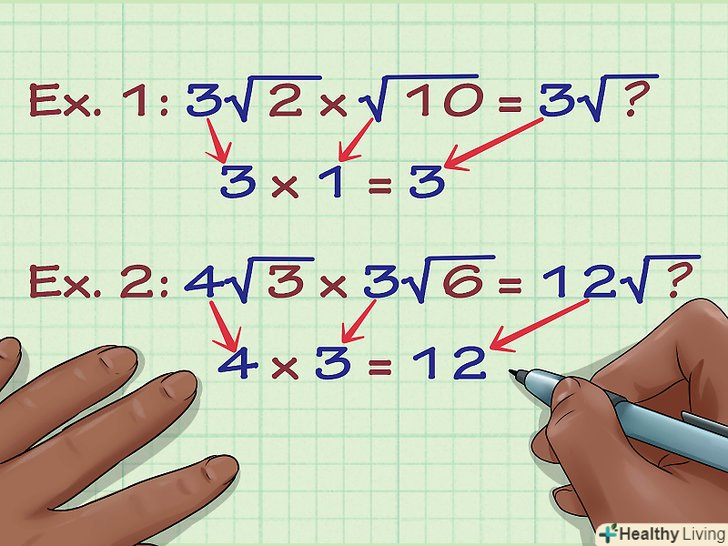
  1. Помножте множники.множник-число, що стоїть перед знаком кореня. Якщо його немає, то множник дорівнює 1. Перемножьте множники. Ось як це робиться:
    • Приклад 1: 3√(2) x √(10) = 3√(?)
      • 3 x 1 = 3
    • Приклад 2: 4√(3) x 3√(6) = 12√(?)
      • 4 x 3 = 12
  2. Помножте числа під знаком кореня.після того як ви перемножили множники, перемножте числа під знаком кореня. Ось як це робиться:
    • Приклад 1: 3√(2) x √(10) = 3√(2 x 10) = 3√(20)
    • Приклад 2: 4√(3) x 3√(6) = 12√(3 x 6) = 12√(18)
  3. Спростіть підкорене вираз.далі спростіть отримані значення під знаком кореня, винісши відповідні числа за знак кореня. Після цього просто перемножте ці винесені числа і множники, що стоять перед знаком кореня. Ось як це робиться:
    • 3√(20) = 3√(4 x 5) = 3√([2 x 2] x 5) = (3 x 2)√(5) = 6√(5)
    • 12√(18) = 12√(9 x 2) = 12√(3 x 3 x 2) = (12 x 3)√(2) = 36√(2)

Метод3 З 3:
Множення коренів з різними показниками

  1. Знайдіть НОК (найменше загальне кратне) показників.НОК показників-найменше число, яке ділиться на обидва показники. Знайдіть НОК показників для наступного виразу:3√(5) x 2√(2) = ?
    • Показники рівні 3 і 2. Число 6 є НОК цих двох чисел, тому що це найменше число, яке ділиться без залишку як на 3, так і на 2: 6/3=2 і 6/2=3. Щоб помножити коріння, їх показник повинен дорівнювати 6.
  2. Запишіть кожен корінь з НОК в якості нового показника. Ось як записати вираз з новим показником:
    • 6√(5) x 6√(2) = ?
  3. Знайдіть числа, на які необхідно помножити кожен вихідний показник, щоб отримати НОК. у виразі 3√(5) Вам потрібно помножити показник 3 на 2, щоб отримати 6. У виразі 2√(2) вам потрібно помножити показник 2 на 3, щоб отримати 6.
  4. Зведіть число, що стоїть під знаком кореня, в ступінь рівну числу, знайденому в попередньому кроці. для першого виразу зведіть 5 в ступінь 2. Для другого виразу зведіть 2 в ступінь 3. Ось як це буде виглядати:
    • 2 --&#gt; 6√(5) = 6√(5)2
    • 3 --&#gt; 6√(2) = 6√(2)3
  5. Виконайте операцію зведення в ступінь і запишіть результат під знаком кореня. Ось як це робиться:
    • 6√(5)2 = 6√(5 x 5) = 6√25
    • 6√(2)3 = 6√(2 x 2 x 2) = 6√8
  6. Перемножте числа під знаком кореня: 6√(8 x 25)
  7. Запишіть відповідь. 6√(8 x 25) = 6√(200). У деяких випадках можна спростити підкорене вираз, наприклад, знайшовши множник числа 200, з якого можна взяти корінь 6 ступеня. Але в даному випадку вираз не спрощується.

Поради

  • Якщо "множник" відділяється від кореня знаком плюс або мінус, то це вже взагалі не множник — це окремий член виразу, і операції з ним проводяться окремо від кореня.
  • Знак кореня є ще одним способом запису дрібних показників. Наприклад, Квадратний корінь з будь-якого числа є це число в ступені 1/2; кубічний корінь з будь-якого числа є це число в ступені 1/3 і так далі.
  • Множник-число, що стоїть безпосередньо перед знаком кореня. Так, наприклад, у виразі 2 (квадратний корінь)5, число 5 є підкореним виразом, а число 2 — множником. Коли множник і корінь записані поруч, то це означає їх множення: 2*(квадратний корінь)5.

Джерела

  1. Http://www.purplemath.com/modules/radicals.htm
  2. Http://www.regentsprep.org/Regents/math/ALGEBRA/AO1/Lmultdiv.htm
  3. Http://www.ditutor.com/real_numbers/multiplication_radicals.html
  4. Http://www.themathpage.com/alg/multiply-radicals.htm

Ще почитати: