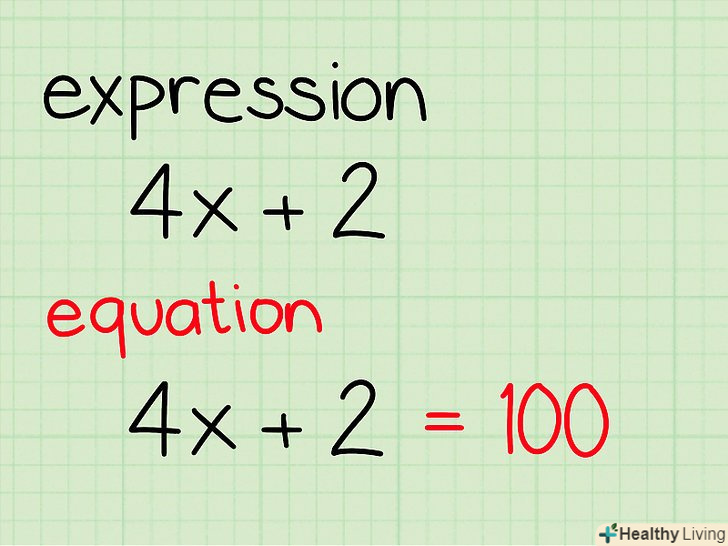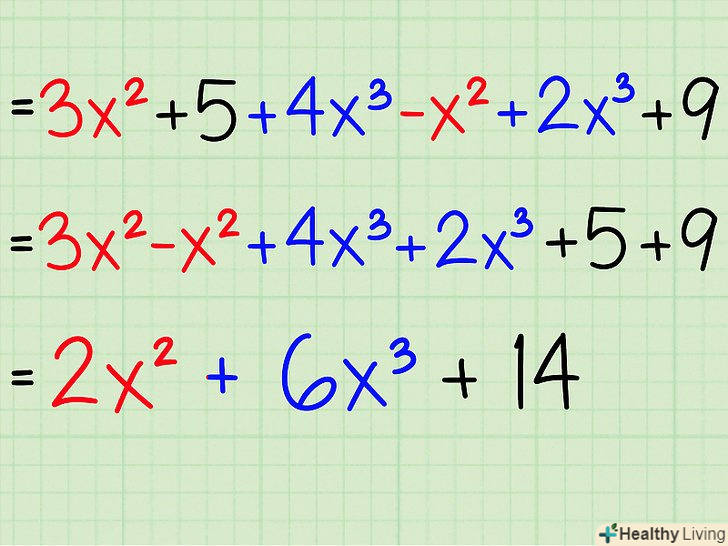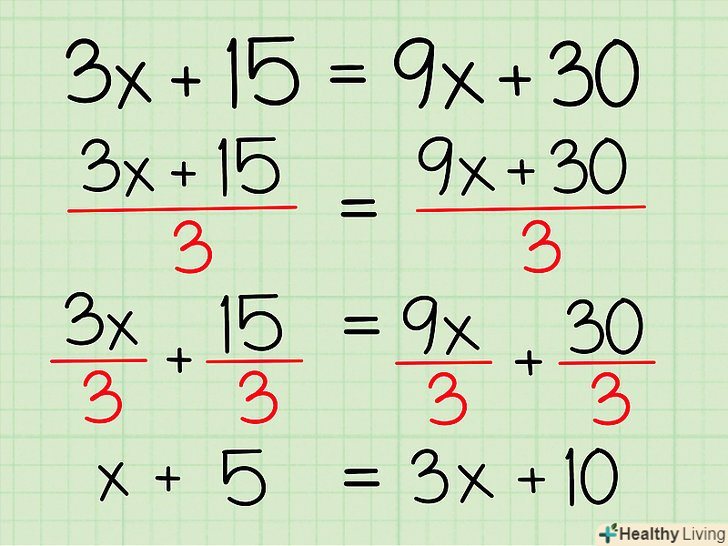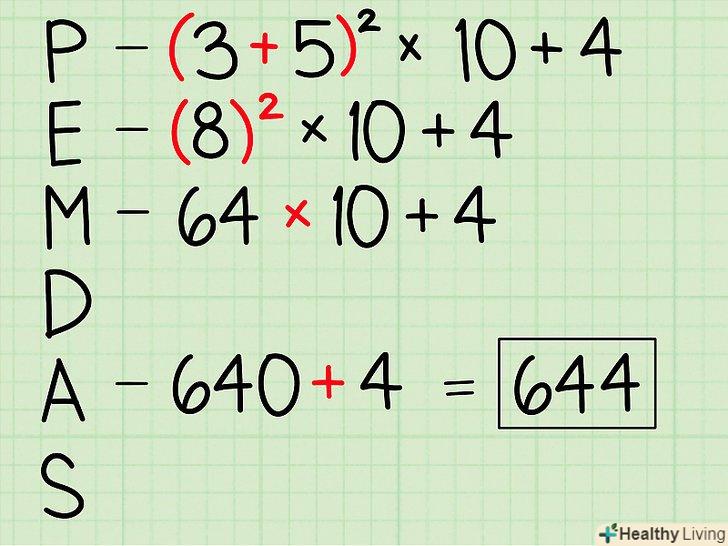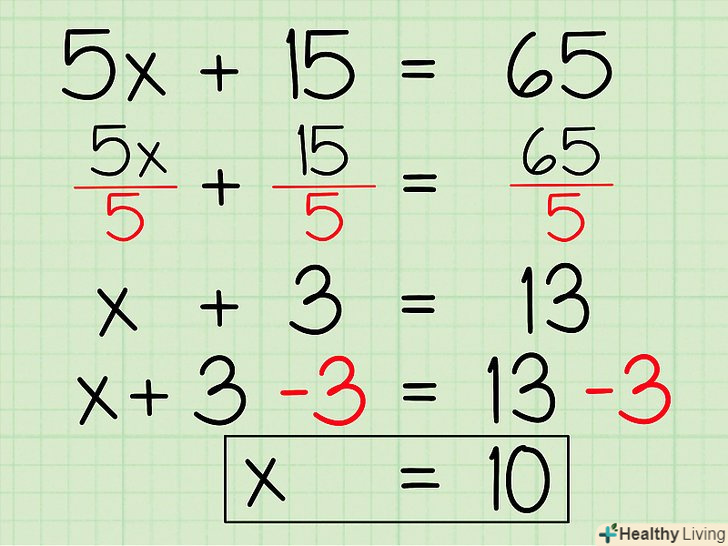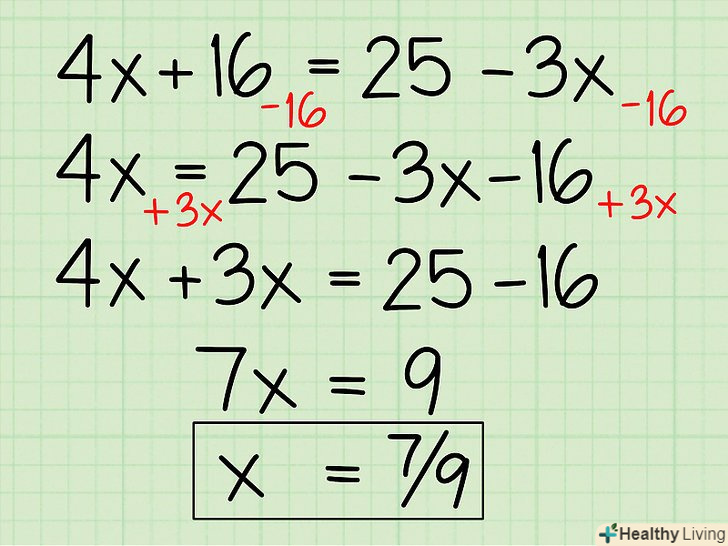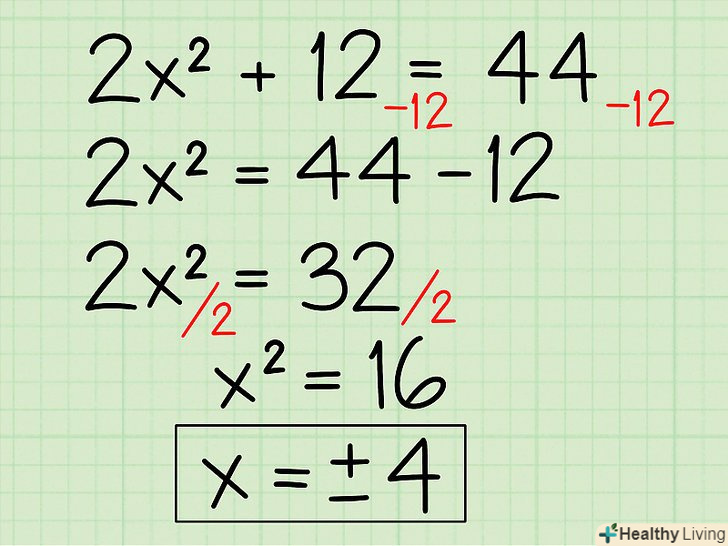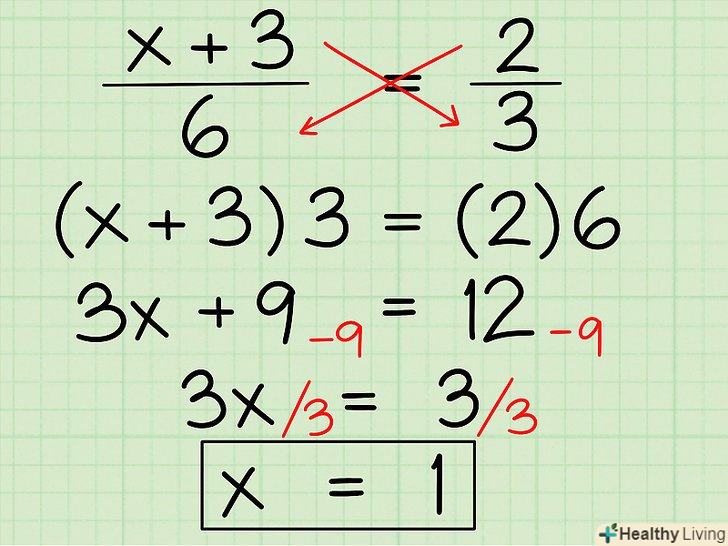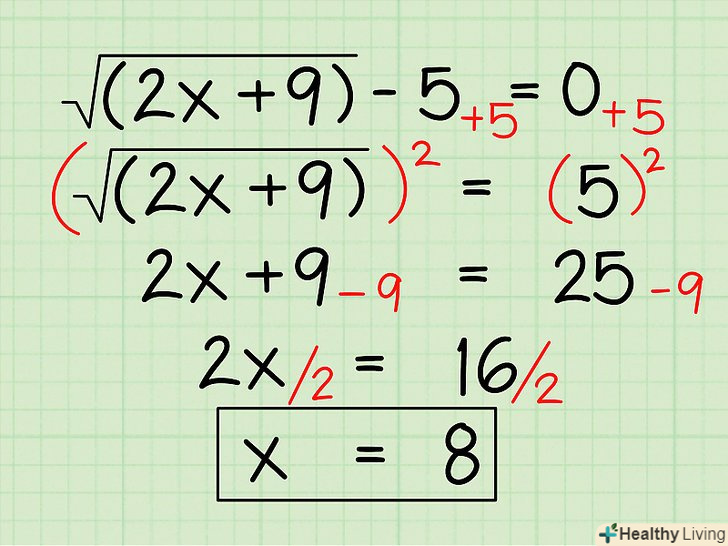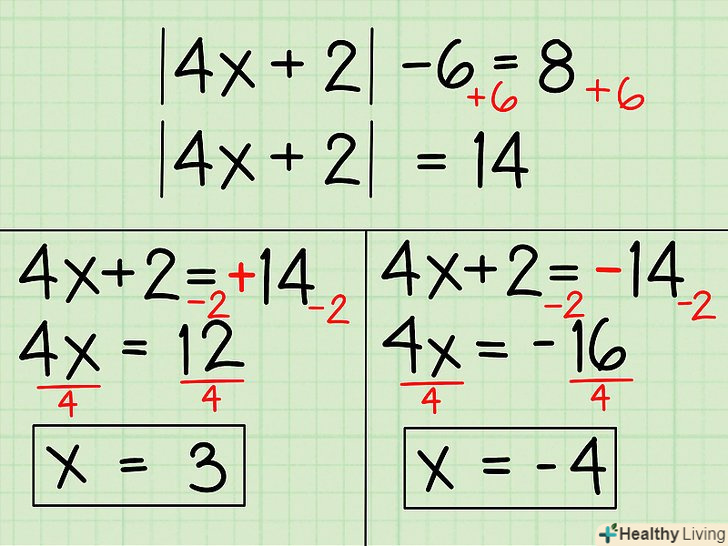Як розв'язувати алгебраїчні вирази: 10 кроків

Алгебраїчний вираз - це ряд чисел і змінних, об'єднаних математичними операціями (складанням, відніманням, множенням і т.д.). Так як алгебраїчний вираз ні до чого не прирівнюється, рішення виразу зводиться до його спрощення. Повноцінне рішення можливе для алгебраїчних рівнянь, які є алгебраїчними виразами, прирівняними до числа або до іншого виразу.

Частина1 З 2:

Основи

Визначення алгебраїчного виразу і алгебраїчного рівняння і різниця між ними.алгебраїчний вираз-це ряд чисел і змінних, об'єднаних математичними операціями (складанням, відніманням, множенням і т.д.). Воно ні до чого не прирівнюється і його рішення зводиться до його спрощення. Алгебраїчне рівняння є алгебраїчним виразом, прирівняним до числа або до іншого виразу, і для нього можливе повноцінне рішення. Ось кілька прикладів:
- Алгебраїчний вираз: 4x + 2
- Алгебраїчне рівняння: 4x + 2 = 100
Навчіться приводити подібні члени.це означає Скласти або відняти члени одного порядку. Тобто члени зі змінною x² можуть бути складені разом або відняті один з одного, члени зі змінною x³ можуть бути складені разом або відняті один з одного, і вільні члени (члени без змінної) можуть бути складені разом або відняті один з одного. Наприклад:
- 3x² + 5 + 4x³ - x² + 2x³ + 9 =
- 3x² - x² + 4x³ + 2x³ + 5 + 9 =
- 2x² + 6x³ + 14
Навчіться виносити множник за дужки. якщо вам дано алгебраїчне рівняння, тобто існують вирази з обох сторін від знака рівності, ви можете спростити рівняння, винісши множник за дужки. Розгляньте коефіцієнти всіх членів рівняння (коефіцієнт – це число, що стоїть перед змінною або взагалі не містить змінну) і знайдіть таке число, на яке діляться всі коефіцієнти. Ви можете винести це число за дужки і, таким чином, спростити рівняння. Ось як це робиться:
- 3x + 15 = 9x + 30
  - Тут кожен коефіцієнт ділиться на 3. Винесіть це число за дужки, розділивши кожен член на 3. Потім розділіть обидві частини рівняння на 3, щоб скоротити винесені за дужки 3.
- 3 (x + 5) = 3 (3х + 10)
- Х + 5 = 3x + 10
Запам'ятайте порядок виконання математичних операцій: дужки, ступінь, множення, ділення, додавання, віднімання. Ось приклад того, як дотримуватися порядку операцій:
- (3 + 5)² x 10 + 4
- Спочатку виконайте операцію в дужках:
- = (8)² x 10 + 4
- Потім зведіть в ступінь:
- = 64 х 10 + 4
- Далі помножте:
- = 640 + 4
- І, нарешті, складіть:
- = 644
Навчіться обґрунтовувати змінну. при вирішенні алгебраїчного рівняння ви повинні відокремити змінну (найбільш часто позначається як "х") на одній стороні рівняння. Ви можете відокремити змінну через ділення, множення, додавання, віднімання, Витяг кореня або інші операції. Після того, як ви відокремили «х», ви вирішили рівняння. Ось як це робиться:
- 5x + 15 = 65
- 5(x + 3) = 65
- Х + 3 = 13
- Х = 13 – 3
- Х = 10

Частина2 З 2:

Розв'язок алгебраїчних рівнянь

Вирішіть лінійне алгебраїчне рівняння.Лінійні алгебраїчні рівняння включають вільні члени і змінні першого ступеня. Для вирішення таких рівнянь використовуйте операції множення, ділення, додавання і віднімання, щоб відокремити змінну «х». Ось як це робиться:
- 4x + 16 = 25 - 3x
- 4x = 25 -16 - 3x
- 4x + 3x = 25 -16
- 7x = 9
- 7x/7 = 9/7 =
- Х = 9/7
Вирішіть алгебраїчне рівняння зі змінною другого порядку.у такому рівнянні необхідно відокремити змінну, а потім витягти квадратний корінь одночасно зі змінної і з виразу на іншій стороні рівняння. Ось як це робиться:
- 2x² + 12 = 44
  - По-перше, перенесіть 12 на іншу сторону рівняння.
- 2x² = 44 -12
- 2x² = 32
  - Тепер розділіть обидві частини рівняння на 2.
- 2x²/2 = 32/2
- X² = 16
  - Вийміть квадратний корінь з виразів, що знаходяться з обох сторін рівняння.
- √x² = √16
- X1 = 4; х2 = -4
Вирішіть алгебраїчне рівняння з дробами.для цього скористайтеся множенням хрест-навхрест, приведіть подібні члени, а потім відокремте змінну. Ось як це робиться:
- (х + 3) / 6 = 2/3
  - По-перше, скористайтеся множенням хрест-навхрест, щоб позбутися від дробів. Тобто ви повинні помножити чисельники на знаменники.
- (х + 3) х 3 = 2 х 6 =
- 3x + 9 = 12
  - Тепер приведіть подібні члени. Приведіть вільні члени 9 і 12, перенісши 9 на іншу сторону рівняння.
- 3x = 12 - 9
- 3x = 3
  - Відокремте змінну "х", розділивши обидві сторони рівняння на 3.
- 3x/3 = 3/3
- Х = 3
Вирішіть алгебраїчне рівняння з коренем.для цього зведіть вирази, що знаходяться з обох сторін рівняння, в квадрат. Ось як це робиться:
- √(2x +9) - 5 = 0
  - По-перше, перенесіть члени, що стоять поза коренем, на іншу сторону рівняння:
- √(2x +9) = 5
- Потім зведіть в квадрат виразу, що знаходяться з обох сторін рівняння (щоб позбутися від кореня):
- (√(2x+9))² = 5²
- 2x + 9 = 25
  - Тепер приведіть подібні члени і відокремте змінну.
- 2x = 25 - 9
- 2x = 16
- X = 8
Вирішіть алгебраїчне рівняння, що містить абсолютні величини.абсолютна величина числа-це його невід'ємне значення. Наприклад, абсолютне значення -3 (позначається як |3|) дорівнює 3. Для вирішення таких рівнянь відокремте абсолютне значення і знайдіть два значення «х» - одне значення при позитивному значенні виразу, укладеному в вертикальні дужки, а інше значення при негативному значенні виразу, укладеному в вертикальні дужки. Ось як це зробити:
- Спочатку відокремте абсолютну величину, а потім опустіть вертикальні дужки. Зараз ви знайдете " х " при позитивному значенні виразу, укладеному в вертикальні дужки:
  - |4x +2| - 6 = 8
- |4x +2| = 8 + 6
- |4x +2| = 14
- 4x + 2 = 14
- 4x = 12
- X = 3
  - Тепер ви знайдете " х " при негативному значенні виразу, укладеному в вертикальні дужки. Для цього змініть знак виразу, що стоїть праворуч від знака рівності, на негативний:
- |4x +2| = 14
- 4x + 2 = -14
- 4x = -14 -2
- 4x = -16
- 4x/4 = -16/4
- X = -4
  - Запишіть обидві відповіді: х1 = 3, х2 = -4

Поради

Для перевірки відповіді відкрийте сайт wolfram-alpha.com.
Для перевірки відповіді підставте знайдене значення у вихідне рівняння. Якщо рівність дотримано, то рівняння вирішено правильно.