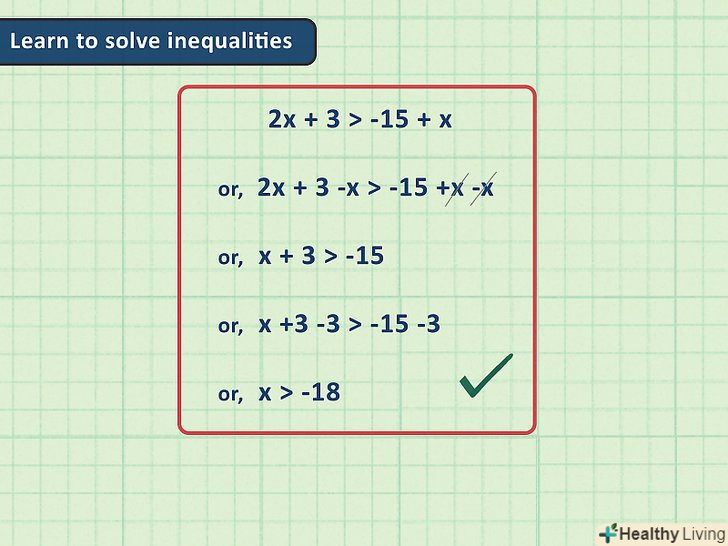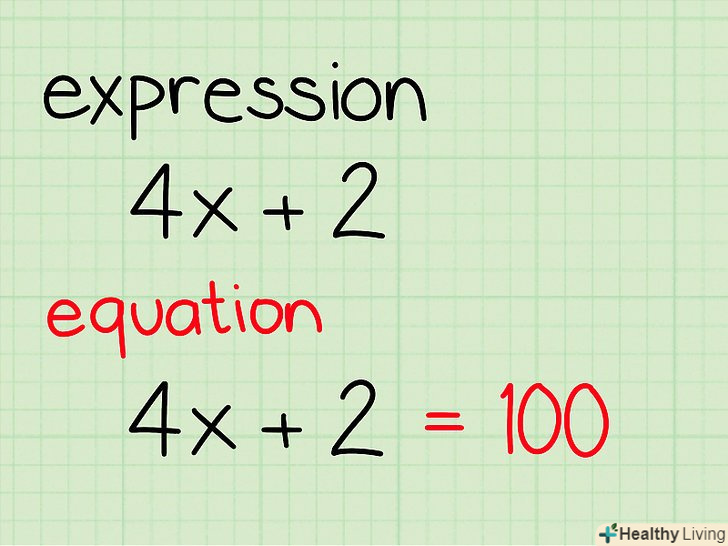Як вивчати алгебру ( з ілюстраціями)

Освоївши алгебру, Ви зможете вивчати інші математичні дисципліни, кожна з яких ґрунтується на деяких базисних принципах і навичках. Освоєння таких навичок може стати нелегким завданням для тих, хто вперше стикається з математикою. Якщо це ваш випадок, не нервуйте – прочитайте цю статтю, в якій наводяться пояснення, приклади та поради, завдяки яким ви зможете вирішувати завдання як досвідчений математик.

Частина1З 5:

Основні алгебраїчні правила

Основні математичні операції.для початку освойте основні математичні операції: додавання, віднімання, множення і ділення. Це перший крок на шляху вивчення алгебри. Якщо ви не засвоїте ці операції, вам буде складно вивчати більш складні алгебраїчні концепції. Рекомендуємо вам прочитати статтю як вивчати математику.
- Не обов'язково виконувати математичні операції в розумі. У більшості випадків вам буде дозволено користуватися калькулятором. Але краще засвоїти принципи виконання математичних операцій вручну на випадок, якщо ви не зможете скористатися калькулятором.
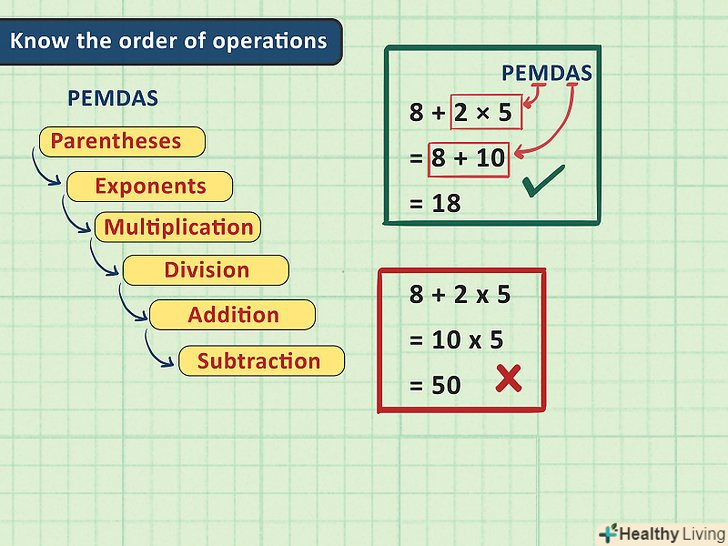
Запам'ятайте правильний порядок виконання операцій: виконайте вираз в дужках, зведіть в ступінь, помножте, розділіть, складіть, відніміть. Ще раз наведемо правильний порядок виконання математичних операцій:
- Вираз у дужках
- Зведення в ступінь
- Множення
- Поділ
- Додавання
- Віднімання
- Порядок виконання операцій має важливе значення, тому що виконання операцій не в тому порядку призведе до неправильного результату. Наприклад, якщо дано вираз 8 + 2 х 5, то склавши 8 і 2, Ви отримаєте 10 х 5 = 50. А якщо ви спочатку перемножите 2 і 5, то отримаєте 8 + 10 = 18. Другий результат є вірним, а перший ні.
Навчіться працювати з негативними числами. в алгебрі використовуються негативні числа, тому необхідно знати, як їх складати, віднімати, множити і ділити. Нижче наведені деякі основні принципи роботи з негативними числами.
- На числовій прямій негативне число розташоване на такій же відстані від нуля, що і рівне йому за значенням позитивне число (але в протилежному напрямку).
- При додаванні двох негативних чисел ви отримаєте менше негативне число (по модулю результат буде більше модулів двох складаються чисел, а за фактом менше, так як це негативні числа).
- При відніманні негативного числа ви можете замінити два знаки "мінус «на знак» плюс", тобто ви додасте позитивне число.
- При перемноженні або діленні двох негативних чисел ви отримаєте позитивний результат.
- При перемноженні або діленні позитивного числа і негативного числа Ви отримаєте негативний результат.
Рішення довгих виразів.на відміну від коротких виразів для вирішення довгих виразів може знадобитися безліч кроків. Щоб уникнути помилок кожен крок рішення пишіть на новому рядку. Якщо ви вирішуєте рівняння, спробуйте писати знаки рівності один під одним. Так вам буде простіше знайти і виправити помилку.
- Наприклад, дано вираз 9/3 - 5 + 3 х 4. Вирішіть його наступним чином:
  
  9/3 - 5 + 3 × 4
  
  9/3 - 5 + 12
  
  3 - 5 + 12
  
  3 + 7
  
  10

Частина2З 5:

Змінні

Змінні позначаються літерами.у деяких алгебраїчних виразах поряд з числами ви зустрінете і змінні. Працювати зі змінними не так складно, як здається – вони просто позначають величини, значення яких не відомі. Нижче наведені приклади змінних:
- Літери латинського алфавіту: x, y, z, a, b, C
- Літери грецького алфавіту, наприклад, θ
- Зверніть увагу, що не всі літери позначають змінні. Наприклад, буква π позначає число Пі, значення якого відомо (3,1459).
Пам'ятайте, що змінні-це величини, значення яких не відомі.тобто теоретично існує число (або кілька чисел), яке може бути підставлено замість змінної. Найчастіше основною метою вирішення алгебраїчних рівнянь є знаходження значення змінної.
- Наприклад, в рівнянні 2х + 3 = 11» х " – це змінна. Це означає, що існує таке значення "х", при якому ліва сторона рівняння буде дорівнює 11. Так як 2 х 4 + 3 = 11, то х = 4.
- Для кращого з'ясування змінних в рівняннях міняйте їх на знак питання. Наприклад, рівняння 2 + 3 + х = 9 можна переписати у вигляді 2 + 3+? = 9; таким чином, потрібно з'ясувати, яке число слід додати до 2 + 3, щоб отримати 9. Таким числом є число 4.
Якщо у виразі змінна присутня в декількох членах, то такий вираз можна спростити. для цього складіть або відніміть подібні члени, тобто члени з однаковою змінною (при цьому у однакових змінних повинен бути однаковий показник ступеня). Це не так складно, як здається. Наприклад, х + х = 2х, але х + у ≈ 2XY.
- Наприклад, розглянемо рівняння 2x + 1x = 9. В цьому випадку складіть 2х і 1х: 2х+1х = 3х, тобто початкове рівняння переписується у вигляді 3х = 9. Таким чином, х = 3.
- Ще раз: складаються і віднімаються члени з однаковими змінними. У рівнянні 2х + 1y = 9 ви не можете скласти 2x і 1y, тому що в цих членах різні змінні.
- Також пам'ятайте, що у однакових змінних повинен бути однаковий показник ступеня. Наприклад, у рівнянні 2x + 3x² = 10 ви не можете скласти 2x і 3x² через різні показники ступеня. Рекомендуємо прочитати статтю як складати ступені.

Частина3З 5:

Рішення найпростіших рівнянь

Для вирішення рівняння відокремте змінну на одній стороні рівняння.рішення алгебраїчного рівняння-це знаходження значення змінної. Тому необхідно відокремити змінну на одній стороні рівняння, а числа – на іншій стороні. Наприклад, розглянемо рівняння х + 2 = 9 х 4.
- У нашому прикладі для відокремлення змінної " х " необхідно перенести 2 на праву сторону рівняння. Для цього з обох частин рівняння відніміть 2 (щоб Значення рівняння не змінилося). Ви отримаєте х = 9 х 4 – 2 = 36 - 2 = 34.
При перенесенні числа через знак рівності математична операція змінюється на протилежну – тут розглянемо операції додавання і віднімання.для відокремлення змінної на одній стороні рівняння необхідно перенести число за знак рівності. Для цього необхідно відняти або прибувати це число до обох сторін рівняння. Наприклад, розглянемо рівняння х + 3 = 0. Тут необхідно перенести 3 за знак рівності. Для цього потрібно відняти 3 від обох сторін рівняння, тобто написати так: х + 3 - 3 = 0 - 3. Таким чином, ви отримаєте х = -3.

Запам'ятайте: якщо число додається, відніміть його на іншій стороні рівняння; якщо число віднімається, додайте його на іншій стороні рівняння.

число, що додається віднімайте. Наприклад, х + 9 = 3; х = 3 - 9

віднімається число додавайте. Наприклад, х - 4 = 20; х = 20 + 4
При перенесенні числа через знак рівності математична операція змінюється на протилежну – тут розглянемо операції множення і ділення.наприклад, якщо змінна множиться на 3, то розділіть обидві сторони рівняння на 3.

Запам'ятайте: якщо змінна множиться на число, діліть на нього іншу сторону рівняння; якщо змінна ділиться на число, помножте на нього іншу сторону рівняння.

множення міняйте на ділення. Наприклад, 6x = 14 + 2; x = (14 + 2)/6

поділ міняйте на множення. Наприклад, x/5 = 25; x = 25 × 5
При перенесенні числа через знак рівності математична операція змінюється на протилежну – тут розглянемо зведення в ступінь і витяг кореня. рекомендуємо прочитати статтю як вирішувати вирази зі ступенями. Операцією, протилежною зведенню в ступінь, є витяг кореня (і навпаки). Наприклад, операцією, протилежної зведенню в квадрат (в другу ступінь), є витяг квадратного кореня (√); операцією, протилежною зведенню в куб (в третю ступінь), є витяг кубічного кореня (³√).
- Якщо змінна зводиться до ступеня, витягніть корінь з обох сторін рівняння. Якщо змінна стоїть під знаком кореня, зведіть в ступінь обидві сторони рівняння.
  
  у разі зведення в ступінь витягайте корінь. Наприклад, x² = 49; x = √49
  
  у разі вилучення кореня зводите в ступінь. Наприклад, √x = 12; x = 12²

Частина4З 5:

Відточування навичок

Якщо ви не можете визначити, як вирішити дане вам рівняння, візуалізуйте його за допомогою картинок або діаграм.або ж візьміть кілька предметів, наприклад, кубики або монети (якщо є).
- Наприклад, вирішимо рівняння х + 2 = 3, скориставшись значком ☐.
  
  x +2 = 3
  
  ☒+☐☐ =☐☐☐
  
  з обох сторін рівняння відніміть 2. Для цього з кожного боку рівняння приберіть по два значка ( ☐ ☐ ):
  
  ☒+☐☐-☐☐ =☐☐☐-☐☐
  
  ☒=☐, тобто x = 1
- Інший приклад 2x = 4.
  
  ☒☒ =☐☐☐☐
  
  обидві сторони рівняння розділіть на 2. Для цього розділіть значки на дві рівні групи з обох сторін рівняння.
  
  ☒|☒ =☐☐|☐☐
  
  ☒ =☐ ☐, тобто x = 2
При вирішенні задачі перевіряйте складене вами рівняння.для цього замість змінної підставте найпростіші значення, наприклад, х = 0, або х = 1, або х = -1, і з'ясуйте, чи має рівняння сенс. Наприклад, легко помилитися і написати р = 6D, тоді як потрібно написати р = d/6.
- Наприклад, дана така задача: довжина футбольного поля більше його ширини на 30 м.складіть наступне рівняння: l = w + 30. Перевірте, чи має це рівняння сенс; для цього замість змінних підставте деякі значення. Наприклад, якщо ширина w = 10 м, то довжина поля l = 10 + 30 = 40 м; якщо ширина w = 30 м, то довжина поля l = 30 + 30 = 60 м (і так далі). Це рівняння має сенс, так як при будь-якому значенні ширини довжина виходить більше.
Пам'ятайте, що відповіді (кінцеві значення) не завжди будуть цілими числами.вони можуть бути десятковими дробами, звичайними дробами або ірраціональними числами. Такі відповіді знаходяться за допомогою калькулятора, але ваш викладач може зажадати вказати відповідь в іншому вигляді.
- Наприклад, ви отримали відповідь х = 1250⁷. За допомогою калькулятора зведіть 1250 в сьому ступінь, і ви отримаєте величезне число. В цьому випадку краще записати відповідь у вигляді х = 1250⁷ або ж в експоненціальному поданні.
Вивчивши основи алгебри, переходите до розкладання многочленів на множники.це вельми просунута техніка, яка дозволить вам представляти складні многочлени в спрощеному вигляді. Рекомендуємо прочитати цю статтю. Нижче наведено кілька порад щодо розкладання многочленів на множники.
- Многочлени виду ax + ba розкладаються на множники a(x + b). Наприклад: 2x + 4 = 2 (x + 2)
- Многочлени виду ax² + bx розкладаються на множники cx((a/c)x + (b/c)), де c – найбільше число, на яке націлено діляться a і b. наприклад: 3y² + 12Y = 3Y (y + 4)
- Многочлени виду x² + bx + c розкладаються на множники (x + y)(x + z), де YX z = c і yx + zx = bx. Наприклад: x² + 4x + 3 = (x + 3)(x + 1).
Більше практикуйтеся у вирішенні рівнянь і задач.тільки так ви освоїте алгебраїчні навички. Не хвилюйтеся - уважно слухайте вчителя, виконуйте домашнє завдання і, якщо необхідно, просите допомоги у вчителя або ваших однокласників.
Задавайте питання вчителю, якщо ви щось не розумієте.ви не зобов'язані самостійно розбиратися в тонкощах алгебри, тому задавайте питання Вашому викладачеві. Підійдіть до нього після уроку і ввічливо задайте питання. Хороший учитель з готовністю пояснить вам незрозумілі моменти (швидше за все, після уроків) і покаже, як вирішувати завдання.
- Якщо з будь-якої причини Ваш вчитель не може допомогти вам, спробуйте отримати пояснення якось по-іншому. Наприклад, в деяких школах існують факультативи, які проводяться після занять і на яких ви зможете знайти відповіді на ваші запитання. Пам'ятайте, що не варто соромитися просити про допомогу – це свідчить про вашу зацікавленість у вивченні предмета.

Частина5 З 5:

Вивчення інших тем

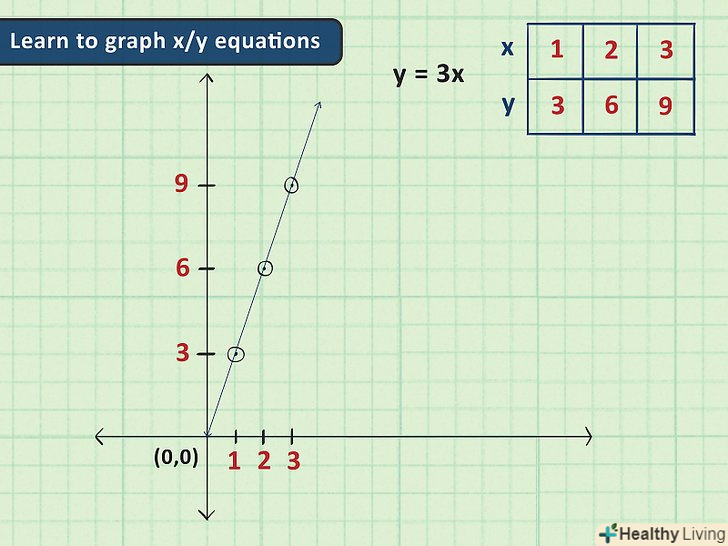
Побудова графіка функції (рівняння зі змінними х і у).графіки є важливою складовою алгебри, тому що вони дозволяють візуалізувати інформацію, представлену числами. У більшості випадків потрібно побудувати графік рівняння з двома змінними (х і у); це робиться на двовимірній площині координат, представленої осями Х і Y. Для побудови графіка замість змінної х» підставте певні значення, щоб знайти значення змінної «у» (або навпаки); так ви отримаєте парні значення, які є координатами точок графіка.
- Наприклад, дано рівняння у = 3x. підставте в нього х = 2 і отримаєте у = 6, тобто ви отримали точку з координатами (2,6) (два по осі X і шість по осі Y).
- Рівняння виду у = мх + b ( де m і b – це числа) є найпоширенішими алгебраїчними рівняннями. Кутовий коефіцієнт графіка цього рівняння дорівнює m, і графік перетинає вісь Y при у = b.
Рішення нерівностей.у нерівностях замість знака рівності стоїть один із знаків нерівностей. Нерівності зі знаками &#gt; (більше) і &#lt; (менше) вирішуються аналогічно звичайним рівностям. В результаті ви отримаєте змінну, більшу або меншу певного значення.
- Наприклад, розглянемо нерівність 3 &#gt; 5x-2.
  
  3 &#gt; 5x - 2
  
  5 &#gt; 5x
  
  1 &#gt; x або X &#lt; 1.
- Це означає, що змінна " х " приймає будь-яке значення, менше 1. Тобто змінна " х " може бути рівною 0, -1, -2 і так далі. Якщо підставити ці значення в початкове нерівність, Ви отримаєте відповідь, менший 3.
Рішення квадратних рівнянь. це рівняння виду ax² + bx + c = 0, де a, b, c – числа, причому «а» може дорівнювати нулю, а «b» і «c» не можуть дорівнювати нулю. Такі рівняння вирішуються за формулою x = [- b + / - √(b² - 4ac)]/2a. зверніть увагу на те, що знак +/- вказує на можливість наявності двох коренів.
- Наприклад, розглянемо квадратне рівняння 3x² + 2x -1 = 0.
  
  x = [-b +/- √(b² - 4ac)]/2a
  
  x = [-2 +/- √(2² - 4(3)(-1))]/2(3)
  
  x = [-2 +/- √(4 - (-12))]/6
  
  x = [-2 +/- √(16)]/6
  
  x = [-2 +/- 4]/6
  
  x1 = -1 і х2 = 1/3
Рішення систем рівнянь.система рівнянь включає в себе кілька рівнянь. Вирішувати системи рівнянь не так складно, як здається. Багато викладачів вимагають вирішувати системи рівнянь за допомогою графіків. Якщо система рівнянь включає два рівняння, то рішенням системи є координати точок перетину графіків двох рівнянь.
- Наприклад, дана система рівнянь у = 3x-2 і у = - х-6. Якщо ви побудуєте графіки обох рівнянь, ви отримаєте зростаючу пряму і спадаючу пряму, які перетнуться в точці з координатами (-1, -5). Це і є рішення системи рівнянь.^{[1]X
  Джерело інформації}
- Якщо ви хочете перевірити відповідь, підставте знайдені значення в рівняння.
  
  y = 3x - 2
  
  -5 = 3(-1) - 2
  
  -5 = -3 - 2
  
  -5 = -5
  
  y = -x - 6
  
  -5 = -(-1) - 6
  
  -5 = 1 - 6
  
  -5 = -5
- Рівність дотримано!

Поради

В Інтернеті є безліч корисних ресурсів для людей, які вивчають алгебру. Для їх пошуку в пошуковику введіть щось на зразок "допомога з алгебри". Також ви знайдете сотні корисних статей з алгебри на сайті ru.wikihow.com.
Якщо ви зіткнулися з проблемами, відкрийте сайт videourokionline.ru або school-assistant.ru.Там ви знайдете поради та завдання з різних предметів, включаючи алгебру.
Пам'ятайте, що за допомогою краще звернутися до людей, яких Ви знаєте. Наприклад, зверніться до друзів або однокласників, якщо ви не зрозуміли тему останнього уроку з алгебри.