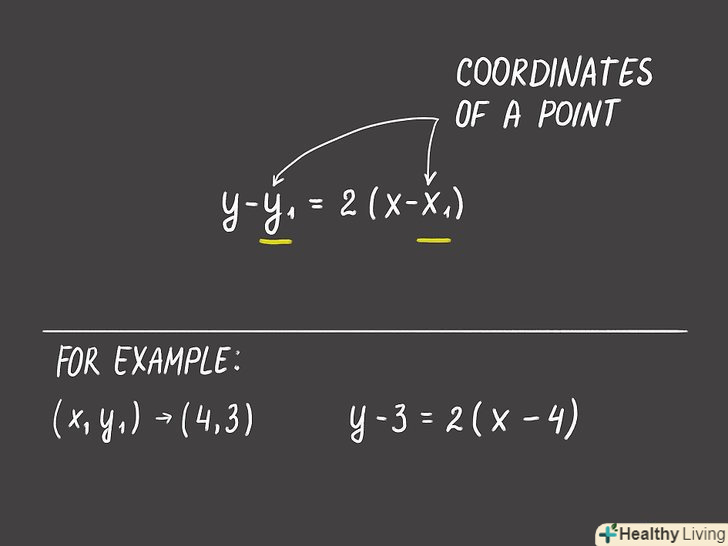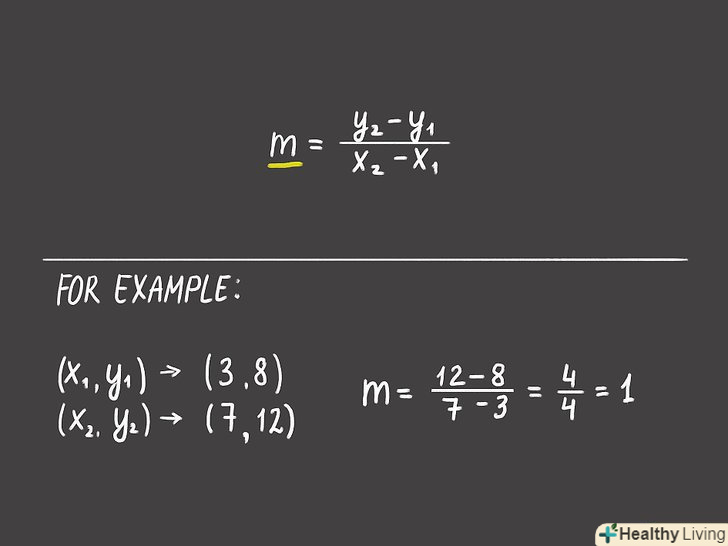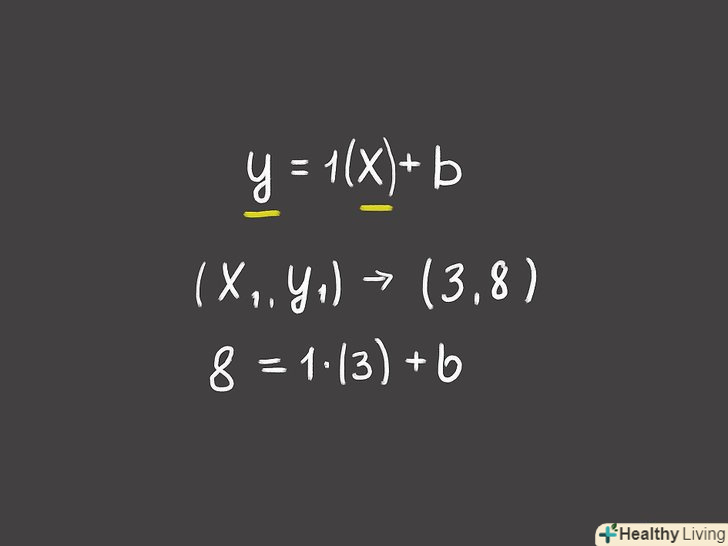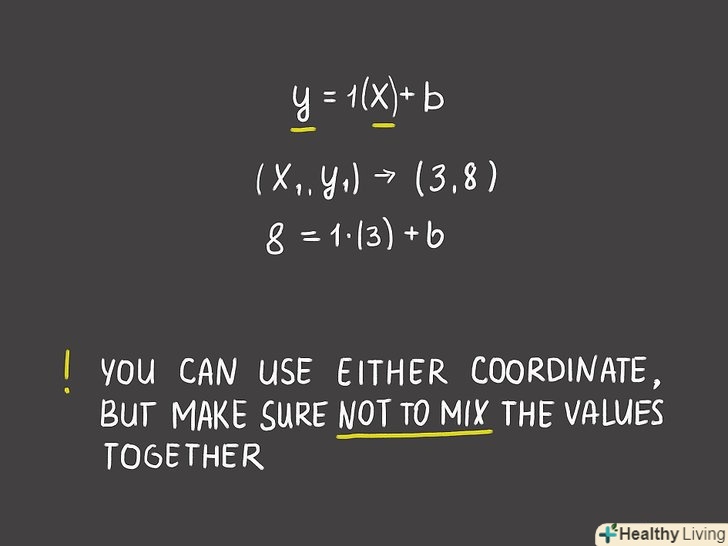1. Головна
    2. Геометрія
    3. Як знайти рівняння прямої: 8 кроків (з ілюстраціями)

Як знайти рівняння прямої: 8 кроків (з ілюстраціями)

У тригонометрії є задачі, в яких потрібно знайти рівняння прямої. При цьому дані або координати однієї точки і кутовий коефіцієнт, або координати двох точок, які лежать на прямій. У будь-якому випадку знайти рівняння прямої досить легко, якщо використовувати відповідні формули.

Метод1 З 2:
За координатами однієї точки та кутовим коефіцієнтом

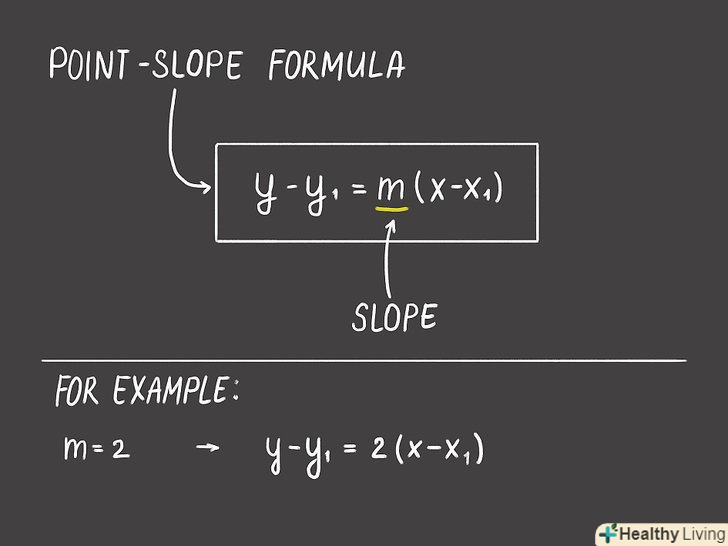
  1. Підставте значення кутового коефіцієнта " k " в альтернативне рівняння прямої y-y1 = k(x-x1). за допомогою цього рівняння, в якому присутні координати точки, яка лежить на прямій, можна знайти координати точки перетину прямої з віссю Oy. Дане значення кутового коефіцієнта "k «підставте замість» k" в рівнянні y-y1= k(x-x1).[1]
    • Наприклад, кутовий коефіцієнт k = 2, тоді рівняння запишеться так:Y-y1= 2 (x-x1).
  2. Замість x1 і y1 підставте координати даної точки, щоб записати остаточне рівняння прямої. [2]
    • Наприклад, якщо дана точка з координатами(4,3), рівняння запишеться так:Y-3 = 2 (x-4).
  3. Ізолюйте "y", щоб записати рівняння прямої в кінцевому вигляді. щоб розкрити дужки, застосуйте властивість дистрибутивності, а потім дотримуйтесь певного порядку виконання математичних операцій.
    • Розкривши дужки, Ви отримаєте: y-3 = 2x-8.
    • Тепер додайте 3 до кожної сторони рівняння, щоб ізолювати "y".
    • Остаточне рівняння прямої, яка проходить через точку з координатами (4, 3) і має кутовий коефіцієнт 2, запишеться так:Y = 2x-5.

Метод2 З 2:
За координатами двох точок

  1. Обчисліть кутовий коефіцієнт за формулоюk = (y2-y1)/(x2-x1 ). вам будуть дані дві пари координат; кожна пара координат записується так: (x, y). Першу пару координат позначте як (x1, y1), а другу як (x2, y2). Підставте числа в формулу k = (y2-y1)/(x2-x 1) і обчисліть кутовий коефіцієнт k.[3]
    • Наприклад, дані дві точки з координатами (3, 8) і (7, 12). Тоді формула запишеться так:k = (12-8)/(7-3) = 4/4 = 1. У цьому прикладі кутовий коефіцієнт k = 1.
  2. Підставте знайдене значення кутового коефіцієнтаk в стандартне рівняння прямої. рівняння прямої має наступний вигляд: y = k x + b, деk — кутовий коефіцієнт, b — координата «y» точки перетину прямої з віссю Oy. У рівняння прямої підставте знайдене значення кутового коефіцієнта замість "k".[4]
    • У нашому прикладі рівняння прямої запишеться так:Y = 1x + B або y = x + b.
  3. [5]
    • У нашому прикладі візьмемо точку з координатами (3, 8). Тоді рівняння прямої запишеться так:8 = 1(3) + B.
    • Використовуйте координати однієї з двох даних точок, але ніколи не змішуйте координати відразу двох точок.
  4. Обчисліть "b".зробіть це, коли в рівняння прямої підставите значення» k«,» х «і»у". Ізолюйте " b " на одній стороні рівняння, дотримуючись певного порядку виконання математичних операцій.[6]
    • У нашому прикладі рівняння прийняло вигляд 8 = 1(3) + B. помножте 1 на 3 і отримаєте 8 = 3 + B. Тепер відніміть 3 з кожної сторони рівняння, щоб ізолювати «b». Ви отримаєте 5 = B, абоB = 5.
  5. Підставте знайдені значення "k» і" b " в рівняння прямої, щоб записати його в остаточному вигляді.
    • У нашому прикладі рівняння прямої, яка проходить через точки з координатами (3, 8) і (7, 12), запишеться так:Y = 1x + 5 або просто Y = x + 5.

Джерела

  1. ↑ Http://www.coolmath.com/algebra/08-lines/11-finding-equation-line-point-slope-01
  2. ↑ Http://www.coolmath.com/algebra/08-lines/11-finding-equation-line-point-slope-01
  3. ↑ Http://www.coolmath.com/algebra/08-lines/12-finding-equation-two-points-01
  4. ↑ Https://www.mathwarehouse.com/algebra/linear_equation/write-equation/equation-of-line-given-two-points.php
  5. ↑ Https://www.mathwarehouse.com/algebra/linear_equation/write-equation/equation-of-line-given-two-points.php
  6. ↑ Https://www.mathwarehouse.com/algebra/linear_equation/write-equation/equation-of-line-given-two-points.php

Ще почитати: