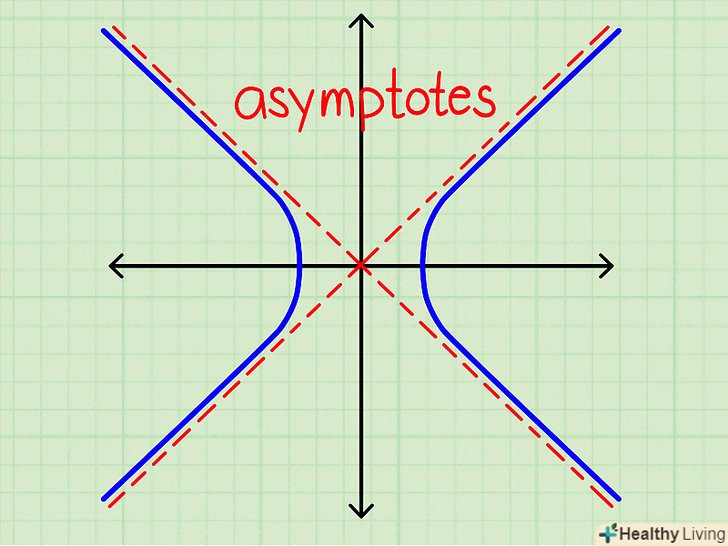
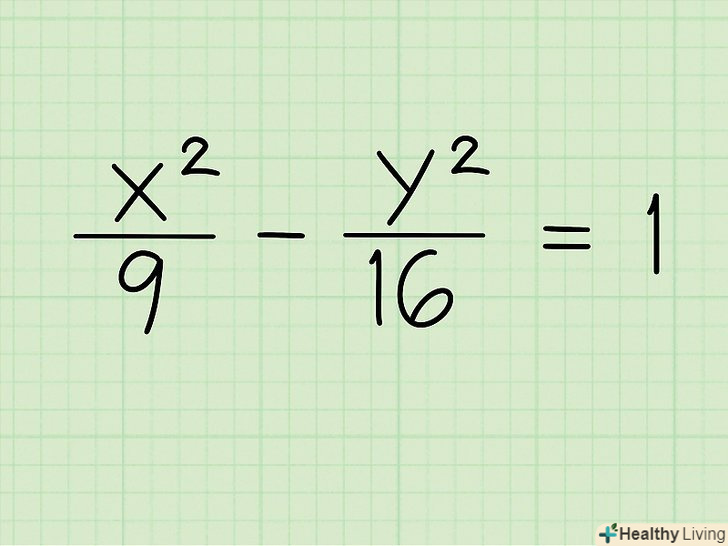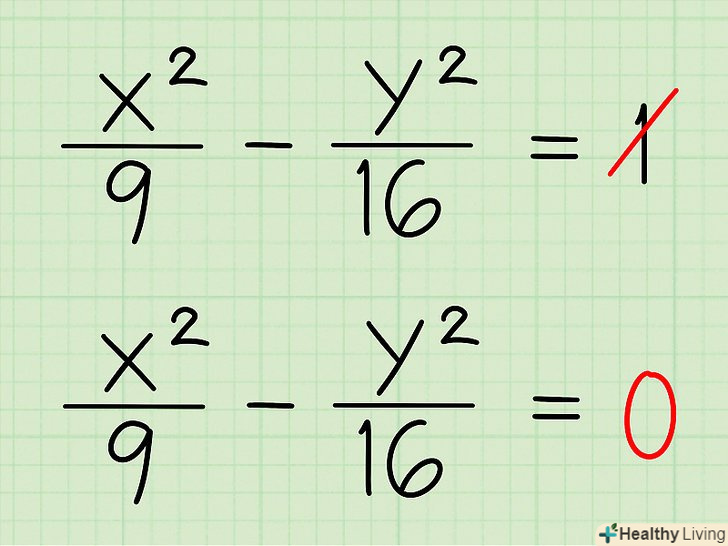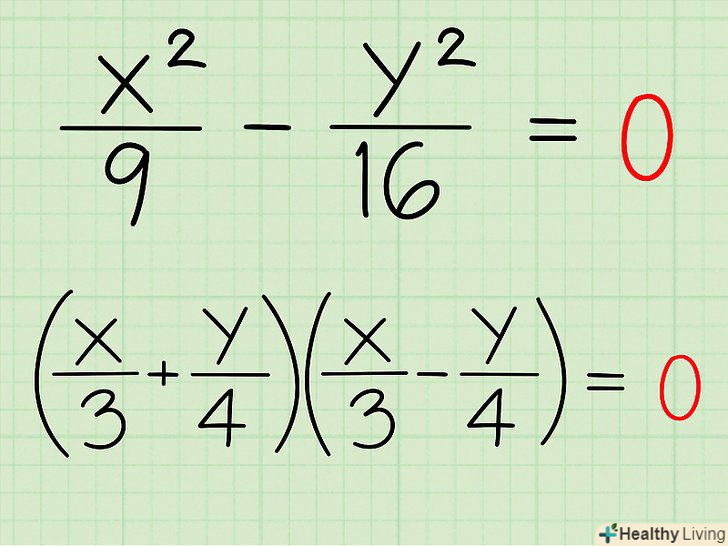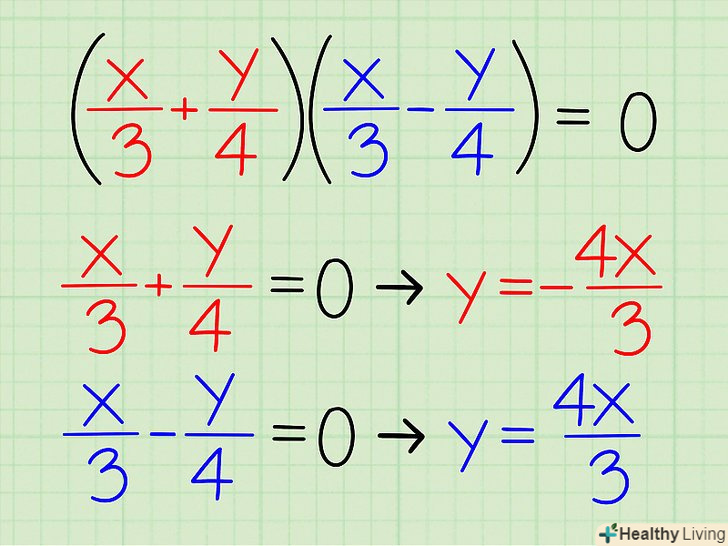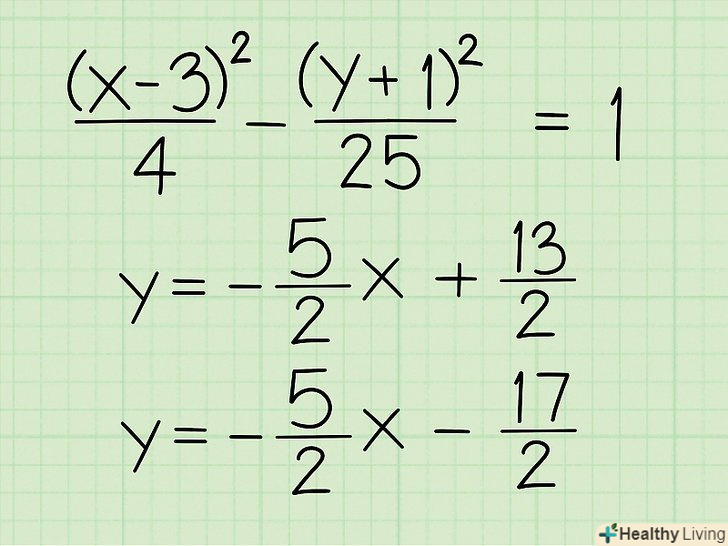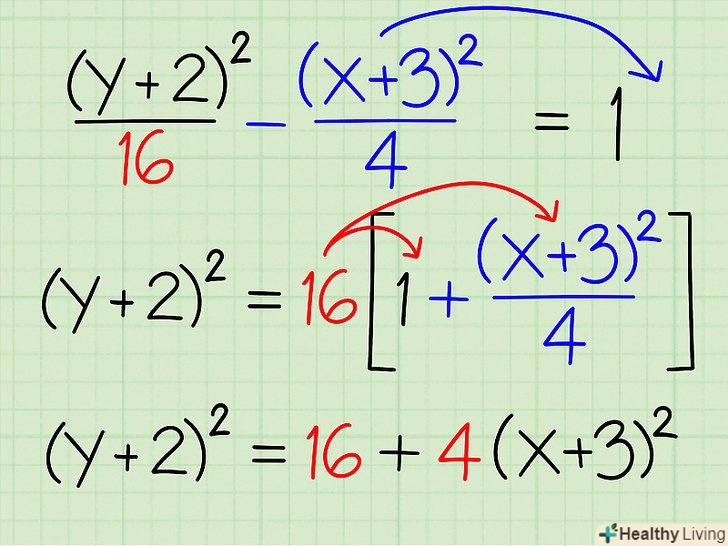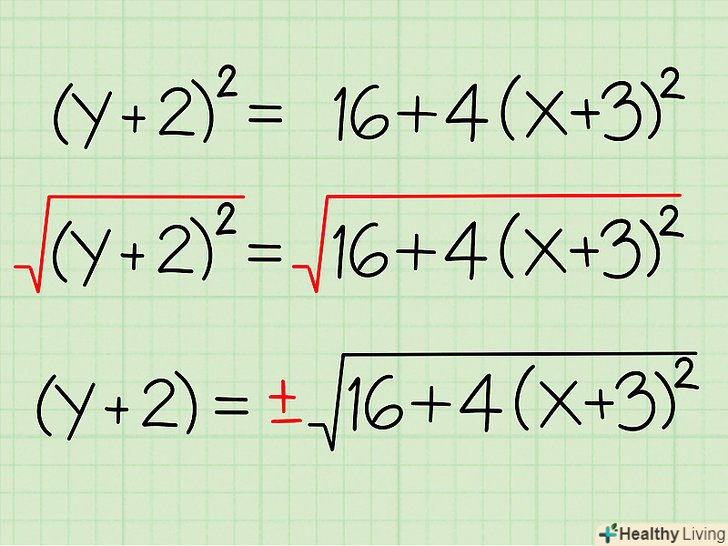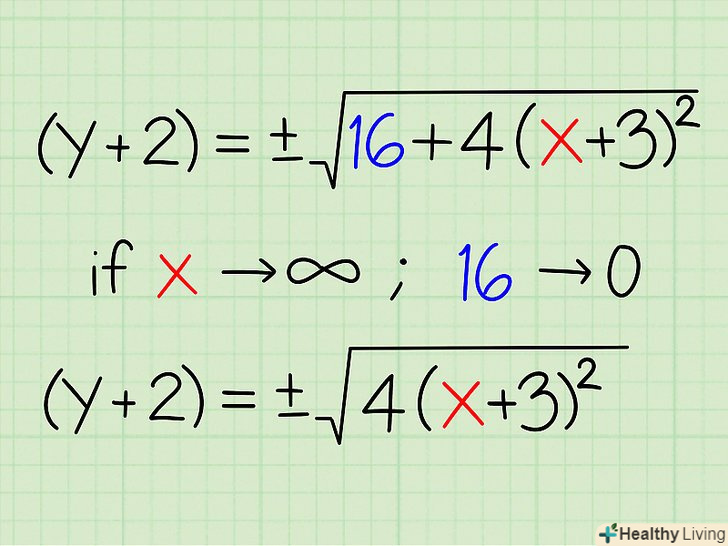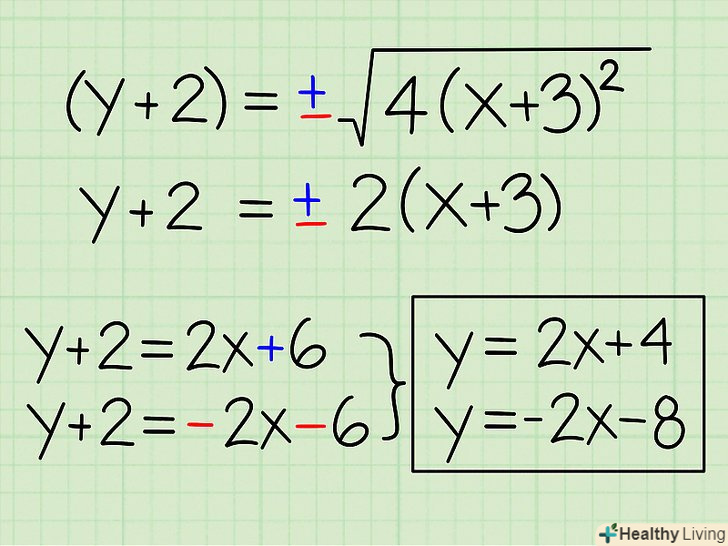Як знайти рівняння асимптот гіперболи: 10 кроків

Асимптоти гіперболи-це прямі, що проходять через центр гіперболи. Гіпербола наближається до асимптотам, але ніколи не перетинає (і навіть не торкається) їх. Знайти рівняння асимптот можна двома способами, які допоможуть зрозуміти саму концепцію асимптот.

Метод1 З 2:

Розкладання на множники

Запишіть канонічне рівняння гіперболи.розглянемо найпростіший приклад-гіперболу, центр якої розташований на початку координат. У цьому випадку канонічне рівняння гіперболи має вигляд: ^x²/_a² - ^y²/_b² = 1 (коли гілки гіперболи спрямовані вправо або вліво) або ^y²/_b² - ^x²/_a² = 1 (коли гілки гіперболи спрямовані вгору або вниз).^{[1]X
Джерело інформації} майте на увазі, що в цьому рівнянні «х» і «у» – це змінні, а «а» і «b» – постійні (тобто числа).
- Приклад 1:^{x ²} / ₉ - ^y² / ₁₆ = 1
- Деякі викладачі і автори підручників міняють місцями постійні «а» і «b».^{[2]X
  Джерело інформації} тому вивчіть дане вам рівняння, щоб зрозуміти, що до чого. Не варто просто запам'ятовувати рівняння-в цьому випадку ви нічого не зрозумієте, якщо змінні і/або постійні будуть позначені іншими символами.
Прирівняйте канонічне рівняння до нуля (а не до одиниці).нове рівняння описує обидві асимптоти, але щоб отримати рівняння кожної асимптоти, доведеться докласти деяких зусиль.^{[3]X
Джерело інформації}
- Приклад 1:^{x ²} / ₉ - ^y² / ₁₆ = 0
Розкладіть на множники нове рівняння.розкладіть на множники ліву частину рівняння. Згадайте, як розкладати на множники квадратне рівняння, і читайте далі.
- Кінцеве рівняння (тобто рівняння, розкладене на множники) матиме вигляд(__ ± __)(__ ± __) = 0.
- При перемноженні перших членів (всередині кожної пари дужок) повинен вийти член^x²/₉, тому з цього члена витягніть квадратний корінь, і результат запишіть замість першого пробілу всередині кожної пари дужок:(^x/₃ ± __)(^x/₃ ± __) = 0
- Аналогічно витягніть квадратний корінь з члена^y²/₁₆, і результат запишіть замість другого пробілу всередині кожної пари дужок: (^x/₃ ± ^y/₄)(^x/₃ ± ^y/₄) = 0
- Ви знайшли всі члени рівняння, тому всередині однієї пари дужок між членами напишіть знак плюс, а всередині другої – знак мінус, щоб при перемноженні відповідні члени скорочувалися:(^x/₃ + ^y/₄)(^x/₃ - ^y/₄) = 0
Прирівняйте кожен двучлен (тобто вираз всередині кожної пари дужок) до нуля і обчисліть «y».так ви знайдете два рівняння, які описують кожну асимптоту.
- Приклад 1: Так як (^x/₃ + ^y/₄)(^x/₃ - ^y/₄) = 0, то ^x/₃ + ^y/₄ = 0 і ^x/₃ - ^y/₄ = 0
- Перепишіть рівняння наступним чином:^x/₃ + ^y/₄ = 0 → ^y/₄ = - ^x/₃ → Y = -^4x/₃
- Перепишіть рівняння наступним чином:^x/₃ - ^y/₄ = 0 → - ^y/₄ = - ^x/₃ → Y =^4x/₃
Виконайте описані дії з гіперболою, рівняння якої відрізняється від канонічного. у попередньому кроці ви знайшли рівняння асимптот гіперболи з центром на початку координат. Якщо Центр гіперболи знаходиться в точці з координатами (h,k), то вона описується наступним рівнянням: ^{(x - h)²}/_a² - ^{(y - k)²}/_b² = 1 або ^{(y - k)²}/_B² - ^{(x - h)²}/_a² = 1. Це рівняння також можна розкласти на множники. Але в цьому випадку не чіпайте двучлени (x-h) і (y-k) до тих пір, поки не прийдете до останнього кроку.
- Приклад 2:^{(x - 3)²}/₄ - ^{(y + 1)²}/₂₅ = 1
- Прирівняйте це рівняння до 0 і розкладіть його на множники:
- (^{(x - 3)}/₂ + ^{(y + 1)}/₅)(^{(x - 3)}/₂ - ^{(y + 1)}/₅) = 0
- Прирівняйте кожен двучлен (тобто вираз всередині кожної пари дужок) до нуля і обчисліть «y», щоб знайти рівняння асимптот:
- ^{(x - 3)}/₂ + ^{(y + 1)}/₅ = 0 → Y = -⁵/₂x + ¹³/₂
- (^{(x - 3)}/₂ - ^{(y + 1)}/₅) = 0 → Y =⁵/₂x - ¹⁷/₂

Метод2 З 2:

Обчислення y

Відокремте член y² на лівій стороні рівняння гіперболи.застосовуйте цей метод в тому випадку, коли рівняння гіперболи дано в квадратичній формі. Навіть якщо дано канонічне рівняння гіперболи, цей метод дозволить краще зрозуміти концепцію асимптот. Відокремте y² або (y - k)² на лівій стороні рівняння.
- Приклад 3:^{(y + 2)²}/₁₆ - ^{(x + 3)²}/₄ = 1
- До обох частин рівняння додайте "х", а потім помножте обидві частини на 16:
- (y + 2)² = 16(1 + ^{(x + 3)²}/₄)
- Спростіть отримане рівняння:
- (y + 2)² = 16 + 4(x + 3)²
Витягніть квадратний корінь з кожної частини рівняння.при цьому не спрощуйте праву частину рівняння, так як при добуванні квадратного кореня виходять два результати – позитивний і негативний (наприклад, -2 * -2 = 4, тому √4 = 2 і √4 = -2). Щоб привести обидва результати, використовуйте символ ±.
- √((y + 2)²) = √(16 + 4(x + 3)²)
- (y+2) = ± √(16 + 4(x + 3)²)
Зрозумійте поняття асимптоти.зробіть це, перш ніж перейти до наступного кроку. Асимптота-це пряма, до якої наближається гіпербола з ростом значень «х». Гіпербола ніколи не перетне асимптоту, але зі збільшенням «х» гіпербола наблизиться до асимптоти на нескінченно малу відстань.
Перетворіть рівняння з урахуванням великих значень «х».як правило, при роботі з рівняннями асимптот враховуються тільки великі значення " х " (тобто такі значення, які прагнуть до нескінченності). Тому в рівнянні можна знехтувати певними константами, так як в порівнянні з «х» їх внесок невеликий. Наприклад, якщо змінна «х» дорівнює кільком мільярдам, то додаток числа (константи) 3 матиме мізерний вплив на значення «х».
- У рівнянні(y+2) = ± √(16 + 4(x + 3)²) при прагненні «x» до нескінченності постійної 16 можна знехтувати.
- При великих значеннях " х "(y+2) ≈ ± √(4(x + 3)²)
Обчисліть "у", щоб знайти рівняння асимптот.позбувшись від констант, можна спростити підкорене вираз. Пам'ятайте, що у відповіді потрібно записати два рівняння – одне зі знаком плюс, а друге зі знаком мінус.
- Y + 2 = ±√(4(x+3)^2)
- Y + 2 = ±2(x+3)
- Y + 2 = 2x + 6і y + 2 = - 2x-6
- Y = 2x + 4 і Y = - 2x-8

Поради

Пам'ятайте, що рівняння гіперболи і рівняння її асимптот завжди включають постійні (константи).
Рівностороння гіпербола - це гіпербола, в рівнянні якої а = b = с (константа).
Якщо дано рівняння рівносторонньої гіперболи, спочатку перетворіть його в канонічну форму, а потім знайдіть рівняння асимптот.