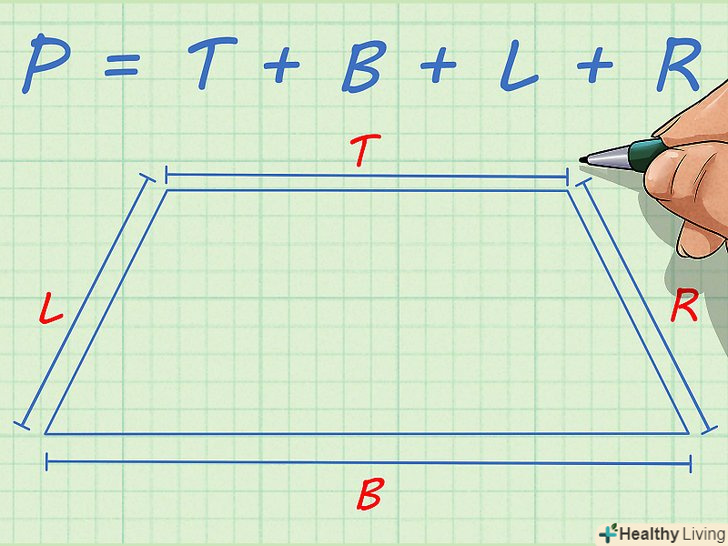
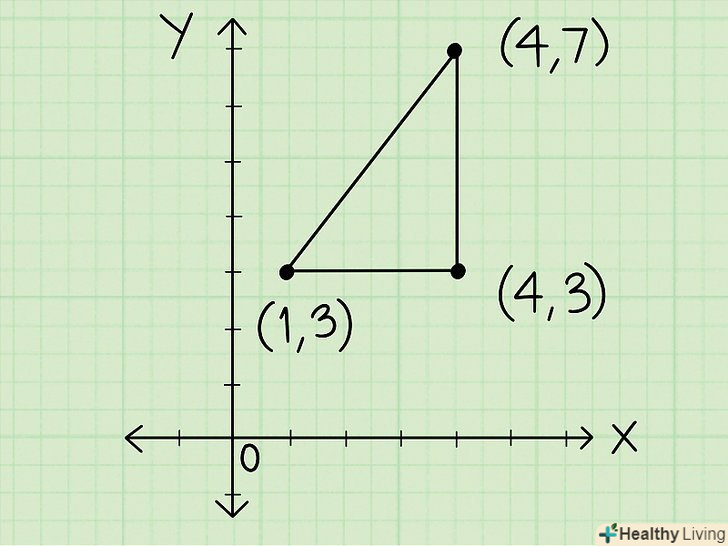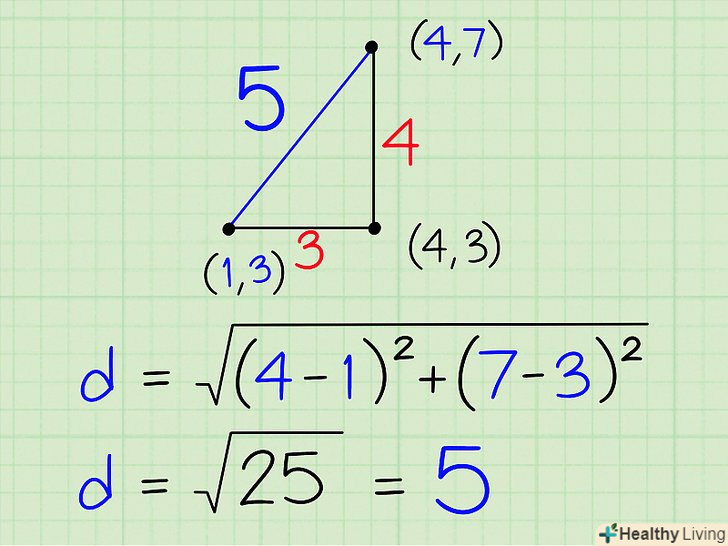1. Головна
    2. Геометрія
    3. Як знайти периметр багатокутника-

Як знайти периметр багатокутника-

Багатокутник-це двовимірна фігура, яка обмежена замкнутою ламаною лінією (без самопересічень). Існують правильні багатокутники, всі сторони яких рівні, і неправильні багатокутники, довжини сторін яких різні. Процеси обчислення периметрів правильного і неправильного багатокутників трохи різняться, але вони прості, якщо знати, що робити. Також периметри правильних і неправильних багатокутників можна знайти, якщо фігури побудувати на площині координат. Периметр правильного багатокутника можна обчислити за формулою: периметр = кількість сторін x довжина будь-якої сторони.

Метод1З 3:
Як обчислити периметр правильного багатокутника

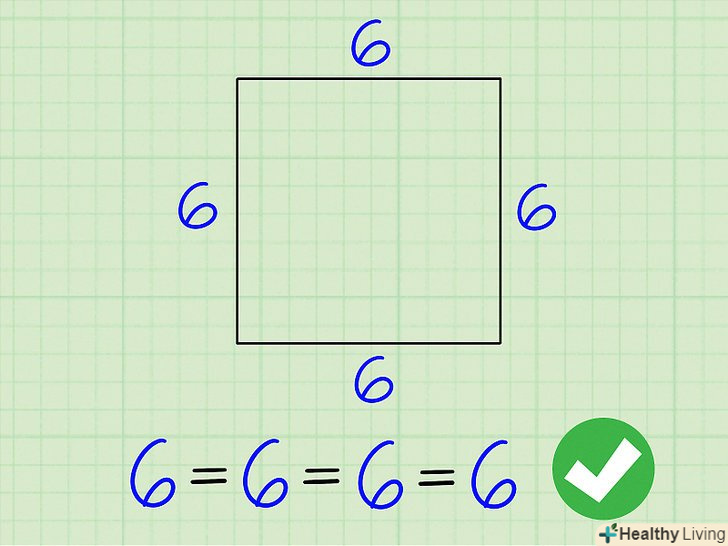
  1. Переконайтеся, що сторони багатокутника рівні. правильний багатокутник-це багатокутник з рівними сторонами. Якщо сторони багатокутника не рівні, скористайтеся методом обчислення периметра неправильного багатокутника.[1]

    Якщо довжини всіх сторін не дані, зверніть увагу на форму багатокутника, щоб спробувати визначити їх. Наприклад, якщо дано квадрат з однією відомою стороною, інші сторони будуть тієї ж довжини, тому що сторони квадрата рівні.

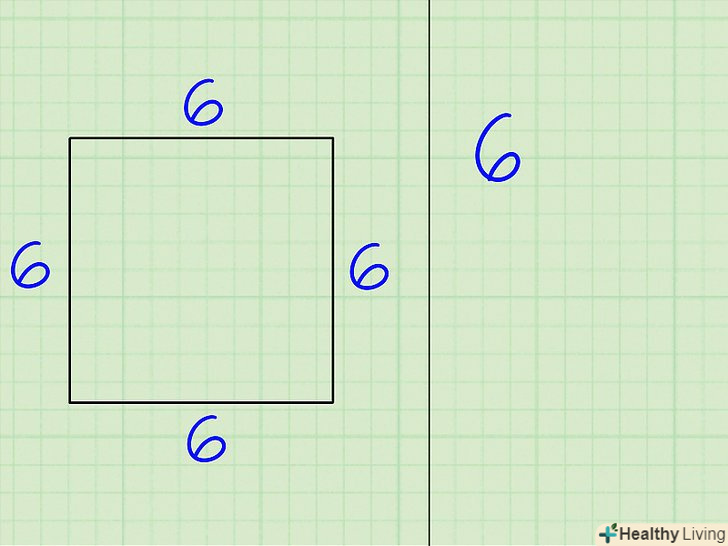
  2. Запишіть значення однієї сторони багатокутника. Виберіть будь-яку сторону, так як в правильному багатокутнику всі сторони рівні. Просто переконайтеся, що записуєте значення тільки однієї сторони.[2]
    • Наприклад, якщо дано квадрат зі стороною 6 см, запишіть " 6 см».
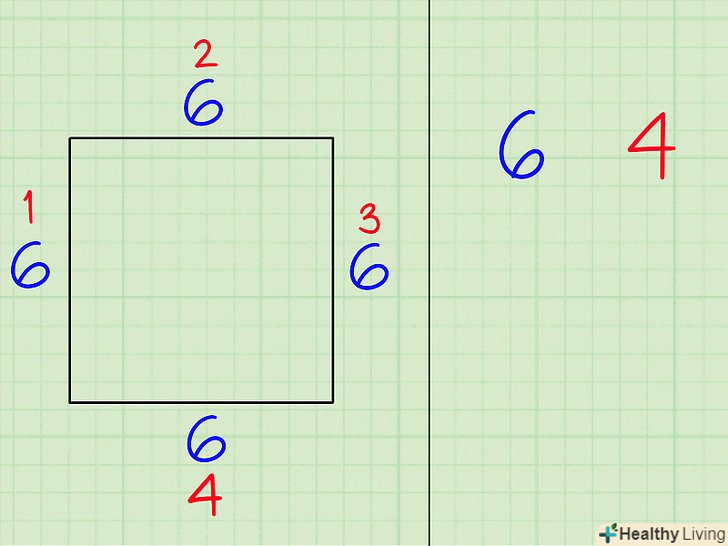
  3. Запишіть кількість сторін багатокутника.не думайте про довжини інших сторін - просто підрахуйте, скільки сторін у багатокутника, і запишіть це число.[3]
    • У випадку квадрата запишіть "4", так як у квадрата 4 сторони.
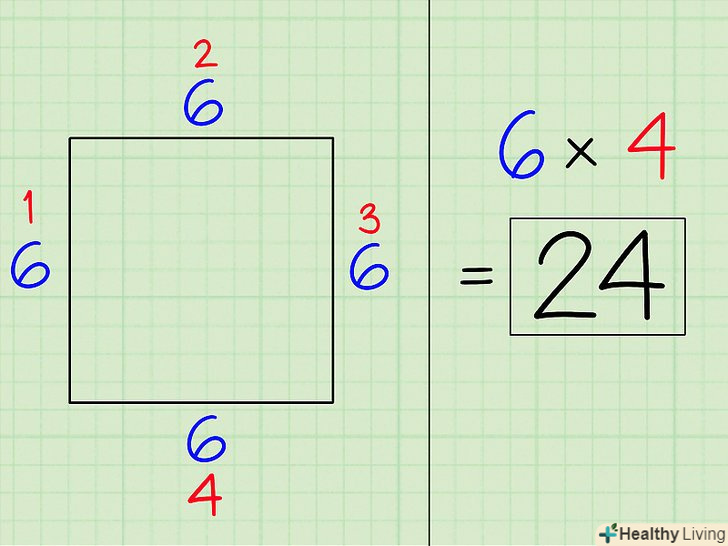
  4. Перемножте значення сторони на кількість сторін, щоб обчислити периметр. Формула для знаходження периметра правильного багатокутника: периметр = кількість сторін x довжину будь-якої сторони.[4]
    • У нашому прикладі значення сторони квадрата 6 см і у квадрата 4 сторони. Тому 6 х 4 = 24 см — це периметр квадрата.
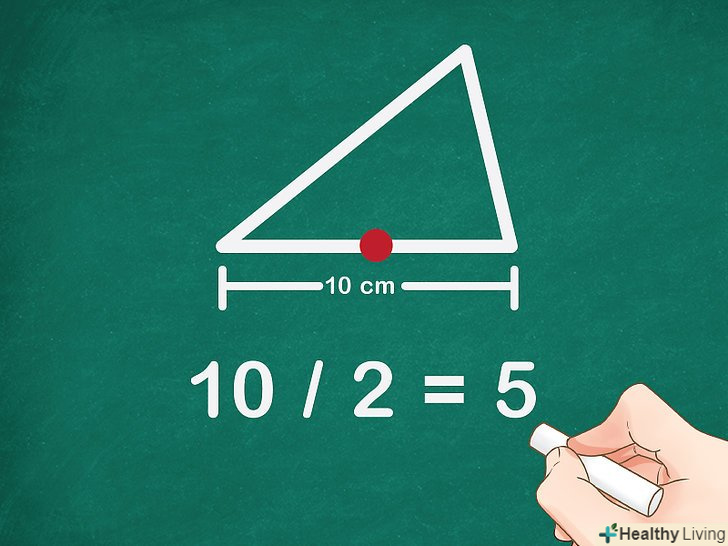
    • Інший приклад: дано трикутник з бічною довжиною 3 см.у трикутника 3 сторони, тому 3 х 3 = 9 см — це периметр трикутника.

Метод2 З 3:
Як обчислити периметр неправильного багатокутника

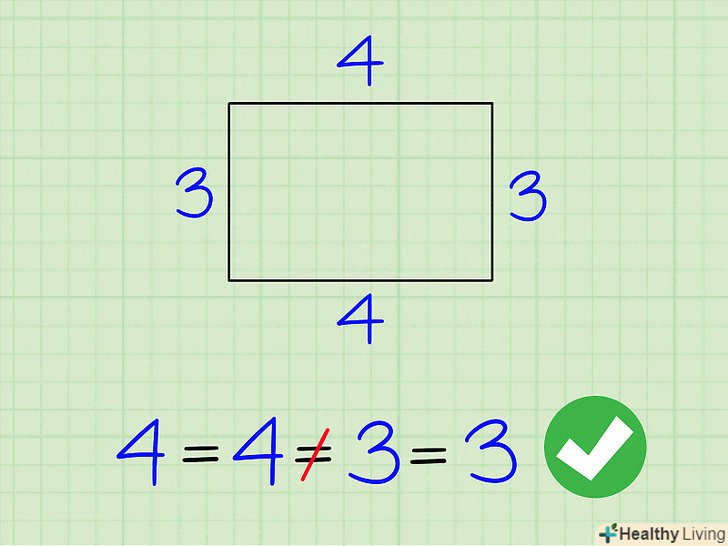
  1. Подивіться на довжини сторін багатокутника, щоб визначити, чи є він неправильним.у неправильного багатокутника сторони не рівні (багатокутник з рівними сторонами називається правильним).[5]

    Запам'ятайте: метод для обчислення периметра неправильного багатокутника можна застосовувати до правильних багатокутників, але не навпаки.

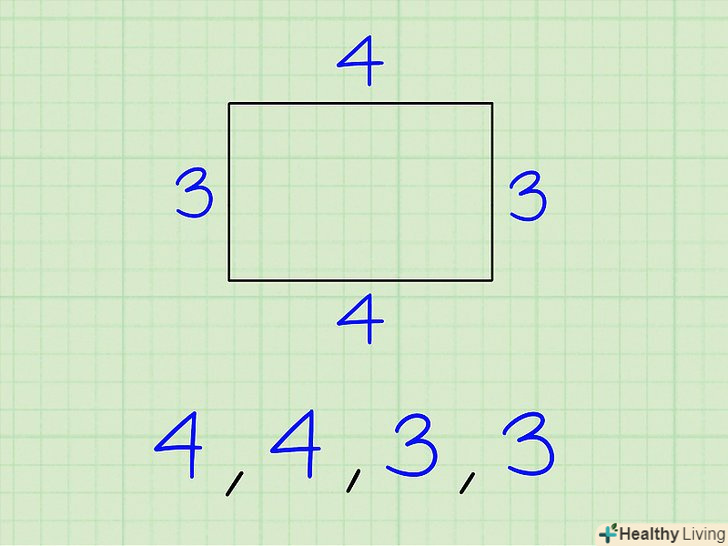
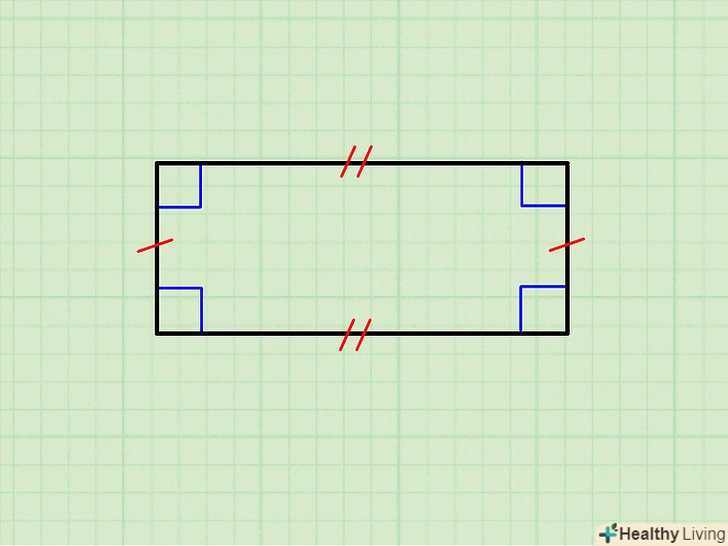
  2. Запишіть значення кожної сторони багатокутника.зробіть це, оскільки у неправильного багатокутника сторони різні. Навіть якщо деякі з сторін рівні, все одно запишіть довжину кожної сторони.[6]
    • Наприклад, якщо дано прямокутник, дві сторони якого рівні 4 см, а інші дві 3 см, запишіть «4 см, 4 см, 3 см, 3 см».
    • Якщо дано неправильний багатокутник, одна сторона якого дорівнює 2 см, друга дорівнює 3 см, третя дорівнює 4 см, запишіть «2 см, 3 см, 4 см».
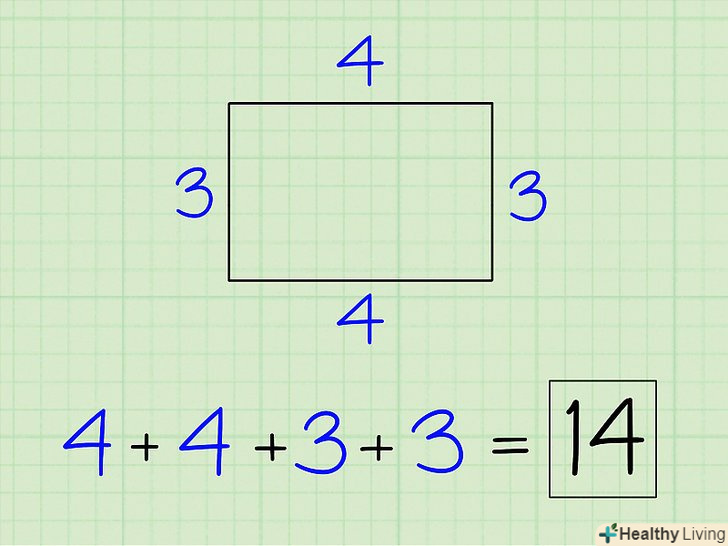
  3. Складіть значення всіх сторін, щоб знайти периметр неправильного багатокутника. просто складіть всі значення, які ви записали, і отримаєте периметр багатокутника.[7]
    • У нашому прикладі з прямокутником: 4 + 4 + 3 + 3 = 14 см-це периметр багатокутника.

Метод3 З 3:
Як обчислити периметр багатокутника за заданими координатами

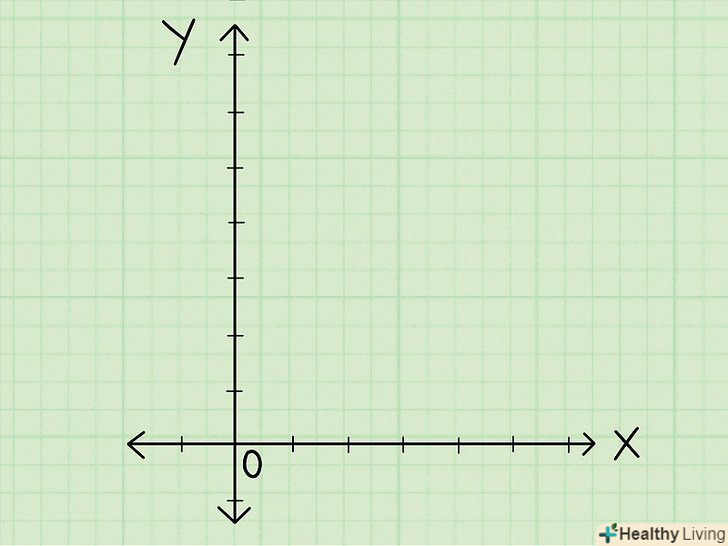
  1. Намалюйте площину координат з осями X і Y. на площину координат потрібно нанести точки із заданими координатами. Щоб намалювати площину координат, візьміть папір в клітку або за допомогою лінійки намалюйте сітку на чистому аркуші паперу. Тепер намалюйте горизонтальну пряму (вісь Х) і перпендикулярно їй посередині проведіть вертикальну пряму (вісь Y). Точку перетину двох прямих позначте як "0".[8]
    • Коли будете наносити координатні мітки, цифри над і справа "0 «будуть позитивними, а цифри під і зліва» 0" будуть негативними.
  2. Нанесіть точки з заданими координатамиНа координатну площину.у задачі будуть дані координати всіх вершин багатокутника, периметр якого потрібно знайти. Кожна пара координат записується так: (1,2). Використовуйте координатні мітки, щоб нанести точки на площину координат. Коли ви нанесете всі точки, з'єднайте їх прямими лініями, щоб побудувати багатокутник.[9]

    Запам'ятайте: перше число в парі координат (координата «х») відкладається по осі Х, а друге число (координата «y») — по осі Y. наприклад, щоб нанести точку з координатами (2,4), відрахуйте 2 мітки по осі Х і 4 мітки по осі Y, а потім відзначте точку перетину.

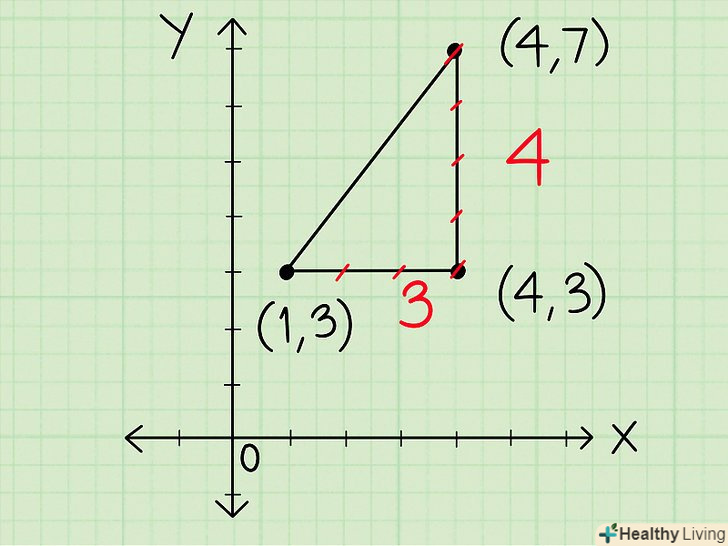
  3. Знайдіть значення вертикальних і горизонтальних сторін.необхідно знати довжину кожної сторони багатокутника, щоб визначити її периметр. У разі вертикальної або горизонтальної сторони просто порахуйте число координатних міток між точками сторони. Потім запишіть число біля цієї сторони.[10]
    • Наприклад, щоб знайти довжину горизонтальної сторони, почніть з одного її кінця і порахуйте число координатних міток до іншого кінця сторони. Якщо ви нарахували 6 міток, Довжина цієї сторони становить 6 одиниць.
  4. Скористайтеся формулою для обчислення відстані, щоб знайти довжину похилих сторін.довжину похилої сторони не можна знайти, якщо просто порахувати координатні мітки між її кінцями. Тому скористайтеся формулою: D=(x2−x1)2+(y2−y1)2{\displaystyle d={\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}}. У формулу підставте значення координат "x» і" y " двох точок на кінцях сторони, довжину якої потрібно знайти.[11]
    • Наприклад, щоб знайти відстань (довжину сторони) між двома точками з координатами (4,7) і (1,3), підставте ці координати в формулу і отримаєте:D=(42−11)2+(72−31)2{\displaystyle d={\sqrt {(4_{2}-1_{1})^{2}+(7_{2}-3_{1})^{2}}}}
    • Спростіть рівняння та отримайте.
    • Обчисліть:D=25{\displaystyle d={\sqrt {25}}} = 5. Отже, довжина сторони дорівнює 5 одиниць.
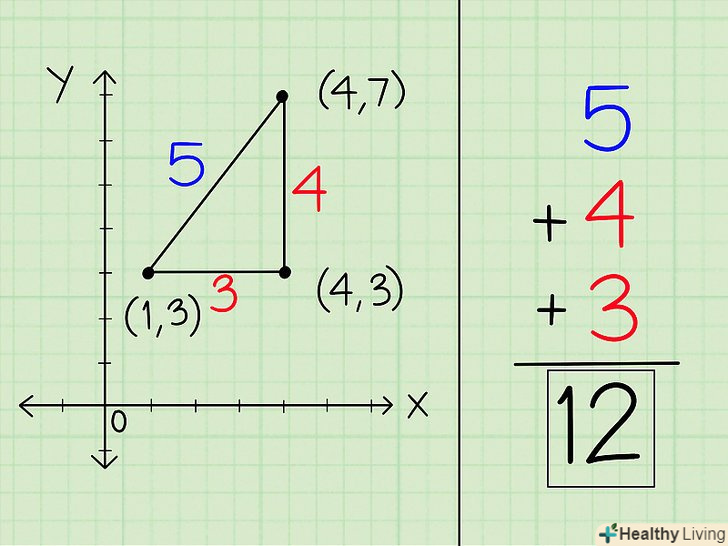
  5. Складіть довжини всіх сторін багатокутника, щоб знайти його периметр.Периметр багатокутника дорівнює сумі всіх його сторін. Коли ви обчислите значення кожної сторони багатокутника за даними координатам точок його вершин, просто складіть ці значення.
    • Наприклад, якщо на координатній площині ви побудували трикутник і вирахували, що його сторони рівні 3, 2 і 5, складіть ці числа, щоб отримати 10. Таким чином, периметр трикутника дорівнює 10 одиниць.

Джерела

  1. ↑ Https://www.mathopenref.com/polygonperimeter.html
  2. ↑ Https://www.mathopenref.com/polygonperimeter.html
  3. ↑ Https://www.mathopenref.com/polygonperimeter.html
  4. ↑ Https://www.mathopenref.com/polygonperimeter.html
  5. ↑ Https://www.mathopenref.com/polygonperimeter.html
  6. ↑ Https://www.mathopenref.com/polygonperimeter.html
  7. ↑ Https://www.mathopenref.com/polygonperimeter.html
  8. ↑ Https://www.algebra.com/algebra/homework/Polygons/Polygons.faq.question.881850.html
  9. ↑ Https://www.algebra.com/algebra/homework/Polygons/Polygons.faq.question.881850.html
  1. ↑ Https://www.algebra.com/algebra/homework/Polygons/Polygons.faq.question.881850.html
  2. ↑ Https://www.algebra.com/algebra/homework/Polygons/Polygons.faq.question.881850.html

Ще почитати: