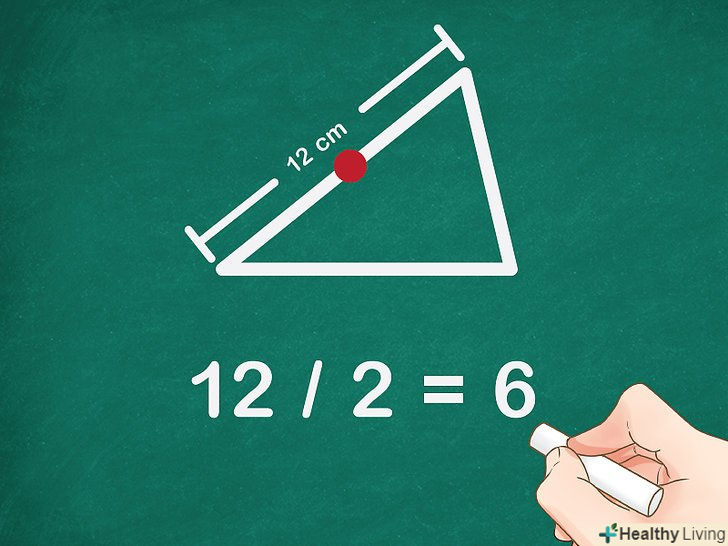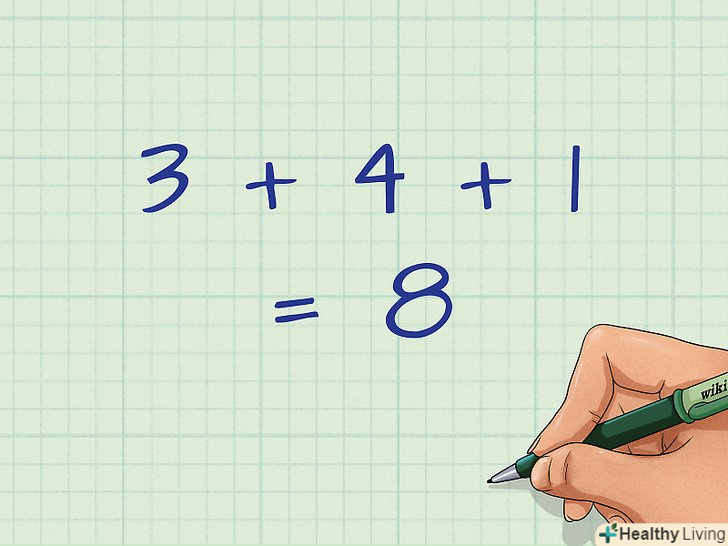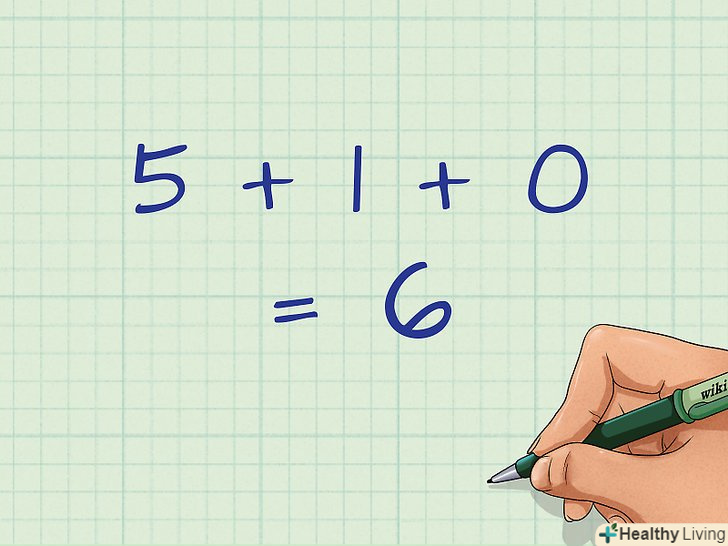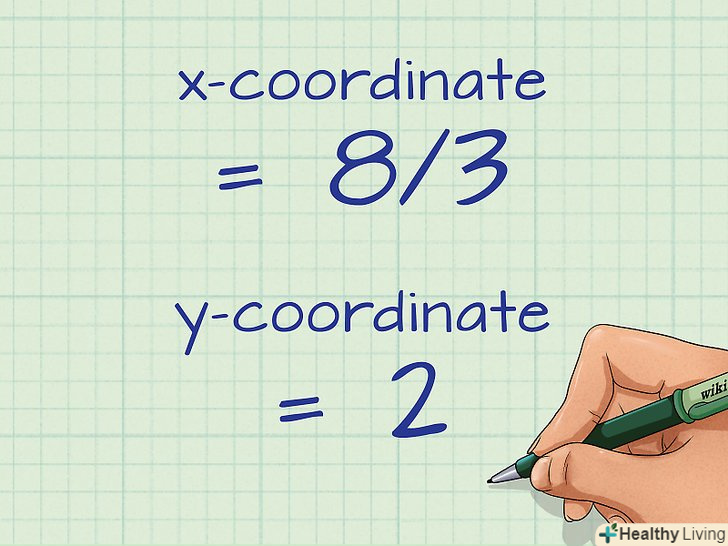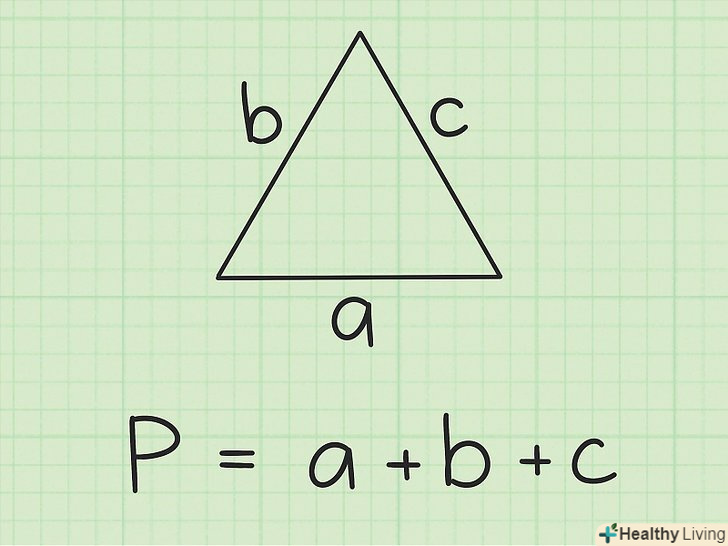Центр ваги трикутника – Центроїд) - це точка центру мас. Уявіть собі трикутну лінійку, покладену на кінчик олівця. Лінійка буде балансувати, якщо кінчик олівця буде знаходитися в її центрі ваги. Розташування центроїда, яке легко знаходиться за допомогою геометрії, необхідно знати при роботі над дизайнерським або інженерним проектом.
Кроки
Метод1З 3:
Пересічні медіани
Метод1З 3:
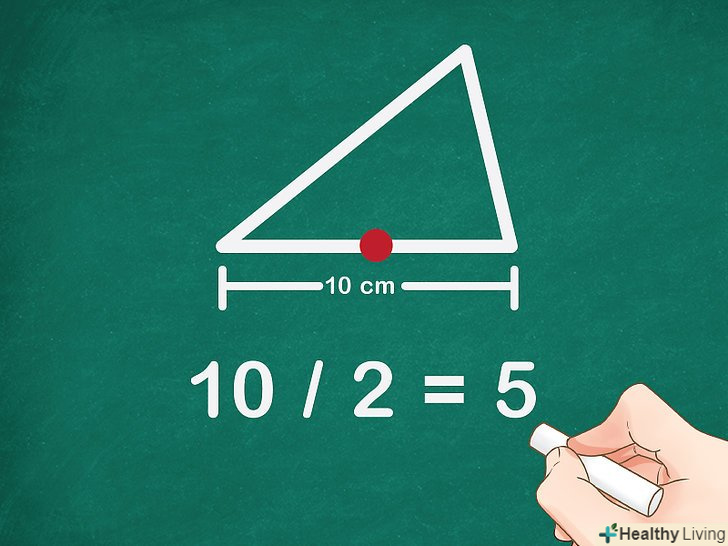
 Знайдіть середину однієї сторони трикутника.для цього виміряйте сторону і розділіть її довжину навпіл. Середину відзначте точкою A.
Знайдіть середину однієї сторони трикутника.для цього виміряйте сторону і розділіть її довжину навпіл. Середину відзначте точкою A.- Наприклад, якщо сторона трикутника дорівнює 10 см, то середина знаходиться на відстані 5 см (
) від вершини трикутника.
- Наприклад, якщо сторона трикутника дорівнює 10 см, то середина знаходиться на відстані 5 см (
 Знайдіть середину другої сторони трикутника.для цього виміряйте сторону і розділіть її довжину навпіл. Середину відзначте точкою в.
Знайдіть середину другої сторони трикутника.для цього виміряйте сторону і розділіть її довжину навпіл. Середину відзначте точкою в.- Наприклад, якщо друга сторона трикутника дорівнює 12 см, то середина знаходиться на відстані 6 см (
) від вершини трикутника.
- Наприклад, якщо друга сторона трикутника дорівнює 12 см, то середина знаходиться на відстані 6 см (
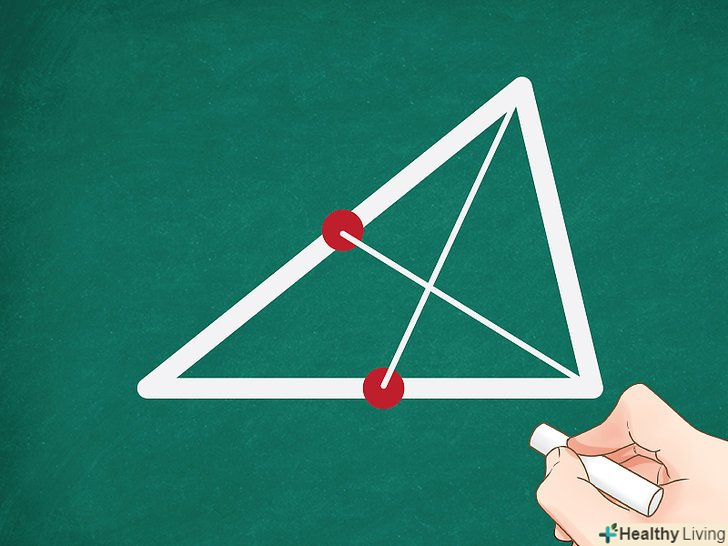
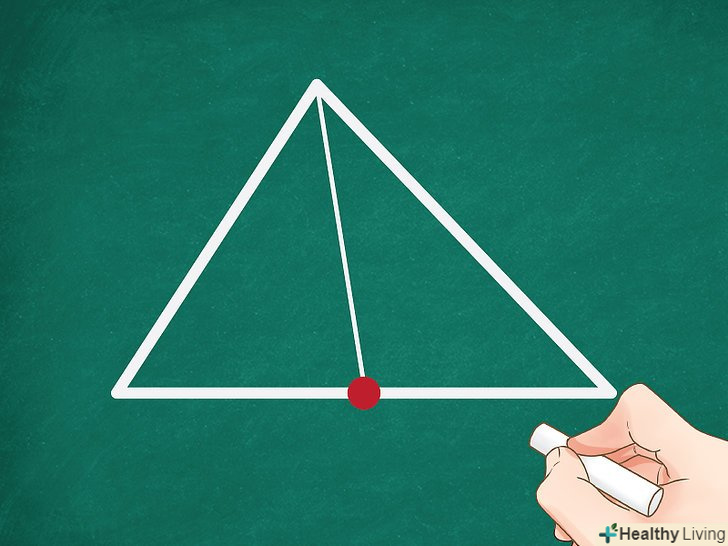
 З'єднайте середини сторін з протилежними вершинами. Ви отримаєте дві медіани.[1]
З'єднайте середини сторін з протилежними вершинами. Ви отримаєте дві медіани.[1]- Вершина-це точка, в якій сходяться дві сторони трикутника.

Метод2 З 3:
Відношення 2:1
Метод2 З 3:
 Проведіть медіану. медіана-це відрізок, який з'єднує вершину трикутника з серединою протилежної сторони. Можна працювати з будь медіаною.
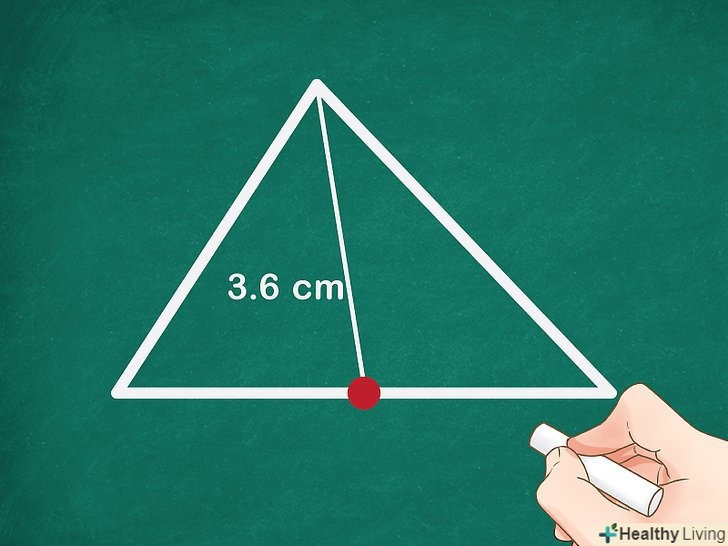
Проведіть медіану. медіана-це відрізок, який з'єднує вершину трикутника з серединою протилежної сторони. Можна працювати з будь медіаною. Виміряйте довжину медіани.зробіть це акуратно і точно.
Виміряйте довжину медіани.зробіть це акуратно і точно.- Наприклад, медіана дорівнює 3,6 см.
 Знайдіть третю частину (третину) медіани.для цього розділіть довжину медіани на три. Зробіть це акуратно і точно. Округливши отримане значення, ви не знайдете Центроїд.
Знайдіть третю частину (третину) медіани.для цього розділіть довжину медіани на три. Зробіть це акуратно і точно. Округливши отримане значення, ви не знайдете Центроїд.- У нашому прикладі медіана дорівнює 3,6 см. Тому розділіть 3,6 на 3:
. Таким чином, третина медіани дорівнює 1,2 см.
- У нашому прикладі медіана дорівнює 3,6 см. Тому розділіть 3,6 на 3:
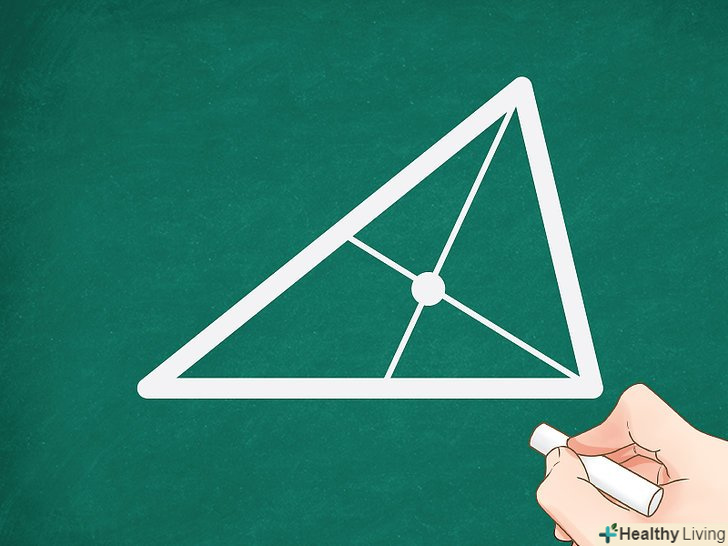
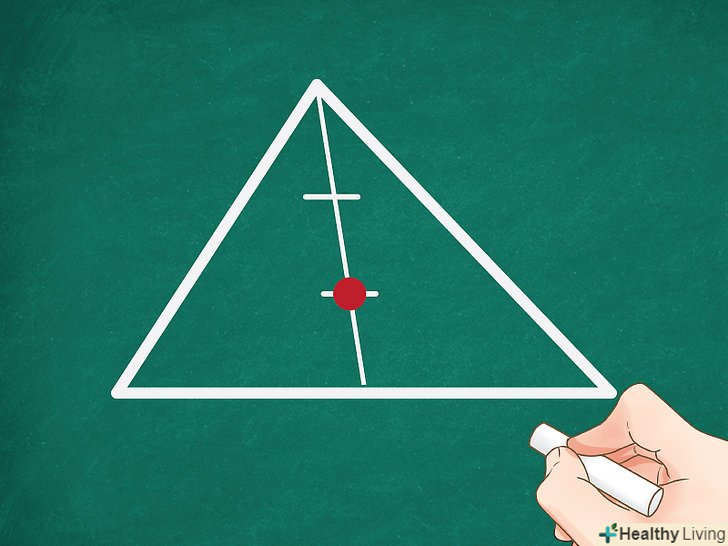
 Третину медіани відзначте крапкою. ця точка є центроїдом, тому що він завжди ділить медіану трикутника відносно 2:1. Тобто центр ваги знаходиться на відстані, яке дорівнює ⅓ довжини медіани, від середини сторони, або на відстані, яке дорівнює ⅔ довжини медіани, від вершини трикутника.[4]
Третину медіани відзначте крапкою. ця точка є центроїдом, тому що він завжди ділить медіану трикутника відносно 2:1. Тобто центр ваги знаходиться на відстані, яке дорівнює ⅓ довжини медіани, від середини сторони, або на відстані, яке дорівнює ⅔ довжини медіани, від вершини трикутника.[4]- Наприклад, якщо медіана дорівнює 3,6 см, то Центроїд знаходиться на відстані 1,2 см від середини сторони.
Метод3 З 3:
Усереднені координати
Метод3 З 3:
 Визначте координати трьох вершин трикутника.координати можуть бути дані; в іншому випадку буде дано трикутник, побудований на координатній площині. Координати подаються у вигляді
Визначте координати трьох вершин трикутника.координати можуть бути дані; в іншому випадку буде дано трикутник, побудований на координатній площині. Координати подаються у вигляді.
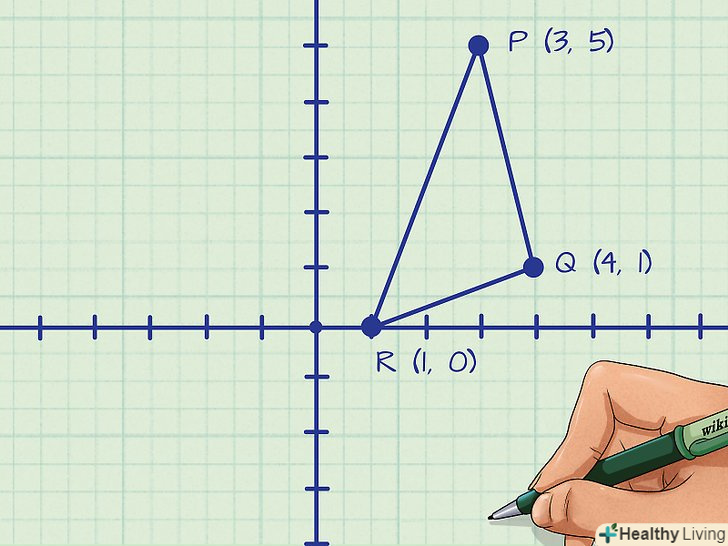
- Наприклад, дано трикутник PQR, вершини якого мають наступні координати: P (3,5), Q (4,1), R (1,0).
 Складіть значення координат "х".не забудьте скласти всі три значення. Ви не знайдете центр ваги, якщо будете працювати тільки з двома значеннями.
Складіть значення координат "х".не забудьте скласти всі три значення. Ви не знайдете центр ваги, якщо будете працювати тільки з двома значеннями.- Наприклад, якщо координати» х "дорівнюють 3, 4 і 1, складіть ці значення:
.
- Наприклад, якщо координати» х "дорівнюють 3, 4 і 1, складіть ці значення:
 Складіть значення координат»у".не забудьте скласти всі три значення.
Складіть значення координат»у".не забудьте скласти всі три значення.- Наприклад, якщо координати» у "дорівнюють 5, 1 і 0, складіть ці значення:
.
- Наприклад, якщо координати» у "дорівнюють 5, 1 і 0, складіть ці значення:
 Знайдіть середні значення сум координат «х» і «у».отримані значення будуть відповідати центру тяжіння трикутника.[5] щоб знайти середнє значення, розділіть кожну суму на 3.
Знайдіть середні значення сум координат «х» і «у».отримані значення будуть відповідати центру тяжіння трикутника.[5] щоб знайти середнє значення, розділіть кожну суму на 3.- Наприклад, якщо сума координат «х» дорівнює 8, то середнє значення дорівнює
. Якщо сума координат» у "дорівнює 6, то середнє значення дорівнює
=
- Наприклад, якщо сума координат «х» дорівнює 8, то середнє значення дорівнює
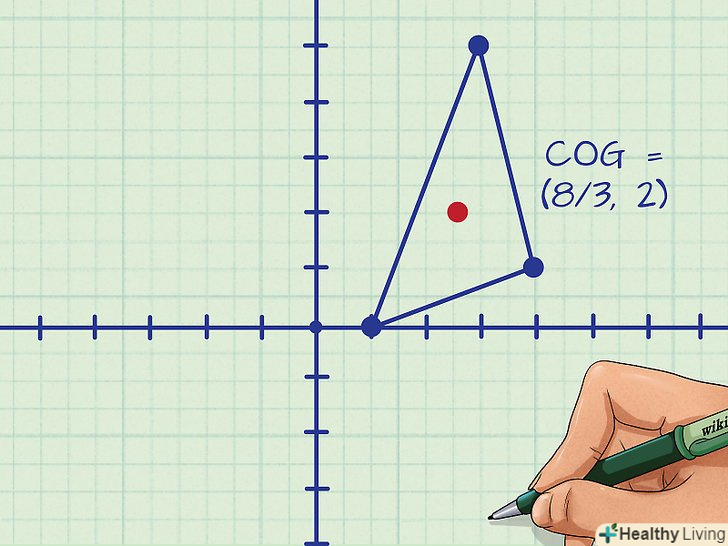
 Нанесіть точку центру тяжіння на трикутник. Центр ваги знаходиться в точці, координати якої рівні середнім значенням Сум координат "х»і "у".
Нанесіть точку центру тяжіння на трикутник. Центр ваги знаходиться в точці, координати якої рівні середнім значенням Сум координат "х»і "у".- У нашому прикладі центр ваги – це точка з координатами
.
- У нашому прикладі центр ваги – це точка з координатами
Поради
- Не має значення, з якою стороною трикутника ви працюєте – центр ваги буде знаходиться в одній і тій же точці. Якщо побудувати медіани для всіх трьох сторін, вони перетнуться в одній точці.
Джерела
- ↑ Http://jwilson.coe.uga.edu/EMAT6680Fa06/Chitsonga/MEDIAN/THE%20MEDIANS%20OF%20A%20TRIANGLE.htm
- ↑ Http://jwilson.coe.uga.edu/emat6680su09/park/As4dspark/As4dspark.html
- ↑ Https://www.mathsisfun.com/geometry/triangle-centers.html
- ↑ Http://jwilson.coe.uga.edu/emat6680su09/park/As4dspark/As4dspark.html
- ↑ Https://www.khanacademy.org/math/geometry/triangle-properties/medians-centroids/v/triangle-medians-and-centroids